14.1全等三角形- 沪科版数学八年级上册课件(18张)
文档属性
| 名称 | 14.1全等三角形- 沪科版数学八年级上册课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 166.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 10:15:28 | ||
图片预览


文档简介
(共18张PPT)
《14.1全等三角形》
A
B
C
D
E
F
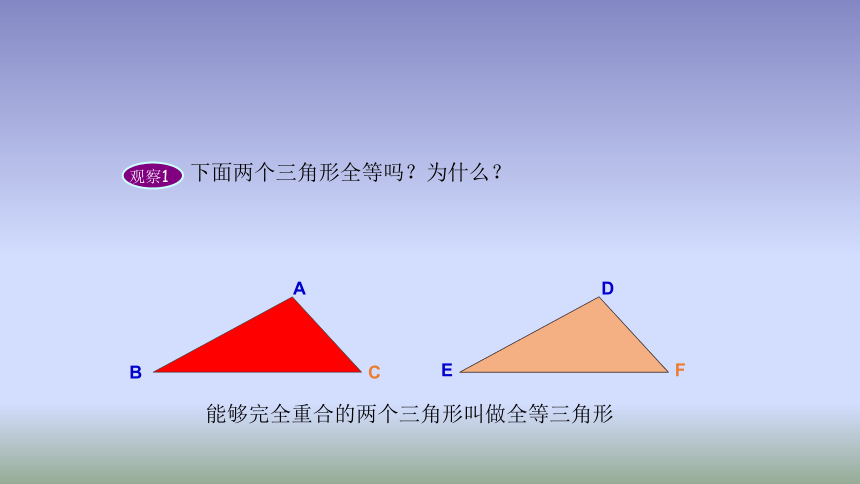
观察1
下面两个三角形全等吗?为什么?
能够完全重合的两个三角形叫做全等三角形
探究新知
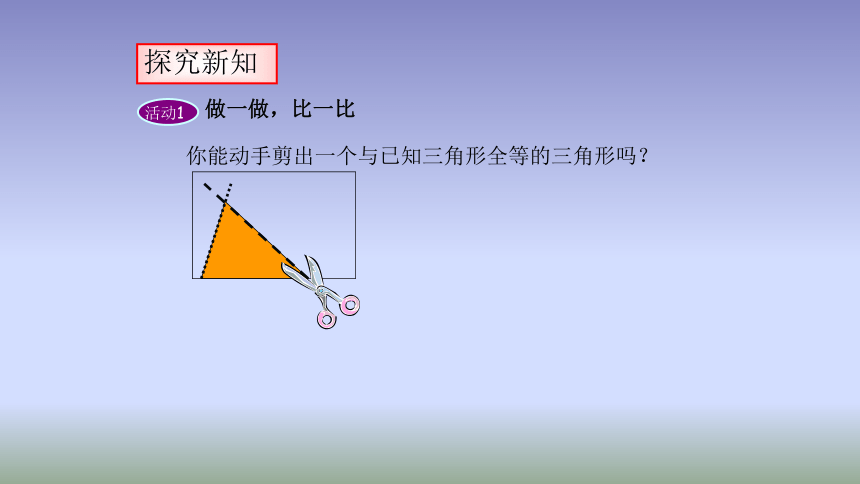
活动1
你能动手剪出一个与已知三角形全等的三角形吗?
做一做,比一比
∴A
B=D
E,A
C=D
F,BC=
E
F
∠A=∠D,∠B=∠E,∠C=∠F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
∵?ABC≌
?DEF
全等三角形的性质:对应边相等,对应角相等。
活动2
拿出同学们刚才剪出的两个全等三角形,如果任意摆放能重合吗?该怎样摆放它们才能重合呢?由三角形重合你能发现什么结论?同学们小组讨论、交流,归纳得出结论。
几何语言:
对应边
对应角
A
B
C
D
E
F
A
B
C
D
E
F
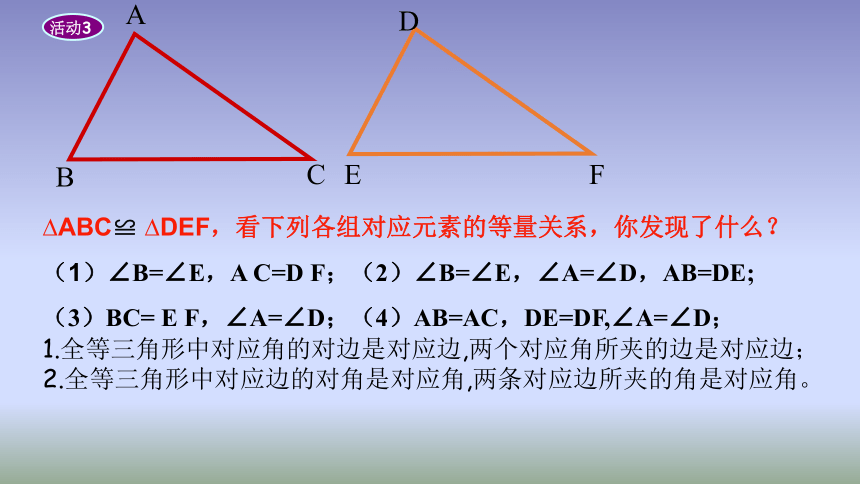
?ABC≌
?DEF,看下列各组对应元素的等量关系,你发现了什么?
(1)∠B=∠E,A
C=D
F;(2)∠B=∠E,∠A=∠D,AB=DE;
(3)BC=
E
F,∠A=∠D;(4)AB=AC,DE=DF,∠A=∠D;
1.全等三角形中对应角的对边是对应边,两个对应角所夹的边是对应边;
2.全等三角形中对应边的对角是对应角,两条对应边所夹的角是对应角。
活动3
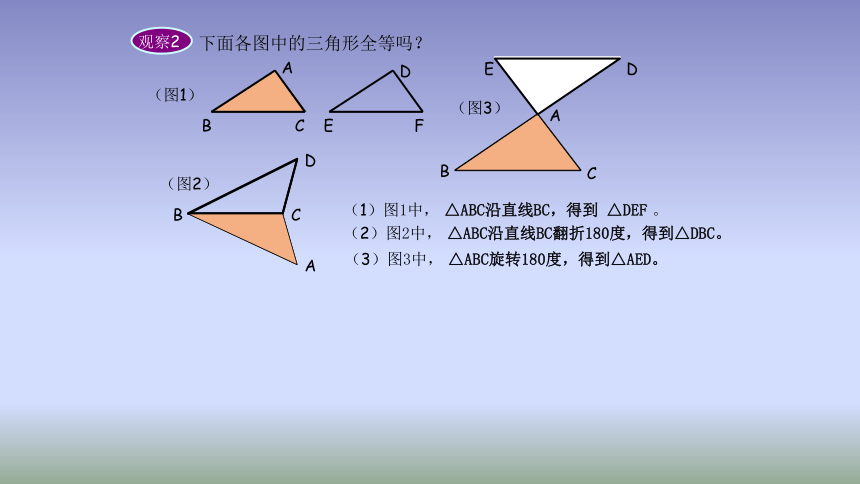
观察2
下面各图中的三角形全等吗?
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
(图1)
(图2)
(图3)
(1)图1中,
△ABC沿直线BC,得到
△DEF
。
(2)图2中,
△ABC沿直线BC翻折180度,得到△DBC。
(3)图3中,
△ABC旋转180度,得到△AED。
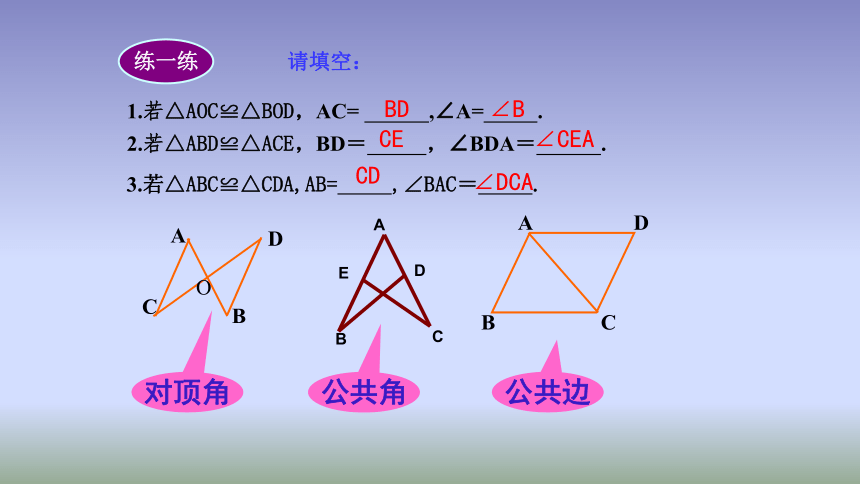
1.若△AOC≌△BOD,AC=
,∠A=
.
A
B
O
C
D
2.若△ABD≌△ACE,BD=
,∠BDA=
.
3.若△ABC≌△CDA,AB=
,∠BAC=
.
A
B
C
D
请填空:
A
B
C
D
E
对顶角
公共角
公共边
练一练
∠B
BD
CE
∠CEA
CD
∠DCA
试一试
讨论总结:根据以上图形,归纳找全等三角形对应元素的方法。
试一试
a.全等三角形中对应角的对边是对应边,两个对应角所夹的边是对应边;
b.全等三角形中对应边的对角是对应角,两条对应边所夹的角是对应角;
c.有公共边的,公共边一定是对应边;
d.有公共角的,公共角一定是对应角;
e.有对顶角的,对顶角一定是对应角;
f.一对最长的边是对应边,一对最短的边是对应边;一对最大的角是对应角,一对最小的角是对应角。
讨论总结:根据以上图形,归纳找全等三角形对应元素的方法。
1.全等形中可以不同的是(
)
A.图形的位置 B.图形的形状
C.图形的周长
D.图形的面积
A
[归纳]
(1)全等形:能够____________的两个图形,叫做全等形.
(2)判定两个图形全等的方法:两个图形只要满足_________相同,并且_________相等,它们就是全等形;平移、旋转、翻折前后的图形全等.
完全重合
形状
大小
小试牛刀
2.如右图,已知△ABC≌△DEC,B和E,A和D是对应顶点,说出这两个三角形中对应的边和角。
3.如右图,已知△ABD≌△ACE,
且∠C=45°,AC
=
5,AE
=
3,则
∠B
=
,
DC
=
.
A
E
B
C
D
2
45°
D
B
E
A
C
如图,△ABC≌△DEC,CA和CD,CB和CE是对应边,
∠
ACD和∠BCE相等吗?为什么?
D
B
E
A
C
解:∠
ACD=∠BCE
理由:
∵
△ABC≌△DEC,
∴
∠
DCE
=∠ACB,
又∵
∠
ACD
=
∠
DCE
-
∠
1,
∠BCE
=
∠ACB
-
∠
1,
∴
∠
ACD
=
∠BCE.
1
思考提升
课堂小结
1.全等形、全等三角形的概念;
2.全等三角形的性质;
3.全等三角形的表示方法;
4.全等三角形中的对应关系。
这节课你学会了什么?有哪些收获?有什么感受?请把你的想法告诉你的同桌,然后告诉老师。
试一试
归纳:找全等三角形中对应元素的方法。
A
B
C
D
E
F
?ABC≌
?DEF,看下列各组对应元素的等量关系,你发现了什么?
(1)∠B=∠E,A
C=D
F;(2)∠B=∠E,∠A=∠D,AB=DE;
(3)BC=
E
F,∠A=∠D;(4)AB=AC,DE=DF,∠A=∠D;
1.全等三角形中对应角的对边是对应边,两个对应角所夹的边是对应边;
2.全等三角形中对应边的对角是对应角,两条对应边所夹的角是对应角;
活动3
观察下面的图形变换,找出全等三角形,并指出对应边和对应角。
A
B
C
D
A
B
C
D
O
A
B
C
D
E
3.有公共边的,公共边一定是对应边;
4.有公共角的,公共角一定是对应角;
5.有对顶角的,对顶角一定是对应角;
观察
C
A
B
F
E
D
对应边是:
对应角是:
AC与DF,AB与DE,BC与EF
∠A与∠D,∠B与∠E,∠C与∠F
6.一对最长的边是对应边,一对最短的边是对应边;
一对最大的角是对应角,一对最小的角是对应角;
1.全等三角形中对应角的对边是对应边,两个对应角所夹的边是对应边;
2.全等三角形中对应边的对角是对应角,两条对应边所夹的角是对应角;
3.有公共边的,公共边一定是对应边;
4.有公共角的,公共角一定是对应角;
5.有对顶角的,对顶角一定是对应角;
6.一对最长的边是对应边,一对最短的边是对应边;一对最大的角是对应角,一对最小的角是对应角。
《14.1全等三角形》
A
B
C
D
E
F
观察1
下面两个三角形全等吗?为什么?
能够完全重合的两个三角形叫做全等三角形
探究新知
活动1
你能动手剪出一个与已知三角形全等的三角形吗?
做一做,比一比
∴A
B=D
E,A
C=D
F,BC=
E
F
∠A=∠D,∠B=∠E,∠C=∠F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
∵?ABC≌
?DEF
全等三角形的性质:对应边相等,对应角相等。
活动2
拿出同学们刚才剪出的两个全等三角形,如果任意摆放能重合吗?该怎样摆放它们才能重合呢?由三角形重合你能发现什么结论?同学们小组讨论、交流,归纳得出结论。
几何语言:
对应边
对应角
A
B
C
D
E
F
A
B
C
D
E
F
?ABC≌
?DEF,看下列各组对应元素的等量关系,你发现了什么?
(1)∠B=∠E,A
C=D
F;(2)∠B=∠E,∠A=∠D,AB=DE;
(3)BC=
E
F,∠A=∠D;(4)AB=AC,DE=DF,∠A=∠D;
1.全等三角形中对应角的对边是对应边,两个对应角所夹的边是对应边;
2.全等三角形中对应边的对角是对应角,两条对应边所夹的角是对应角。
活动3
观察2
下面各图中的三角形全等吗?
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
(图1)
(图2)
(图3)
(1)图1中,
△ABC沿直线BC,得到
△DEF
。
(2)图2中,
△ABC沿直线BC翻折180度,得到△DBC。
(3)图3中,
△ABC旋转180度,得到△AED。
1.若△AOC≌△BOD,AC=
,∠A=
.
A
B
O
C
D
2.若△ABD≌△ACE,BD=
,∠BDA=
.
3.若△ABC≌△CDA,AB=
,∠BAC=
.
A
B
C
D
请填空:
A
B
C
D
E
对顶角
公共角
公共边
练一练
∠B
BD
CE
∠CEA
CD
∠DCA
试一试
讨论总结:根据以上图形,归纳找全等三角形对应元素的方法。
试一试
a.全等三角形中对应角的对边是对应边,两个对应角所夹的边是对应边;
b.全等三角形中对应边的对角是对应角,两条对应边所夹的角是对应角;
c.有公共边的,公共边一定是对应边;
d.有公共角的,公共角一定是对应角;
e.有对顶角的,对顶角一定是对应角;
f.一对最长的边是对应边,一对最短的边是对应边;一对最大的角是对应角,一对最小的角是对应角。
讨论总结:根据以上图形,归纳找全等三角形对应元素的方法。
1.全等形中可以不同的是(
)
A.图形的位置 B.图形的形状
C.图形的周长
D.图形的面积
A
[归纳]
(1)全等形:能够____________的两个图形,叫做全等形.
(2)判定两个图形全等的方法:两个图形只要满足_________相同,并且_________相等,它们就是全等形;平移、旋转、翻折前后的图形全等.
完全重合
形状
大小
小试牛刀
2.如右图,已知△ABC≌△DEC,B和E,A和D是对应顶点,说出这两个三角形中对应的边和角。
3.如右图,已知△ABD≌△ACE,
且∠C=45°,AC
=
5,AE
=
3,则
∠B
=
,
DC
=
.
A
E
B
C
D
2
45°
D
B
E
A
C
如图,△ABC≌△DEC,CA和CD,CB和CE是对应边,
∠
ACD和∠BCE相等吗?为什么?
D
B
E
A
C
解:∠
ACD=∠BCE
理由:
∵
△ABC≌△DEC,
∴
∠
DCE
=∠ACB,
又∵
∠
ACD
=
∠
DCE
-
∠
1,
∠BCE
=
∠ACB
-
∠
1,
∴
∠
ACD
=
∠BCE.
1
思考提升
课堂小结
1.全等形、全等三角形的概念;
2.全等三角形的性质;
3.全等三角形的表示方法;
4.全等三角形中的对应关系。
这节课你学会了什么?有哪些收获?有什么感受?请把你的想法告诉你的同桌,然后告诉老师。
试一试
归纳:找全等三角形中对应元素的方法。
A
B
C
D
E
F
?ABC≌
?DEF,看下列各组对应元素的等量关系,你发现了什么?
(1)∠B=∠E,A
C=D
F;(2)∠B=∠E,∠A=∠D,AB=DE;
(3)BC=
E
F,∠A=∠D;(4)AB=AC,DE=DF,∠A=∠D;
1.全等三角形中对应角的对边是对应边,两个对应角所夹的边是对应边;
2.全等三角形中对应边的对角是对应角,两条对应边所夹的角是对应角;
活动3
观察下面的图形变换,找出全等三角形,并指出对应边和对应角。
A
B
C
D
A
B
C
D
O
A
B
C
D
E
3.有公共边的,公共边一定是对应边;
4.有公共角的,公共角一定是对应角;
5.有对顶角的,对顶角一定是对应角;
观察
C
A
B
F
E
D
对应边是:
对应角是:
AC与DF,AB与DE,BC与EF
∠A与∠D,∠B与∠E,∠C与∠F
6.一对最长的边是对应边,一对最短的边是对应边;
一对最大的角是对应角,一对最小的角是对应角;
1.全等三角形中对应角的对边是对应边,两个对应角所夹的边是对应边;
2.全等三角形中对应边的对角是对应角,两条对应边所夹的角是对应角;
3.有公共边的,公共边一定是对应边;
4.有公共角的,公共角一定是对应角;
5.有对顶角的,对顶角一定是对应角;
6.一对最长的边是对应边,一对最短的边是对应边;一对最大的角是对应角,一对最小的角是对应角。
