6.3.4 等可能事件的概率(4)课件(共19张PPT)
文档属性
| 名称 | 6.3.4 等可能事件的概率(4)课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 760.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-06 09:26:26 | ||
图片预览






文档简介
6.3.4等可能事件的概率(4)
第六章 概率初步
2020-2021北师大版七年级数学下册
学习目标
1.理解等可能事件的意义;
2.理解等可能事件概率的意义;(重点)
3.学会利用等可能事件的概率解决实际概率问题。(难点)
概率的计算方法
事件A发生的概率表示为
P(A)=
事件A发生的结果数
所有可能的结果总数
该事件所占区域的面积
所求事件的概率= —————————
总面积
导入新课
如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在蓝色区域和红色区域的概率分别是多少?
1200
红
蓝
与面积相关的等可能事件概率
探究新知
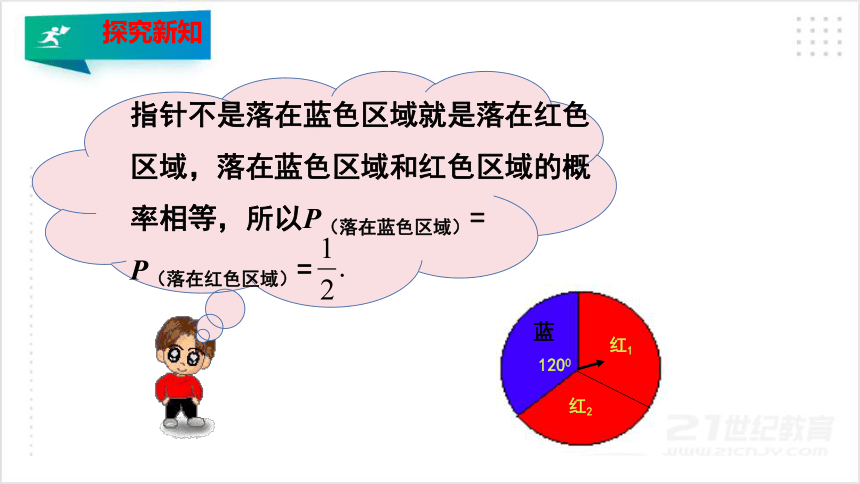
指针不是落在蓝色区域就是落在红色区域,落在蓝色区域和红色区域的概率相等,所以P(落在蓝色区域)=
P(落在红色区域)=
1200
红1
蓝
红2
探究新知
先把红色区域等分成2份,这样转盘被分成3个扇形区域,其中1个是蓝色,2个是红色,所以P(落在蓝色区域)=
P(落在红色区域) =
1200
红1
蓝
红2
探究新知
各种结果出现的可能性务必相同。
转盘应被等分成若干份。
注意:
探究新知
转动如图所示的转盘,当转盘停止时,指针落在红色区域和蓝色区域的概率分别是多少?
想一想
1100
红
蓝
探究新知
例1 某路口南北方向红绿灯的设置时间为:红灯20秒、绿灯60秒、黄灯3秒.小明的爸爸随机地由南往北开车经过该路口,问:
(1)他遇到红灯的概率大还是遇到绿灯的概率大?
(2)他遇到红灯的概率是多少?
例题讲解
解:(1)小明的爸爸随机地经过该路口,他每一时刻经过的可能性都相同.因为该路口南北方向红绿灯的设置时间为:红灯40s,绿灯60s,黄灯3s.绿灯时间比红灯时间长,所以他遇到绿灯的概率大.
(2)他遇到红灯的概率为:
例题讲解
例2 如图所示是一个转盘,转盘分成7个相同的扇形,颜色分为红黄绿三种,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时当作指向右边的扇形)求下列事件的概率.
(1)指向红色;
(2)指向红色或黄色;
(3)不指向红色.
例题讲解
解:一共有7种等可能的结果.
(1)指向红色有3种结果,
P(指向红色)=_____;
(2)指向红色或黄色一共有5种
等可能的结果,P( 指向红或黄)=_____;
(3)不指向红色有4种等可能的结果
P( 不指向红色)= ______.
例题讲解
1.如图,把一个圆形转盘按1∶2∶3∶4的比例分成A、B、C、D四个扇形区域,自由转动转盘,停止后指针落在B区域的概率为________.
解析:∵一个圆形转盘按1∶2∶3∶4
的比例分成A、B、C、D四个扇形区域,
∴圆形转盘被等分成10份,其中B区域
占2份,∴P(落在B区域)=
课堂练习
2.如图,能自由转动的转盘中, A、B、C、D四个扇形的圆心角的度数分别为180°、 30 °、 60 °、 90 °,转动转盘,当转盘停止时, 指针指向B的概率是_____,指向C或D的概率是_____.
A
B
C
D
课堂练习
3.某电视频道播放正片与广告的时间之比为7:1,广告随机穿插在正片之间,小明随机地打开电视机,收看该频道,他开机就能看到正片的概率是多少?
课堂练习
4.如图是一个转盘,扇形1,2,3,4,5所对的圆心角分别是180°,90°,45°,30°,15°,任意转动转盘,求出指针分别指向1,2,3,4,5的概率(指针恰好指向两扇形交线的概率视为零).
课堂练习
课堂小结
C、在生活中要善于应用数学知识。
A、公式总结:
该事件所占区域的面积
所求事件的概率 = ————————————
总面积
B、各种结果出现的可能性务必相同。
https://www.21cnjy.com/help/help_extract.php
第六章 概率初步
2020-2021北师大版七年级数学下册
学习目标
1.理解等可能事件的意义;
2.理解等可能事件概率的意义;(重点)
3.学会利用等可能事件的概率解决实际概率问题。(难点)
概率的计算方法
事件A发生的概率表示为
P(A)=
事件A发生的结果数
所有可能的结果总数
该事件所占区域的面积
所求事件的概率= —————————
总面积
导入新课
如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在蓝色区域和红色区域的概率分别是多少?
1200
红
蓝
与面积相关的等可能事件概率
探究新知
指针不是落在蓝色区域就是落在红色区域,落在蓝色区域和红色区域的概率相等,所以P(落在蓝色区域)=
P(落在红色区域)=
1200
红1
蓝
红2
探究新知
先把红色区域等分成2份,这样转盘被分成3个扇形区域,其中1个是蓝色,2个是红色,所以P(落在蓝色区域)=
P(落在红色区域) =
1200
红1
蓝
红2
探究新知
各种结果出现的可能性务必相同。
转盘应被等分成若干份。
注意:
探究新知
转动如图所示的转盘,当转盘停止时,指针落在红色区域和蓝色区域的概率分别是多少?
想一想
1100
红
蓝
探究新知
例1 某路口南北方向红绿灯的设置时间为:红灯20秒、绿灯60秒、黄灯3秒.小明的爸爸随机地由南往北开车经过该路口,问:
(1)他遇到红灯的概率大还是遇到绿灯的概率大?
(2)他遇到红灯的概率是多少?
例题讲解
解:(1)小明的爸爸随机地经过该路口,他每一时刻经过的可能性都相同.因为该路口南北方向红绿灯的设置时间为:红灯40s,绿灯60s,黄灯3s.绿灯时间比红灯时间长,所以他遇到绿灯的概率大.
(2)他遇到红灯的概率为:
例题讲解
例2 如图所示是一个转盘,转盘分成7个相同的扇形,颜色分为红黄绿三种,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时当作指向右边的扇形)求下列事件的概率.
(1)指向红色;
(2)指向红色或黄色;
(3)不指向红色.
例题讲解
解:一共有7种等可能的结果.
(1)指向红色有3种结果,
P(指向红色)=_____;
(2)指向红色或黄色一共有5种
等可能的结果,P( 指向红或黄)=_____;
(3)不指向红色有4种等可能的结果
P( 不指向红色)= ______.
例题讲解
1.如图,把一个圆形转盘按1∶2∶3∶4的比例分成A、B、C、D四个扇形区域,自由转动转盘,停止后指针落在B区域的概率为________.
解析:∵一个圆形转盘按1∶2∶3∶4
的比例分成A、B、C、D四个扇形区域,
∴圆形转盘被等分成10份,其中B区域
占2份,∴P(落在B区域)=
课堂练习
2.如图,能自由转动的转盘中, A、B、C、D四个扇形的圆心角的度数分别为180°、 30 °、 60 °、 90 °,转动转盘,当转盘停止时, 指针指向B的概率是_____,指向C或D的概率是_____.
A
B
C
D
课堂练习
3.某电视频道播放正片与广告的时间之比为7:1,广告随机穿插在正片之间,小明随机地打开电视机,收看该频道,他开机就能看到正片的概率是多少?
课堂练习
4.如图是一个转盘,扇形1,2,3,4,5所对的圆心角分别是180°,90°,45°,30°,15°,任意转动转盘,求出指针分别指向1,2,3,4,5的概率(指针恰好指向两扇形交线的概率视为零).
课堂练习
课堂小结
C、在生活中要善于应用数学知识。
A、公式总结:
该事件所占区域的面积
所求事件的概率 = ————————————
总面积
B、各种结果出现的可能性务必相同。
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
