5.3.3 简单的轴对称图形 同步练习(含答案)
文档属性
| 名称 | 5.3.3 简单的轴对称图形 同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-06 09:35:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
5.3.3 简单的轴对称图形同步练习
一、选择题。
1.到三角形的三边距离相等的点是( )
A.三角形三条高的交点
B.三角形三条内角平分线的交点
C.三角形三条中线的交点
D.三角形三条边的垂直平分线的交点
2.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF⊥AB,交AB于点F,交BE于点D,若BC=8cm,DF=3cm,则△CDB的面积为( )
A.12cm2 B.8cm2 C.6cm2 D.4cm2
3.如图,点P在∠ABC的平分线上,PD⊥BC于点D,若PD=4,则P到BA的距离为( )
A.3 B.4 C.5 D.6
4.如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
A.80° B.60° C.40° D.30°
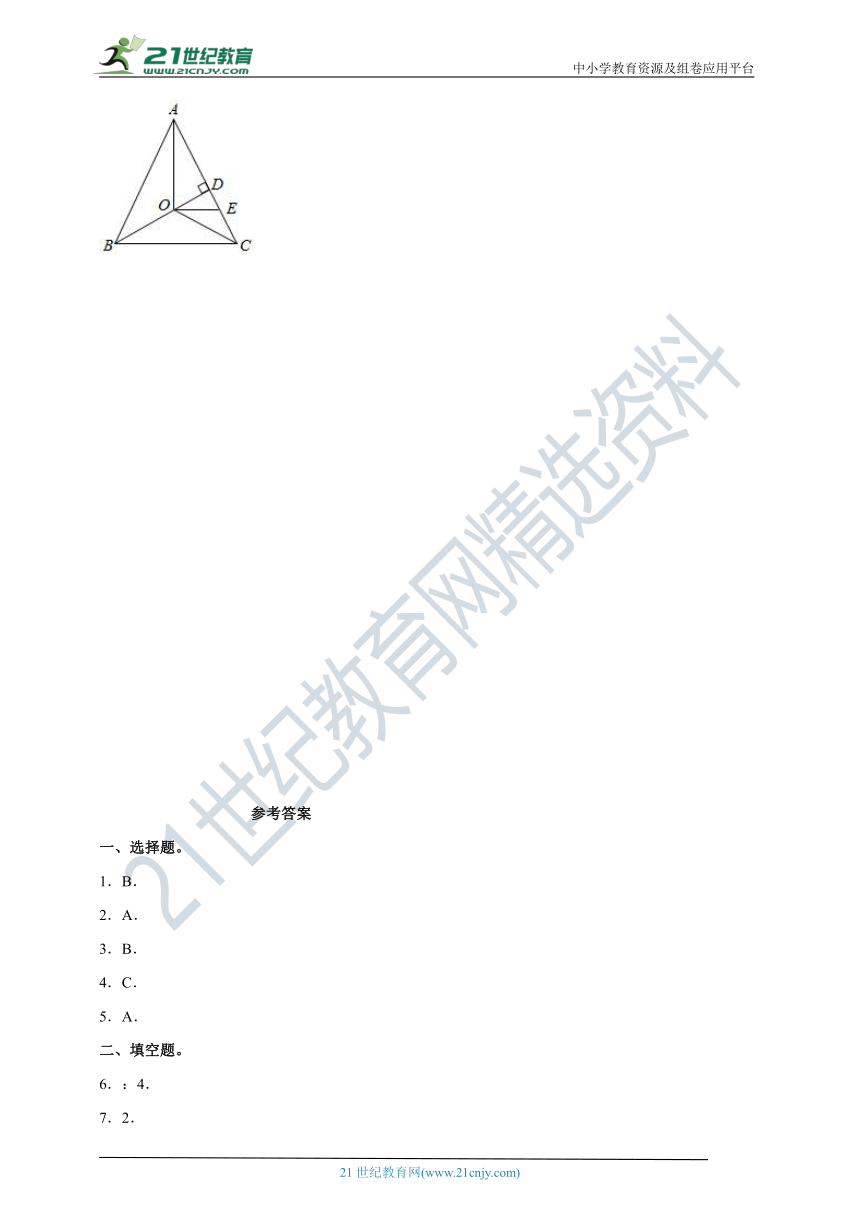
5.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠CDE;③DE=BE; ④AD=AB+CD,四个结论中成立的是( )
A.①②④ B.①②③ C.②③④ D.①③
二、填空题。
6.如图,△ABC中,∠C=90°,AD平分∠CAB,且BC=12,BD=8,则点D到AB的距离为 .
7.如图,已知△ABC的周长是20,面积是30,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,则
OD长 .
8.如图,直线a、b、c分别表示相互交叉的马路,要建一个停车场要求到三条马路的距离相等,那么符合条件的修建点有 处.
9.如图,BH是钝角三角形ABC的高,AD是角平分线,且2∠C=90°﹣∠ABH,若CD=4,△ABC的面积为12,则AD= .
10.如图点D是△ABC的两外角平分线的交点,下列说法:
①AD=CD;
②AB=AC;
③D到AB、BC所在直线的距离相等;
@点D在∠B的平分线上;
其中正确的说法的序号是 .
解答题。
11.如图,在△ABC中,∠A=∠ACB,CD为△ABC的角平分线,CE是△ABC的高.
(1)若∠DCB=15°,求∠CBD的度数;
(2)若∠DCE=36°,求∠ACB的度数.
12.如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
13.已知:在△ABC中,AB=AC,BD⊥AC交AC于D,AO平分∠BAC交BD于O,过O点作OE∥BC交AC于E.
(1)求证:BO=OC;
(2)若∠BAC=56°,求∠DOE的度数.
参考答案
一、选择题。
1.B.
2.A.
3.B.
4.C.
5.A.
二、填空题。
6.:4.
7.2.
8.:四.
9.3.
10.③④.
三、解答题。
11.【解答】解:(1)∵CD为△ABC的角平分线,
∴∠ACB=2∠DCB=2×15°=30°,
∵∠A=∠ACB,
∴∠CBD=180°﹣∠A﹣∠ACB=180°﹣30°﹣30°=120°;
(2)设∠A=∠ACB=x,
∵CE是△ABC的高,∠DCE=36°,
∴∠CDE=90°﹣36°=54°,
∵CD为△ABC的角平分线,
∴∠ACD=∠ACB=x,
由三角形的外角性质得,∠CDE=∠A+∠ACD,
∴x+x=54°,
解得x=36°,
即∠ACB=36°.
12.【解答】解:如图,点P为所作.
13.【解答】解:(1)∵AO平分∠BAC,
∴∠BAO=∠OAC,
在△ABO和△ACO中,
,
∴△ABO≌△ACO(SAS),
∴BO=OC.
(2)∵BD⊥AC,
∴∠BDC=90°,
∴∠ABD=∠BDC﹣∠BAD=90°﹣56°=34°,
∵AB=AC,
∴∠ABC=∠ACB=(180°﹣∠BAC)=62°,
∴∠DBC=∠ABC﹣∠ABD=62°﹣34°=28°,
∵OE∥BC,
∴∠DOE=∠DBC=28°.
_21?????????è?????(www.21cnjy.com)_
5.3.3 简单的轴对称图形同步练习
一、选择题。
1.到三角形的三边距离相等的点是( )
A.三角形三条高的交点
B.三角形三条内角平分线的交点
C.三角形三条中线的交点
D.三角形三条边的垂直平分线的交点
2.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF⊥AB,交AB于点F,交BE于点D,若BC=8cm,DF=3cm,则△CDB的面积为( )
A.12cm2 B.8cm2 C.6cm2 D.4cm2
3.如图,点P在∠ABC的平分线上,PD⊥BC于点D,若PD=4,则P到BA的距离为( )
A.3 B.4 C.5 D.6
4.如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
A.80° B.60° C.40° D.30°
5.如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠CDE;③DE=BE; ④AD=AB+CD,四个结论中成立的是( )
A.①②④ B.①②③ C.②③④ D.①③
二、填空题。
6.如图,△ABC中,∠C=90°,AD平分∠CAB,且BC=12,BD=8,则点D到AB的距离为 .
7.如图,已知△ABC的周长是20,面积是30,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,则
OD长 .
8.如图,直线a、b、c分别表示相互交叉的马路,要建一个停车场要求到三条马路的距离相等,那么符合条件的修建点有 处.
9.如图,BH是钝角三角形ABC的高,AD是角平分线,且2∠C=90°﹣∠ABH,若CD=4,△ABC的面积为12,则AD= .
10.如图点D是△ABC的两外角平分线的交点,下列说法:
①AD=CD;
②AB=AC;
③D到AB、BC所在直线的距离相等;
@点D在∠B的平分线上;
其中正确的说法的序号是 .
解答题。
11.如图,在△ABC中,∠A=∠ACB,CD为△ABC的角平分线,CE是△ABC的高.
(1)若∠DCB=15°,求∠CBD的度数;
(2)若∠DCE=36°,求∠ACB的度数.
12.如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
13.已知:在△ABC中,AB=AC,BD⊥AC交AC于D,AO平分∠BAC交BD于O,过O点作OE∥BC交AC于E.
(1)求证:BO=OC;
(2)若∠BAC=56°,求∠DOE的度数.
参考答案
一、选择题。
1.B.
2.A.
3.B.
4.C.
5.A.
二、填空题。
6.:4.
7.2.
8.:四.
9.3.
10.③④.
三、解答题。
11.【解答】解:(1)∵CD为△ABC的角平分线,
∴∠ACB=2∠DCB=2×15°=30°,
∵∠A=∠ACB,
∴∠CBD=180°﹣∠A﹣∠ACB=180°﹣30°﹣30°=120°;
(2)设∠A=∠ACB=x,
∵CE是△ABC的高,∠DCE=36°,
∴∠CDE=90°﹣36°=54°,
∵CD为△ABC的角平分线,
∴∠ACD=∠ACB=x,
由三角形的外角性质得,∠CDE=∠A+∠ACD,
∴x+x=54°,
解得x=36°,
即∠ACB=36°.
12.【解答】解:如图,点P为所作.
13.【解答】解:(1)∵AO平分∠BAC,
∴∠BAO=∠OAC,
在△ABO和△ACO中,
,
∴△ABO≌△ACO(SAS),
∴BO=OC.
(2)∵BD⊥AC,
∴∠BDC=90°,
∴∠ABD=∠BDC﹣∠BAD=90°﹣56°=34°,
∵AB=AC,
∴∠ABC=∠ACB=(180°﹣∠BAC)=62°,
∴∠DBC=∠ABC﹣∠ABD=62°﹣34°=28°,
∵OE∥BC,
∴∠DOE=∠DBC=28°.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
