22.2 二次函数与一元二次方程 同步练习试卷 2020——2021学年人教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 22.2 二次函数与一元二次方程 同步练习试卷 2020——2021学年人教版九年级数学上册(Word版含答案) | 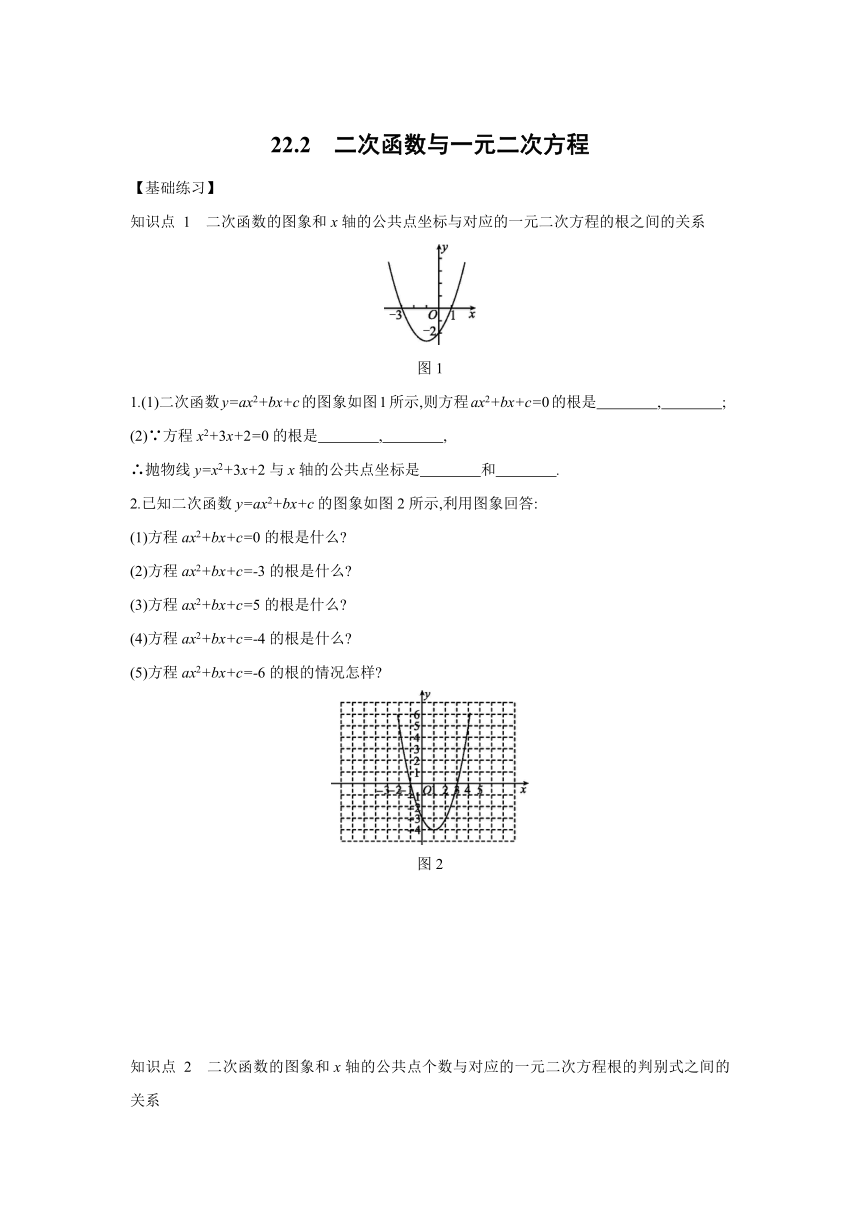 | |
| 格式 | doc | ||
| 文件大小 | 294.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 07:42:23 | ||
图片预览




文档简介
22.2 二次函数与一元二次方程
【基础练习】
知识点 1 二次函数的图象和x轴的公共点坐标与对应的一元二次方程的根之间的关系
图1
1.(1)二次函数y=ax2+bx+c的图象如图1所示,则方程ax2+bx+c=0的根是 , ;?
(2)∵方程x2+3x+2=0的根是 , ,?
∴抛物线y=x2+3x+2与x轴的公共点坐标是 和 .?
2.已知二次函数y=ax2+bx+c的图象如图2所示,利用图象回答:
(1)方程ax2+bx+c=0的根是什么?
(2)方程ax2+bx+c=-3的根是什么?
(3)方程ax2+bx+c=5的根是什么?
(4)方程ax2+bx+c=-4的根是什么?
(5)方程ax2+bx+c=-6的根的情况怎样?
图2
知识点 2 二次函数的图象和x轴的公共点个数与对应的一元二次方程根的判别式之间的关系
3.已知抛物线y=x2-6x+m-1,当m 时,抛物线与x轴有两个公共点;当m 时,抛物线与x轴有一个公共点;当m 时,抛物线与x轴没有公共点.?
4.若二次函数y=x2-4x+n的图象与x轴只有一个公共点,则实数n= .?
5.[2020·宁夏] 若二次函数y=-x2+2x+k的图象与x轴有两个公共点,则k的取值范围是 .?
6.已知二次函数y=x2-x+m-1的图象与x轴有公共点,则m的取值范围是 .?
知识点 3 利用二次函数的图象求一元二次方程的根的近似值
7.如图3是二次函数y=ax2+bx+c的图象,图象上有两点分别为A(2.18,-0.51),B(2.68,0.54),则方程ax2+bx+c=0的一个根可能是 ( )
图3
A.2.18 B.2.68 C.-0.51 D.2.45
8.[教材习题22.2第2题变式] 利用二次函数的图象求一元二次方程x2-2x-1=0的实数根.(精确到0.1)
知识点 4 利用二次函数的图象解一元二次不等式
9.如图4是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
图4
A.-15
C.x<-1 D.x<-1或x>5
10.画出二次函数y=x2-2x的图象.利用图象回答:
(1)当x取什么值时,函数值大于0?
(2)当x取什么值时,函数值小于0?
(3)当x取什么值时,函数值小于3?
(4)当x取什么值时,函数值大于3?
【能力提升】
11.[2019·荆门] 抛物线y=-x2+4x-4与坐标轴的公共点个数为 ( )
A.0 B.1 C.2 D.3
12.在平面直角坐标系xOy中,二次函数y=ax2+bx+c的大致图象如图5所示,则下列结论正确的是 ( )
图5
A.a<0,b<0,c>0
B.-=1
C.a+b+c<0
D.关于x的方程ax2+bx+c=-1有两个不相等的实数根
13.函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y<0成立的x的取值范围是 ( )
A.x<-4或x>2 B.-42 D.014.若函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个公共点,则a的值为 .?
15.若关于x的一元二次方程a(x+m)2-3=0的两个实数根分别为x1=-1,x2=3,则抛物线y=a(x+m-2)2-3与x轴的公共点坐标为 .?
16.已知函数y=-x2+(m-1)x+m(m为常数).
(1)该函数的图象与x轴的公共点个数是 ( )
A.0 B.1 C.2 D.1或2
(2)求证:不论m为何值,该函数图象的顶点都在函数y=(x+1)2的图象上;
(3)当-2≤m≤3时,求该函数图象的顶点纵坐标的取值范围.
答案
1.(1)x1=-3 x2=1
(2)x1=-2 x2=-1 (-2,0) (-1,0)
2.解:(1)方程ax2+bx+c=0的根是x1=-1,x2=3.
(2)方程ax2+bx+c=-3的根是x1=0,x2=2.
(3)方程ax2+bx+c=5的根是x1=-2,x2=4.
(4)方程ax2+bx+c=-4的根是x1=x2=1.
(5)方程ax2+bx+c=-6无实数根.
3.<10 =10 >10
[解析] Δ=b2-4ac=(-6)2-4(m-1)=-4m+40.
当Δ>0,即-4m+40>0,m<10时,
抛物线与x轴有两个公共点;
当Δ=0,即-4m+40=0,m=10时,
抛物线与x轴有一个公共点;
当Δ<0,即-4m+40<0,m>10时,
抛物线与x轴没有公共点.
4.4 [解析] 二次函数y=x2-4x+n的图象与x轴只有一个公共点,说明“Δ=b2-4ac=0”,即(-4)2-4×1×n=0,所以n=4.
5.k>-1 [解析] ∵二次函数y=-x2+2x+k的图象与x轴有两个公共点,
∴Δ=b2-4ac=4-4×(-1)·k>0,解得k>-1.
6.m≤5 [解析] 因为抛物线y=x2-x+m-1与x轴有公共点,所以(-1)2-4×1×(m-1)≥0,解得m≤5.
7.D [解析] 因为图象上有两点分别为A(2.18,-0.51),B(2.68,0.54),
所以当x=2.18时,y=-0.51;当x=2.68时,y=0.54,
所以当y=0时,2.18<一个根<2.68,只有选项D符合.故选D.
8.解:方程x2-2x-1=0的根是函数y=x2-2x-1的图象与x轴的公共点的横坐标.作出二次函数y=x2-2x-1的图象(如图).
由图象可知方程有两个根,一个根在-1和0之间,另一个根在2和3之间.
先求-1和0之间的根.
当x=-0.4时,y=-0.04;
当x=-0.5时,y=0.25.
因此,-0.4是方程的一个近似根.
同理,2.4是方程的另一个近似根.
综上,方程x2-2x-1=0的实数根为x1≈-0.4,x2≈2.4.
9.D [解析] 观察图象可知抛物线的对称轴为直线x=2,且抛物线与x轴的一个交点坐标是(5,0).依据抛物线的对称性可求出抛物线与x轴的另一个交点坐标为(-1,0).由二次函数y=ax2+bx+c的图象可知不等式ax2+bx+c<0的解集是x<-1或x>5.故选D.
10.解:列表:
x … -2 -1 0 1 2 3 4 …
y … 8 3 0 -1 0 3 8 …
描点并连线,如图所示:
(1)当x<0或x>2时,函数值大于0.
(2)当0(3)当-1(4)当x<-1或x>3时,函数值大于3.
11.C [解析] 当x=0时,y=-x2+4x-4=-4,则抛物线与y轴的公共点坐标为(0,-4);当y=0时,-x2+4x-4=0,解得x1=x2=2,则抛物线与x轴的公共点坐标为(2,0),所以抛物线与坐标轴有2个公共点.故选C.
12.D [解析] (1)因为抛物线的开口向下,所以a<0.因为抛物线的对称轴在y轴的右侧,所以->0,所以b>0.因为抛物线与y轴的负半轴相交,所以c<0.可见选项A错误.
(2)因为对称轴在直线x=1的右侧,所以->1.可见选项B错误.
(3)因为抛物线经过点(1,0),所以当x=1时,y=0,即a+b+c=0.可见选项C错误.
(4)由图象可知,y的最大值是1,所以直线y=-1与抛物线有两个公共点,即关于x的方程ax2+bx+c=-1有两个不相等的实数根.可见选项D正确.
综上所述,只有选项D中的结论是正确的,故选D.
13.A [解析] 因为a<0,所以抛物线开口向下.因为抛物线的对称轴为直线x=-=-1,抛物线过点(2,0),所以抛物线与x轴的另一个公共点坐标为(-4,0).故使y<0成立的x的取值范围是x<-4或x>2.
14.-1或2或1 [解析] 因为函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个公共点.
当函数为二次函数时,
a-1≠0,Δ=16-4(a-1)×2a=0,
解得a1=-1,a2=2;
当函数为一次函数时,
a-1=0,解得a=1.
综上,a的值为-1或2或1.
15.(1,0),(5,0) [解析] 因为关于x的一元二次方程a(x+m)2-3=0的两个实数根分别为x1=-1,x2=3,
即抛物线y=a(x+m)2-3与x轴的两个公共点坐标是(-1,0),(3,0).
抛物线y=a(x+m-2)2-3是将抛物线y=a(x+m)2-3向右平移2个单位长度得到的,
所以抛物线y=a(x+m-2)2-3与x轴的公共点坐标是(1,0),(5,0).
16.解:(1)二次函数对应的一元二次方程为-x2+(m-1)x+m=0,
则b2-4ac=(m-1)2+4m=(m+1)2≥0,
所以一元二次方程有两个相等或两个不相等的实数根,
即对应的二次函数图象与x轴有1个或2个公共点.故选D.
(2)证明:y=-x2+(m-1)x+m=-(x-)2+,
所以该函数图象的顶点坐标为(,).
把x=代入y=(x+1)2,得y=(+1)2=.
因此,不论m为何值,该函数图象的顶点都在函数y=(x+1)2的图象上.
(3)设z=.
当m=-1时,z有最小值0;
当m<-1时,z随m的增大而减小;
当m>-1时,z随m的增大而增大.
又当m=-2时,z==;
当m=3时,z==4.
所以当-2≤m≤3时,该函数图象的顶点纵坐标z的取值范围是0≤z≤4.
【基础练习】
知识点 1 二次函数的图象和x轴的公共点坐标与对应的一元二次方程的根之间的关系
图1
1.(1)二次函数y=ax2+bx+c的图象如图1所示,则方程ax2+bx+c=0的根是 , ;?
(2)∵方程x2+3x+2=0的根是 , ,?
∴抛物线y=x2+3x+2与x轴的公共点坐标是 和 .?
2.已知二次函数y=ax2+bx+c的图象如图2所示,利用图象回答:
(1)方程ax2+bx+c=0的根是什么?
(2)方程ax2+bx+c=-3的根是什么?
(3)方程ax2+bx+c=5的根是什么?
(4)方程ax2+bx+c=-4的根是什么?
(5)方程ax2+bx+c=-6的根的情况怎样?
图2
知识点 2 二次函数的图象和x轴的公共点个数与对应的一元二次方程根的判别式之间的关系
3.已知抛物线y=x2-6x+m-1,当m 时,抛物线与x轴有两个公共点;当m 时,抛物线与x轴有一个公共点;当m 时,抛物线与x轴没有公共点.?
4.若二次函数y=x2-4x+n的图象与x轴只有一个公共点,则实数n= .?
5.[2020·宁夏] 若二次函数y=-x2+2x+k的图象与x轴有两个公共点,则k的取值范围是 .?
6.已知二次函数y=x2-x+m-1的图象与x轴有公共点,则m的取值范围是 .?
知识点 3 利用二次函数的图象求一元二次方程的根的近似值
7.如图3是二次函数y=ax2+bx+c的图象,图象上有两点分别为A(2.18,-0.51),B(2.68,0.54),则方程ax2+bx+c=0的一个根可能是 ( )
图3
A.2.18 B.2.68 C.-0.51 D.2.45
8.[教材习题22.2第2题变式] 利用二次函数的图象求一元二次方程x2-2x-1=0的实数根.(精确到0.1)
知识点 4 利用二次函数的图象解一元二次不等式
9.如图4是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
图4
A.-1
C.x<-1 D.x<-1或x>5
10.画出二次函数y=x2-2x的图象.利用图象回答:
(1)当x取什么值时,函数值大于0?
(2)当x取什么值时,函数值小于0?
(3)当x取什么值时,函数值小于3?
(4)当x取什么值时,函数值大于3?
【能力提升】
11.[2019·荆门] 抛物线y=-x2+4x-4与坐标轴的公共点个数为 ( )
A.0 B.1 C.2 D.3
12.在平面直角坐标系xOy中,二次函数y=ax2+bx+c的大致图象如图5所示,则下列结论正确的是 ( )
图5
A.a<0,b<0,c>0
B.-=1
C.a+b+c<0
D.关于x的方程ax2+bx+c=-1有两个不相等的实数根
13.函数y=ax2+2ax+m(a<0)的图象过点(2,0),则使函数值y<0成立的x的取值范围是 ( )
A.x<-4或x>2 B.-4
15.若关于x的一元二次方程a(x+m)2-3=0的两个实数根分别为x1=-1,x2=3,则抛物线y=a(x+m-2)2-3与x轴的公共点坐标为 .?
16.已知函数y=-x2+(m-1)x+m(m为常数).
(1)该函数的图象与x轴的公共点个数是 ( )
A.0 B.1 C.2 D.1或2
(2)求证:不论m为何值,该函数图象的顶点都在函数y=(x+1)2的图象上;
(3)当-2≤m≤3时,求该函数图象的顶点纵坐标的取值范围.
答案
1.(1)x1=-3 x2=1
(2)x1=-2 x2=-1 (-2,0) (-1,0)
2.解:(1)方程ax2+bx+c=0的根是x1=-1,x2=3.
(2)方程ax2+bx+c=-3的根是x1=0,x2=2.
(3)方程ax2+bx+c=5的根是x1=-2,x2=4.
(4)方程ax2+bx+c=-4的根是x1=x2=1.
(5)方程ax2+bx+c=-6无实数根.
3.<10 =10 >10
[解析] Δ=b2-4ac=(-6)2-4(m-1)=-4m+40.
当Δ>0,即-4m+40>0,m<10时,
抛物线与x轴有两个公共点;
当Δ=0,即-4m+40=0,m=10时,
抛物线与x轴有一个公共点;
当Δ<0,即-4m+40<0,m>10时,
抛物线与x轴没有公共点.
4.4 [解析] 二次函数y=x2-4x+n的图象与x轴只有一个公共点,说明“Δ=b2-4ac=0”,即(-4)2-4×1×n=0,所以n=4.
5.k>-1 [解析] ∵二次函数y=-x2+2x+k的图象与x轴有两个公共点,
∴Δ=b2-4ac=4-4×(-1)·k>0,解得k>-1.
6.m≤5 [解析] 因为抛物线y=x2-x+m-1与x轴有公共点,所以(-1)2-4×1×(m-1)≥0,解得m≤5.
7.D [解析] 因为图象上有两点分别为A(2.18,-0.51),B(2.68,0.54),
所以当x=2.18时,y=-0.51;当x=2.68时,y=0.54,
所以当y=0时,2.18<一个根<2.68,只有选项D符合.故选D.
8.解:方程x2-2x-1=0的根是函数y=x2-2x-1的图象与x轴的公共点的横坐标.作出二次函数y=x2-2x-1的图象(如图).
由图象可知方程有两个根,一个根在-1和0之间,另一个根在2和3之间.
先求-1和0之间的根.
当x=-0.4时,y=-0.04;
当x=-0.5时,y=0.25.
因此,-0.4是方程的一个近似根.
同理,2.4是方程的另一个近似根.
综上,方程x2-2x-1=0的实数根为x1≈-0.4,x2≈2.4.
9.D [解析] 观察图象可知抛物线的对称轴为直线x=2,且抛物线与x轴的一个交点坐标是(5,0).依据抛物线的对称性可求出抛物线与x轴的另一个交点坐标为(-1,0).由二次函数y=ax2+bx+c的图象可知不等式ax2+bx+c<0的解集是x<-1或x>5.故选D.
10.解:列表:
x … -2 -1 0 1 2 3 4 …
y … 8 3 0 -1 0 3 8 …
描点并连线,如图所示:
(1)当x<0或x>2时,函数值大于0.
(2)当0
11.C [解析] 当x=0时,y=-x2+4x-4=-4,则抛物线与y轴的公共点坐标为(0,-4);当y=0时,-x2+4x-4=0,解得x1=x2=2,则抛物线与x轴的公共点坐标为(2,0),所以抛物线与坐标轴有2个公共点.故选C.
12.D [解析] (1)因为抛物线的开口向下,所以a<0.因为抛物线的对称轴在y轴的右侧,所以->0,所以b>0.因为抛物线与y轴的负半轴相交,所以c<0.可见选项A错误.
(2)因为对称轴在直线x=1的右侧,所以->1.可见选项B错误.
(3)因为抛物线经过点(1,0),所以当x=1时,y=0,即a+b+c=0.可见选项C错误.
(4)由图象可知,y的最大值是1,所以直线y=-1与抛物线有两个公共点,即关于x的方程ax2+bx+c=-1有两个不相等的实数根.可见选项D正确.
综上所述,只有选项D中的结论是正确的,故选D.
13.A [解析] 因为a<0,所以抛物线开口向下.因为抛物线的对称轴为直线x=-=-1,抛物线过点(2,0),所以抛物线与x轴的另一个公共点坐标为(-4,0).故使y<0成立的x的取值范围是x<-4或x>2.
14.-1或2或1 [解析] 因为函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个公共点.
当函数为二次函数时,
a-1≠0,Δ=16-4(a-1)×2a=0,
解得a1=-1,a2=2;
当函数为一次函数时,
a-1=0,解得a=1.
综上,a的值为-1或2或1.
15.(1,0),(5,0) [解析] 因为关于x的一元二次方程a(x+m)2-3=0的两个实数根分别为x1=-1,x2=3,
即抛物线y=a(x+m)2-3与x轴的两个公共点坐标是(-1,0),(3,0).
抛物线y=a(x+m-2)2-3是将抛物线y=a(x+m)2-3向右平移2个单位长度得到的,
所以抛物线y=a(x+m-2)2-3与x轴的公共点坐标是(1,0),(5,0).
16.解:(1)二次函数对应的一元二次方程为-x2+(m-1)x+m=0,
则b2-4ac=(m-1)2+4m=(m+1)2≥0,
所以一元二次方程有两个相等或两个不相等的实数根,
即对应的二次函数图象与x轴有1个或2个公共点.故选D.
(2)证明:y=-x2+(m-1)x+m=-(x-)2+,
所以该函数图象的顶点坐标为(,).
把x=代入y=(x+1)2,得y=(+1)2=.
因此,不论m为何值,该函数图象的顶点都在函数y=(x+1)2的图象上.
(3)设z=.
当m=-1时,z有最小值0;
当m<-1时,z随m的增大而减小;
当m>-1时,z随m的增大而增大.
又当m=-2时,z==;
当m=3时,z==4.
所以当-2≤m≤3时,该函数图象的顶点纵坐标z的取值范围是0≤z≤4.
同课章节目录
