11.1.2三角形的高、中线、角平分线课件-人教版八年级数学上册(16张)
文档属性
| 名称 | 11.1.2三角形的高、中线、角平分线课件-人教版八年级数学上册(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
11.1.2
三角形的高、中线与角平分线
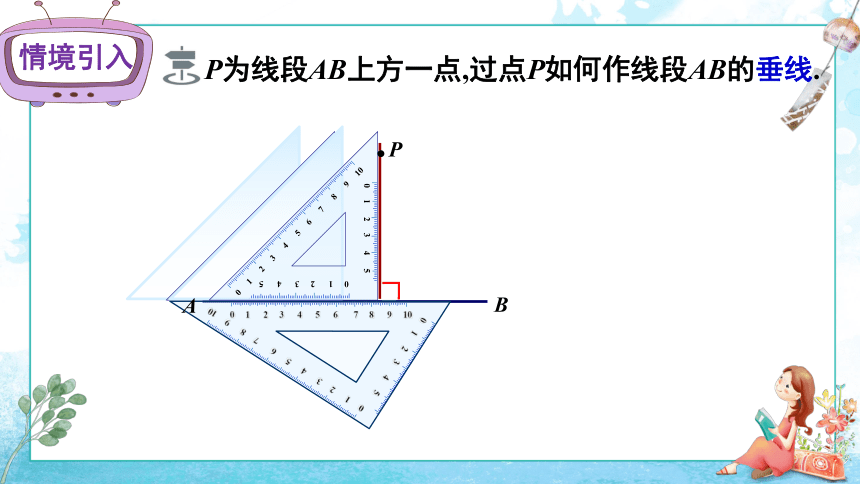
情境引入
P为线段AB上方一点,过点P如何作线段AB的垂线.
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
A
B
.P
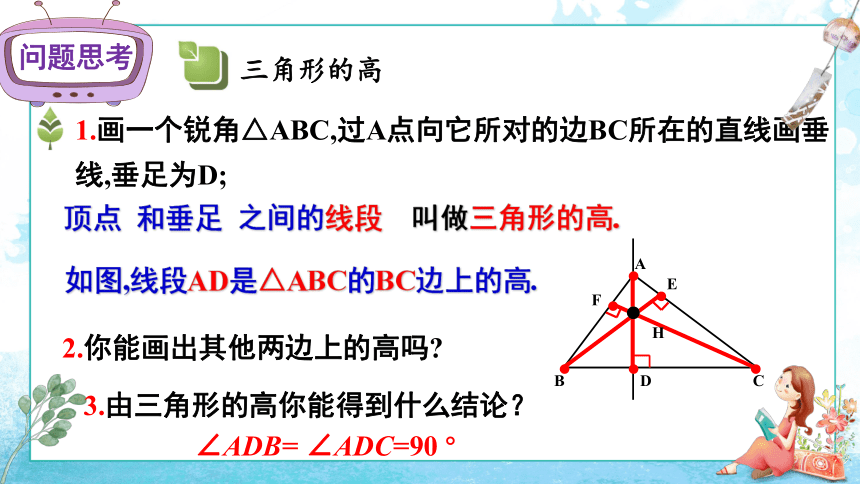
1.画一个锐角△ABC,过A点向它所对的边BC所在的直线画垂线,垂足为D;
问题思考
A
C
B
●
D
●
顶点
和垂足
之间的线段
叫做三角形的高.
如图,线段AD是△ABC的BC边上的高.
●
●
●
●
●
H
F
E
2.你能画出其他两边上的高吗?
3.由三角形的高你能得到什么结论?
∠ADB=
∠ADC=90
°
三角形的高
动手操作
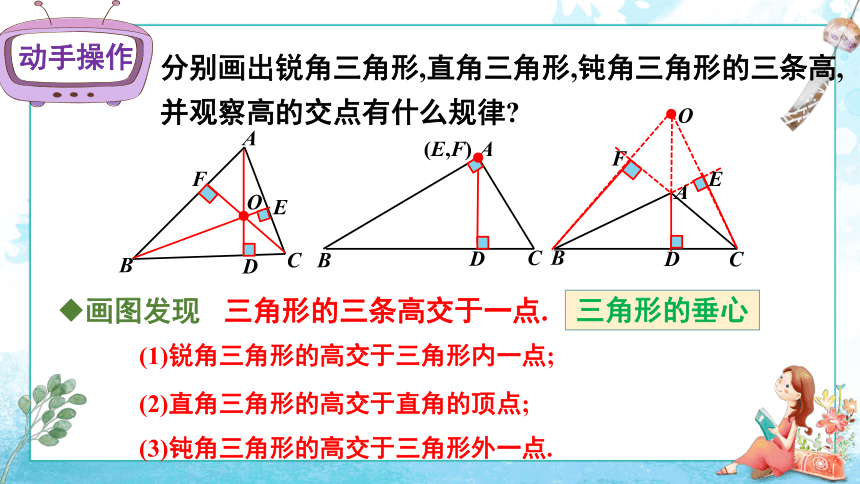
分别画出锐角三角形,直角三角形,钝角三角形的三条高,并观察高的交点有什么规律?
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
F
画图发现
三角形的三条高交于一点.
(1)锐角三角形的高交于三角形内一点;
(2)直角三角形的高交于直角的顶点;
(3)钝角三角形的高交于三角形外一点.
O
(E,F)
O
三角形的垂心
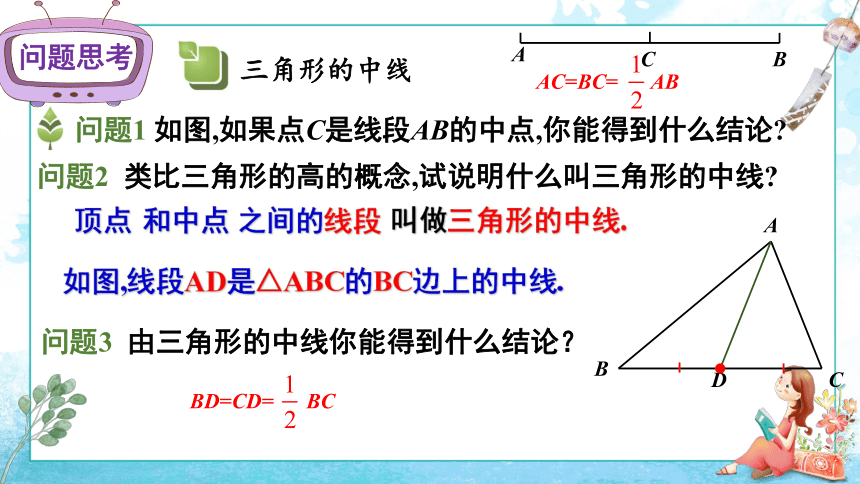
问题1
如图,如果点C是线段AB的中点,你能得到什么结论?
问题思考
顶点
和中点
之间的线段
叫做三角形的中线.
如图,线段AD是△ABC的BC边上的中线.
问题3
由三角形的中线你能得到什么结论?
三角形的中线
A
C
B
AC=BC=
AB
问题2
类比三角形的高的概念,试说明什么叫三角形的中线?
A
B
C
D
BD=CD=
BC
动手操作
问题4
如图,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?为什么?
B
C
D
E
A
答:相等,因为两个三角形等底同高,所以它们面积相等.
问题5
通过问题3你能发现什么规律?
答:三角形的中线能将三角形的面积平分.
动手操作
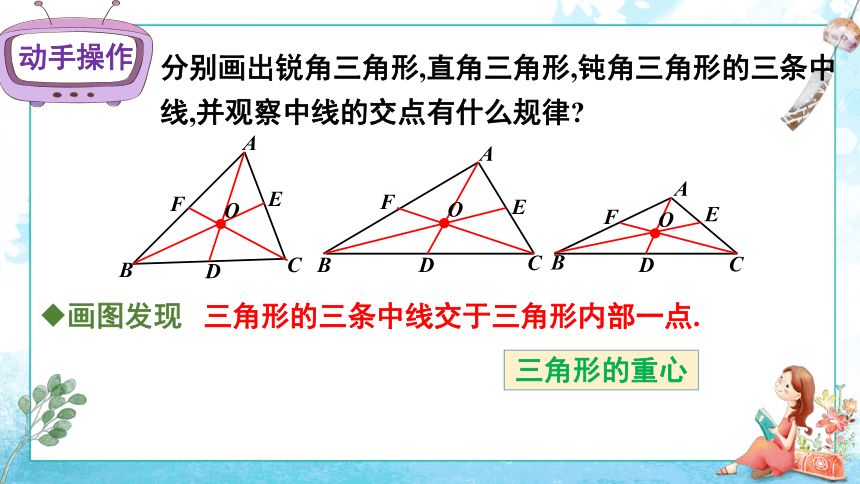
分别画出锐角三角形,直角三角形,钝角三角形的三条中线,并观察中线的交点有什么规律?
画图发现
三角形的三条中线交于三角形内部一点.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
三角形的重心
问题1
如图,若OC是∠AOB的平分线,你能得到什么结论?
问题思考
顶角
和角平分线
之间的线段
叫做三角形的角平分线.
如图,线段AD是△ABC的∠A角平分线.
问题3
由三角形的角平分线你能得到什么结论?
三角形的角平分线
问题2
类比三角形的高的概念,试说明什么叫三角形的角平分线?
∠AOD=
∠COD=
∠AOC
A
C
B
O
∠AOC=
∠BOC
B
C
D
A
(
(
动手操作
类比探索三角形的高和中线的过程,你能得到哪些结论?
画图发现
三角形的三条角平分线交于三角形内部一点.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
想一想:三角形的角平分线与角的角平分线相同吗?为什么?
答:相同点是:平分角;不同点是:前者是线段,后者是射线.
三角形的内心
基础小练
1.如图,在△ABC中,正确画出边AC上的高的是(
)
A.
B.
C.
D.
2.如图,AE是△ABC的中线,EC=4,DE=2,则BD长为(
)
A.2
B.3
C.4
D.6
3.如图,在△ABC中,AD为中线,BE为角平分线,则以下等式:
①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.
其中正确的是(
)
A.①②
B.③④
C.①④
D.②③
基础小练
4.如图,∠1=∠2,∠3=∠4,下列结论中错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.2∠3=∠ACB
D.CE是△ABC的角平分线
5.如图,在△ABC中,∠C=90°,D,E是AC上的两点,
且AE=DE,BD平分∠EBC.那么下列说法中错误的有( )
①BE是△ABD的中线;②BD是△BCE的角平分线;
③∠1=∠2=∠3;④BC是△ABE的高.
A.1个
B.2个
C.3个
D.4个
基础小练
课本P5T2填空:如图(1),AD,BE,CF是△ABC的三条中线,则AB=
2
______,
BD=_____,
AE=
____.
如下页图(2),AD,
BE,
CF是△
ABC的三条角平分线,则∠1=____,
∠3=
_______,
∠ACB=
2_______.
A
B
C
D
E
F
1
2
3
4
A
B
C
D
E
F
课本
P8T4,8
基础小练
7.如图,在△ABC中,已知点E,F分别是AD,CE边上的中点,且S△ABC=8
cm2,则S△BEF的值为______.
8.在△ABC中,CD是中线,已知BC-AC=5cm,
△DBC的周长为25cm,求△ADC的周长.
A
D
B
C
拓展提升
9.如图,已知AD,AE分别是△ABC的中线和高,且AC=5,
AB=3,则△ACD与△ABD的周长之差为_______;
若△ABC的面积为24,则△ACD的面积为______.
A
B
C
D
E
拓展提升
10.如图1,AD,AE分别是△ABC的边BC上的高和中线,已知AD=5,EC=2.
(1)求△ABE和△AEC的面积.
(2)通过做题,你能发现什么结论?请说明理由.
(3)根据(2)中的结论,解决下列问题:如图2,CD是△ABC的中线,DE是△ACD的中线,EF是△ADE的中线,若△AEF的面积为1,求△ABC的面积.
课堂小结
三角形
重要
线段
高
锐角三角形的三条高交于在三角形的内部一点,直角三角形的三条高交于直角顶点,钝角三角形的三条高所在直线交于三角形外部一点→三角形的垂心
中线
三角形的三条中线交于三角形内部一点→三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
三角形的三条角平分线交于三角形内部一点→三角形的内心
三角形
重要
线段
高
中线
角平分线
11.1.2
三角形的高、中线与角平分线
情境引入
P为线段AB上方一点,过点P如何作线段AB的垂线.
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
10
0
1
2
3
4
5
0
1
2
3
4
5
A
B
.P
1.画一个锐角△ABC,过A点向它所对的边BC所在的直线画垂线,垂足为D;
问题思考
A
C
B
●
D
●
顶点
和垂足
之间的线段
叫做三角形的高.
如图,线段AD是△ABC的BC边上的高.
●
●
●
●
●
H
F
E
2.你能画出其他两边上的高吗?
3.由三角形的高你能得到什么结论?
∠ADB=
∠ADC=90
°
三角形的高
动手操作
分别画出锐角三角形,直角三角形,钝角三角形的三条高,并观察高的交点有什么规律?
A
B
C
D
E
F
A
B
C
D
A
B
C
D
E
F
画图发现
三角形的三条高交于一点.
(1)锐角三角形的高交于三角形内一点;
(2)直角三角形的高交于直角的顶点;
(3)钝角三角形的高交于三角形外一点.
O
(E,F)
O
三角形的垂心
问题1
如图,如果点C是线段AB的中点,你能得到什么结论?
问题思考
顶点
和中点
之间的线段
叫做三角形的中线.
如图,线段AD是△ABC的BC边上的中线.
问题3
由三角形的中线你能得到什么结论?
三角形的中线
A
C
B
AC=BC=
AB
问题2
类比三角形的高的概念,试说明什么叫三角形的中线?
A
B
C
D
BD=CD=
BC
动手操作
问题4
如图,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?为什么?
B
C
D
E
A
答:相等,因为两个三角形等底同高,所以它们面积相等.
问题5
通过问题3你能发现什么规律?
答:三角形的中线能将三角形的面积平分.
动手操作
分别画出锐角三角形,直角三角形,钝角三角形的三条中线,并观察中线的交点有什么规律?
画图发现
三角形的三条中线交于三角形内部一点.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
三角形的重心
问题1
如图,若OC是∠AOB的平分线,你能得到什么结论?
问题思考
顶角
和角平分线
之间的线段
叫做三角形的角平分线.
如图,线段AD是△ABC的∠A角平分线.
问题3
由三角形的角平分线你能得到什么结论?
三角形的角平分线
问题2
类比三角形的高的概念,试说明什么叫三角形的角平分线?
∠AOD=
∠COD=
∠AOC
A
C
B
O
∠AOC=
∠BOC
B
C
D
A
(
(
动手操作
类比探索三角形的高和中线的过程,你能得到哪些结论?
画图发现
三角形的三条角平分线交于三角形内部一点.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
想一想:三角形的角平分线与角的角平分线相同吗?为什么?
答:相同点是:平分角;不同点是:前者是线段,后者是射线.
三角形的内心
基础小练
1.如图,在△ABC中,正确画出边AC上的高的是(
)
A.
B.
C.
D.
2.如图,AE是△ABC的中线,EC=4,DE=2,则BD长为(
)
A.2
B.3
C.4
D.6
3.如图,在△ABC中,AD为中线,BE为角平分线,则以下等式:
①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.
其中正确的是(
)
A.①②
B.③④
C.①④
D.②③
基础小练
4.如图,∠1=∠2,∠3=∠4,下列结论中错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.2∠3=∠ACB
D.CE是△ABC的角平分线
5.如图,在△ABC中,∠C=90°,D,E是AC上的两点,
且AE=DE,BD平分∠EBC.那么下列说法中错误的有( )
①BE是△ABD的中线;②BD是△BCE的角平分线;
③∠1=∠2=∠3;④BC是△ABE的高.
A.1个
B.2个
C.3个
D.4个
基础小练
课本P5T2填空:如图(1),AD,BE,CF是△ABC的三条中线,则AB=
2
______,
BD=_____,
AE=
____.
如下页图(2),AD,
BE,
CF是△
ABC的三条角平分线,则∠1=____,
∠3=
_______,
∠ACB=
2_______.
A
B
C
D
E
F
1
2
3
4
A
B
C
D
E
F
课本
P8T4,8
基础小练
7.如图,在△ABC中,已知点E,F分别是AD,CE边上的中点,且S△ABC=8
cm2,则S△BEF的值为______.
8.在△ABC中,CD是中线,已知BC-AC=5cm,
△DBC的周长为25cm,求△ADC的周长.
A
D
B
C
拓展提升
9.如图,已知AD,AE分别是△ABC的中线和高,且AC=5,
AB=3,则△ACD与△ABD的周长之差为_______;
若△ABC的面积为24,则△ACD的面积为______.
A
B
C
D
E
拓展提升
10.如图1,AD,AE分别是△ABC的边BC上的高和中线,已知AD=5,EC=2.
(1)求△ABE和△AEC的面积.
(2)通过做题,你能发现什么结论?请说明理由.
(3)根据(2)中的结论,解决下列问题:如图2,CD是△ABC的中线,DE是△ACD的中线,EF是△ADE的中线,若△AEF的面积为1,求△ABC的面积.
课堂小结
三角形
重要
线段
高
锐角三角形的三条高交于在三角形的内部一点,直角三角形的三条高交于直角顶点,钝角三角形的三条高所在直线交于三角形外部一点→三角形的垂心
中线
三角形的三条中线交于三角形内部一点→三角形的重心
一边上的中线把原三角形分成两个面积相等的三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
三角形的三条角平分线交于三角形内部一点→三角形的内心
三角形
重要
线段
高
中线
角平分线
