22.1.4二次函数y=ax2 bx c的图象和性质(1)课件-人教版九年级数学上册(19张)
文档属性
| 名称 | 22.1.4二次函数y=ax2 bx c的图象和性质(1)课件-人教版九年级数学上册(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 380.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 10:25:19 | ||
图片预览




文档简介
(共19张PPT)
22.1.4
二次函数
y=ax2+bx+c
的图象和性质(1)
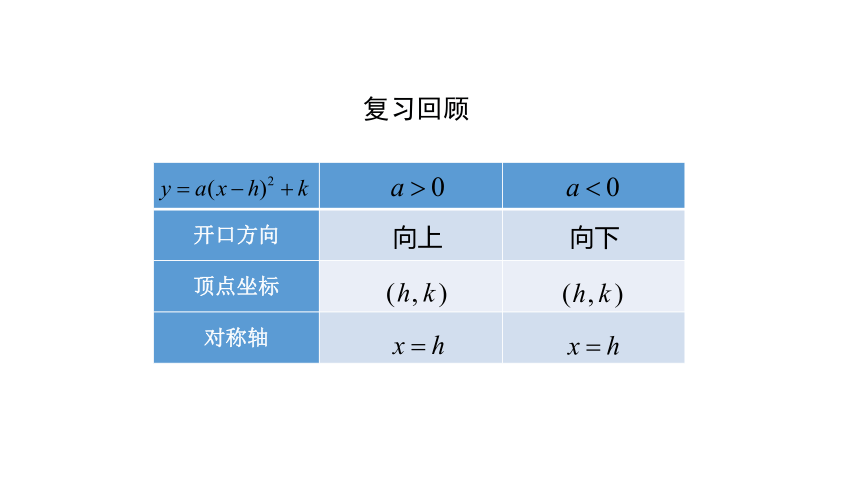
复习回顾
开口方向
顶点坐标
对称轴
向上
向下
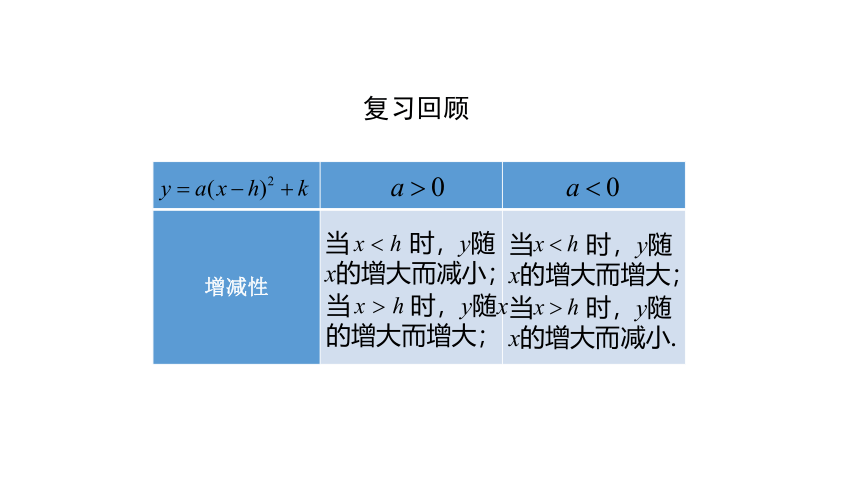
复习回顾
增减性
当
时,y随x的增大而减小;
当
时,y随x的增大而增大;
当
时,y随x的增大而减小.
当
时,y随x的增大而增大;
复习回顾
抛物线
的开口向下,对称轴为
,顶点坐标为
.
当
时,y随x的增大而增大;当
时,
y
随x的增大而减小.
引入新知
想一想:
我们研究过哪些形式的二次函数的图象和性质?
我们如何画出二次函数
的图象?
探究新知
如何把二次函数
转化为
的形式?
解:
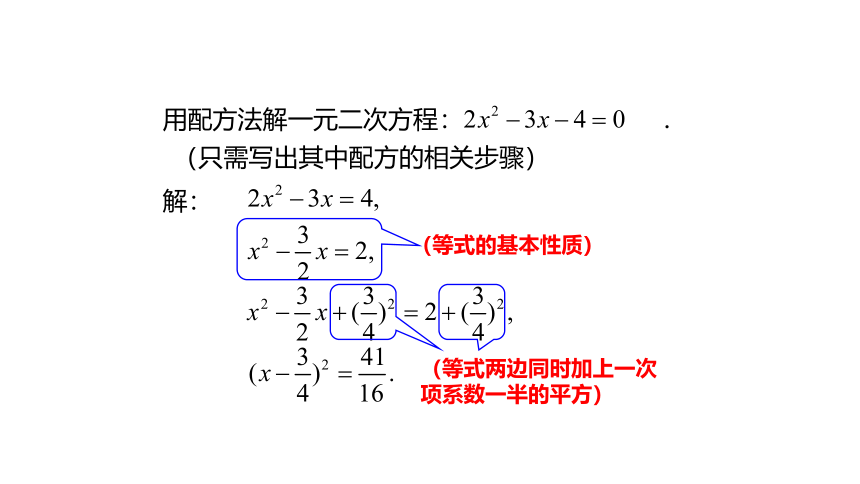
用配方法解一元二次方程:
.
(只需写出其中配方的相关步骤)
(等式的基本性质)
(等式两边同时加上一次项系数一半的平方)
把二次函数
转化为
的形式,并指出抛物线的对称轴和顶点坐标。
解:
(代数式的恒等变形)
把二次函数
转化为
的形式,并指出抛物线的对称轴和顶点坐标.
解:
抛物线的对称轴为
顶点坐标为
练
习
把下列二次函数转化为
的形式,并指出:
抛物线的对称轴和顶点坐标.
(1)
(2)
(1)
解:
抛物线的对称轴为
顶点坐标为
(2)
解:
抛物线的对称轴为
顶点坐标为
想一想
我们能说说抛物线
的对称轴和顶点坐标吗?
解:
抛物线的对称轴为
顶点坐标为
我们能说说抛物线
的对称轴和顶点坐标吗?
解:
另解:
抛物线
的对称轴为
顶点坐标为
我们也可以利用这个结论来求出抛物线的对称轴和顶点坐标。
求抛物线
的对称轴和顶点坐标.
解:
抛物线的对称轴为
抛物线顶点横坐标为
纵坐标为
抛物线
的顶点坐标为
小
结
1.
掌握用配方法把二次函数
转化为
的形式.
2.
体会转化思想.
同学们,再见!
22.1.4
二次函数
y=ax2+bx+c
的图象和性质(1)
复习回顾
开口方向
顶点坐标
对称轴
向上
向下
复习回顾
增减性
当
时,y随x的增大而减小;
当
时,y随x的增大而增大;
当
时,y随x的增大而减小.
当
时,y随x的增大而增大;
复习回顾
抛物线
的开口向下,对称轴为
,顶点坐标为
.
当
时,y随x的增大而增大;当
时,
y
随x的增大而减小.
引入新知
想一想:
我们研究过哪些形式的二次函数的图象和性质?
我们如何画出二次函数
的图象?
探究新知
如何把二次函数
转化为
的形式?
解:
用配方法解一元二次方程:
.
(只需写出其中配方的相关步骤)
(等式的基本性质)
(等式两边同时加上一次项系数一半的平方)
把二次函数
转化为
的形式,并指出抛物线的对称轴和顶点坐标。
解:
(代数式的恒等变形)
把二次函数
转化为
的形式,并指出抛物线的对称轴和顶点坐标.
解:
抛物线的对称轴为
顶点坐标为
练
习
把下列二次函数转化为
的形式,并指出:
抛物线的对称轴和顶点坐标.
(1)
(2)
(1)
解:
抛物线的对称轴为
顶点坐标为
(2)
解:
抛物线的对称轴为
顶点坐标为
想一想
我们能说说抛物线
的对称轴和顶点坐标吗?
解:
抛物线的对称轴为
顶点坐标为
我们能说说抛物线
的对称轴和顶点坐标吗?
解:
另解:
抛物线
的对称轴为
顶点坐标为
我们也可以利用这个结论来求出抛物线的对称轴和顶点坐标。
求抛物线
的对称轴和顶点坐标.
解:
抛物线的对称轴为
抛物线顶点横坐标为
纵坐标为
抛物线
的顶点坐标为
小
结
1.
掌握用配方法把二次函数
转化为
的形式.
2.
体会转化思想.
同学们,再见!
同课章节目录
