23.1图形的旋转(2)课件- 人教版九年级数学上册(68张)
文档属性
| 名称 | 23.1图形的旋转(2)课件- 人教版九年级数学上册(68张) |  | |
| 格式 | zip | ||
| 文件大小 | 11.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 10:25:55 | ||
图片预览







文档简介
(共68张PPT)
23.1
图形的旋转(2)
回顾
旋转的定义:把一个平面图形绕着平面内某一点
O
转动一个角度,叫做图形的旋转.
旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
三种图形变换
平移、
轴对称、
旋转
平移
轴对称
旋转
相同点
平移
轴对称
旋转
相同点
都是全等变换,即变换前后的图形全等.
平移
轴对称
旋转
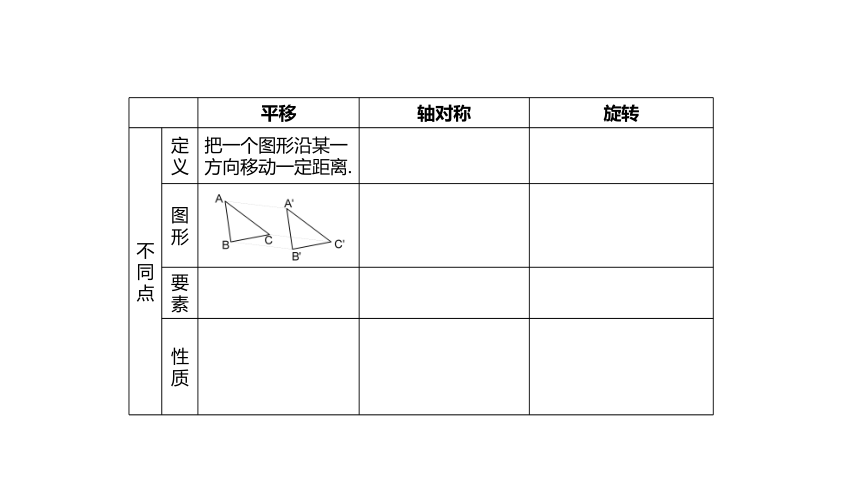
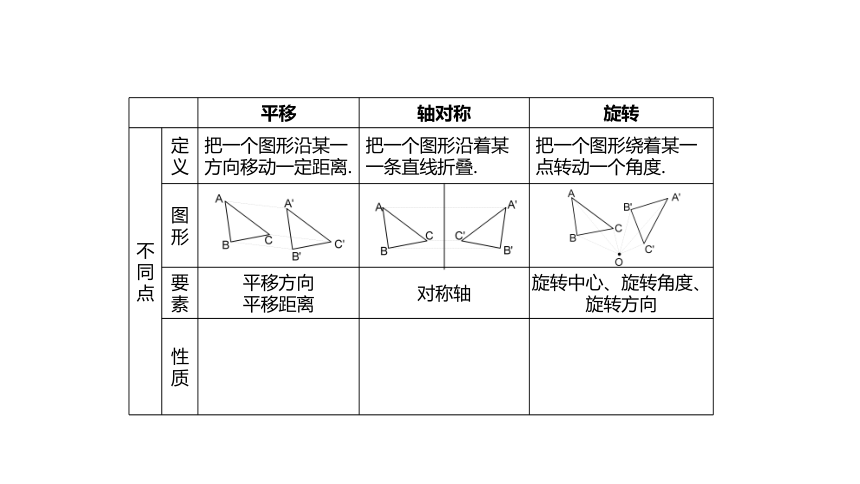
不同点
定义
图形
要素
性质
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
图形
要素
性质
平移
轴对称
旋转
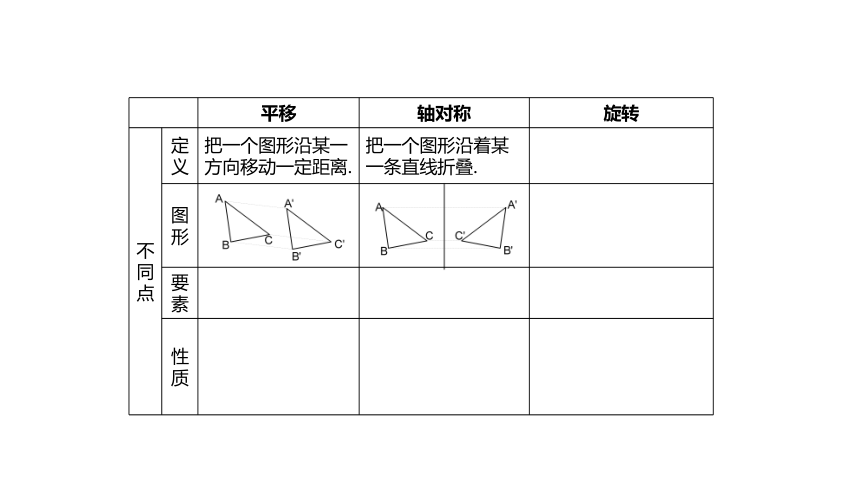
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
图形
要素
性质
平移
轴对称
旋转
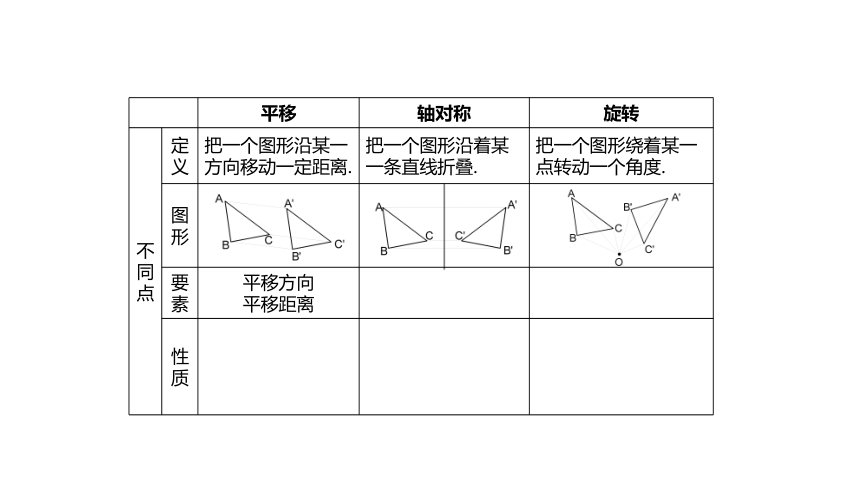
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
性质
平移
轴对称
旋转
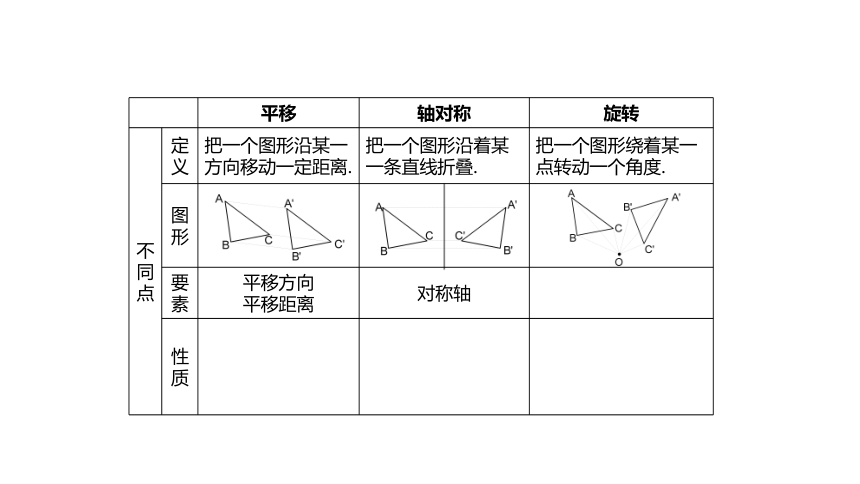
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
性质
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
对称轴
性质
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
对称轴
旋转中心、旋转角度、
旋转方向
性质
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
对称轴
旋转中心、旋转角度、
旋转方向
性质
连接各组对应点的线段平行(或共线)且相等.
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
对称轴
旋转中心、旋转角度、
旋转方向
性质
连接各组对应点的线段平行(或共线)且相等.
任意一对对应点所连线段被对称轴垂直平分.
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
对称轴
旋转中心、旋转角度、
旋转方向
性质
连接各组对应点的线段平行(或共线)且相等.
任意一对对应点所连线段被对称轴垂直平分.
对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.
三种图形变换
轴
对
称
平
移
三种图形变换
轴
对
称
旋
转
三种图形变换
轴对称
旋转
平移
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′,求
EE′
的长.
A
D
E
B
C
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
A
B
C
D
E
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E′
.
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E′
.
在
AE
下方作∠EAM
=
90°,
A
B
C
D
E
M
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E′
.
在
AE
下方作∠EAM
=
90°,在
AM
上
截取
AE′
=
AE,
A
B
C
D
E
M
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E’
.
在
AE
下方作∠EAM
=
90°,在
AM
上
截取
AE′
=
AE,
A
B
C
D
E
M
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E’
.
在
AE
下方作∠EAM
=
90°,在
AM
上
截取
AE′
=
AE,则△ABE′
为旋转后的图形.
A
B
C
D
E
M
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法1:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E′
.
在
AE
下方作∠EAM
=
90°,在
AM
上
截取
AE′
=
AE,则△ABE′
为旋转后的图形.
A
B
C
D
E
M
还有其他方法吗?
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法2:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,BE′
=
DE.
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法2:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,BE′
=
DE.
因此,在
CB
的延长线上取点
E′
,
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法2:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,BE′
=
DE.
因此,在
CB
的延长线上取点
E′
,使
BE′
=
DE,
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法2:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,BE′
=
DE.
因此,在
CB
的延长线上取点
E′
,使
BE′
=
DE,
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法2:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,BE′
=
DE.
因此,在
CB
的延长线上取点
E′
,使
BE′
=
DE,则△ABE′
为旋转后的图形.
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法3:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,AE′
=
AE.
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法3:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,AE′
=
AE.
因此,以点
A为圆心,
AE
为半径画弧,
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法3:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,AE′
=
AE.
因此,以点
A为圆心,
AE
为半径画弧,
和
CB
的延长线的交点即是点
E′
,
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法3:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,AE′
=
AE.
因此,以点
A为圆心,
AE
为半径画弧,
和
CB
的延长线的交点即是点
E′
,则
△ABE′
为旋转后的图形.
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法4:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°.
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法4:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°.
又因为∠EAE′
=
90°,
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法4:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°.
又因为∠EAE′
=
90°,因此,过点
A
作
AE
的垂线与
CB
的延长线的交点即是
点
E′
,
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法4:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°.
又因为∠EAE′
=
90°,因此,过点
A
作
AE
的垂线与
CB
的延长线的交点即是
点
E′
,则△ABE′
为旋转后的图形.
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
A
B
C
D
E
E′
4
3
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
A
B
C
D
E
4
3
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
A
B
C
D
E
4
3
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
A
B
C
D
E
4
3
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
解法1:
在
Rt△ADE
中,AD
=
4,DE
=
3,则
AE
=
5.
因为旋转前后的图形全等,所以
AE′
=
AE
=
5.
A
B
C
D
E
4
3
E′
又因为∠EAE′
=
90°,
所以在
Rt△EAE′
中,EE′
=
.
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
解法2:
A
B
C
D
E
4
3
E′
因此在
Rt△ECE′
中,EC
=
1,E′C
=
7,
则
EE′
=
.
所以
E′
、B、C
三点共线.
∠ABE′
=∠ADE
=
90°,
因为旋转前后的图形全等,所以
BE′
=
DE
=
3,
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
解法2:
因为正方形
ABCD
中,AD
=
4,DE
=
3,所以
EC
=
1,BC
=
4.
A
B
C
D
E
4
3
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
A
D
E
B
C
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
A
D
E
B
C
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
A
D
E
B
C
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
A
D
E
B
C
如果把△ADE
逆时针旋转
90°,
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
A
D
E
B
C
如果把△ADE
逆时针旋转
90°,
此时旋转后的图形是△AD′E′
.
E′
D′
图1
图1
旋转中心不变,旋转角改变
图1
旋转角不变,旋转中心改变
图1
图2
图3
图4
图5
O
O
O
O
旋转对称
一般地,如果一个图形绕着某点
O
旋转角
α
后所得到的图形与原图形重合,则称此图形关于点
O
有角
α
的旋转对称.
旋转对称
一般地,如果一个图形绕着某点
O
旋转角
α
后所得到的图形与原图形重合,则称此图形关于点
O
有角
α
的旋转对称.
小结
小结
对比平移、轴对称、旋转三种图形变换,归纳相同点和不同点.
小结
对比平移、轴对称、旋转三种图形变换,归纳相同点和不同点.
应用旋转的性质,解决问题.
小结
对比平移、轴对称、旋转三种图形变换,归纳相同点和不同点.
应用旋转的性质,解决问题.
借助旋转设计图案.
小结
对比平移、轴对称、旋转三种图形变换,归纳相同点和不同点.
应用旋转的性质,解决问题.
借助旋转设计图案.
旋转对称的概念及其在生活中的广泛应用.
作业
1.
把图中的五角星图案,绕着它的中心
O
旋转.
旋转角至少为多少度时,旋转后的五角星能
与自身重合?对等边三角形进行类似的讨论.
作业
2.
如图,△ABC
中,∠C
=
90°.
(1)将△ABC
绕点
B
逆时针旋转
90°,画出
旋转后的三角形;
(2)若
BC
=
3,AC
=
4,点
A
旋转后的对应
点为
A′,求
A′A
的长.
作业
3.
如图,△ABD,△AEC
都是等边三角形.
BE
与
DC
有什么关系?你能用旋转的性质说明
上述关系成立的理由吗?
同学们,再见!
23.1
图形的旋转(2)
回顾
旋转的定义:把一个平面图形绕着平面内某一点
O
转动一个角度,叫做图形的旋转.
旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
三种图形变换
平移、
轴对称、
旋转
平移
轴对称
旋转
相同点
平移
轴对称
旋转
相同点
都是全等变换,即变换前后的图形全等.
平移
轴对称
旋转
不同点
定义
图形
要素
性质
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
图形
要素
性质
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
图形
要素
性质
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
性质
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
性质
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
对称轴
性质
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
对称轴
旋转中心、旋转角度、
旋转方向
性质
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
对称轴
旋转中心、旋转角度、
旋转方向
性质
连接各组对应点的线段平行(或共线)且相等.
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
对称轴
旋转中心、旋转角度、
旋转方向
性质
连接各组对应点的线段平行(或共线)且相等.
任意一对对应点所连线段被对称轴垂直平分.
平移
轴对称
旋转
不同点
定义
把一个图形沿某一方向移动一定距离.
把一个图形沿着某一条直线折叠.
把一个图形绕着某一点转动一个角度.
图形
要素
平移方向
平移距离
对称轴
旋转中心、旋转角度、
旋转方向
性质
连接各组对应点的线段平行(或共线)且相等.
任意一对对应点所连线段被对称轴垂直平分.
对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.
三种图形变换
轴
对
称
平
移
三种图形变换
轴
对
称
旋
转
三种图形变换
轴对称
旋转
平移
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′,求
EE′
的长.
A
D
E
B
C
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
A
B
C
D
E
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E′
.
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E′
.
在
AE
下方作∠EAM
=
90°,
A
B
C
D
E
M
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E′
.
在
AE
下方作∠EAM
=
90°,在
AM
上
截取
AE′
=
AE,
A
B
C
D
E
M
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E’
.
在
AE
下方作∠EAM
=
90°,在
AM
上
截取
AE′
=
AE,
A
B
C
D
E
M
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
解:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E’
.
在
AE
下方作∠EAM
=
90°,在
AM
上
截取
AE′
=
AE,则△ABE′
为旋转后的图形.
A
B
C
D
E
M
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法1:依题,点
A
的对应点是点
A,点
D
的对应点是点
B
.
设点
E
的对应点为点
E′
.
在
AE
下方作∠EAM
=
90°,在
AM
上
截取
AE′
=
AE,则△ABE′
为旋转后的图形.
A
B
C
D
E
M
还有其他方法吗?
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法2:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,BE′
=
DE.
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法2:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,BE′
=
DE.
因此,在
CB
的延长线上取点
E′
,
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法2:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,BE′
=
DE.
因此,在
CB
的延长线上取点
E′
,使
BE′
=
DE,
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法2:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,BE′
=
DE.
因此,在
CB
的延长线上取点
E′
,使
BE′
=
DE,
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法2:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,BE′
=
DE.
因此,在
CB
的延长线上取点
E′
,使
BE′
=
DE,则△ABE′
为旋转后的图形.
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法3:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,AE′
=
AE.
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法3:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,AE′
=
AE.
因此,以点
A为圆心,
AE
为半径画弧,
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法3:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,AE′
=
AE.
因此,以点
A为圆心,
AE
为半径画弧,
和
CB
的延长线的交点即是点
E′
,
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法3:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°,AE′
=
AE.
因此,以点
A为圆心,
AE
为半径画弧,
和
CB
的延长线的交点即是点
E′
,则
△ABE′
为旋转后的图形.
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法4:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°.
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法4:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°.
又因为∠EAE′
=
90°,
A
B
C
D
E
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法4:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°.
又因为∠EAE′
=
90°,因此,过点
A
作
AE
的垂线与
CB
的延长线的交点即是
点
E′
,
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(1)画出旋转后的图形;
方法4:设点
E
的对应点为点
E′
.
由旋转前后的图形全等,可得∠ABE′
=
∠ADE
=
90°.
又因为∠EAE′
=
90°,因此,过点
A
作
AE
的垂线与
CB
的延长线的交点即是
点
E′
,则△ABE′
为旋转后的图形.
A
B
C
D
E
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
A
B
C
D
E
E′
4
3
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
A
B
C
D
E
4
3
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
A
B
C
D
E
4
3
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
A
B
C
D
E
4
3
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
解法1:
在
Rt△ADE
中,AD
=
4,DE
=
3,则
AE
=
5.
因为旋转前后的图形全等,所以
AE′
=
AE
=
5.
A
B
C
D
E
4
3
E′
又因为∠EAE′
=
90°,
所以在
Rt△EAE′
中,EE′
=
.
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
解法2:
A
B
C
D
E
4
3
E′
因此在
Rt△ECE′
中,EC
=
1,E′C
=
7,
则
EE′
=
.
所以
E′
、B、C
三点共线.
∠ABE′
=∠ADE
=
90°,
因为旋转前后的图形全等,所以
BE′
=
DE
=
3,
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
(2)若
AD
=
4,DE
=
3,点
E
旋转后的对应点为
E′
,求
EE′
的长.
解法2:
因为正方形
ABCD
中,AD
=
4,DE
=
3,所以
EC
=
1,BC
=
4.
A
B
C
D
E
4
3
E′
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
A
D
E
B
C
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
A
D
E
B
C
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
A
D
E
B
C
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
A
D
E
B
C
如果把△ADE
逆时针旋转
90°,
例:如图,E
是正方形
ABCD
中
CD
边上一点,以点
A
为中心,把△ADE
顺时针旋转
90°.
A
D
E
B
C
如果把△ADE
逆时针旋转
90°,
此时旋转后的图形是△AD′E′
.
E′
D′
图1
图1
旋转中心不变,旋转角改变
图1
旋转角不变,旋转中心改变
图1
图2
图3
图4
图5
O
O
O
O
旋转对称
一般地,如果一个图形绕着某点
O
旋转角
α
后所得到的图形与原图形重合,则称此图形关于点
O
有角
α
的旋转对称.
旋转对称
一般地,如果一个图形绕着某点
O
旋转角
α
后所得到的图形与原图形重合,则称此图形关于点
O
有角
α
的旋转对称.
小结
小结
对比平移、轴对称、旋转三种图形变换,归纳相同点和不同点.
小结
对比平移、轴对称、旋转三种图形变换,归纳相同点和不同点.
应用旋转的性质,解决问题.
小结
对比平移、轴对称、旋转三种图形变换,归纳相同点和不同点.
应用旋转的性质,解决问题.
借助旋转设计图案.
小结
对比平移、轴对称、旋转三种图形变换,归纳相同点和不同点.
应用旋转的性质,解决问题.
借助旋转设计图案.
旋转对称的概念及其在生活中的广泛应用.
作业
1.
把图中的五角星图案,绕着它的中心
O
旋转.
旋转角至少为多少度时,旋转后的五角星能
与自身重合?对等边三角形进行类似的讨论.
作业
2.
如图,△ABC
中,∠C
=
90°.
(1)将△ABC
绕点
B
逆时针旋转
90°,画出
旋转后的三角形;
(2)若
BC
=
3,AC
=
4,点
A
旋转后的对应
点为
A′,求
A′A
的长.
作业
3.
如图,△ABD,△AEC
都是等边三角形.
BE
与
DC
有什么关系?你能用旋转的性质说明
上述关系成立的理由吗?
同学们,再见!
同课章节目录
