11.1.1 三角形的边课件-人教版八年级数学上册(34张)
文档属性
| 名称 | 11.1.1 三角形的边课件-人教版八年级数学上册(34张) |  | |
| 格式 | zip | ||
| 文件大小 | 666.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 14:25:34 | ||
图片预览






文档简介
(共34张PPT)
11.1.1
三角形的边
与三角形有关的线段
八年级上册
RJ
初中数学
看一看
想一想
知识回顾
三角形是一种基本的几何图形.从古埃及的金字塔到现代的建筑物,到处都有三角形的形象.为什么在工程建筑、机械制造中经常采用三角形的结构呢?
1.知道三角形的顶点、边、角的表示方法.
2.掌握三角形的三边关系,能利用该关系判断三条线段能否组成三角形.
学习目标
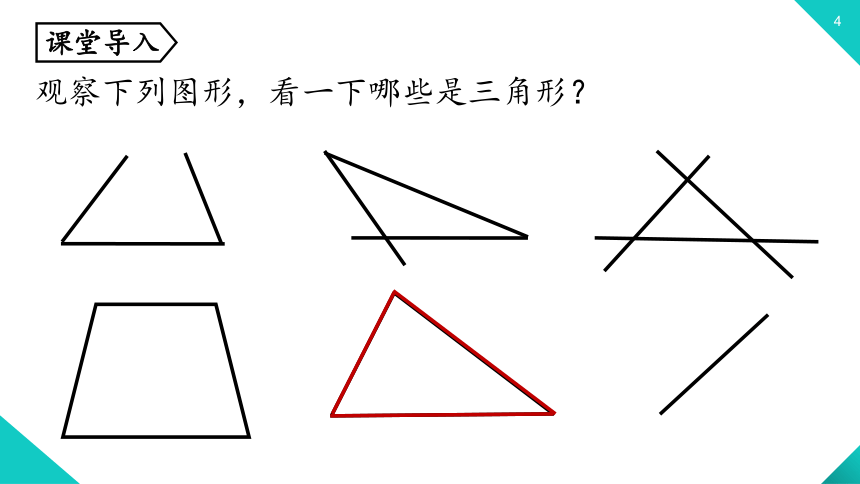
观察下列图形,看一下哪些是三角形?
课堂导入
1.定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
A
B
C
新知探究
知识点1
三角形的有关概念
A
B
C
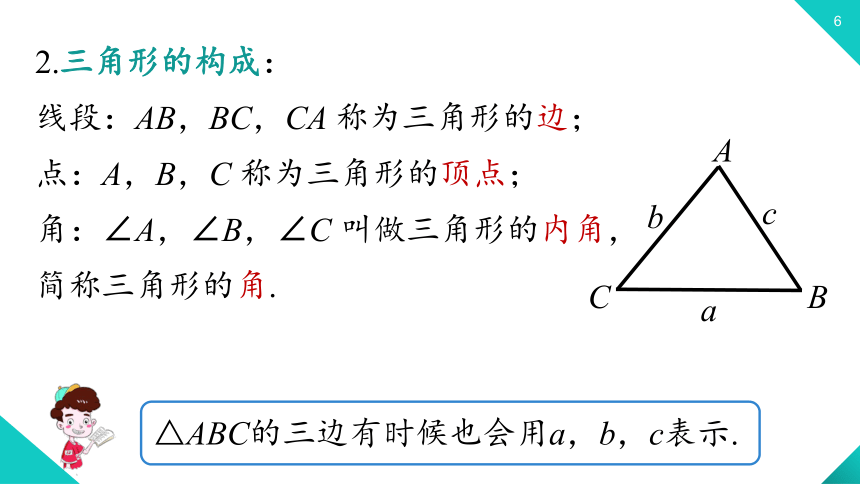
2.三角形的构成:
线段:AB,BC,CA
称为三角形的边;
点:A,B,C
称为三角形的顶点;
角:∠A,∠B,∠C
叫做三角形的内角,简称三角形的角.
△ABC的三边有时候也会用a,b,c表示.
b
a
c
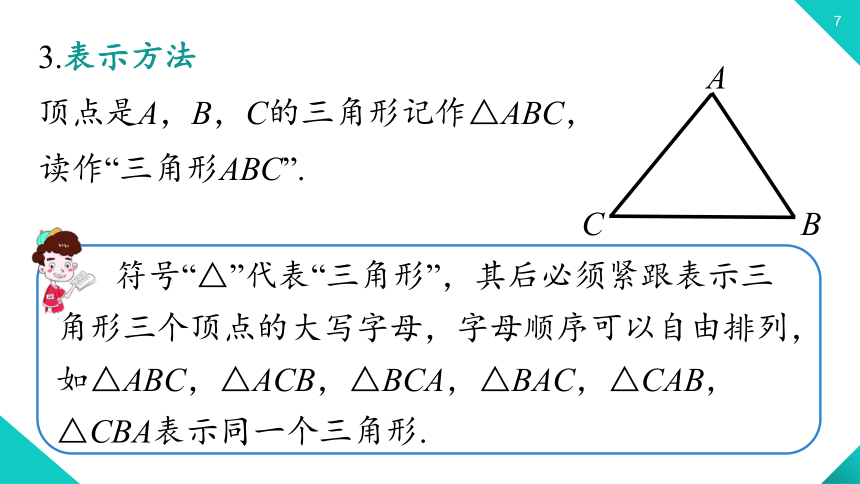
3.表示方法
顶点是A,B,C的三角形记作△ABC,
读作“三角形ABC”.
A
B
C
符号“△”代表“三角形”,其后必须紧跟表示三角形三个顶点的大写字母,字母顺序可以自由排列,如△ABC,△ACB,△BCA,△BAC,△CAB,△CBA表示同一个三角形.
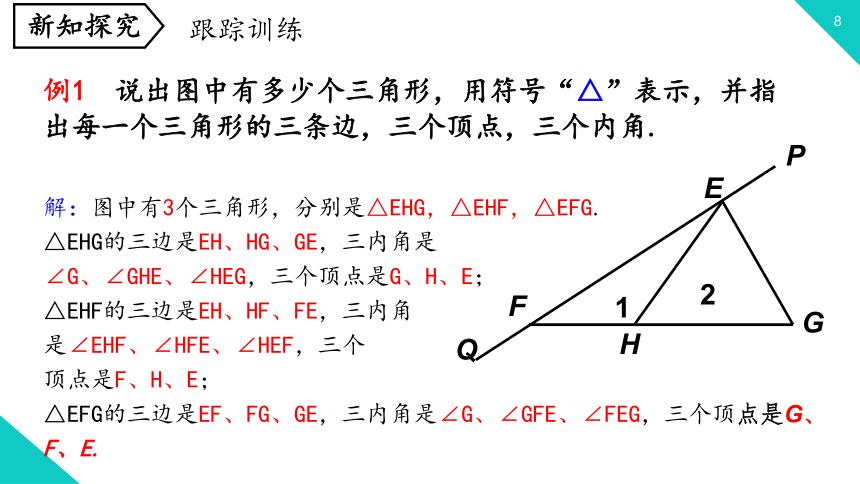
例1
说出图中有多少个三角形,用符号“△”表示,并指出每一个三角形的三条边,三个顶点,三个内角.
解:图中有3个三角形,分别是△EHG,△EHF,△EFG.
△EHG的三边是EH、HG、GE,三内角是
∠G、∠GHE、∠HEG,三个顶点是G、H、E;
△EHF的三边是EH、HF、FE,三内角
是∠EHF、∠HFE、∠HEF,三个
顶点是F、H、E;
△EFG的三边是EF、FG、GE,三内角是∠G、∠GFE、∠FEG,三个顶点是G、F、E.
Q
F
E
P
G
H
1
2
跟踪训练
新知探究
方法点拨
在查三角形的个数时,先给单个三角形编号,查单个的三角形,再查两个三角形组成的较大三角形,然后再查三个,四个三角形组成的三角形.
新知探究
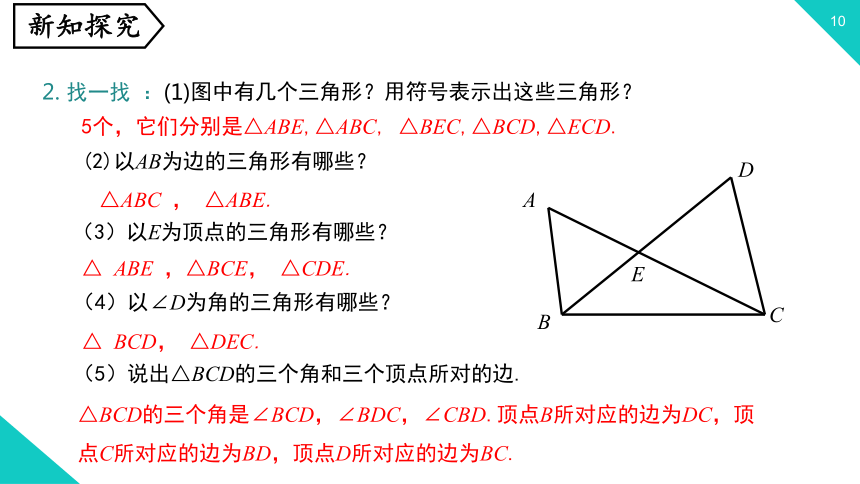
A
B
C
D
E
5个,它们分别是△ABE,△ABC,
△BEC,△BCD,△ECD.
(2)以AB为边的三角形有哪些?
△ABC
,
△ABE.
(3)以E为顶点的三角形有哪些?
△
ABE
,△BCE,
△CDE.
(4)以∠D为角的三角形有哪些?
△
BCD,
△DEC.
(5)说出△BCD的三个角和三个顶点所对的边.
△BCD的三个角是∠BCD,∠BDC,∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.
2.
找一找
:
(
1
)
图
中
有
几
个
三
角
形
?
用
符
号
表
示
出
这
些
三
角
形
?
新知探究
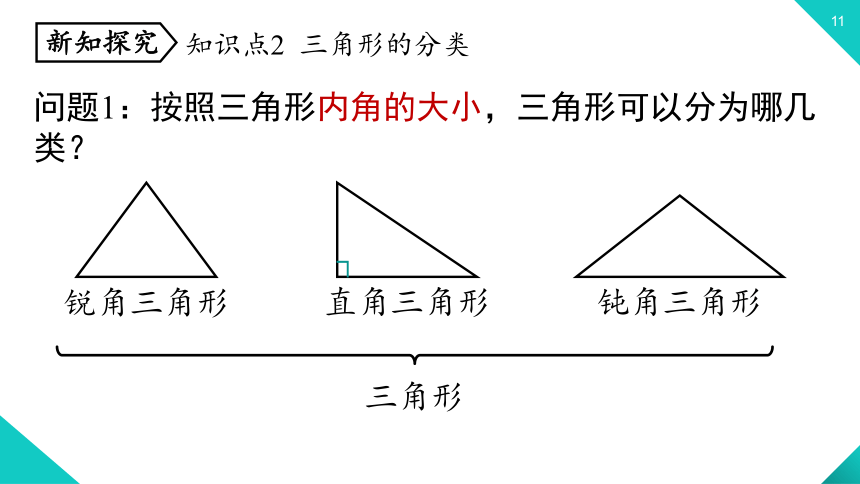
问题1:按照三角形内角的大小,三角形可以分为哪几类?
知识点2
三角形的分类
新知探究
锐角三角形
直角三角形
钝角三角形
三角形
问题2:按照三角形边的相等关系,三角形可以分为哪几类?
A
B
C
三边都相等的三角形
等边三角形
A
B
C
有两条边相等的三角形
等腰三角形
A
B
C
三条边都不相等的三角形
等腰三角形:有两条边相等的三角形叫做等腰三角形,其中相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
等边三角形:三边都相等的三角形叫做等边三角形.
A
B
C
A
腰
腰
顶角
底角
底边
底角
B
C
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形
三边都不相等的三角形
等腰三角形
三角形
底边和腰不相等的等腰三角形
等边三角形
三角形按边的相等关系分类
例2
(1)[2021山西吕梁期中]给出下列说法:①等边三角形是等腰三角形;②三角形按边的相等关系分类可分为等腰三角形、等边三角形和三边都不相等的三角形;③三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形.其中正确的有
( )
A.0个
B.1个
C.2个
D.3个
【解析】 等边三角形是特殊的等腰三角形,故①正确;三角形按边的相等关系分类可分为三边都不相等的三角形和等腰三角形,故②错误;三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形,故③正确.综上,正确的说法有2个.故选C.
新知探究
跟踪训练
(2)
[2021广西河池期中]若△ABC的三边长分别是a,b,c,且(a-b)2+|b-c|=0,则△ABC的形状是 .?
【解析】 因为(a-b)2+|b-c|=0,所以a-b=0且b-c=0,所以a=b且b=c,所以a=b=c,所以△ABC是等边三角形.
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?
路线1:从点B到点A,再从点A到点C,
长度:BA+AC.
A
C
B
知识点3
三角形的三边关系
新知探究
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?
路线2:从点B直接到点C,
长度:BC.
A
C
B
BA+AC
和BC
的大小关系如何?
由“两点之间,线段最短”可知,BA+AC>BC.
路线1:从点C到点B,再从点B到点A,长度:CB+BA.
路线2:从点C直接到点A,长度:CA.
CB+BA和CA的大小关系如何?
由“两点之间,线段最短”
可知,CB+BA>CA.
A
C
B
从点C出发,沿三角形的边到点A,该怎么走?
路线1:从点A到点C,再从点C到点B,长度:AC+CB.
路线2:从点A直接到点B,长度:AB.
AC+CB和AB的大小关系如何?
由“两点之间,线段最短”
可知,AC+CB>AB.
你能得出什么结论?
A
C
B
从点A出发,沿三角形的边到点B,该怎么走?
BA
>
BC-AC
AC+CB
>
AB
BA+AC
>
BC
CB+BA
>
CA
AC
>
AB-CB
CB
>
CA-BA
A
C
B
三角形的三边关系:
1、三角形两边的和大于第三边;
2、三角形两边的差小于第三边.
判断三条线段能否组成三角形,只需判断“两条较短的线段之和大于第三条”即可.
三角形三边关系中的“两边”是指任意两边,判断三条线段能否组成三角形是否一定要检验三条线段中任意两条线段的和都大于第三条,有没有更简便的方法?
(1)不能,因为3cm+4cm<8cm,不符合三角形两边
的和大于第三边.
(2)不能,因为5cm+6cm=11cm,不符合三角形两边的和大于第三边.
(3)能,因为4cm+7cm>9cm,符合三角形两边的和大于第三边.
例3
判断下列长度的三条线段能否组成三角形?为什么?
(1)
3cm,8cm,4cm
(2)
5cm,6cm,11cm
(3)
4cm,7cm,9cm
跟踪训练
新知探究
解:
例4
用一条长为18
cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
解:(1)设底边长为x
cm,则腰长为2x
cm.
由题可得:
x+2x+2x=18,
解得x=3.6.
所以,三边长分别为3.6
cm,7.2
cm,7.2
cm.
(2)因为长为4cm的边可能是腰,也可能是底边,所以需要分情况讨论.
如果4
cm长的边为底边,设腰长为x
cm,
则4+x+x=18,解得x=7.
如果4
cm长的边为腰,设底边长为xcm,
则4+4+x=18,解得x=10.
解答完成了吗?
(2)能围成有一边的长是4
cm的等腰三角形吗?为什么?
因为4+4<10,不符合三角形两边的和大于第三边,
所以不能围成腰长是4
cm的等腰三角形.
由以上讨论可知,可以围成底边是4
cm的等腰三角形.
针对每种情况,验证所求出的三边长是否满足三角形的三边关系,不满足的要舍去.
1.
图中有几个三角形,用符号表示这些三角形.
解:共有6个三角形,分别是:
△ABD,△ABE,△ABC,
△ADE,△ADC,△AEC.
随堂练习
A
B
C
D
E
2.
一个等腰三角形的一边长为6cm,周长为20cm,求其他两边的长.
解:分两种情况进行讨论:
(1)当腰长为6cm的时候,底边长为20-6-6=8(cm),
则该等腰三角形的另外两边长分别为6cm,8cm.
(2)当底边长为6cm的时候,腰长为(20-6)÷2=7(cm),
则该等腰三角形的另外两边分别为7
cm,7
cm.
概念
三角形
三角形的分类
三角形的三边关系
按角分类
按边分类
三角形两边的和
大于第三边
三角形两边的差
小于第三边
边、顶点、角
课堂小结
拓展提升
1.(2020?绍兴中考)长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为(
)
A.4
B.5
C.6
D.7
解:
分类
围法
能否构成三角形
理由
情况1
2+3,3,4
能
3+4>5
情况2
2,3+3,4
否
2+4=6
情况3
2,3,3+4
否
2+3<7
情况4
2+4,3,3
否
3+3=6
由表格分析可知得到的三角形的最长边长为5.
B
2.
(1)已知等腰三角形的一边长为5,一边长为6,求它的周长.
解:(1)当腰长为5时,底边为6,三条边的长分别为5,5,6,因为5+5>6,所以能组成三角形,三角形的周长为5+5+6=16;
当腰长为6时,底边为5,三条边的长分别为6,6,5,因为6+5>6,所以能组成三角形,三角形的周长为6+6+5=17.
综上,此三角形的周长为16或17.
2.
(2)已知等腰三角形的一边长为4,一边长为9,求它的周长.
解:(2)当腰长为4时,底边为9,三条边的长分别为4,4,9,因为4+4<9,所以不能组成三角形;
当腰长为9时,底边为4,三条边的长分别为9,9,4,因为4+9>9,所以能组成三角形,三角形的周长为9+9+4=22.
3.[2020吉林长春期末]将一个三角形纸片剪成两个三角形,这两个三角形不可能
( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
【解析】 如图1,得到的两个三角形都是直角三角形;如图2,得到的两个三角形都是钝角三角形;如图3,得到的两个三角形是一个直角三角形和一个钝角三角形.故选C.
C
4.
[2021河南濮阳期末]若实数m,n满足等式|m-2|+=0,
且m,n恰好是等腰三角形ABC两条边的长,则△ABC的周长为 .?
【解析】 ∵|m-2|+=0,∴m-2=0,n-4=0,∴m=2,n=4.分情况讨论:
①若腰长为2,底边长为4,因为2+2=4,不符合三角形的三边关系,所以此种情况不成立;
②若腰长为4,底边长为2,因为2+4>4,符合三角形的三边关系,所以能组成三角形,
此时△ABC的周长为4+4+2=10.综上,△ABC的周长为10.
11.1.1
三角形的边
与三角形有关的线段
八年级上册
RJ
初中数学
看一看
想一想
知识回顾
三角形是一种基本的几何图形.从古埃及的金字塔到现代的建筑物,到处都有三角形的形象.为什么在工程建筑、机械制造中经常采用三角形的结构呢?
1.知道三角形的顶点、边、角的表示方法.
2.掌握三角形的三边关系,能利用该关系判断三条线段能否组成三角形.
学习目标
观察下列图形,看一下哪些是三角形?
课堂导入
1.定义:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
A
B
C
新知探究
知识点1
三角形的有关概念
A
B
C
2.三角形的构成:
线段:AB,BC,CA
称为三角形的边;
点:A,B,C
称为三角形的顶点;
角:∠A,∠B,∠C
叫做三角形的内角,简称三角形的角.
△ABC的三边有时候也会用a,b,c表示.
b
a
c
3.表示方法
顶点是A,B,C的三角形记作△ABC,
读作“三角形ABC”.
A
B
C
符号“△”代表“三角形”,其后必须紧跟表示三角形三个顶点的大写字母,字母顺序可以自由排列,如△ABC,△ACB,△BCA,△BAC,△CAB,△CBA表示同一个三角形.
例1
说出图中有多少个三角形,用符号“△”表示,并指出每一个三角形的三条边,三个顶点,三个内角.
解:图中有3个三角形,分别是△EHG,△EHF,△EFG.
△EHG的三边是EH、HG、GE,三内角是
∠G、∠GHE、∠HEG,三个顶点是G、H、E;
△EHF的三边是EH、HF、FE,三内角
是∠EHF、∠HFE、∠HEF,三个
顶点是F、H、E;
△EFG的三边是EF、FG、GE,三内角是∠G、∠GFE、∠FEG,三个顶点是G、F、E.
Q
F
E
P
G
H
1
2
跟踪训练
新知探究
方法点拨
在查三角形的个数时,先给单个三角形编号,查单个的三角形,再查两个三角形组成的较大三角形,然后再查三个,四个三角形组成的三角形.
新知探究
A
B
C
D
E
5个,它们分别是△ABE,△ABC,
△BEC,△BCD,△ECD.
(2)以AB为边的三角形有哪些?
△ABC
,
△ABE.
(3)以E为顶点的三角形有哪些?
△
ABE
,△BCE,
△CDE.
(4)以∠D为角的三角形有哪些?
△
BCD,
△DEC.
(5)说出△BCD的三个角和三个顶点所对的边.
△BCD的三个角是∠BCD,∠BDC,∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.
2.
找一找
:
(
1
)
图
中
有
几
个
三
角
形
?
用
符
号
表
示
出
这
些
三
角
形
?
新知探究
问题1:按照三角形内角的大小,三角形可以分为哪几类?
知识点2
三角形的分类
新知探究
锐角三角形
直角三角形
钝角三角形
三角形
问题2:按照三角形边的相等关系,三角形可以分为哪几类?
A
B
C
三边都相等的三角形
等边三角形
A
B
C
有两条边相等的三角形
等腰三角形
A
B
C
三条边都不相等的三角形
等腰三角形:有两条边相等的三角形叫做等腰三角形,其中相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
等边三角形:三边都相等的三角形叫做等边三角形.
A
B
C
A
腰
腰
顶角
底角
底边
底角
B
C
等边三角形是特殊的等腰三角形,即底边和腰相等的等腰三角形
三边都不相等的三角形
等腰三角形
三角形
底边和腰不相等的等腰三角形
等边三角形
三角形按边的相等关系分类
例2
(1)[2021山西吕梁期中]给出下列说法:①等边三角形是等腰三角形;②三角形按边的相等关系分类可分为等腰三角形、等边三角形和三边都不相等的三角形;③三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形.其中正确的有
( )
A.0个
B.1个
C.2个
D.3个
【解析】 等边三角形是特殊的等腰三角形,故①正确;三角形按边的相等关系分类可分为三边都不相等的三角形和等腰三角形,故②错误;三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形,故③正确.综上,正确的说法有2个.故选C.
新知探究
跟踪训练
(2)
[2021广西河池期中]若△ABC的三边长分别是a,b,c,且(a-b)2+|b-c|=0,则△ABC的形状是 .?
【解析】 因为(a-b)2+|b-c|=0,所以a-b=0且b-c=0,所以a=b且b=c,所以a=b=c,所以△ABC是等边三角形.
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?
路线1:从点B到点A,再从点A到点C,
长度:BA+AC.
A
C
B
知识点3
三角形的三边关系
新知探究
任意画一个△ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?各条线路的长有什么关系?
路线2:从点B直接到点C,
长度:BC.
A
C
B
BA+AC
和BC
的大小关系如何?
由“两点之间,线段最短”可知,BA+AC>BC.
路线1:从点C到点B,再从点B到点A,长度:CB+BA.
路线2:从点C直接到点A,长度:CA.
CB+BA和CA的大小关系如何?
由“两点之间,线段最短”
可知,CB+BA>CA.
A
C
B
从点C出发,沿三角形的边到点A,该怎么走?
路线1:从点A到点C,再从点C到点B,长度:AC+CB.
路线2:从点A直接到点B,长度:AB.
AC+CB和AB的大小关系如何?
由“两点之间,线段最短”
可知,AC+CB>AB.
你能得出什么结论?
A
C
B
从点A出发,沿三角形的边到点B,该怎么走?
BA
>
BC-AC
AC+CB
>
AB
BA+AC
>
BC
CB+BA
>
CA
AC
>
AB-CB
CB
>
CA-BA
A
C
B
三角形的三边关系:
1、三角形两边的和大于第三边;
2、三角形两边的差小于第三边.
判断三条线段能否组成三角形,只需判断“两条较短的线段之和大于第三条”即可.
三角形三边关系中的“两边”是指任意两边,判断三条线段能否组成三角形是否一定要检验三条线段中任意两条线段的和都大于第三条,有没有更简便的方法?
(1)不能,因为3cm+4cm<8cm,不符合三角形两边
的和大于第三边.
(2)不能,因为5cm+6cm=11cm,不符合三角形两边的和大于第三边.
(3)能,因为4cm+7cm>9cm,符合三角形两边的和大于第三边.
例3
判断下列长度的三条线段能否组成三角形?为什么?
(1)
3cm,8cm,4cm
(2)
5cm,6cm,11cm
(3)
4cm,7cm,9cm
跟踪训练
新知探究
解:
例4
用一条长为18
cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
解:(1)设底边长为x
cm,则腰长为2x
cm.
由题可得:
x+2x+2x=18,
解得x=3.6.
所以,三边长分别为3.6
cm,7.2
cm,7.2
cm.
(2)因为长为4cm的边可能是腰,也可能是底边,所以需要分情况讨论.
如果4
cm长的边为底边,设腰长为x
cm,
则4+x+x=18,解得x=7.
如果4
cm长的边为腰,设底边长为xcm,
则4+4+x=18,解得x=10.
解答完成了吗?
(2)能围成有一边的长是4
cm的等腰三角形吗?为什么?
因为4+4<10,不符合三角形两边的和大于第三边,
所以不能围成腰长是4
cm的等腰三角形.
由以上讨论可知,可以围成底边是4
cm的等腰三角形.
针对每种情况,验证所求出的三边长是否满足三角形的三边关系,不满足的要舍去.
1.
图中有几个三角形,用符号表示这些三角形.
解:共有6个三角形,分别是:
△ABD,△ABE,△ABC,
△ADE,△ADC,△AEC.
随堂练习
A
B
C
D
E
2.
一个等腰三角形的一边长为6cm,周长为20cm,求其他两边的长.
解:分两种情况进行讨论:
(1)当腰长为6cm的时候,底边长为20-6-6=8(cm),
则该等腰三角形的另外两边长分别为6cm,8cm.
(2)当底边长为6cm的时候,腰长为(20-6)÷2=7(cm),
则该等腰三角形的另外两边分别为7
cm,7
cm.
概念
三角形
三角形的分类
三角形的三边关系
按角分类
按边分类
三角形两边的和
大于第三边
三角形两边的差
小于第三边
边、顶点、角
课堂小结
拓展提升
1.(2020?绍兴中考)长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为(
)
A.4
B.5
C.6
D.7
解:
分类
围法
能否构成三角形
理由
情况1
2+3,3,4
能
3+4>5
情况2
2,3+3,4
否
2+4=6
情况3
2,3,3+4
否
2+3<7
情况4
2+4,3,3
否
3+3=6
由表格分析可知得到的三角形的最长边长为5.
B
2.
(1)已知等腰三角形的一边长为5,一边长为6,求它的周长.
解:(1)当腰长为5时,底边为6,三条边的长分别为5,5,6,因为5+5>6,所以能组成三角形,三角形的周长为5+5+6=16;
当腰长为6时,底边为5,三条边的长分别为6,6,5,因为6+5>6,所以能组成三角形,三角形的周长为6+6+5=17.
综上,此三角形的周长为16或17.
2.
(2)已知等腰三角形的一边长为4,一边长为9,求它的周长.
解:(2)当腰长为4时,底边为9,三条边的长分别为4,4,9,因为4+4<9,所以不能组成三角形;
当腰长为9时,底边为4,三条边的长分别为9,9,4,因为4+9>9,所以能组成三角形,三角形的周长为9+9+4=22.
3.[2020吉林长春期末]将一个三角形纸片剪成两个三角形,这两个三角形不可能
( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
【解析】 如图1,得到的两个三角形都是直角三角形;如图2,得到的两个三角形都是钝角三角形;如图3,得到的两个三角形是一个直角三角形和一个钝角三角形.故选C.
C
4.
[2021河南濮阳期末]若实数m,n满足等式|m-2|+=0,
且m,n恰好是等腰三角形ABC两条边的长,则△ABC的周长为 .?
【解析】 ∵|m-2|+=0,∴m-2=0,n-4=0,∴m=2,n=4.分情况讨论:
①若腰长为2,底边长为4,因为2+2=4,不符合三角形的三边关系,所以此种情况不成立;
②若腰长为4,底边长为2,因为2+4>4,符合三角形的三边关系,所以能组成三角形,
此时△ABC的周长为4+4+2=10.综上,△ABC的周长为10.
