2020-2021学年山东省烟台市招远市七年级(下)期中数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省烟台市招远市七年级(下)期中数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-05 00:00:00 | ||
图片预览



文档简介
2020-2021学年山东省烟台市招远市七年级(下)期中数学试卷(五四学制)
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.下列成语描述的事件为随机事件的是( )
A.缘木求鱼 B.水落石出 C.瓮中捉鳖 D.守株待兔
2.给出下列命题:
(1)三角形的一个外角一定大于它的一个内角
(2)若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形
(3)三角形的最小内角不能大于60°
(4)三角形的一个外角等于和它不相邻的两个内角的和
其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
3.用加减法解方程组时,下列变形正确的是( )
A. B.
C. D.
4.下列说法正确的是( )
A.篮球队员在罚球线上投篮一次,则“投中”是随机事件
B.明天的降水概率为40%,则“明天下雨”是确定事件
C.任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件
D.a是实数,则“|a|≥0”是不可能事件
5.如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
A.数形结合 B.特殊到一般 C.一般到特殊 D.转化
6.若方程组的解满足x+y=2021,则k等于( )
A.2019 B.2020 C.2021 D.2022
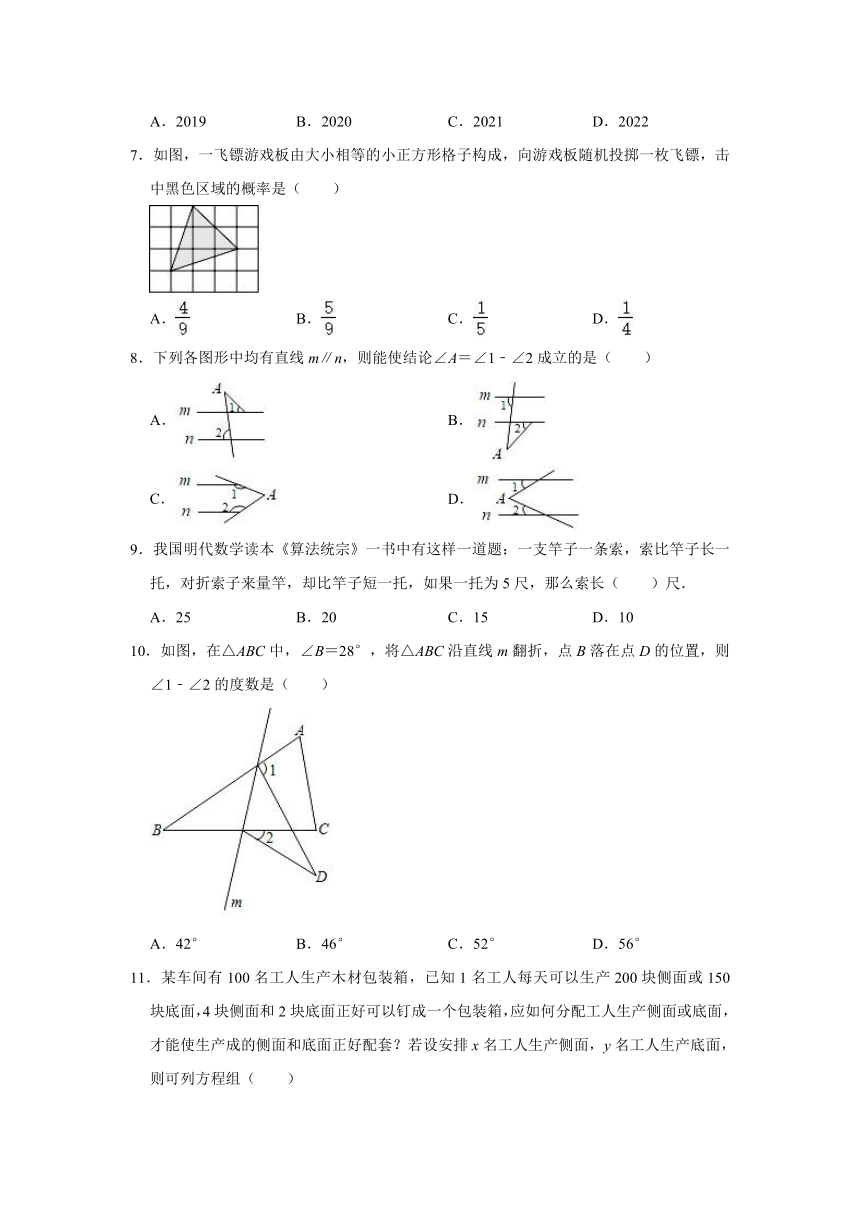
7.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是( )
A. B. C. D.
8.下列各图形中均有直线m∥n,则能使结论∠A=∠1﹣∠2成立的是( )
A. B.
C. D.
9.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为5尺,那么索长( )尺.
A.25 B.20 C.15 D.10
10.如图,在△ABC中,∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.42° B.46° C.52° D.56°
11.某车间有100名工人生产木材包装箱,已知1名工人每天可以生产200块侧面或150块底面,4块侧面和2块底面正好可以钉成一个包装箱,应如何分配工人生产侧面或底面,才能使生产成的侧面和底面正好配套?若设安排x名工人生产侧面,y名工人生产底面,则可列方程组( )
A. B.
C. D.
12.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.小东认为:任意抛掷一个啤酒盖,啤酒盖落地后印有商标一面向上的可能性的大小是,你认为小东的想法 (“合理”或“不合理”).
14.如图,将一副三角板如图摆放,则图中∠1的度数是 度.
15.如图,在同一直角坐标系中作出一次函数y=k1x与y=k2x+b的图象,则二元一次方程组的解是 .
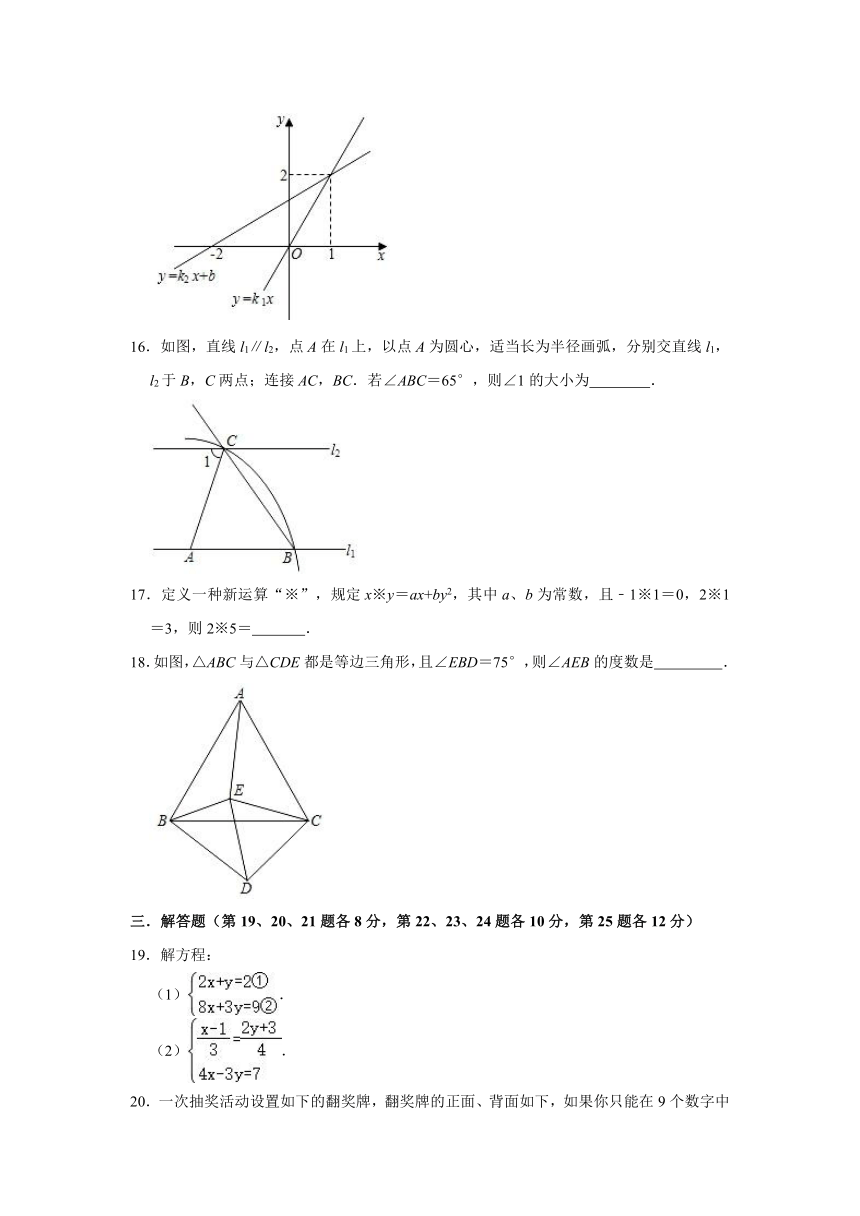
16.如图,直线l1∥l2,点A在l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点;连接AC,BC.若∠ABC=65°,则∠1的大小为 .
17.定义一种新运算“※”,规定x※y=ax+by2,其中a、b为常数,且﹣1※1=0,2※1=3,则2※5= .
18.如图,△ABC与△CDE都是等边三角形,且∠EBD=75°,则∠AEB的度数是 .
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.解方程:
(1).
(2).
20.一次抽奖活动设置如下的翻奖牌,翻奖牌的正面、背面如下,如果你只能在9个数字中选中一个翻牌,请解决下面的问题:
(1)直接写出抽到“手机”奖品的可能性的大小;
(2)每个奖牌只能翻一次,翻过的奖牌不能再翻.若第一次没有抽到“手机”奖品,请求出第二次抽到“手机”奖品的可能性的大小;
(3)请你根据题意设计翻奖牌反面的奖品,包含(手机、微波炉、球拍、电影票,谢谢参与)使得最后抽到“球拍”的可能性大小是.
21.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
22.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x﹣4交于D,C为直线CD与y轴的交点,求:
(1)直线AB对应的函数表达式;
(2)求S△ADC.
23.金都百货电器商场销售进价分别为120元、190元的A、B两种型号的电风扇,第一批货两周销售完毕,如表所示是近二周的销售情况(进价、售价均保持不变,利润=销售收入﹣进货成本):
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 5 7 2570
第二周 8 9 3540
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场再购进这两种型号的电风扇共120台,并且全部销售完,该商场能否实现这两批电风扇的总利润为8310元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
24.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(2)如图3,在(1)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=3:5,BE平分∠ABG,求∠CBG的度数.
25.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
参考答案
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.下列成语描述的事件为随机事件的是( )
A.缘木求鱼 B.水落石出 C.瓮中捉鳖 D.守株待兔
【分析】根据事件发生的可能性大小判断,得到答案.
解:A、缘木求鱼,是不可能事件;
B、水落石出,是必然事件;
C、瓮中捉鳖,是必然事件;
D、守株待兔,是随机事件;
故选:D.
2.给出下列命题:
(1)三角形的一个外角一定大于它的一个内角
(2)若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形
(3)三角形的最小内角不能大于60°
(4)三角形的一个外角等于和它不相邻的两个内角的和
其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】据三角形的外角的性质和三角形内角和定理对各个选项进行判断即可.
解:(1)三角形的一个外角不一定大于它的一个内角,故错误;
(2)若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形,故正确;
(3)三角形的最小内角不能大于60°,故正确,
(4)三角形的一个外角等于和它不相邻的两个内角的和,故正确.
故选:C.
3.用加减法解方程组时,下列变形正确的是( )
A. B.
C. D.
【分析】观察两方程中y的系数特征,即可得到结果.
解:用加减法解方程组时,变形为:,
故选:B.
4.下列说法正确的是( )
A.篮球队员在罚球线上投篮一次,则“投中”是随机事件
B.明天的降水概率为40%,则“明天下雨”是确定事件
C.任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件
D.a是实数,则“|a|≥0”是不可能事件
【分析】根据概率的意义、随机事件和必然事件及不可能事件的概念逐一判断即可得.
解:A.篮球队员在罚球线上投篮一次,则“投中”是随机事件,此选项正确;
B.明天的降水概率为40%,则“明天下雨”是随机事件,此选项错误;
C.任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是随机事件,此选项错误;
D.a是实数,则“|a|≥0”是必然事件,此选项错误;
故选:A.
5.如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
A.数形结合 B.特殊到一般 C.一般到特殊 D.转化
【分析】根据三角形内角和定理的证明过程,可寻找到转化的解题思想,此题得解.
【解答】证明:∵∠ABC=∠ECD,∠BAC=∠ACE,∠BCD=∠BCA+∠ACE+∠ECD=180°,
∴∠BCA+∠BAC+∠ABC=180°.
此方法中用到了替换,体现了转化的思想.
故选:D.
6.若方程组的解满足x+y=2021,则k等于( )
A.2019 B.2020 C.2021 D.2022
【分析】以k为已知数解方程组,将方程组的解代入方程x+y=2021,即可求得k的值.
解:.
①×2﹣②×3得:
﹣25y=﹣5k.
∴y=k.
将y=k代入①得:
x=﹣1.
∴.
将代入x+y=2021中得:
.
∴k=2022.
故选:D.
7.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是( )
A. B. C. D.
【分析】利用黑色区域的面积除以游戏板的面积即可.
解:黑色区域的面积=3×3﹣×3×1﹣×2×2﹣×3×1=4,
所以击中黑色区域的概率==.
故选:C.
8.下列各图形中均有直线m∥n,则能使结论∠A=∠1﹣∠2成立的是( )
A. B.
C. D.
【分析】根据平行线的性质解答即可.
解:A、∵m∥n,
∴∠2=∠1+∠A,
∴∠A=∠2﹣∠1,不符合题意;
B、∵m∥n,
∴∠1=∠2+∠A,
∴∠A=∠1﹣∠2,符合题意;
C、∵m∥n,
∴∠1+∠2+∠A=360°,
∴∠A=360°﹣∠2﹣∠1,不符合题意;
D、∵m∥n,
∴∠A=∠1+∠2,不符合题意;
故选:B.
9.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为5尺,那么索长( )尺.
A.25 B.20 C.15 D.10
【分析】设索长x尺,竿子长y尺,根据“索比竿子长一托,对折索子来量竿,却比竿子短一托”,即可得出关于x,y的二元一次方程组,解之即可得出结论.
解:设索长x尺,竿子长y尺,
依题意,得:,
解得:.
故选:B.
10.如图,在△ABC中,∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.42° B.46° C.52° D.56°
【分析】根据折叠得出∠D=∠B=28°,根据三角形的外角性质得出∠1=∠B+∠BEF,∠BEF=∠2+∠D,求出∠1=∠B+∠2+∠D即可.
解:
∵∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,
∴∠D=∠B=28°,
∵∠1=∠B+∠BEF,∠BEF=∠2+∠D,
∴∠1=∠B+∠2+∠D,
∴∠1﹣∠2=∠B+∠D=28°+28°=56°,
故选:D.
11.某车间有100名工人生产木材包装箱,已知1名工人每天可以生产200块侧面或150块底面,4块侧面和2块底面正好可以钉成一个包装箱,应如何分配工人生产侧面或底面,才能使生产成的侧面和底面正好配套?若设安排x名工人生产侧面,y名工人生产底面,则可列方程组( )
A. B.
C. D.
【分析】设安排x名工人生产侧面,y名工人生产底面,才能使做成的侧面和底面正好配套,根据2个底面和4个侧面(2大2小)可以做成一个包装箱,列出方程组,即可解答;
解:设安排x名工人生产侧面,y名工人生产底面,才能使做成的侧面和底面正好配套,可得:,
故选:C.
12.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【分析】①由AD平分△ABC的外角∠EAC,求出∠EAD=∠DAC,由三角形外角得∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,得出∠EAD=∠ABC,利用同位角相等两直线平行得出结论正确.
②由AD∥BC,得出∠ADB=∠DBC,再由BD平分∠ABC,所以∠ABD=∠DBC,∠ABC=2∠ADB,得出结论∠ACB=2∠ADB,
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,利用角的关系得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,得出结论∠ADC=90°﹣∠ABD;④由∠BAC+∠ABC=∠ACF,得出∠BAC+∠ABC=∠ACF,再与∠BDC+∠DBC=∠ACF相结合,得出∠BAC=∠BDC,即∠BDC=∠BAC.
解:①∵AD平分△ABC的外角∠EAC,
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故①正确.
②由(1)可知AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故②正确.
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°﹣∠ABD,
故③正确;
④∵∠BAC+∠ABC=∠ACF,
∴∠BAC+∠ABC=∠ACF,
∵∠BDC+∠DBC=∠ACF,
∴∠BAC+∠ABC=∠BDC+∠DBC,
∵∠DBC=∠ABC,
∴∠BAC=∠BDC,即∠BDC=∠BAC.
故④错误.
故选:C.
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.小东认为:任意抛掷一个啤酒盖,啤酒盖落地后印有商标一面向上的可能性的大小是,你认为小东的想法 不合理 (“合理”或“不合理”).
【分析】根据啤酒盖的正反两面不均匀,抛掷后向上一面的两种可能:印有商标一面向上、印有商标一面向下的可能性不一样,据此解答可得.
解:小东的想法不合理,
理由:啤酒盖的正反两面不均匀,抛掷后向上一面的两种可能:印有商标一面向上、印有商标一面向下的可能性不一样,
所以小东的想法不合理,
故答案为:不合理.
14.如图,将一副三角板如图摆放,则图中∠1的度数是 105 度.
【分析】根据三角形的外角性求出∠2,根据补角的概念求出∠1.
解:由三角形的外角性质控可知,∠2=30°+45°=75°,
∴∠1=180°﹣∠2=105°,
故答案为:105.
15.如图,在同一直角坐标系中作出一次函数y=k1x与y=k2x+b的图象,则二元一次方程组的解是 .
【分析】一次函数图象的交点就是两函数组成的方程组的解.
解:∵一次函数y=k1x与y=k2x+b的图象交于点(1,2),
∴二元一次方程组的解是,
故答案为:.
16.如图,直线l1∥l2,点A在l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点;连接AC,BC.若∠ABC=65°,则∠1的大小为 50° .
【分析】根据等腰三角形性质求出∠ACB,根据三角形的内角和定理求出∠CAB,根据平行线性质求出即可.
解:∵AC=AB,
∴∠ACB=∠ABC=65°,
根据三角形的内角和定理得:∠ACB+∠ABC+∠CAB=180°,
∴∠CAB=180°﹣∠ACB﹣∠ABC=180°﹣65°﹣65°=50°,
∵l1∥l2,
∴∠1=∠CAB=50°,
故答案为:50°.
17.定义一种新运算“※”,规定x※y=ax+by2,其中a、b为常数,且﹣1※1=0,2※1=3,则2※5= 27 .
【分析】根据已知条件得出,求出方程组的解,再求出答案即可.
解:∵﹣1※1=0,2※1=3,
∴,
②﹣①,得3a=3,
解得:a=1,
把a=1代入①,得﹣1+b=0,
解得:b=1,
∴2※5=2×1+1×52=27,
故答案为:27.
18.如图,△ABC与△CDE都是等边三角形,且∠EBD=75°,则∠AEB的度数是 135° .
【分析】根据等边三角形性质得出AC=BC,CE=CD,∠BAC=60°,∠ACB=∠ECD=60°,求出∠ACE=∠BCD,证△ACE≌△BCD,根据全等三角形的性质得出∠CAE=∠CBD,求出∠ABE+∠BAE=45°,根据三角形内角和定理求出即可.
解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CE=CD,∠BAC=60°,∠ACB=∠ECD=60°,
∴∠ACB﹣∠ECB=∠ECD﹣∠ECB,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵∠EBD=75°,
∴75°﹣∠EBC=60°﹣∠BAE,
∴75°﹣(60°﹣∠ABE)=60°﹣∠BAE,
∴∠ABE+∠BAE=45°,
∴∠AEB=180°﹣(∠ABE+∠BAE)=135°.
故答案为:135°.
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.解方程:
(1).
(2).
【分析】(1)②﹣①×3得出2x=3,求出x,把x=代入①求出y即可;
(2)整理后②﹣①得出3y=﹣6,求出y,把y=﹣2代入②求出x即可.
解:(1),
②﹣①×3得:2x=3,
解得:x=,
把x=代入①得:3+y=2,
解得:y=﹣1,
所以原方程组的解为:;
(2)整理,得
②﹣①得:3y=﹣6,
解得:y=﹣2,
把y=﹣2代入②得:4x﹣3×(﹣2)=7,
解得:x=,
所以原方程的解为:.
20.一次抽奖活动设置如下的翻奖牌,翻奖牌的正面、背面如下,如果你只能在9个数字中选中一个翻牌,请解决下面的问题:
(1)直接写出抽到“手机”奖品的可能性的大小;
(2)每个奖牌只能翻一次,翻过的奖牌不能再翻.若第一次没有抽到“手机”奖品,请求出第二次抽到“手机”奖品的可能性的大小;
(3)请你根据题意设计翻奖牌反面的奖品,包含(手机、微波炉、球拍、电影票,谢谢参与)使得最后抽到“球拍”的可能性大小是.
【分析】(1)用“手机”的数量除以总数量即可;
(2)第二次的抽取机会一共有8种可能,第二次抽到“手机”奖品的结果有2种,根据概率公式求解即可;
(3)根据概率公式求解即可.
解:(1)由图可得,抽到“手机”奖品的可能性是:;
(2)由题意可得,第二次的抽取机会一共有8种可能,第二次抽到“手机”奖品的结果有2种,
即第二次抽到“手机”奖品的可能性是==;
(3)设计九张牌中有四张写着球拍,其它的五张牌中手机、微波炉、电影票各一张,谢谢参与两张.(答案不唯一).
21.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
【分析】(1)根据平行线的判定和性质定理即可得到结论;
(2)根据三角形的内角和定理即可得到结论.
【解答】(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,
∴AB∥EF,
∴∠B=∠EFC,
∴∠ADE=∠EFC;
(2)解:∵∠ACB=72°,∠A=60°,
∴∠B=180°﹣∠A﹣∠ACB=48°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB=180°﹣90°﹣48°=42°.
22.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x﹣4交于D,C为直线CD与y轴的交点,求:
(1)直线AB对应的函数表达式;
(2)求S△ADC.
【分析】(1)根据待定系数法即可求得;
(2)由y=x﹣4求得C的坐标,解析式联立,解方程组求得D的坐标,然后根据三角形面积公式即可求得.
解:(1)设直线AB的解析式为y=kx+b,
把A(0,2),B(3,0)分别代入,
得,解得,
所以直线AB的解析式为y=﹣x+2;
(2)过点D作DM⊥y轴,垂足为M,
∵y=x﹣4,
∴当x=0时,y=﹣4,则C(0,﹣4),
解方程组,得,
则D(6,﹣2),
∴DM=6,
∵C(0,﹣4),A(0,2),
∴AC=6,
所以S△ADC=AC?DM=×6×6=18.
23.金都百货电器商场销售进价分别为120元、190元的A、B两种型号的电风扇,第一批货两周销售完毕,如表所示是近二周的销售情况(进价、售价均保持不变,利润=销售收入﹣进货成本):
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 5 7 2570
第二周 8 9 3540
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场再购进这两种型号的电风扇共120台,并且全部销售完,该商场能否实现这两批电风扇的总利润为8310元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【分析】(1)设A种型号的电风扇的销售单价为x元/台,B种型号的电风扇的销售单价为y元/台,由题意列出方程组,可求解;
(2)设再购进A种型号的电风扇m台,则购进B种型号的电风扇(120﹣m)台,由总利润为8310元,列出方程可求解.
解:(1)设A种型号的电风扇的销售单价为x元/台,B种型号的电风扇的销售单价为y元/台,
依题意得:,
解得:,
答:A种型号的电风扇的销售单价为150元/台,B种型号的电风扇的销售单价为260元/台.
(2)设再购进A种型号的电风扇m台,则购进B种型号的电风扇(120﹣m)台,
依题意,得:(150﹣120)(5+8+m)+(260﹣190)(120﹣m+7+9)=8310,
解得:m=40,
∴120﹣m=80.
答:再购进A种型号的电风扇40台,B种型号的电风扇80台,就能实现这两批电风扇的总利润为8310元的目标.
24.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(2)如图3,在(1)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=3:5,BE平分∠ABG,求∠CBG的度数.
【分析】(1)如图2,过点E作EK∥AB,可得CF∥AB∥EK,再根据平行线的性质即可得结论;
(2)根据∠EBC:∠ECB=3:5,可以设∠EBC=3x°,则∠ECB=5x°,然后根据∠AED+∠DEB+∠BEC=180°,3x+5x+100=180,求出x的值,进而可得结果.
解:(1)过点E作EK∥AB,
∵DE∥BC,
∴∠ADE=∠ABC,
∵∠BCF+∠ADE=180°,
∴∠BCF+∠ABC=180°,
∴CF∥AB,
∵EK∥AB,
∴CF∥EK,∠BEK=∠ABE=40°,
∴∠CEK=∠ACF=60°,
∴∠BEC=∠BEK+∠CEK=40°+60°=100°;
(2)∵BE平分∠ABG,
∴∠EBG=∠ABE=40°,
∵∠EBC:∠ECB=3:5,
∴设∠EBC=3x°,则∠ECB=5x°,
∵DE∥BC,
∴∠DEB=∠EBC=3x°,∠AED=∠ECB=5x°,
∵∠AED+∠DEB+∠BEC=180°,
∴3x+5x+100=180,
解得x=10,
∴∠EBC=3x°=30°,
∴∠CBG=∠EBG﹣∠EBC=40°﹣30°=10°.
25.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
【分析】(1)根据函数图象中的数据,可以得到货车的速度和轿车到达乙地的时间,然后即可计算出轿车到达乙地时,货车与甲地的距离;
(2)根据函数图象中的数据,可以得到线段CD对应的函数表达式;
(3)根据题意和函数图象中的数据,可以计算出在轿车行进过程,轿车行驶多少时间,两车相距15千米.
解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.下列成语描述的事件为随机事件的是( )
A.缘木求鱼 B.水落石出 C.瓮中捉鳖 D.守株待兔
2.给出下列命题:
(1)三角形的一个外角一定大于它的一个内角
(2)若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形
(3)三角形的最小内角不能大于60°
(4)三角形的一个外角等于和它不相邻的两个内角的和
其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
3.用加减法解方程组时,下列变形正确的是( )
A. B.
C. D.
4.下列说法正确的是( )
A.篮球队员在罚球线上投篮一次,则“投中”是随机事件
B.明天的降水概率为40%,则“明天下雨”是确定事件
C.任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件
D.a是实数,则“|a|≥0”是不可能事件
5.如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
A.数形结合 B.特殊到一般 C.一般到特殊 D.转化
6.若方程组的解满足x+y=2021,则k等于( )
A.2019 B.2020 C.2021 D.2022
7.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是( )
A. B. C. D.
8.下列各图形中均有直线m∥n,则能使结论∠A=∠1﹣∠2成立的是( )
A. B.
C. D.
9.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为5尺,那么索长( )尺.
A.25 B.20 C.15 D.10
10.如图,在△ABC中,∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.42° B.46° C.52° D.56°
11.某车间有100名工人生产木材包装箱,已知1名工人每天可以生产200块侧面或150块底面,4块侧面和2块底面正好可以钉成一个包装箱,应如何分配工人生产侧面或底面,才能使生产成的侧面和底面正好配套?若设安排x名工人生产侧面,y名工人生产底面,则可列方程组( )
A. B.
C. D.
12.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.小东认为:任意抛掷一个啤酒盖,啤酒盖落地后印有商标一面向上的可能性的大小是,你认为小东的想法 (“合理”或“不合理”).
14.如图,将一副三角板如图摆放,则图中∠1的度数是 度.
15.如图,在同一直角坐标系中作出一次函数y=k1x与y=k2x+b的图象,则二元一次方程组的解是 .
16.如图,直线l1∥l2,点A在l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点;连接AC,BC.若∠ABC=65°,则∠1的大小为 .
17.定义一种新运算“※”,规定x※y=ax+by2,其中a、b为常数,且﹣1※1=0,2※1=3,则2※5= .
18.如图,△ABC与△CDE都是等边三角形,且∠EBD=75°,则∠AEB的度数是 .
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.解方程:
(1).
(2).
20.一次抽奖活动设置如下的翻奖牌,翻奖牌的正面、背面如下,如果你只能在9个数字中选中一个翻牌,请解决下面的问题:
(1)直接写出抽到“手机”奖品的可能性的大小;
(2)每个奖牌只能翻一次,翻过的奖牌不能再翻.若第一次没有抽到“手机”奖品,请求出第二次抽到“手机”奖品的可能性的大小;
(3)请你根据题意设计翻奖牌反面的奖品,包含(手机、微波炉、球拍、电影票,谢谢参与)使得最后抽到“球拍”的可能性大小是.
21.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
22.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x﹣4交于D,C为直线CD与y轴的交点,求:
(1)直线AB对应的函数表达式;
(2)求S△ADC.
23.金都百货电器商场销售进价分别为120元、190元的A、B两种型号的电风扇,第一批货两周销售完毕,如表所示是近二周的销售情况(进价、售价均保持不变,利润=销售收入﹣进货成本):
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 5 7 2570
第二周 8 9 3540
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场再购进这两种型号的电风扇共120台,并且全部销售完,该商场能否实现这两批电风扇的总利润为8310元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
24.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(2)如图3,在(1)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=3:5,BE平分∠ABG,求∠CBG的度数.
25.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
参考答案
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.下列成语描述的事件为随机事件的是( )
A.缘木求鱼 B.水落石出 C.瓮中捉鳖 D.守株待兔
【分析】根据事件发生的可能性大小判断,得到答案.
解:A、缘木求鱼,是不可能事件;
B、水落石出,是必然事件;
C、瓮中捉鳖,是必然事件;
D、守株待兔,是随机事件;
故选:D.
2.给出下列命题:
(1)三角形的一个外角一定大于它的一个内角
(2)若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形
(3)三角形的最小内角不能大于60°
(4)三角形的一个外角等于和它不相邻的两个内角的和
其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】据三角形的外角的性质和三角形内角和定理对各个选项进行判断即可.
解:(1)三角形的一个外角不一定大于它的一个内角,故错误;
(2)若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形,故正确;
(3)三角形的最小内角不能大于60°,故正确,
(4)三角形的一个外角等于和它不相邻的两个内角的和,故正确.
故选:C.
3.用加减法解方程组时,下列变形正确的是( )
A. B.
C. D.
【分析】观察两方程中y的系数特征,即可得到结果.
解:用加减法解方程组时,变形为:,
故选:B.
4.下列说法正确的是( )
A.篮球队员在罚球线上投篮一次,则“投中”是随机事件
B.明天的降水概率为40%,则“明天下雨”是确定事件
C.任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是必然事件
D.a是实数,则“|a|≥0”是不可能事件
【分析】根据概率的意义、随机事件和必然事件及不可能事件的概念逐一判断即可得.
解:A.篮球队员在罚球线上投篮一次,则“投中”是随机事件,此选项正确;
B.明天的降水概率为40%,则“明天下雨”是随机事件,此选项错误;
C.任意抛掷一枚质地均匀的硬币10次,则“5次正面朝上”是随机事件,此选项错误;
D.a是实数,则“|a|≥0”是必然事件,此选项错误;
故选:A.
5.如图,在证明“△ABC内角和等于180°”时,延长BC至D,过点C作CE∥AB,得到∠ABC=∠ECD,∠BAC=∠ACE,由于∠BCD=180°,可得到∠ABC+∠ACB+∠BAC=180°,这个证明方法体现的数学思想是( )
A.数形结合 B.特殊到一般 C.一般到特殊 D.转化
【分析】根据三角形内角和定理的证明过程,可寻找到转化的解题思想,此题得解.
【解答】证明:∵∠ABC=∠ECD,∠BAC=∠ACE,∠BCD=∠BCA+∠ACE+∠ECD=180°,
∴∠BCA+∠BAC+∠ABC=180°.
此方法中用到了替换,体现了转化的思想.
故选:D.
6.若方程组的解满足x+y=2021,则k等于( )
A.2019 B.2020 C.2021 D.2022
【分析】以k为已知数解方程组,将方程组的解代入方程x+y=2021,即可求得k的值.
解:.
①×2﹣②×3得:
﹣25y=﹣5k.
∴y=k.
将y=k代入①得:
x=﹣1.
∴.
将代入x+y=2021中得:
.
∴k=2022.
故选:D.
7.如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是( )
A. B. C. D.
【分析】利用黑色区域的面积除以游戏板的面积即可.
解:黑色区域的面积=3×3﹣×3×1﹣×2×2﹣×3×1=4,
所以击中黑色区域的概率==.
故选:C.
8.下列各图形中均有直线m∥n,则能使结论∠A=∠1﹣∠2成立的是( )
A. B.
C. D.
【分析】根据平行线的性质解答即可.
解:A、∵m∥n,
∴∠2=∠1+∠A,
∴∠A=∠2﹣∠1,不符合题意;
B、∵m∥n,
∴∠1=∠2+∠A,
∴∠A=∠1﹣∠2,符合题意;
C、∵m∥n,
∴∠1+∠2+∠A=360°,
∴∠A=360°﹣∠2﹣∠1,不符合题意;
D、∵m∥n,
∴∠A=∠1+∠2,不符合题意;
故选:B.
9.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为5尺,那么索长( )尺.
A.25 B.20 C.15 D.10
【分析】设索长x尺,竿子长y尺,根据“索比竿子长一托,对折索子来量竿,却比竿子短一托”,即可得出关于x,y的二元一次方程组,解之即可得出结论.
解:设索长x尺,竿子长y尺,
依题意,得:,
解得:.
故选:B.
10.如图,在△ABC中,∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.42° B.46° C.52° D.56°
【分析】根据折叠得出∠D=∠B=28°,根据三角形的外角性质得出∠1=∠B+∠BEF,∠BEF=∠2+∠D,求出∠1=∠B+∠2+∠D即可.
解:
∵∠B=28°,将△ABC沿直线m翻折,点B落在点D的位置,
∴∠D=∠B=28°,
∵∠1=∠B+∠BEF,∠BEF=∠2+∠D,
∴∠1=∠B+∠2+∠D,
∴∠1﹣∠2=∠B+∠D=28°+28°=56°,
故选:D.
11.某车间有100名工人生产木材包装箱,已知1名工人每天可以生产200块侧面或150块底面,4块侧面和2块底面正好可以钉成一个包装箱,应如何分配工人生产侧面或底面,才能使生产成的侧面和底面正好配套?若设安排x名工人生产侧面,y名工人生产底面,则可列方程组( )
A. B.
C. D.
【分析】设安排x名工人生产侧面,y名工人生产底面,才能使做成的侧面和底面正好配套,根据2个底面和4个侧面(2大2小)可以做成一个包装箱,列出方程组,即可解答;
解:设安排x名工人生产侧面,y名工人生产底面,才能使做成的侧面和底面正好配套,可得:,
故选:C.
12.如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【分析】①由AD平分△ABC的外角∠EAC,求出∠EAD=∠DAC,由三角形外角得∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,得出∠EAD=∠ABC,利用同位角相等两直线平行得出结论正确.
②由AD∥BC,得出∠ADB=∠DBC,再由BD平分∠ABC,所以∠ABD=∠DBC,∠ABC=2∠ADB,得出结论∠ACB=2∠ADB,
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,利用角的关系得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,得出结论∠ADC=90°﹣∠ABD;④由∠BAC+∠ABC=∠ACF,得出∠BAC+∠ABC=∠ACF,再与∠BDC+∠DBC=∠ACF相结合,得出∠BAC=∠BDC,即∠BDC=∠BAC.
解:①∵AD平分△ABC的外角∠EAC,
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故①正确.
②由(1)可知AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故②正确.
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°﹣∠ABD,
故③正确;
④∵∠BAC+∠ABC=∠ACF,
∴∠BAC+∠ABC=∠ACF,
∵∠BDC+∠DBC=∠ACF,
∴∠BAC+∠ABC=∠BDC+∠DBC,
∵∠DBC=∠ABC,
∴∠BAC=∠BDC,即∠BDC=∠BAC.
故④错误.
故选:C.
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.小东认为:任意抛掷一个啤酒盖,啤酒盖落地后印有商标一面向上的可能性的大小是,你认为小东的想法 不合理 (“合理”或“不合理”).
【分析】根据啤酒盖的正反两面不均匀,抛掷后向上一面的两种可能:印有商标一面向上、印有商标一面向下的可能性不一样,据此解答可得.
解:小东的想法不合理,
理由:啤酒盖的正反两面不均匀,抛掷后向上一面的两种可能:印有商标一面向上、印有商标一面向下的可能性不一样,
所以小东的想法不合理,
故答案为:不合理.
14.如图,将一副三角板如图摆放,则图中∠1的度数是 105 度.
【分析】根据三角形的外角性求出∠2,根据补角的概念求出∠1.
解:由三角形的外角性质控可知,∠2=30°+45°=75°,
∴∠1=180°﹣∠2=105°,
故答案为:105.
15.如图,在同一直角坐标系中作出一次函数y=k1x与y=k2x+b的图象,则二元一次方程组的解是 .
【分析】一次函数图象的交点就是两函数组成的方程组的解.
解:∵一次函数y=k1x与y=k2x+b的图象交于点(1,2),
∴二元一次方程组的解是,
故答案为:.
16.如图,直线l1∥l2,点A在l1上,以点A为圆心,适当长为半径画弧,分别交直线l1,l2于B,C两点;连接AC,BC.若∠ABC=65°,则∠1的大小为 50° .
【分析】根据等腰三角形性质求出∠ACB,根据三角形的内角和定理求出∠CAB,根据平行线性质求出即可.
解:∵AC=AB,
∴∠ACB=∠ABC=65°,
根据三角形的内角和定理得:∠ACB+∠ABC+∠CAB=180°,
∴∠CAB=180°﹣∠ACB﹣∠ABC=180°﹣65°﹣65°=50°,
∵l1∥l2,
∴∠1=∠CAB=50°,
故答案为:50°.
17.定义一种新运算“※”,规定x※y=ax+by2,其中a、b为常数,且﹣1※1=0,2※1=3,则2※5= 27 .
【分析】根据已知条件得出,求出方程组的解,再求出答案即可.
解:∵﹣1※1=0,2※1=3,
∴,
②﹣①,得3a=3,
解得:a=1,
把a=1代入①,得﹣1+b=0,
解得:b=1,
∴2※5=2×1+1×52=27,
故答案为:27.
18.如图,△ABC与△CDE都是等边三角形,且∠EBD=75°,则∠AEB的度数是 135° .
【分析】根据等边三角形性质得出AC=BC,CE=CD,∠BAC=60°,∠ACB=∠ECD=60°,求出∠ACE=∠BCD,证△ACE≌△BCD,根据全等三角形的性质得出∠CAE=∠CBD,求出∠ABE+∠BAE=45°,根据三角形内角和定理求出即可.
解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CE=CD,∠BAC=60°,∠ACB=∠ECD=60°,
∴∠ACB﹣∠ECB=∠ECD﹣∠ECB,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵∠EBD=75°,
∴75°﹣∠EBC=60°﹣∠BAE,
∴75°﹣(60°﹣∠ABE)=60°﹣∠BAE,
∴∠ABE+∠BAE=45°,
∴∠AEB=180°﹣(∠ABE+∠BAE)=135°.
故答案为:135°.
三.解答题(第19、20、21题各8分,第22、23、24题各10分,第25题各12分)
19.解方程:
(1).
(2).
【分析】(1)②﹣①×3得出2x=3,求出x,把x=代入①求出y即可;
(2)整理后②﹣①得出3y=﹣6,求出y,把y=﹣2代入②求出x即可.
解:(1),
②﹣①×3得:2x=3,
解得:x=,
把x=代入①得:3+y=2,
解得:y=﹣1,
所以原方程组的解为:;
(2)整理,得
②﹣①得:3y=﹣6,
解得:y=﹣2,
把y=﹣2代入②得:4x﹣3×(﹣2)=7,
解得:x=,
所以原方程的解为:.
20.一次抽奖活动设置如下的翻奖牌,翻奖牌的正面、背面如下,如果你只能在9个数字中选中一个翻牌,请解决下面的问题:
(1)直接写出抽到“手机”奖品的可能性的大小;
(2)每个奖牌只能翻一次,翻过的奖牌不能再翻.若第一次没有抽到“手机”奖品,请求出第二次抽到“手机”奖品的可能性的大小;
(3)请你根据题意设计翻奖牌反面的奖品,包含(手机、微波炉、球拍、电影票,谢谢参与)使得最后抽到“球拍”的可能性大小是.
【分析】(1)用“手机”的数量除以总数量即可;
(2)第二次的抽取机会一共有8种可能,第二次抽到“手机”奖品的结果有2种,根据概率公式求解即可;
(3)根据概率公式求解即可.
解:(1)由图可得,抽到“手机”奖品的可能性是:;
(2)由题意可得,第二次的抽取机会一共有8种可能,第二次抽到“手机”奖品的结果有2种,
即第二次抽到“手机”奖品的可能性是==;
(3)设计九张牌中有四张写着球拍,其它的五张牌中手机、微波炉、电影票各一张,谢谢参与两张.(答案不唯一).
21.如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
【分析】(1)根据平行线的判定和性质定理即可得到结论;
(2)根据三角形的内角和定理即可得到结论.
【解答】(1)证明:∵DE∥BC,
∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,
∴AB∥EF,
∴∠B=∠EFC,
∴∠ADE=∠EFC;
(2)解:∵∠ACB=72°,∠A=60°,
∴∠B=180°﹣∠A﹣∠ACB=48°,
∵CD⊥AB,
∴∠BDC=90°,
∴∠DCB=180°﹣90°﹣48°=42°.
22.如图,过点A(0,2),B(3,0)的直线AB与直线CD:y=x﹣4交于D,C为直线CD与y轴的交点,求:
(1)直线AB对应的函数表达式;
(2)求S△ADC.
【分析】(1)根据待定系数法即可求得;
(2)由y=x﹣4求得C的坐标,解析式联立,解方程组求得D的坐标,然后根据三角形面积公式即可求得.
解:(1)设直线AB的解析式为y=kx+b,
把A(0,2),B(3,0)分别代入,
得,解得,
所以直线AB的解析式为y=﹣x+2;
(2)过点D作DM⊥y轴,垂足为M,
∵y=x﹣4,
∴当x=0时,y=﹣4,则C(0,﹣4),
解方程组,得,
则D(6,﹣2),
∴DM=6,
∵C(0,﹣4),A(0,2),
∴AC=6,
所以S△ADC=AC?DM=×6×6=18.
23.金都百货电器商场销售进价分别为120元、190元的A、B两种型号的电风扇,第一批货两周销售完毕,如表所示是近二周的销售情况(进价、售价均保持不变,利润=销售收入﹣进货成本):
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 5 7 2570
第二周 8 9 3540
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场再购进这两种型号的电风扇共120台,并且全部销售完,该商场能否实现这两批电风扇的总利润为8310元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【分析】(1)设A种型号的电风扇的销售单价为x元/台,B种型号的电风扇的销售单价为y元/台,由题意列出方程组,可求解;
(2)设再购进A种型号的电风扇m台,则购进B种型号的电风扇(120﹣m)台,由总利润为8310元,列出方程可求解.
解:(1)设A种型号的电风扇的销售单价为x元/台,B种型号的电风扇的销售单价为y元/台,
依题意得:,
解得:,
答:A种型号的电风扇的销售单价为150元/台,B种型号的电风扇的销售单价为260元/台.
(2)设再购进A种型号的电风扇m台,则购进B种型号的电风扇(120﹣m)台,
依题意,得:(150﹣120)(5+8+m)+(260﹣190)(120﹣m+7+9)=8310,
解得:m=40,
∴120﹣m=80.
答:再购进A种型号的电风扇40台,B种型号的电风扇80台,就能实现这两批电风扇的总利润为8310元的目标.
24.三角形ABC中,D是AB上一点,DE∥BC交AC于点E,点F是线段DE延长线上一点,连接FC,∠BCF+∠ADE=180°.
(1)如图2,连接BE,若∠ABE=40°,∠ACF=60°,求∠BEC的度数;
(2)如图3,在(1)的条件下,点G是线段FC延长线上一点,若∠EBC:∠ECB=3:5,BE平分∠ABG,求∠CBG的度数.
【分析】(1)如图2,过点E作EK∥AB,可得CF∥AB∥EK,再根据平行线的性质即可得结论;
(2)根据∠EBC:∠ECB=3:5,可以设∠EBC=3x°,则∠ECB=5x°,然后根据∠AED+∠DEB+∠BEC=180°,3x+5x+100=180,求出x的值,进而可得结果.
解:(1)过点E作EK∥AB,
∵DE∥BC,
∴∠ADE=∠ABC,
∵∠BCF+∠ADE=180°,
∴∠BCF+∠ABC=180°,
∴CF∥AB,
∵EK∥AB,
∴CF∥EK,∠BEK=∠ABE=40°,
∴∠CEK=∠ACF=60°,
∴∠BEC=∠BEK+∠CEK=40°+60°=100°;
(2)∵BE平分∠ABG,
∴∠EBG=∠ABE=40°,
∵∠EBC:∠ECB=3:5,
∴设∠EBC=3x°,则∠ECB=5x°,
∵DE∥BC,
∴∠DEB=∠EBC=3x°,∠AED=∠ECB=5x°,
∵∠AED+∠DEB+∠BEC=180°,
∴3x+5x+100=180,
解得x=10,
∴∠EBC=3x°=30°,
∴∠CBG=∠EBG﹣∠EBC=40°﹣30°=10°.
25.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地时,求货车与甲地的距离;
(2)求线段CD对应的函数表达式;
(3)在轿车行进过程,轿车行驶多少时间,两车相距15千米.
【分析】(1)根据函数图象中的数据,可以得到货车的速度和轿车到达乙地的时间,然后即可计算出轿车到达乙地时,货车与甲地的距离;
(2)根据函数图象中的数据,可以得到线段CD对应的函数表达式;
(3)根据题意和函数图象中的数据,可以计算出在轿车行进过程,轿车行驶多少时间,两车相距15千米.
解:(1)由图象可得,
货车的速度为300÷5=60(千米/小时),
则轿车到达乙地时,货车与甲地的距离是60×4.5=270(千米),
即轿车到达乙地时,货车与甲地的距离是270千米;
(2)设线段CD对应的函数表达式是y=kx+b,
∵点C(2.5,80),点D(4.5,300),
∴,
解得,
即线段CD对应的函数表达式是y=110x﹣195(2.5≤x≤4.5);
(3)当x=2.5时,两车之间的距离为:60×2.5﹣80=70,
∵70>15,
∴在轿车行进过程,两车相距15千米时间是在2.5~4.5之间,
由图象可得,线段OA对应的函数解析式为y=60x,
则|60x﹣(110x﹣195)|=15,
解得x1=3.6,x2=4.2,
∵轿车比货车晚出发1.5小时,3.6﹣1.5=2.1(小时),4.2﹣1.5=2.7(小时),
∴在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米,
答:在轿车行进过程,轿车行驶2.1小时或2.7小时,两车相距15千米.
同课章节目录
