2020-2021学年湖南省永州市道县九年级(下)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年湖南省永州市道县九年级(下)期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 910.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-05 05:19:11 | ||
图片预览



文档简介
2020-2021学年湖南省永州市道县九年级(下)期中数学试卷
一、选择题(本大题共10个小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将你认为正确的选项用2B铅笔涂在答题卡上)
1.﹣(﹣6)的相反数是( )
A. B. C.﹣6 D.6
2.如图,AD∥BC,∠ABD=∠D,∠A=110°,则∠DBC的度数是( )
A.70° B.35° C.40° D.30°
3.图为正方体的展开图,那么在原正方体中与“5”字所在面相对的面上的字为( )
A.1 B.4 C.6 D.3
4.据科学家统计,目前地球上已经被定义、命名的生物约有1500万种左右,数字1500万用科学记数法表示为( )
A.1.5×103 B.1.5×106 C.1.5×107 D.15×106
5.在△ABC中,已知AB=AC,且∠A=70°,则∠B=( )
A.55° B.50° C.70° D.75°
6.小勇投标训练4次的成绩分别是(单位:环)9,9,x,8.已知这组数据的众数和平均数相等,则这组数据中x是( )
A.8 B.9 C.10 D.7
7.下列计算正确的是( )
A.﹣(2x2)3=8x6 B.x5÷x2=x3
C.3x2×2x3=6x6 D.
8.函数中自变量x的取值范围是( )
A.x≥﹣4 B.x≥2 C.x≠﹣4 D.x≠﹣4且x≠2
9.已知:点A(﹣1,y1),B(1,y2),C(2,y3)都在反比例函数图象上(k<0),则y1、y2、y3的关系是( )
A.y3<y1<y2 B.y1<y2<y3 C.y2<y3<y1 D.y3<y2<y1
10.如图,在菱形ABCD中,∠ABC=120°,对角线AC=8,则菱形ABCD的周长为( )
A.32 B.24 C.8 D.16
二、填空题(本大题共8个小题,每小题4分,共32分,请将答案填在答题卡的答案栏内)
11.若x+=5,则= .
12.小军同学在解一元二次方程x2﹣5x+c=0时,正确解得x1=﹣1,x2=6,则c的值为 .
13.圆锥底面圆的半径为5cm,母线长为8cm,则它的侧面积为 cm2(用含π的式子表示).
14.质检部门从2000件电子元件中随机抽取100件进行检测,其中有3件是次品.试据此估计这批电子元件中大约有 件次品.
15.因式分解:4x2﹣64= .
16.把二次函数y=x2+bx+c的图象向下平移2个单位长度,再向左平移1个单位长度后,得到的抛物线的顶点坐标为(﹣2,1),则b﹣c的值为 .
17.如图,在平行四边形ABCO中,∠C=60°,点A,B在⊙O上,点D在优弧上,DA=DB,则∠AOD的度数为 .
18.如图,在平面直角坐标系xOy中,已知A(﹣3,0)和B(0,1),形状相同的抛物线?n(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,根据上述规律,抛物线C1的顶点坐标为 ;抛物线C6的顶点坐标为 .
三、解答题(本题共8个小题,共78分,请将答案填在答题卡上对应的题号处)
19.计算:.
20.先化简,再求值:,其中.
21.如图,在△ABC中,AB=BC,BD平分∠ABC,交AC于点D,四边形ABED是平行四边形,DE交BC于点F,连接CE,求证:BC=DE.
22.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
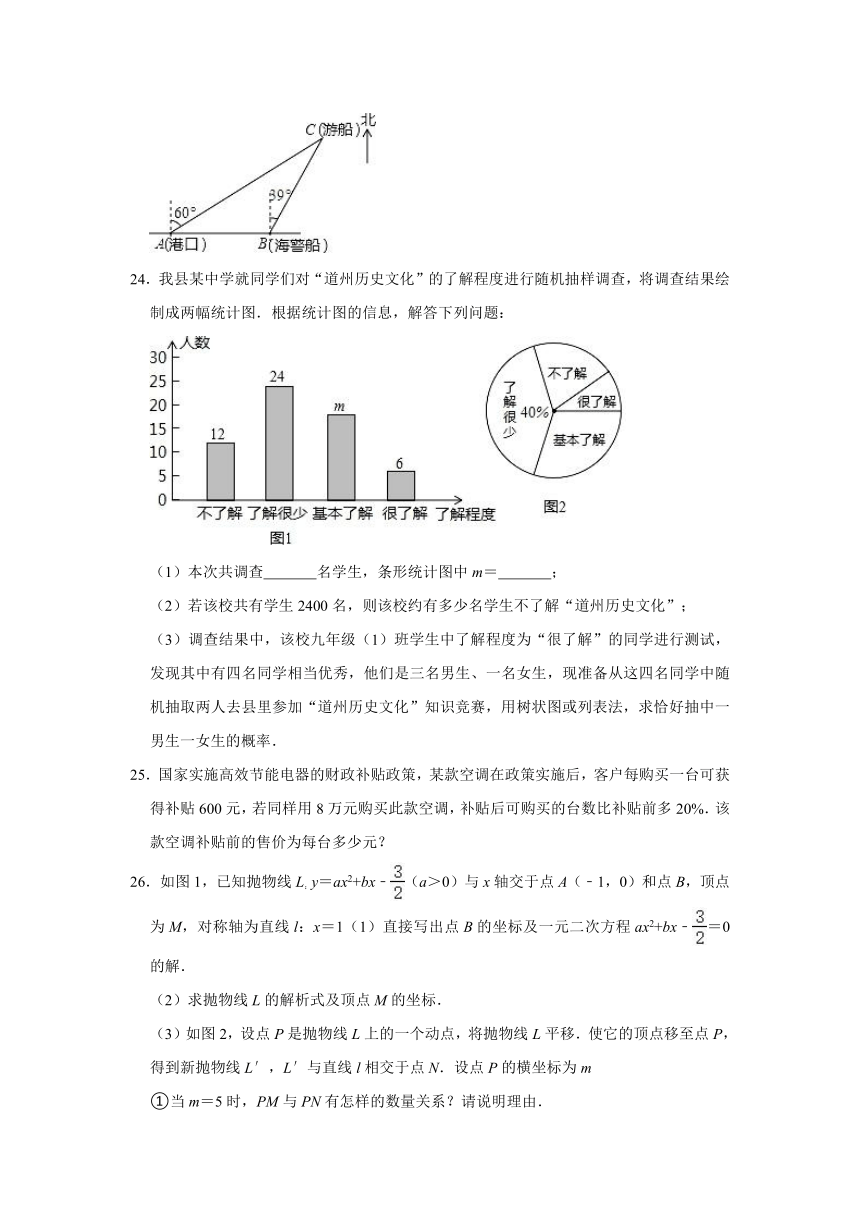
23.如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时)
24.我县某中学就同学们对“道州历史文化”的了解程度进行随机抽样调查,将调查结果绘制成两幅统计图.根据统计图的信息,解答下列问题:
(1)本次共调查 名学生,条形统计图中m= ;
(2)若该校共有学生2400名,则该校约有多少名学生不了解“道州历史文化”;
(3)调查结果中,该校九年级(1)班学生中了解程度为“很了解”的同学进行测试,发现其中有四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人去县里参加“道州历史文化”知识竞赛,用树状图或列表法,求恰好抽中一男生一女生的概率.
25.国家实施高效节能电器的财政补贴政策,某款空调在政策实施后,客户每购买一台可获得补贴600元,若同样用8万元购买此款空调,补贴后可购买的台数比补贴前多20%.该款空调补贴前的售价为每台多少元?
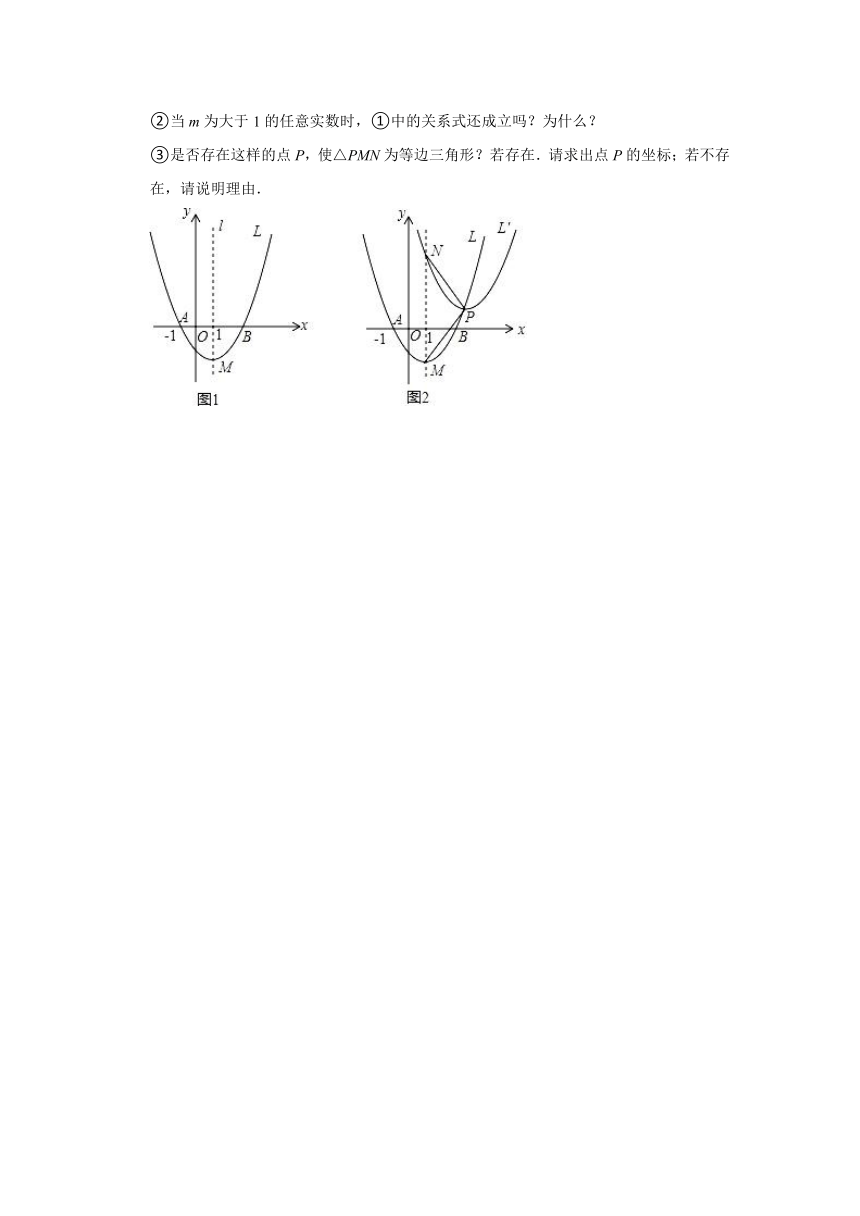
26.如图1,已知抛物线L:y=ax2+bx﹣(a>0)与x轴交于点A(﹣1,0)和点B,顶点为M,对称轴为直线l:x=1(1)直接写出点B的坐标及一元二次方程ax2+bx﹣=0的解.
(2)求抛物线L的解析式及顶点M的坐标.
(3)如图2,设点P是抛物线L上的一个动点,将抛物线L平移.使它的顶点移至点P,得到新抛物线L′,L′与直线l相交于点N.设点P的横坐标为m
①当m=5时,PM与PN有怎样的数量关系?请说明理由.
②当m为大于1的任意实数时,①中的关系式还成立吗?为什么?
③是否存在这样的点P,使△PMN为等边三角形?若存在.请求出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题(本大题共10个小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将你认为正确的选项用2B铅笔涂在答题卡上)
1.﹣(﹣6)的相反数是( )
A. B. C.﹣6 D.6
解:﹣(﹣6)=6,
故﹣(﹣6)的相反数是﹣6.
故选:C.
2.如图,AD∥BC,∠ABD=∠D,∠A=110°,则∠DBC的度数是( )
A.70° B.35° C.40° D.30°
解:∵∠ABD=∠D,∠A=110°,∠ABD+∠D+∠A=180°,
∴∠ABD=∠D=35°.
又∵AD∥BC,
∴∠DBC=∠D=35°.
故选:B.
3.图为正方体的展开图,那么在原正方体中与“5”字所在面相对的面上的字为( )
A.1 B.4 C.6 D.3
解:由正方体表面展开图的“相间、Z端是对面”可知,
“1”与“5”是对面,
“2”与“4”是对面,
“3”与“6”是对面,
故选:A.
4.据科学家统计,目前地球上已经被定义、命名的生物约有1500万种左右,数字1500万用科学记数法表示为( )
A.1.5×103 B.1.5×106 C.1.5×107 D.15×106
解:1500万=15000000=1.5×107.
故选:C.
5.在△ABC中,已知AB=AC,且∠A=70°,则∠B=( )
A.55° B.50° C.70° D.75°
解:∵AB=AC,
∴∠B=∠C,
∵∠A=70°,
∴∠B=(180°﹣70°)÷2=55°.
故选:A.
6.小勇投标训练4次的成绩分别是(单位:环)9,9,x,8.已知这组数据的众数和平均数相等,则这组数据中x是( )
A.8 B.9 C.10 D.7
解:∵四次成绩分别是9,9,x,8,
①当x=8时,众数=9或8,
平均数=8.5,
∵8.5≠9或8,
∴此种情况不合题意,舍去;
②当x≠8时,那么众数=9,
∴=9,
解得x=10.
故选:C.
7.下列计算正确的是( )
A.﹣(2x2)3=8x6 B.x5÷x2=x3
C.3x2×2x3=6x6 D.
解:A、﹣(2x2)3=﹣8x6,故此选项错误;
B、x5÷x2=x3,故此选项正确;
C、3x2×2x3=6x5,故此选项错误;
D、×40=,故此选项错误.
故选:B.
8.函数中自变量x的取值范围是( )
A.x≥﹣4 B.x≥2 C.x≠﹣4 D.x≠﹣4且x≠2
解:由题意得,x﹣2≥0,x+4≠0,
解得,x≥2,
故选:B.
9.已知:点A(﹣1,y1),B(1,y2),C(2,y3)都在反比例函数图象上(k<0),则y1、y2、y3的关系是( )
A.y3<y1<y2 B.y1<y2<y3 C.y2<y3<y1 D.y3<y2<y1
解:在反比例函数中,∵k<0,
∴反比例函数图象在第二、四象限,在每一象限内y随x的增大而增大.
∵A(﹣1,y1),B(1,y2),C(2,y3),
∴A(﹣1,y1)在第二象限,B(1,y2),C(2,y3)在第四象限.
∴y1>0,y2<0,y3<0.
又∵1<2,
∴y2<y3<0.
∴y2<y3<y1.
故选:C.
10.如图,在菱形ABCD中,∠ABC=120°,对角线AC=8,则菱形ABCD的周长为( )
A.32 B.24 C.8 D.16
解:连接BD,AC交于点O,如图:
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=OC=AC=4,∠ABD=∠CBD=∠ABC=60°,
∴∠BAO=30°,
∴OB=OA=4,AB=2OB=8,
∴菱形ABCD的周长=4AB=32;
故选:A.
二、填空题(本大题共8个小题,每小题4分,共32分,请将答案填在答题卡的答案栏内)
11.若x+=5,则= .
解:将x+=5,两边平方得:(x+)2=x2++2=25,即x2+=23,
则原式==.
故答案为:
12.小军同学在解一元二次方程x2﹣5x+c=0时,正确解得x1=﹣1,x2=6,则c的值为 ﹣6 .
解:解方程x2﹣5x+c=0得x1=﹣1,x2=6,
∴x1x2=c=﹣1×6,
∴c=﹣6,
故答案为:﹣6.
13.圆锥底面圆的半径为5cm,母线长为8cm,则它的侧面积为 40π cm2(用含π的式子表示).
解:底面半径为5cm,则底面周长=10πcm,侧面面积=×10π×8=40πcm2.
14.质检部门从2000件电子元件中随机抽取100件进行检测,其中有3件是次品.试据此估计这批电子元件中大约有 60 件次品.
解:估计这批电子元件中次品大约有2000×=60(件),
故答案为:60.
15.因式分解:4x2﹣64= 4(x+4)(x﹣4) .
解:4x2﹣64
=4(x2﹣16)
=4(x+4)(x﹣4).
故答案为:4(x+4)(x﹣4).
16.把二次函数y=x2+bx+c的图象向下平移2个单位长度,再向左平移1个单位长度后,得到的抛物线的顶点坐标为(﹣2,1),则b﹣c的值为 ﹣2 .
解:根据题意y=x2+bx+c=(x+)2+c﹣下平移2个单位,再向左平移1个单位,得y=(x++1)2+c﹣﹣2.
∵抛物线的顶点坐标为(﹣2,1),
∴﹣﹣1=﹣2,c﹣﹣2=1,
解得:b=2,c=4,
∴b﹣c=﹣2,
故答案为:﹣2.
17.如图,在平行四边形ABCO中,∠C=60°,点A,B在⊙O上,点D在优弧上,DA=DB,则∠AOD的度数为 150° .
解:连接OB,如图所示:
∵四边形ABCO是平行四边形,
∴∠OAB=∠C=60°,
∵OA=OB,
∴∠OBA=∠OAB=60°,
∴∠AOB=180°﹣60°﹣60°=60°,
∵DA=DB,
∴=,
∴∠AOD=∠BOD=(360°﹣60°)=150°,
故答案为:150°.
18.如图,在平面直角坐标系xOy中,已知A(﹣3,0)和B(0,1),形状相同的抛物线?n(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,根据上述规律,抛物线C1的顶点坐标为 (2,) ;抛物线C6的顶点坐标为 (21,8) .
解:设直线AB的解析式为y=kx+b,(k≠0),
∵A(﹣3,0),B(0,1),
∴,
解得,
∴直线AB的解析式为y=x+1,
∵对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,
∴y1=+1=,
∴抛物线C1的顶点坐标为 (2,),
观察发现:每个数都是前两个数的和,
∴抛物线C6的顶点坐标的横坐标为21,
∴抛物线C6的顶点坐标为(21,8),
故答案为(2,),(21,8).
三、解答题(本题共8个小题,共78分,请将答案填在答题卡上对应的题号处)
19.计算:.
解:
=﹣1+6×﹣2+1
=﹣1+3﹣2+1
=.
20.先化简,再求值:,其中.
解:
=,
=
=,
=.
=,
当 时,原式=.
21.如图,在△ABC中,AB=BC,BD平分∠ABC,交AC于点D,四边形ABED是平行四边形,DE交BC于点F,连接CE,求证:BC=DE.
【解答】证明:∵AB=BC,BD平分∠ABC,
∴BD⊥AC,AD=CD,
∵四边形ABED是平行四边形,
∴BE∥AD,BE=AD,
∴BE∥CD,BE=CD,
∴四边形BECD是平行四边形,
∵BD⊥AC,
∴∠BDC=90°,
∴平行四边形BECD是矩形,
∴BC=DE.
22.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
解:(1)如图,连接OE,
∵ED⊥EB,
∴∠DEB=90°,
∴BD是⊙O的直径,
∵OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠CBE,
∴∠OEB=∠CBE,
∴OE∥BC,
又∵∠C=90°,
∴∠AEO=90°,即OE⊥AC,
∴AC为⊙O的切线;
(2)∵ED⊥BE,
∴∠BED=∠C=90°,
又∵∠DBE=∠EBC,
∴△BDE∽△BEC,
∴=,即=,
∴BC=;
∵∠AEO=∠C=90°,∠A=∠A,
∴△AOE∽△ABC,
∴=,即=,
解得:AD=.
23.如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时)
解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,
∴CD=AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠BCD=39°,
∴BC==海里,
∴海警船到大事故船C处所需的时间大约为:÷40=≈1.29(小时).
答:海警船到大事故船C处所需的大约时间为1.29小时.
24.我县某中学就同学们对“道州历史文化”的了解程度进行随机抽样调查,将调查结果绘制成两幅统计图.根据统计图的信息,解答下列问题:
(1)本次共调查 60 名学生,条形统计图中m= 18 ;
(2)若该校共有学生2400名,则该校约有多少名学生不了解“道州历史文化”;
(3)调查结果中,该校九年级(1)班学生中了解程度为“很了解”的同学进行测试,发现其中有四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人去县里参加“道州历史文化”知识竞赛,用树状图或列表法,求恰好抽中一男生一女生的概率.
解:(1)由题目图表提供的信息可知总人数为24÷40%=60(名),
m=60﹣12﹣24﹣6=18,
故答案为:60,18;
(2)2400×=480(名),
所以该校约有480名学生不了解“道州历史文化”;
(3)列表如下:
男 男 男 女
男
(男,男) (男,男) (男,女)
男 (男,男)
(男,男) (男,女)
男 (男,男) (男,男)
(男,女)
女 (女,男) (女,男) (女,男)
由上表可知,共12种可能,其中一男一女的可能性有6种,
∴恰好抽中一男生一女生的概率为=.
25.国家实施高效节能电器的财政补贴政策,某款空调在政策实施后,客户每购买一台可获得补贴600元,若同样用8万元购买此款空调,补贴后可购买的台数比补贴前多20%.该款空调补贴前的售价为每台多少元?
解:设该款空调补贴前的售价为每台x元,
由题意,得:×(1+20%)=,
解得:x=3600,
经检验得:x=3600是原方程的根,
答:该款空调补贴前的售价为每台3600元.
26.如图1,已知抛物线L:y=ax2+bx﹣(a>0)与x轴交于点A(﹣1,0)和点B,顶点为M,对称轴为直线l:x=1(1)直接写出点B的坐标及一元二次方程ax2+bx﹣=0的解.
(2)求抛物线L的解析式及顶点M的坐标.
(3)如图2,设点P是抛物线L上的一个动点,将抛物线L平移.使它的顶点移至点P,得到新抛物线L′,L′与直线l相交于点N.设点P的横坐标为m
①当m=5时,PM与PN有怎样的数量关系?请说明理由.
②当m为大于1的任意实数时,①中的关系式还成立吗?为什么?
③是否存在这样的点P,使△PMN为等边三角形?若存在.请求出点P的坐标;若不存在,请说明理由.
解:(1)如图1,∵y=ax2+bx﹣(a>0)与x轴交于点A(﹣1,0)和点B,对称轴为直线l:x=1,
∴点A和点B关于直线l:x=1对称,
∴点B(3,0),
∴一元二次方程ax2+bx﹣=0的解为x1=﹣1,x2=3;
(2)把A(﹣1,0),B(3,0)代入y=ax2+bx﹣,
得,
解得,
抛物线L的解析式为y=x2﹣x﹣,
配方得,y=(x﹣1)2﹣2,
所以顶点M的坐标为(1,﹣2);
(3)如图2,作PC⊥l于点C.
①∵y=(x﹣1)2﹣2,
∴当m=5,即x=5时,y=6,
∴P(5,6),
∴此时L′的解析式为y=(x﹣5)2+6,点C的坐标是(1,6).
∵当x=1时,y=14,
∴点N的坐标是(1,14).
∵CM=6﹣(﹣2)=8,CN=14﹣6=8,
∴CM=CN.
∵PC垂直平分线段MN,
∴PM=PN;
②PM=PN仍然成立.
由题意有点P的坐标为(m,m2﹣m﹣).
∵L′的解析式为y=(x﹣m)2+m2﹣m﹣,
∴点C的坐标是(1,m2﹣m﹣),
∴CM=m2﹣m﹣+2=m2﹣m+.
∵在L′的解析式y=(x﹣m)2+m2﹣m﹣中,
∴当x=1时,y=m2﹣2m﹣1,
∴点N的坐标是(1,m2﹣2m﹣1),
∴CN=(m2﹣2m﹣1)﹣(m2﹣m﹣)=m2﹣m+,
∴CM=CN.
∵PC垂直平分线段MN,
∴PM=PN;
③存在这样的点P,使△PMN为等边三角形.
若=tan30°,则m2﹣m+=(m﹣1),
解得m=,
所以点P的坐标为(,﹣).
一、选择题(本大题共10个小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将你认为正确的选项用2B铅笔涂在答题卡上)
1.﹣(﹣6)的相反数是( )
A. B. C.﹣6 D.6
2.如图,AD∥BC,∠ABD=∠D,∠A=110°,则∠DBC的度数是( )
A.70° B.35° C.40° D.30°
3.图为正方体的展开图,那么在原正方体中与“5”字所在面相对的面上的字为( )
A.1 B.4 C.6 D.3
4.据科学家统计,目前地球上已经被定义、命名的生物约有1500万种左右,数字1500万用科学记数法表示为( )
A.1.5×103 B.1.5×106 C.1.5×107 D.15×106
5.在△ABC中,已知AB=AC,且∠A=70°,则∠B=( )
A.55° B.50° C.70° D.75°
6.小勇投标训练4次的成绩分别是(单位:环)9,9,x,8.已知这组数据的众数和平均数相等,则这组数据中x是( )
A.8 B.9 C.10 D.7
7.下列计算正确的是( )
A.﹣(2x2)3=8x6 B.x5÷x2=x3
C.3x2×2x3=6x6 D.
8.函数中自变量x的取值范围是( )
A.x≥﹣4 B.x≥2 C.x≠﹣4 D.x≠﹣4且x≠2
9.已知:点A(﹣1,y1),B(1,y2),C(2,y3)都在反比例函数图象上(k<0),则y1、y2、y3的关系是( )
A.y3<y1<y2 B.y1<y2<y3 C.y2<y3<y1 D.y3<y2<y1
10.如图,在菱形ABCD中,∠ABC=120°,对角线AC=8,则菱形ABCD的周长为( )
A.32 B.24 C.8 D.16
二、填空题(本大题共8个小题,每小题4分,共32分,请将答案填在答题卡的答案栏内)
11.若x+=5,则= .
12.小军同学在解一元二次方程x2﹣5x+c=0时,正确解得x1=﹣1,x2=6,则c的值为 .
13.圆锥底面圆的半径为5cm,母线长为8cm,则它的侧面积为 cm2(用含π的式子表示).
14.质检部门从2000件电子元件中随机抽取100件进行检测,其中有3件是次品.试据此估计这批电子元件中大约有 件次品.
15.因式分解:4x2﹣64= .
16.把二次函数y=x2+bx+c的图象向下平移2个单位长度,再向左平移1个单位长度后,得到的抛物线的顶点坐标为(﹣2,1),则b﹣c的值为 .
17.如图,在平行四边形ABCO中,∠C=60°,点A,B在⊙O上,点D在优弧上,DA=DB,则∠AOD的度数为 .
18.如图,在平面直角坐标系xOy中,已知A(﹣3,0)和B(0,1),形状相同的抛物线?n(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,根据上述规律,抛物线C1的顶点坐标为 ;抛物线C6的顶点坐标为 .
三、解答题(本题共8个小题,共78分,请将答案填在答题卡上对应的题号处)
19.计算:.
20.先化简,再求值:,其中.
21.如图,在△ABC中,AB=BC,BD平分∠ABC,交AC于点D,四边形ABED是平行四边形,DE交BC于点F,连接CE,求证:BC=DE.
22.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
23.如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时)
24.我县某中学就同学们对“道州历史文化”的了解程度进行随机抽样调查,将调查结果绘制成两幅统计图.根据统计图的信息,解答下列问题:
(1)本次共调查 名学生,条形统计图中m= ;
(2)若该校共有学生2400名,则该校约有多少名学生不了解“道州历史文化”;
(3)调查结果中,该校九年级(1)班学生中了解程度为“很了解”的同学进行测试,发现其中有四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人去县里参加“道州历史文化”知识竞赛,用树状图或列表法,求恰好抽中一男生一女生的概率.
25.国家实施高效节能电器的财政补贴政策,某款空调在政策实施后,客户每购买一台可获得补贴600元,若同样用8万元购买此款空调,补贴后可购买的台数比补贴前多20%.该款空调补贴前的售价为每台多少元?
26.如图1,已知抛物线L:y=ax2+bx﹣(a>0)与x轴交于点A(﹣1,0)和点B,顶点为M,对称轴为直线l:x=1(1)直接写出点B的坐标及一元二次方程ax2+bx﹣=0的解.
(2)求抛物线L的解析式及顶点M的坐标.
(3)如图2,设点P是抛物线L上的一个动点,将抛物线L平移.使它的顶点移至点P,得到新抛物线L′,L′与直线l相交于点N.设点P的横坐标为m
①当m=5时,PM与PN有怎样的数量关系?请说明理由.
②当m为大于1的任意实数时,①中的关系式还成立吗?为什么?
③是否存在这样的点P,使△PMN为等边三角形?若存在.请求出点P的坐标;若不存在,请说明理由.
参考答案
一、选择题(本大题共10个小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将你认为正确的选项用2B铅笔涂在答题卡上)
1.﹣(﹣6)的相反数是( )
A. B. C.﹣6 D.6
解:﹣(﹣6)=6,
故﹣(﹣6)的相反数是﹣6.
故选:C.
2.如图,AD∥BC,∠ABD=∠D,∠A=110°,则∠DBC的度数是( )
A.70° B.35° C.40° D.30°
解:∵∠ABD=∠D,∠A=110°,∠ABD+∠D+∠A=180°,
∴∠ABD=∠D=35°.
又∵AD∥BC,
∴∠DBC=∠D=35°.
故选:B.
3.图为正方体的展开图,那么在原正方体中与“5”字所在面相对的面上的字为( )
A.1 B.4 C.6 D.3
解:由正方体表面展开图的“相间、Z端是对面”可知,
“1”与“5”是对面,
“2”与“4”是对面,
“3”与“6”是对面,
故选:A.
4.据科学家统计,目前地球上已经被定义、命名的生物约有1500万种左右,数字1500万用科学记数法表示为( )
A.1.5×103 B.1.5×106 C.1.5×107 D.15×106
解:1500万=15000000=1.5×107.
故选:C.
5.在△ABC中,已知AB=AC,且∠A=70°,则∠B=( )
A.55° B.50° C.70° D.75°
解:∵AB=AC,
∴∠B=∠C,
∵∠A=70°,
∴∠B=(180°﹣70°)÷2=55°.
故选:A.
6.小勇投标训练4次的成绩分别是(单位:环)9,9,x,8.已知这组数据的众数和平均数相等,则这组数据中x是( )
A.8 B.9 C.10 D.7
解:∵四次成绩分别是9,9,x,8,
①当x=8时,众数=9或8,
平均数=8.5,
∵8.5≠9或8,
∴此种情况不合题意,舍去;
②当x≠8时,那么众数=9,
∴=9,
解得x=10.
故选:C.
7.下列计算正确的是( )
A.﹣(2x2)3=8x6 B.x5÷x2=x3
C.3x2×2x3=6x6 D.
解:A、﹣(2x2)3=﹣8x6,故此选项错误;
B、x5÷x2=x3,故此选项正确;
C、3x2×2x3=6x5,故此选项错误;
D、×40=,故此选项错误.
故选:B.
8.函数中自变量x的取值范围是( )
A.x≥﹣4 B.x≥2 C.x≠﹣4 D.x≠﹣4且x≠2
解:由题意得,x﹣2≥0,x+4≠0,
解得,x≥2,
故选:B.
9.已知:点A(﹣1,y1),B(1,y2),C(2,y3)都在反比例函数图象上(k<0),则y1、y2、y3的关系是( )
A.y3<y1<y2 B.y1<y2<y3 C.y2<y3<y1 D.y3<y2<y1
解:在反比例函数中,∵k<0,
∴反比例函数图象在第二、四象限,在每一象限内y随x的增大而增大.
∵A(﹣1,y1),B(1,y2),C(2,y3),
∴A(﹣1,y1)在第二象限,B(1,y2),C(2,y3)在第四象限.
∴y1>0,y2<0,y3<0.
又∵1<2,
∴y2<y3<0.
∴y2<y3<y1.
故选:C.
10.如图,在菱形ABCD中,∠ABC=120°,对角线AC=8,则菱形ABCD的周长为( )
A.32 B.24 C.8 D.16
解:连接BD,AC交于点O,如图:
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=OC=AC=4,∠ABD=∠CBD=∠ABC=60°,
∴∠BAO=30°,
∴OB=OA=4,AB=2OB=8,
∴菱形ABCD的周长=4AB=32;
故选:A.
二、填空题(本大题共8个小题,每小题4分,共32分,请将答案填在答题卡的答案栏内)
11.若x+=5,则= .
解:将x+=5,两边平方得:(x+)2=x2++2=25,即x2+=23,
则原式==.
故答案为:
12.小军同学在解一元二次方程x2﹣5x+c=0时,正确解得x1=﹣1,x2=6,则c的值为 ﹣6 .
解:解方程x2﹣5x+c=0得x1=﹣1,x2=6,
∴x1x2=c=﹣1×6,
∴c=﹣6,
故答案为:﹣6.
13.圆锥底面圆的半径为5cm,母线长为8cm,则它的侧面积为 40π cm2(用含π的式子表示).
解:底面半径为5cm,则底面周长=10πcm,侧面面积=×10π×8=40πcm2.
14.质检部门从2000件电子元件中随机抽取100件进行检测,其中有3件是次品.试据此估计这批电子元件中大约有 60 件次品.
解:估计这批电子元件中次品大约有2000×=60(件),
故答案为:60.
15.因式分解:4x2﹣64= 4(x+4)(x﹣4) .
解:4x2﹣64
=4(x2﹣16)
=4(x+4)(x﹣4).
故答案为:4(x+4)(x﹣4).
16.把二次函数y=x2+bx+c的图象向下平移2个单位长度,再向左平移1个单位长度后,得到的抛物线的顶点坐标为(﹣2,1),则b﹣c的值为 ﹣2 .
解:根据题意y=x2+bx+c=(x+)2+c﹣下平移2个单位,再向左平移1个单位,得y=(x++1)2+c﹣﹣2.
∵抛物线的顶点坐标为(﹣2,1),
∴﹣﹣1=﹣2,c﹣﹣2=1,
解得:b=2,c=4,
∴b﹣c=﹣2,
故答案为:﹣2.
17.如图,在平行四边形ABCO中,∠C=60°,点A,B在⊙O上,点D在优弧上,DA=DB,则∠AOD的度数为 150° .
解:连接OB,如图所示:
∵四边形ABCO是平行四边形,
∴∠OAB=∠C=60°,
∵OA=OB,
∴∠OBA=∠OAB=60°,
∴∠AOB=180°﹣60°﹣60°=60°,
∵DA=DB,
∴=,
∴∠AOD=∠BOD=(360°﹣60°)=150°,
故答案为:150°.
18.如图,在平面直角坐标系xOy中,已知A(﹣3,0)和B(0,1),形状相同的抛物线?n(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,根据上述规律,抛物线C1的顶点坐标为 (2,) ;抛物线C6的顶点坐标为 (21,8) .
解:设直线AB的解析式为y=kx+b,(k≠0),
∵A(﹣3,0),B(0,1),
∴,
解得,
∴直线AB的解析式为y=x+1,
∵对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,
∴y1=+1=,
∴抛物线C1的顶点坐标为 (2,),
观察发现:每个数都是前两个数的和,
∴抛物线C6的顶点坐标的横坐标为21,
∴抛物线C6的顶点坐标为(21,8),
故答案为(2,),(21,8).
三、解答题(本题共8个小题,共78分,请将答案填在答题卡上对应的题号处)
19.计算:.
解:
=﹣1+6×﹣2+1
=﹣1+3﹣2+1
=.
20.先化简,再求值:,其中.
解:
=,
=
=,
=.
=,
当 时,原式=.
21.如图,在△ABC中,AB=BC,BD平分∠ABC,交AC于点D,四边形ABED是平行四边形,DE交BC于点F,连接CE,求证:BC=DE.
【解答】证明:∵AB=BC,BD平分∠ABC,
∴BD⊥AC,AD=CD,
∵四边形ABED是平行四边形,
∴BE∥AD,BE=AD,
∴BE∥CD,BE=CD,
∴四边形BECD是平行四边形,
∵BD⊥AC,
∴∠BDC=90°,
∴平行四边形BECD是矩形,
∴BC=DE.
22.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
解:(1)如图,连接OE,
∵ED⊥EB,
∴∠DEB=90°,
∴BD是⊙O的直径,
∵OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠CBE,
∴∠OEB=∠CBE,
∴OE∥BC,
又∵∠C=90°,
∴∠AEO=90°,即OE⊥AC,
∴AC为⊙O的切线;
(2)∵ED⊥BE,
∴∠BED=∠C=90°,
又∵∠DBE=∠EBC,
∴△BDE∽△BEC,
∴=,即=,
∴BC=;
∵∠AEO=∠C=90°,∠A=∠A,
∴△AOE∽△ABC,
∴=,即=,
解得:AD=.
23.如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时)
解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,
∴CD=AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠BCD=39°,
∴BC==海里,
∴海警船到大事故船C处所需的时间大约为:÷40=≈1.29(小时).
答:海警船到大事故船C处所需的大约时间为1.29小时.
24.我县某中学就同学们对“道州历史文化”的了解程度进行随机抽样调查,将调查结果绘制成两幅统计图.根据统计图的信息,解答下列问题:
(1)本次共调查 60 名学生,条形统计图中m= 18 ;
(2)若该校共有学生2400名,则该校约有多少名学生不了解“道州历史文化”;
(3)调查结果中,该校九年级(1)班学生中了解程度为“很了解”的同学进行测试,发现其中有四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人去县里参加“道州历史文化”知识竞赛,用树状图或列表法,求恰好抽中一男生一女生的概率.
解:(1)由题目图表提供的信息可知总人数为24÷40%=60(名),
m=60﹣12﹣24﹣6=18,
故答案为:60,18;
(2)2400×=480(名),
所以该校约有480名学生不了解“道州历史文化”;
(3)列表如下:
男 男 男 女
男
(男,男) (男,男) (男,女)
男 (男,男)
(男,男) (男,女)
男 (男,男) (男,男)
(男,女)
女 (女,男) (女,男) (女,男)
由上表可知,共12种可能,其中一男一女的可能性有6种,
∴恰好抽中一男生一女生的概率为=.
25.国家实施高效节能电器的财政补贴政策,某款空调在政策实施后,客户每购买一台可获得补贴600元,若同样用8万元购买此款空调,补贴后可购买的台数比补贴前多20%.该款空调补贴前的售价为每台多少元?
解:设该款空调补贴前的售价为每台x元,
由题意,得:×(1+20%)=,
解得:x=3600,
经检验得:x=3600是原方程的根,
答:该款空调补贴前的售价为每台3600元.
26.如图1,已知抛物线L:y=ax2+bx﹣(a>0)与x轴交于点A(﹣1,0)和点B,顶点为M,对称轴为直线l:x=1(1)直接写出点B的坐标及一元二次方程ax2+bx﹣=0的解.
(2)求抛物线L的解析式及顶点M的坐标.
(3)如图2,设点P是抛物线L上的一个动点,将抛物线L平移.使它的顶点移至点P,得到新抛物线L′,L′与直线l相交于点N.设点P的横坐标为m
①当m=5时,PM与PN有怎样的数量关系?请说明理由.
②当m为大于1的任意实数时,①中的关系式还成立吗?为什么?
③是否存在这样的点P,使△PMN为等边三角形?若存在.请求出点P的坐标;若不存在,请说明理由.
解:(1)如图1,∵y=ax2+bx﹣(a>0)与x轴交于点A(﹣1,0)和点B,对称轴为直线l:x=1,
∴点A和点B关于直线l:x=1对称,
∴点B(3,0),
∴一元二次方程ax2+bx﹣=0的解为x1=﹣1,x2=3;
(2)把A(﹣1,0),B(3,0)代入y=ax2+bx﹣,
得,
解得,
抛物线L的解析式为y=x2﹣x﹣,
配方得,y=(x﹣1)2﹣2,
所以顶点M的坐标为(1,﹣2);
(3)如图2,作PC⊥l于点C.
①∵y=(x﹣1)2﹣2,
∴当m=5,即x=5时,y=6,
∴P(5,6),
∴此时L′的解析式为y=(x﹣5)2+6,点C的坐标是(1,6).
∵当x=1时,y=14,
∴点N的坐标是(1,14).
∵CM=6﹣(﹣2)=8,CN=14﹣6=8,
∴CM=CN.
∵PC垂直平分线段MN,
∴PM=PN;
②PM=PN仍然成立.
由题意有点P的坐标为(m,m2﹣m﹣).
∵L′的解析式为y=(x﹣m)2+m2﹣m﹣,
∴点C的坐标是(1,m2﹣m﹣),
∴CM=m2﹣m﹣+2=m2﹣m+.
∵在L′的解析式y=(x﹣m)2+m2﹣m﹣中,
∴当x=1时,y=m2﹣2m﹣1,
∴点N的坐标是(1,m2﹣2m﹣1),
∴CN=(m2﹣2m﹣1)﹣(m2﹣m﹣)=m2﹣m+,
∴CM=CN.
∵PC垂直平分线段MN,
∴PM=PN;
③存在这样的点P,使△PMN为等边三角形.
若=tan30°,则m2﹣m+=(m﹣1),
解得m=,
所以点P的坐标为(,﹣).
同课章节目录
