山东省微山县傅村镇一中2012届九年级3月月考数学试题(无答案)
文档属性
| 名称 | 山东省微山县傅村镇一中2012届九年级3月月考数学试题(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 46.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-04 00:00:00 | ||
图片预览


文档简介
九年级数学下学期第一次月检测试卷
一、选择题(每小题3分,共30分)(请把答案填入表格内)
1.如果是等腰直角三角形的一个锐角,那么的值等于( )
A. B. C. D.
2.如果∠A为锐角,且sinA=0.6,那么( )
A.0°<A<30° B.30°<A<45°
C.45°<A<60° D.60°<A<90°
3.已知△ABC的三边长分别为,,2,△A/B/C/的两边长分别是1和,如果△ABC∽△A/B/C/相似,那么△A/B/C/的第三边长是( )
A. B. C. D.
4.无论m为任何实数,二次函数y=+(2-m)x+m的图象总过的点是( )
A.(1,3) B.(1,0) C.(-1,3) D.(-1,0)
5.下图中几何体的左视图是( )
6、在Rt△ABC中,各边的长度都扩大两倍,那么锐角A的各三角函数值( )
A.都扩大两倍 B.都缩小两倍 C.不变 D.都扩大四倍
7.如图,晚上小亮在路灯下散步,在小亮由处走到处这一过程中,他在地上的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
8.抛物线过第二、三、四象限,则( ) (第7题)
A. B.
C. D.
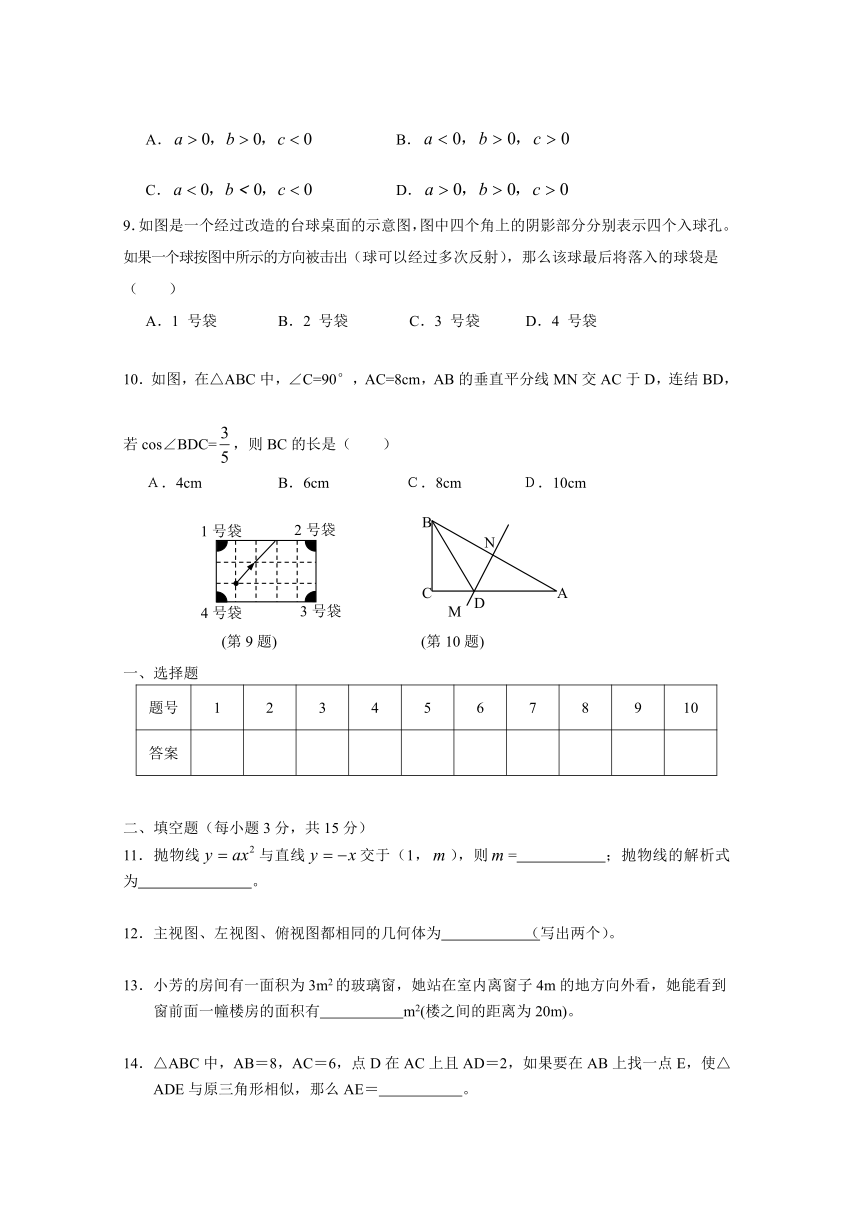
9.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔。如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )
A.1 号袋 B.2 号袋 C.3 号袋 D.4 号袋
10.如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC=,则BC的长是( )
A.4cm B.6cm C.8cm D.10cm
(第9题) (第10题)
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(每小题3分,共15分)
11.抛物线与直线交于(1,),则= ;抛物线的解析式为 。
12.主视图、左视图、俯视图都相同的几何体为 (写出两个)。
13.小芳的房间有一面积为3m2的玻璃窗,她站在室内离窗子4m的地方向外看,她能看到
窗前面一幢楼房的面积有 m2(楼之间的距离为20m)。
14.△ABC中,AB=8,AC=6,点D在AC上且AD=2,如果要在AB上找一点E,使△ADE与原三角形相似,那么AE= 。
15.古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是___________(填序号)
①13 = 3+10 ②25 = 9+16 ③36 = 15+21 ④49 = 18+31
三、解答题(共55分)
16.(5分) 计算:
17.(6分)已知抛物线y=ax2+bx+c(a0)与x轴的两交点的横坐标分别是-1和3,与y轴交点的纵坐标是-;
(1)确定抛物线的解析式;
(2)用配方法确定抛物线的开口方向,对称轴和顶点坐标。
18.(7分)如图,在△ABC中,AB=AC,∠1=∠2。
⑴△ADB和△ABE相似吗?
⑵小明说:“AB2=AD·AE”,你同意吗?
19. (7分)已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m。
(1)请你在图8中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长。
20.(7分)为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如
下的探索:
实践:根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如右示意图的测量方案:把镜子放在离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这是恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算树(AB)的高度。(精确到0.1米)
21.(7分)如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:
(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;
(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
22.(7分)瞭望台AB高20m,从瞭望台底部B测得对面塔顶C的仰角为60°,
从瞭望台顶部A测得塔顶C的仰角为45°,已知瞭望台与塔CD地势
高低相同。求塔高CD。
23.(本题满分9分)丽江古城某客栈客房部有20套房间供游客居住,当每套房间的定价为每天120元时,房间可以住满.当每套房间每天的定价每增加10元时,就会有一套房间空闲.对有游客入住的房间,客栈需对每套房间每天支出20元的各种费用.设每套房间每天的定价增加x元.求:
⑴房间每天的入住量y(套)关于x(元)的函数关系式;
⑵该客栈每天的房间收费总额z(元)关于x(元)的函数关系式;
⑶该客栈客房部每天的利润W(元)关于x(元)的函数关系式;当每套房间的定价为每天多少元时,W有最大值?最大值是多少?
4号袋
2号袋
3号袋
1号袋
A
E
D
C
图8
B
A
B
太
阳
光
线
C
D
E
O
x
y
A
B
C
PAGE
一、选择题(每小题3分,共30分)(请把答案填入表格内)
1.如果是等腰直角三角形的一个锐角,那么的值等于( )
A. B. C. D.
2.如果∠A为锐角,且sinA=0.6,那么( )
A.0°<A<30° B.30°<A<45°
C.45°<A<60° D.60°<A<90°
3.已知△ABC的三边长分别为,,2,△A/B/C/的两边长分别是1和,如果△ABC∽△A/B/C/相似,那么△A/B/C/的第三边长是( )
A. B. C. D.
4.无论m为任何实数,二次函数y=+(2-m)x+m的图象总过的点是( )
A.(1,3) B.(1,0) C.(-1,3) D.(-1,0)
5.下图中几何体的左视图是( )
6、在Rt△ABC中,各边的长度都扩大两倍,那么锐角A的各三角函数值( )
A.都扩大两倍 B.都缩小两倍 C.不变 D.都扩大四倍
7.如图,晚上小亮在路灯下散步,在小亮由处走到处这一过程中,他在地上的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
8.抛物线过第二、三、四象限,则( ) (第7题)
A. B.
C. D.
9.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔。如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是( )
A.1 号袋 B.2 号袋 C.3 号袋 D.4 号袋
10.如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC=,则BC的长是( )
A.4cm B.6cm C.8cm D.10cm
(第9题) (第10题)
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(每小题3分,共15分)
11.抛物线与直线交于(1,),则= ;抛物线的解析式为 。
12.主视图、左视图、俯视图都相同的几何体为 (写出两个)。
13.小芳的房间有一面积为3m2的玻璃窗,她站在室内离窗子4m的地方向外看,她能看到
窗前面一幢楼房的面积有 m2(楼之间的距离为20m)。
14.△ABC中,AB=8,AC=6,点D在AC上且AD=2,如果要在AB上找一点E,使△ADE与原三角形相似,那么AE= 。
15.古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是___________(填序号)
①13 = 3+10 ②25 = 9+16 ③36 = 15+21 ④49 = 18+31
三、解答题(共55分)
16.(5分) 计算:
17.(6分)已知抛物线y=ax2+bx+c(a0)与x轴的两交点的横坐标分别是-1和3,与y轴交点的纵坐标是-;
(1)确定抛物线的解析式;
(2)用配方法确定抛物线的开口方向,对称轴和顶点坐标。
18.(7分)如图,在△ABC中,AB=AC,∠1=∠2。
⑴△ADB和△ABE相似吗?
⑵小明说:“AB2=AD·AE”,你同意吗?
19. (7分)已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m。
(1)请你在图8中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长。
20.(7分)为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如
下的探索:
实践:根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如右示意图的测量方案:把镜子放在离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这是恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算树(AB)的高度。(精确到0.1米)
21.(7分)如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:
(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;
(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
22.(7分)瞭望台AB高20m,从瞭望台底部B测得对面塔顶C的仰角为60°,
从瞭望台顶部A测得塔顶C的仰角为45°,已知瞭望台与塔CD地势
高低相同。求塔高CD。
23.(本题满分9分)丽江古城某客栈客房部有20套房间供游客居住,当每套房间的定价为每天120元时,房间可以住满.当每套房间每天的定价每增加10元时,就会有一套房间空闲.对有游客入住的房间,客栈需对每套房间每天支出20元的各种费用.设每套房间每天的定价增加x元.求:
⑴房间每天的入住量y(套)关于x(元)的函数关系式;
⑵该客栈每天的房间收费总额z(元)关于x(元)的函数关系式;
⑶该客栈客房部每天的利润W(元)关于x(元)的函数关系式;当每套房间的定价为每天多少元时,W有最大值?最大值是多少?
4号袋
2号袋
3号袋
1号袋
A
E
D
C
图8
B
A
B
太
阳
光
线
C
D
E
O
x
y
A
B
C
PAGE
同课章节目录
