四年级下册数学试题一课一练-5.1三角形的特性 人教新版(含答案) (1)
文档属性
| 名称 | 四年级下册数学试题一课一练-5.1三角形的特性 人教新版(含答案) (1) |  | |
| 格式 | docx | ||
| 文件大小 | 48.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-05 21:43:38 | ||
图片预览

文档简介
(
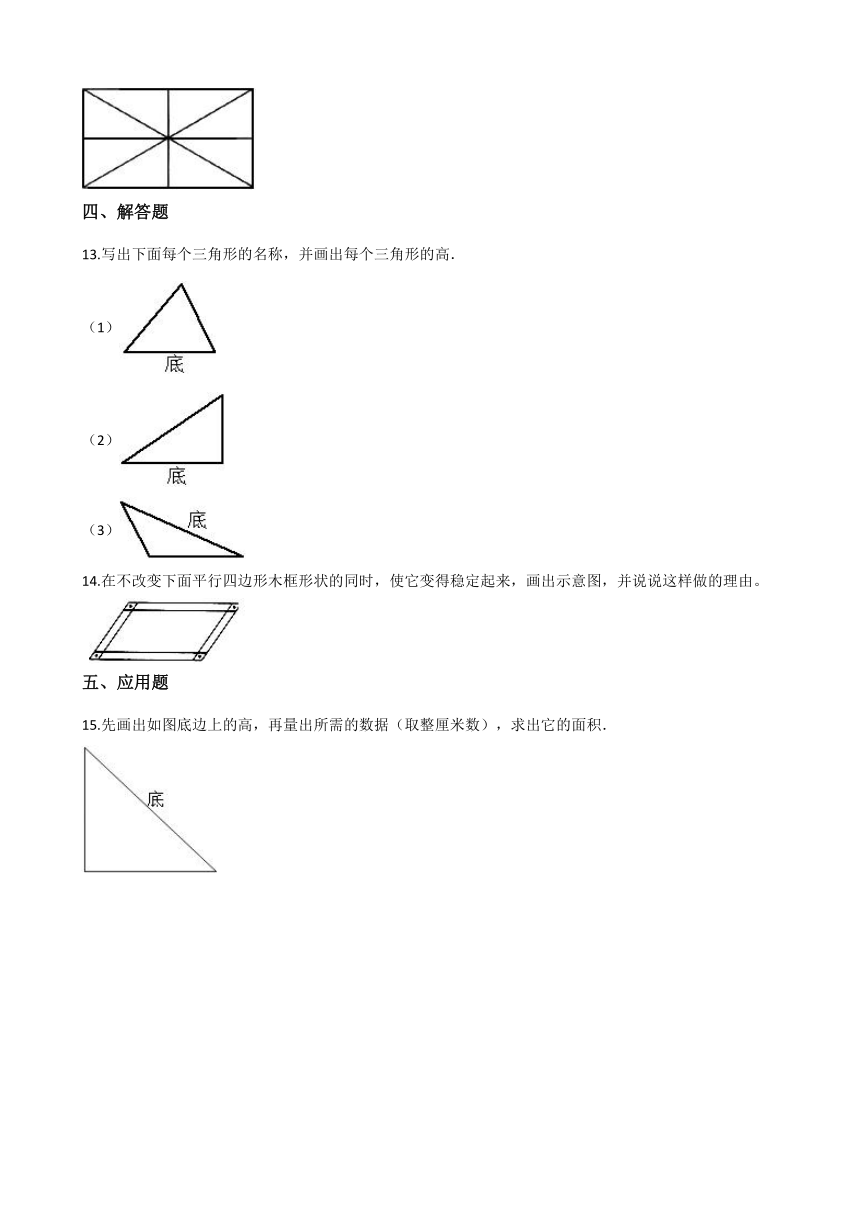
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
四年级下册数学一课一练-5.1三角形的性
一、单选题
1.下图中,点A到直线BC的距离是线段(
??)的长.
A.?AE???????????????????????????????????????????B.?DE???????????????????????????????????????????C.?AD
2.如图,过点A的线段中(?
)线段最短.
A.?AC???????????????????????????????????????????B.?AB???????????????????????????????????????????C.?AD
3.一个三角形的两条边的长度分别是4厘米、5厘米,下列选项中能作为第三条边的长度的是(???
)。
A.?8厘米??????????????????????????????????????B.?9厘米??????????????????????????????????????C.?10厘米
4.下面(???
)组的三条线段能围成一个三角形。
A.?0.5cm、1cm、3cm??????????????????B.?1cm、2.5cm、3cm??????????????????C.?2cm、2cm、4cm
二、判断题
5.用三条线段肯定能围成一个三角形。(???
)
6.连接两点的所有线中,线段最短。(
)
7.任意三条线段都可以围成三角形。
(
)
8.钝角三角形只有一条高.(
??)
三、填空题
9.自行车的车架做成三角形,应用的是三角形具有________性。
10.三角形任意两边之和________第三边,两边之差________第三边。
11.一个三角形,第一条边长是6
cm,第二条边长是7
cm,第三条边长一定小于________cm。
12.图中有________个长方形?________个三角形?________个梯形?
四、解答题
13.写出下面每个三角形的名称,并画出每个三角形的高.
(1)
(2)
(3)
14.在不改变下面平行四边形木框形状的同时,使它变得稳定起来,画出示意图,并说说这样做的理由。
五、应用题
15.先画出如图底边上的高,再量出所需的数据(取整厘米数),求出它的面积.
参考答案
一、单选题
1.【答案】
A
【解析】【解答】点A到直线BC的距离是垂线段AE,
故答案为:A
【分析】直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
2.【答案】
A
【解析】【解答】解:图中过A点到直线BD的所有线段中,最短的一条是AC;
故选:A.
【分析】根据“点到直线的距离,垂线段最短”进行解答即可.解答此题应明确:点到直线的距离,垂线段最短.
3.【答案】
A
【解析】【解答】解:5-4<第三边<5+4
所以1厘米<第三边<9厘米,
所以8厘米符合。
故答案为:A。
【分析】三角形的三边关系:两边之和大于第三边,两边之差小于第三边,本题据此解答即可。
4.【答案】
B
【解析】【解答】选项A,因为0.5+1=1.5,1.5<3,所以0.5cm、1cm、3cm三条线段不能围成一个三角形;
选项B,因为1+2.5=3.5,3.5>3,3-1=2,2<2.5,所以1cm、2.5cm、3cm三条线段能围成一个三角形;
选项C,因为2+2=4,4=4,所以2cm、2cm、4cm三条线段不能围成一个三角形。
故答案为:B。
【分析】在三角形里,任意两边之和大于第三边,任意两边之差小于第三边,据此判断。
二、判断题
5.【答案】
错误
【解析】【解答】用三条线段不一定能围成一个三角形。原题说法错误。
故答案为:错误。
【分析】判断能不能围成三角形的方法:三角形两条短边之和必须大于第三边。
6.【答案】
正确
【解析】【解答】连接两点的所有线中,线段最短,此题说法正确.
故答案为:正确.
【分析】两点之间,线段最短,据此判断.
7.【答案】
错误
【解析】【解答】能围成三角形三边关系:任意两边之和都大于第三边。
【分析】三角形特征:两边之和大于第三边
8.【答案】
错误
【解析】【解答】解:任何三角形都有三个高,
钝角三角形也不例外,只不过它的高,一条在三角形内,两条在三角形外.
故答案为:错误.
【分析】三角形从它的任意顶点到对边都可以做一条高。
三、填空题
9.【答案】
稳定
【解析】【解答】解:自行车的车架做成三角形,应用的是三角形具有稳定性。
?故答案为:稳定。
【分析】三角形具有稳定性。
10.【答案】
大于;小于
【解析】【解答】三角形任意两边之和大于第三边,两边之差小于第三边。
故答案为:大于、小于
【分析】两边之差<三角形第三边的取值范围<两边之和。
11.【答案】
13
【解析】【解答】解:6+7=13(cm)。
故答案为:13。
【分析】三角形任意两边之和小于第三边,所以第三边的长度一定小于已知两条边的长度和。
12.【答案】
9;16;8
【解析】【解答】图中有9个长方形,16个三角形,8个梯形。
【分析】解答此题要根据长方形、三角形、梯形的特点,先数独立的图形,再数由独立的图形组合成的图形。
四、解答题
13.【答案】
(1)解:锐角三角形
(2)解:直角三角形
(3)解:钝角三角形
【解析】【分析】(1)锐角三角形;(2)直角三角形;(3)钝角三角形;画高时过三角形的一个顶点画出对边的垂线段,这条垂线段就是三角形的高.
14.【答案】
解:
【解析】【分析】根据三角形的稳定性可以把平行四边形的对角线连起来即可。
五、应用题
15.【答案】解:如图所示,即为所要求画的三角形已知底边上的高:
;
量得三角形的底约为4厘米,高约为2厘米,
则三角形的面积为:4×2÷2=4(平方厘米);
答:三角形的面积为4平方厘米
【解析】【分析】依据过直线外一点作已知直线的垂线的方法,即可作出已知底上的高;再据量得底和高的值,利用三角形的面积公式即可求其面积.此题主要考查:过直线外一点作已知直线的垂线的方法,以及三角形面积的计算方法.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
四年级下册数学一课一练-5.1三角形的性
一、单选题
1.下图中,点A到直线BC的距离是线段(
??)的长.
A.?AE???????????????????????????????????????????B.?DE???????????????????????????????????????????C.?AD
2.如图,过点A的线段中(?
)线段最短.
A.?AC???????????????????????????????????????????B.?AB???????????????????????????????????????????C.?AD
3.一个三角形的两条边的长度分别是4厘米、5厘米,下列选项中能作为第三条边的长度的是(???
)。
A.?8厘米??????????????????????????????????????B.?9厘米??????????????????????????????????????C.?10厘米
4.下面(???
)组的三条线段能围成一个三角形。
A.?0.5cm、1cm、3cm??????????????????B.?1cm、2.5cm、3cm??????????????????C.?2cm、2cm、4cm
二、判断题
5.用三条线段肯定能围成一个三角形。(???
)
6.连接两点的所有线中,线段最短。(
)
7.任意三条线段都可以围成三角形。
(
)
8.钝角三角形只有一条高.(
??)
三、填空题
9.自行车的车架做成三角形,应用的是三角形具有________性。
10.三角形任意两边之和________第三边,两边之差________第三边。
11.一个三角形,第一条边长是6
cm,第二条边长是7
cm,第三条边长一定小于________cm。
12.图中有________个长方形?________个三角形?________个梯形?
四、解答题
13.写出下面每个三角形的名称,并画出每个三角形的高.
(1)
(2)
(3)
14.在不改变下面平行四边形木框形状的同时,使它变得稳定起来,画出示意图,并说说这样做的理由。
五、应用题
15.先画出如图底边上的高,再量出所需的数据(取整厘米数),求出它的面积.
参考答案
一、单选题
1.【答案】
A
【解析】【解答】点A到直线BC的距离是垂线段AE,
故答案为:A
【分析】直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
2.【答案】
A
【解析】【解答】解:图中过A点到直线BD的所有线段中,最短的一条是AC;
故选:A.
【分析】根据“点到直线的距离,垂线段最短”进行解答即可.解答此题应明确:点到直线的距离,垂线段最短.
3.【答案】
A
【解析】【解答】解:5-4<第三边<5+4
所以1厘米<第三边<9厘米,
所以8厘米符合。
故答案为:A。
【分析】三角形的三边关系:两边之和大于第三边,两边之差小于第三边,本题据此解答即可。
4.【答案】
B
【解析】【解答】选项A,因为0.5+1=1.5,1.5<3,所以0.5cm、1cm、3cm三条线段不能围成一个三角形;
选项B,因为1+2.5=3.5,3.5>3,3-1=2,2<2.5,所以1cm、2.5cm、3cm三条线段能围成一个三角形;
选项C,因为2+2=4,4=4,所以2cm、2cm、4cm三条线段不能围成一个三角形。
故答案为:B。
【分析】在三角形里,任意两边之和大于第三边,任意两边之差小于第三边,据此判断。
二、判断题
5.【答案】
错误
【解析】【解答】用三条线段不一定能围成一个三角形。原题说法错误。
故答案为:错误。
【分析】判断能不能围成三角形的方法:三角形两条短边之和必须大于第三边。
6.【答案】
正确
【解析】【解答】连接两点的所有线中,线段最短,此题说法正确.
故答案为:正确.
【分析】两点之间,线段最短,据此判断.
7.【答案】
错误
【解析】【解答】能围成三角形三边关系:任意两边之和都大于第三边。
【分析】三角形特征:两边之和大于第三边
8.【答案】
错误
【解析】【解答】解:任何三角形都有三个高,
钝角三角形也不例外,只不过它的高,一条在三角形内,两条在三角形外.
故答案为:错误.
【分析】三角形从它的任意顶点到对边都可以做一条高。
三、填空题
9.【答案】
稳定
【解析】【解答】解:自行车的车架做成三角形,应用的是三角形具有稳定性。
?故答案为:稳定。
【分析】三角形具有稳定性。
10.【答案】
大于;小于
【解析】【解答】三角形任意两边之和大于第三边,两边之差小于第三边。
故答案为:大于、小于
【分析】两边之差<三角形第三边的取值范围<两边之和。
11.【答案】
13
【解析】【解答】解:6+7=13(cm)。
故答案为:13。
【分析】三角形任意两边之和小于第三边,所以第三边的长度一定小于已知两条边的长度和。
12.【答案】
9;16;8
【解析】【解答】图中有9个长方形,16个三角形,8个梯形。
【分析】解答此题要根据长方形、三角形、梯形的特点,先数独立的图形,再数由独立的图形组合成的图形。
四、解答题
13.【答案】
(1)解:锐角三角形
(2)解:直角三角形
(3)解:钝角三角形
【解析】【分析】(1)锐角三角形;(2)直角三角形;(3)钝角三角形;画高时过三角形的一个顶点画出对边的垂线段,这条垂线段就是三角形的高.
14.【答案】
解:
【解析】【分析】根据三角形的稳定性可以把平行四边形的对角线连起来即可。
五、应用题
15.【答案】解:如图所示,即为所要求画的三角形已知底边上的高:
;
量得三角形的底约为4厘米,高约为2厘米,
则三角形的面积为:4×2÷2=4(平方厘米);
答:三角形的面积为4平方厘米
【解析】【分析】依据过直线外一点作已知直线的垂线的方法,即可作出已知底上的高;再据量得底和高的值,利用三角形的面积公式即可求其面积.此题主要考查:过直线外一点作已知直线的垂线的方法,以及三角形面积的计算方法.
