5.4-2抛体运动的规律--拓展-2020-2021学年【新教材】人教版(2019)高中物理必修第二册学案(word含答案)
文档属性
| 名称 | 5.4-2抛体运动的规律--拓展-2020-2021学年【新教材】人教版(2019)高中物理必修第二册学案(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 160.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-06-06 08:06:08 | ||
图片预览

文档简介
第4节 抛体运动的规律
第2课时
【学习目标】
1.运用平抛运动规律解决落点在斜面、墙面以及圆弧面上的平抛运动。
【知识梳理】
一、落点在斜面上的平抛运动
运用斜面倾角,找出斜面倾角与位移偏向角、速度偏向角的关系。常见的模型及处理方法如下:
图示
方法
基本规律
运动时间
分解速度,构建速度的矢量三角形
水平vx=v0
竖直vy=gt
合速度v=
由tan θ==得t=
分解位移,构建位移的矢量三角形
水平x=v0t
竖直y=gt2
合位移x合=
由tan θ==
得t=
在运动起点同时分解v0、g
由0=v1-a1t,
0-v=-2a1d
得t=,
d=
分解平行于斜面的速度v
由vy=gt
得t=
二、落点在竖直面上的平抛运动
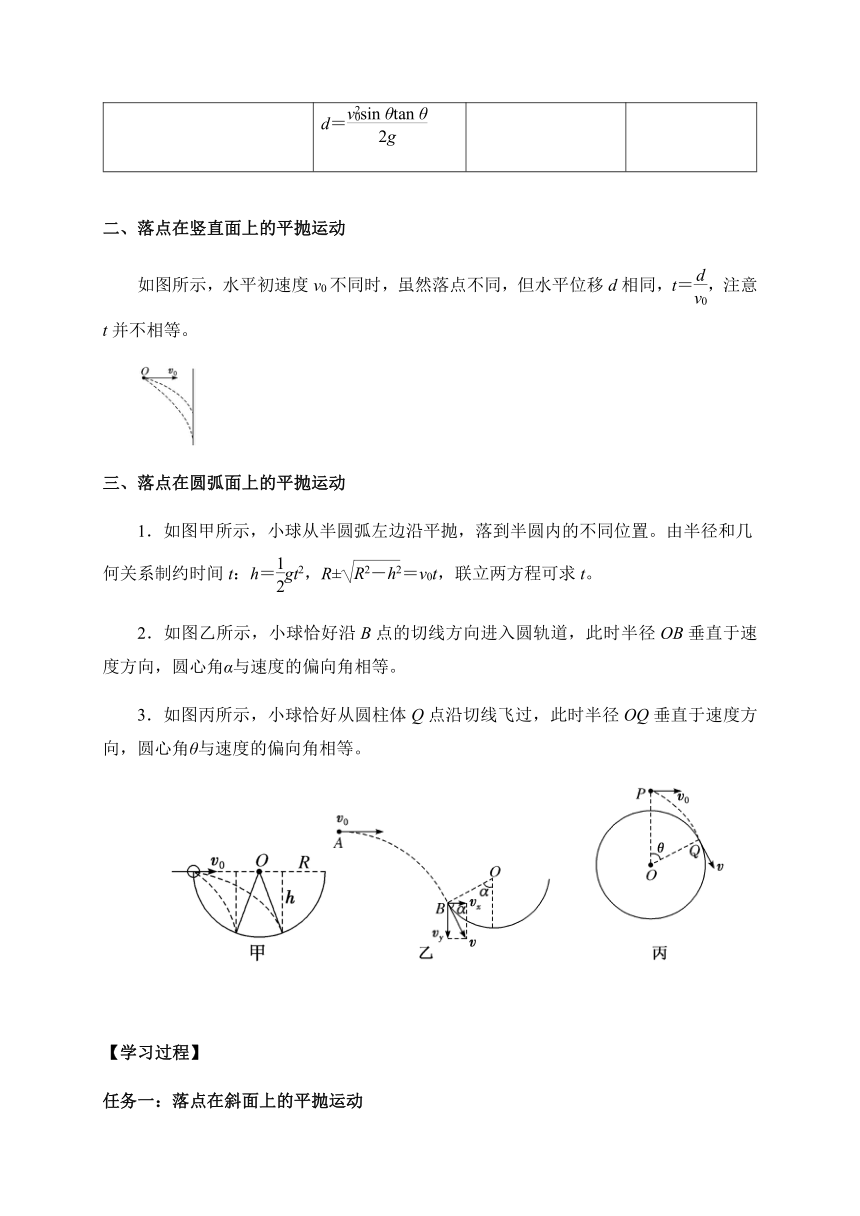
如图所示,水平初速度v0不同时,虽然落点不同,但水平位移d相同,t=,注意t并不相等。
三、落点在圆弧面上的平抛运动
1.如图甲所示,小球从半圆弧左边沿平抛,落到半圆内的不同位置。由半径和几何关系制约时间t:h=gt2,R±=v0t,联立两方程可求t。
2.如图乙所示,小球恰好沿B点的切线方向进入圆轨道,此时半径OB垂直于速度方向,圆心角α与速度的偏向角相等。
3.如图丙所示,小球恰好从圆柱体Q点沿切线飞过,此时半径OQ垂直于速度方向,圆心角θ与速度的偏向角相等。
【学习过程】
任务一:落点在斜面上的平抛运动
[练1] 跳台滑雪是一种勇敢者的滑雪运动,运动员穿专用滑雪板,在滑雪道上获得一定速度后从跳台飞出,在空中飞行一段距离后着陆。现有某运动员从跳台a 处沿水平方向飞出,在斜坡b 处着陆,如图5-5 所示。测得ab间的距离为40 m,斜坡与水平方向的夹角为30°,试计算运动员在a 处的速度大小和在空中飞行的时间。不计空气阻力,g 取10 m/s2。
[练2]在某次演习中,轰炸机沿水平方向投放了一枚炸弹,炸弹正好垂直击中山坡上的目标,山坡的倾角为θ,如图所示。不计空气阻力,求炸弹竖直方向下落的距离与水平方向通过的距离之比。
任务二:落点在竖直面上的平抛运动
[练3](多选)从竖直墙的前方A处,沿AO方向水平发射三颗弹丸a、b、c,在墙上留下的弹痕如图所示。已知Oa=ab=bc,则a、b、c三颗弹丸(不计空气阻力)( )
A.初速度之比是∶∶
B.初速度之比是1∶∶
C.从射出至打到墙上过程速度增量之比是1∶∶
D.从射出至打到墙上过程速度增量之比是∶∶
[练4]从同一点水平抛出三个小球分别撞在竖直墙壁上a点、b点、c点,则( )
A.落在a点的小球水平速度最小
B.落在b点的小球竖直速度最小
C.落在c点的小球飞行时间最短
D.a、b、c三点速度方向的反向延长线交于一点
任务三:落点在圆弧面上的平抛运动
[练5]如图为某娱乐节目中某个比赛环节的示意图,参与比赛的选手会遇到一个人造山谷AOB,AO是高h=3 m的竖直峭壁,OB是以A点为圆心的弧形坡,∠OAB=60°,B点右侧是一段水平跑道。选手可以自A点借助绳索降到O点后再爬上跑道,但身体素质好的选手会选择自A点直接跃上跑道。选手可视为质点,忽略空气阻力,重力加速度g取10 m/s2。
(1)若选手以速度v0水平跳出后,恰好能落到水平跑道上,求v0的最小值;
(2)若选手以速度v1=4 m/s水平跳出,求该选手在空中的运动时间。
[练6]如图,水平地面上有一个坑,其竖直截面为半圆.ab为沿水平方向的直径.若在a点以初速度v0沿ab方向抛出一小球,小球会击中坑壁上的c点.已知c点与水平地面的距离为圆半径的一半,求圆的半径.
【答案】
1.答案:10m/s 2s
2.答案:
3.答案: AC
4.答案: D
5.答案: (1) m/s (2)0.6 s
6.答案:R=
第2课时
【学习目标】
1.运用平抛运动规律解决落点在斜面、墙面以及圆弧面上的平抛运动。
【知识梳理】
一、落点在斜面上的平抛运动
运用斜面倾角,找出斜面倾角与位移偏向角、速度偏向角的关系。常见的模型及处理方法如下:
图示
方法
基本规律
运动时间
分解速度,构建速度的矢量三角形
水平vx=v0
竖直vy=gt
合速度v=
由tan θ==得t=
分解位移,构建位移的矢量三角形
水平x=v0t
竖直y=gt2
合位移x合=
由tan θ==
得t=
在运动起点同时分解v0、g
由0=v1-a1t,
0-v=-2a1d
得t=,
d=
分解平行于斜面的速度v
由vy=gt
得t=
二、落点在竖直面上的平抛运动
如图所示,水平初速度v0不同时,虽然落点不同,但水平位移d相同,t=,注意t并不相等。
三、落点在圆弧面上的平抛运动
1.如图甲所示,小球从半圆弧左边沿平抛,落到半圆内的不同位置。由半径和几何关系制约时间t:h=gt2,R±=v0t,联立两方程可求t。
2.如图乙所示,小球恰好沿B点的切线方向进入圆轨道,此时半径OB垂直于速度方向,圆心角α与速度的偏向角相等。
3.如图丙所示,小球恰好从圆柱体Q点沿切线飞过,此时半径OQ垂直于速度方向,圆心角θ与速度的偏向角相等。
【学习过程】
任务一:落点在斜面上的平抛运动
[练1] 跳台滑雪是一种勇敢者的滑雪运动,运动员穿专用滑雪板,在滑雪道上获得一定速度后从跳台飞出,在空中飞行一段距离后着陆。现有某运动员从跳台a 处沿水平方向飞出,在斜坡b 处着陆,如图5-5 所示。测得ab间的距离为40 m,斜坡与水平方向的夹角为30°,试计算运动员在a 处的速度大小和在空中飞行的时间。不计空气阻力,g 取10 m/s2。
[练2]在某次演习中,轰炸机沿水平方向投放了一枚炸弹,炸弹正好垂直击中山坡上的目标,山坡的倾角为θ,如图所示。不计空气阻力,求炸弹竖直方向下落的距离与水平方向通过的距离之比。
任务二:落点在竖直面上的平抛运动
[练3](多选)从竖直墙的前方A处,沿AO方向水平发射三颗弹丸a、b、c,在墙上留下的弹痕如图所示。已知Oa=ab=bc,则a、b、c三颗弹丸(不计空气阻力)( )
A.初速度之比是∶∶
B.初速度之比是1∶∶
C.从射出至打到墙上过程速度增量之比是1∶∶
D.从射出至打到墙上过程速度增量之比是∶∶
[练4]从同一点水平抛出三个小球分别撞在竖直墙壁上a点、b点、c点,则( )
A.落在a点的小球水平速度最小
B.落在b点的小球竖直速度最小
C.落在c点的小球飞行时间最短
D.a、b、c三点速度方向的反向延长线交于一点
任务三:落点在圆弧面上的平抛运动
[练5]如图为某娱乐节目中某个比赛环节的示意图,参与比赛的选手会遇到一个人造山谷AOB,AO是高h=3 m的竖直峭壁,OB是以A点为圆心的弧形坡,∠OAB=60°,B点右侧是一段水平跑道。选手可以自A点借助绳索降到O点后再爬上跑道,但身体素质好的选手会选择自A点直接跃上跑道。选手可视为质点,忽略空气阻力,重力加速度g取10 m/s2。
(1)若选手以速度v0水平跳出后,恰好能落到水平跑道上,求v0的最小值;
(2)若选手以速度v1=4 m/s水平跳出,求该选手在空中的运动时间。
[练6]如图,水平地面上有一个坑,其竖直截面为半圆.ab为沿水平方向的直径.若在a点以初速度v0沿ab方向抛出一小球,小球会击中坑壁上的c点.已知c点与水平地面的距离为圆半径的一半,求圆的半径.
【答案】
1.答案:10m/s 2s
2.答案:
3.答案: AC
4.答案: D
5.答案: (1) m/s (2)0.6 s
6.答案:R=
