5.4-1抛体运动的规律-2020-2021学年【新教材】人教版(2019)高中物理必修第二册学案(word含答案)
文档属性
| 名称 | 5.4-1抛体运动的规律-2020-2021学年【新教材】人教版(2019)高中物理必修第二册学案(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 304.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-06-06 08:10:55 | ||
图片预览




文档简介
第4节 抛体运动的规律
第1课时
【学习目标】
1.判断物体是否做抛体运动,理解抛体运动是匀变速运动。
2.理论分析并推导平抛运动规律。
3.运用平抛运动规律解决实际问题。
4.了解探究一般抛体运动规律的方法。
【问题导入】
在研究直线运动时,我们已经认识到,为了得到物体的速度与时间的关系,要先分析物体受到的力,由合力求出物体的加速度,进而得到物体的速度与时间的关系。关于平抛运动,我们是否可以遵循这样的思路,分别研究平抛运动相互垂直的两个分运动呢?
【知识梳理】
一、平抛运动
1.定义:将物体以一定的初速度沿水平方向抛出,物体只在重力作用下所做的运动。
2.性质:加速度为g的匀变速曲线运动。
3.条件:v0≠0,沿水平方向;只受重力作用。
4.研究方法:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
(1)水平方向:Fx=0,ax=0
(2)竖直方向:Fy=mg,ay=g
二、平抛运动的规律
1.平抛运动的速度
(1)水平方向:vx=v0
(2)竖直方向:vy=gt
(3)合速度大小:v==
(4)合速度方向:tanθ== (θ为v与水平方向的夹角).
2.平抛运动的位移
(1)水平方向:x=v0t
(2)竖直方向:y=gt2
(3)合位移大小:x合=,方向:tanα==(α为位移x合与水平方向的夹角)
提示:平抛运动的位移方向一定不会与某时刻的速度方向相同.
3.平抛运动的轨迹:y=x2,式中g和v0都是与x、y无关的常量,所以为常量,所以其运动轨迹是一条抛物线。
4.两个推论:
(1)做平抛运动的物体在任意时刻,总有tanθ=2tan α,注意θ≠2α;
(2)任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图C点。
5.平抛运动特点总结
(1)飞行时间:由t=知,飞行时间取决于下落高度h,与初速度v0无关。
(2)水平射程:x=v0t=v0,即水平射程由初速度v0和下落高度h共同决定。
(3)落地速度:实际落地速度(合速度),即v==,不是竖直方向速度vy。
(4)平抛运动的速度的变化规律
①任意时刻的速度水平分量均等于初速度v0。
②任意相等时间Δt内的速度变化量方向竖直向下,大小Δv=Δvy=gΔt。
(5)平抛运动的位移的变化规律
①任意相等时间Δt内,水平位移相同,即Δx=v0Δt。
②连续相等的时间Δt内,竖直方向上的位移差不变,即Δy=g(Δt)2。(逐差公式)
三、一般的抛体运动
1. 如果物体被抛出时的速度v0不沿水平方向,而是斜向上方或斜向下方,且只受重力的作用,这样的抛体运动称为斜抛.
2. 性质
斜抛运动可以看成是水平方向的匀速直线运动和竖直方向的竖直上抛或竖直下抛运动的合运动
3.基本规律(以斜上抛为例)
水平方向:Fx=0,v0x=v0cos θ,vx=v0cos θ
竖直方向:Fy=mg ,v0y=v0sin θ,vy=v0sin θ?gt。
4.技巧总结:斜抛运动问题多为斜上抛运动,可以在最高点分成两段处理,后半段为平抛运动,前半段的逆运动可以看成相等初速度的反向平抛运动。
【学习过程】
任务一:平抛运动的速度
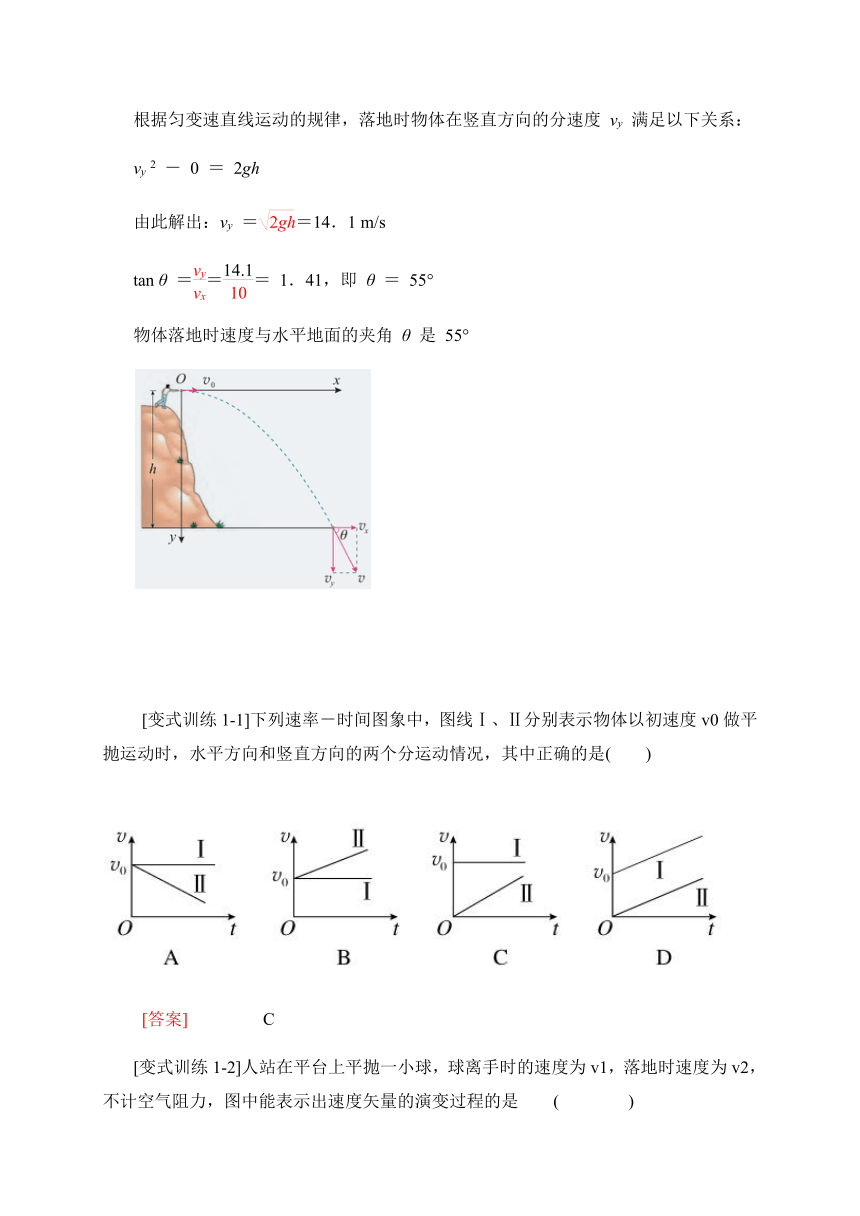
[例1]将一个物体以10ms的速度从10m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少?不计空气阻力,g取10m/s2。
[答案]以抛出时物体的位置 O 为原点,建立平面直角坐标系,x 轴沿初速度方向,y 轴竖直向下。
落地时,物体在水平方向的分速度:v x = v0 = 10 m/s
根据匀变速直线运动的规律,落地时物体在竖直方向的分速度 vy 满足以下关系:
vy 2 - 0 = 2gh
由此解出:vy ==14.1 m/s
tan θ === 1.41,即 θ = 55°
物体落地时速度与水平地面的夹角 θ 是 55°
[变式训练1-1]下列速率-时间图象中,图线Ⅰ、Ⅱ分别表示物体以初速度v0做平抛运动时,水平方向和竖直方向的两个分运动情况,其中正确的是( )
[答案] C
[变式训练1-2]人站在平台上平抛一小球,球离手时的速度为v1,落地时速度为v2,不计空气阻力,图中能表示出速度矢量的演变过程的是 ( )
[答案] C
任务二:平抛运动的位移与轨迹
[例2]某同学利用无人机玩“投弹”游戏。无人机以v0=2m/s的速度水平向右匀速飞行,在某时刻释放了一个小球。此时无人机到水平地面的距离h=20m,空气阻力忽略不计,g取10m/s。
(1)求小球下落的时间。(2)求小球释放点与落地点之间的水平距离。
[变式训练2-1]如图所示,射击枪水平放置,射击枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶之间的距离x=100 m,子弹射出的水平速度v=200 m/s,子弹从枪口射出的瞬间目标靶由静止开始释放,不计空气阻力,取重力加速度g为10 m/s2,求:
(1)从子弹由枪口射出开始计时,经多长时间子弹击中目标靶?
(2)目标靶由静止开始释放到被子弹击中,下落的距离h为多少?
答案:(1)0.5 s (2)1.25 m
任务三:斜抛运动
[例3]一个棒球以38 m/s的速度被击出,与水平方向的仰角为37°,求:
(1)该球上升达到的最大高度;(2)该球的飞行时间;(3)射程.(g取10 m/s2,sin37°=0.6)
斜抛运动水平方向分运动为匀速直线运动,竖直方向为竖直上抛运动.
[变式训练3-1]一门大炮的炮筒与水平面的夹角β=30°,当炮弹以初速度v0=300 m/s的速度发出,炮弹能否击中离大炮7500 m远的目标.(g取10 m/s2)
[答案] 不能击中
【巩固训练】
1. 用m、v0、h 分别表示平抛运动物体的质量、初速度和抛出点离水平地面的高度,不考虑空气阻力,以下物理量是由上述哪个或哪几个物理量决定的?为什么?
A. 物体在空中运动的时间
B. 物体在空中运动的水平位移
C. 物体落地时瞬时速度的大小
D. 物体落地时瞬时速度的方向
2. 如图所示,在水平桌面上用硬练习本做成一个斜面,使小钢球从斜面上某一位置滚下,钢球沿桌面飞出后做平抛运动。怎样用一把刻度尺测量钢球离开水平桌面时速度的大小?说出测量步骤,写出用所测的物理量表达速度的关系式。
3. 某卡车在限速60 km/h 的公路上与路旁障碍物相撞。处理事故的警察在泥地中发现一个小的金属物体,可以判断,它是车顶上一个松脱的零件,事故发生时被抛出而陷在泥里。警察测得这个零件在事故发生时的原位置与陷落点的水平距离为17.3 m,车顶距泥地的高度为2.45 m。请你根据这些数据为该车是否超速提供证据。
4. 某个质量为m 的物体在从静止开始下落的过程中,除了重力之外还受到水平方向大小、方向都不变的力F 的作用。
(1)求它在时刻 t 的水平分速度和竖直分速度。
(2)建立适当的坐标系,写出这个坐标系中代表物体运动轨迹的关系式。这个物体的运动轨迹是怎样的?
【答案】
1. A. 下落高度,t=
B. 下落高度和初速度,x=v0t=v0
C. 下落高度和初速度,v==
D. 下落高度和初速度,tanθ==
2.测量步骤如下。
①让小球从斜面上某一位置A无初速释放。
②测量小球在地面上的落点P与桌子边沿的水平距离x.
③测量小球在地面上的落点P与水平桌面竖直距离y.
可计算小球离开桌面的初速度v=x
3.该车已经超速。
零件做平抛运动,在竖直方向的位移y=gt2,则经历时间t===0.71s,水平方向位移x=vt=17. 3m.
零件做平抛运动的初速度v== m/s=24. 4 m/s=87. 8km/h>60 km/h,所以该车已经超速
4.(1)水平分速度vx=,竖直分速度,vy=gt
(2) y=x,,运动轨迹为一条直线
第1课时
【学习目标】
1.判断物体是否做抛体运动,理解抛体运动是匀变速运动。
2.理论分析并推导平抛运动规律。
3.运用平抛运动规律解决实际问题。
4.了解探究一般抛体运动规律的方法。
【问题导入】
在研究直线运动时,我们已经认识到,为了得到物体的速度与时间的关系,要先分析物体受到的力,由合力求出物体的加速度,进而得到物体的速度与时间的关系。关于平抛运动,我们是否可以遵循这样的思路,分别研究平抛运动相互垂直的两个分运动呢?
【知识梳理】
一、平抛运动
1.定义:将物体以一定的初速度沿水平方向抛出,物体只在重力作用下所做的运动。
2.性质:加速度为g的匀变速曲线运动。
3.条件:v0≠0,沿水平方向;只受重力作用。
4.研究方法:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
(1)水平方向:Fx=0,ax=0
(2)竖直方向:Fy=mg,ay=g
二、平抛运动的规律
1.平抛运动的速度
(1)水平方向:vx=v0
(2)竖直方向:vy=gt
(3)合速度大小:v==
(4)合速度方向:tanθ== (θ为v与水平方向的夹角).
2.平抛运动的位移
(1)水平方向:x=v0t
(2)竖直方向:y=gt2
(3)合位移大小:x合=,方向:tanα==(α为位移x合与水平方向的夹角)
提示:平抛运动的位移方向一定不会与某时刻的速度方向相同.
3.平抛运动的轨迹:y=x2,式中g和v0都是与x、y无关的常量,所以为常量,所以其运动轨迹是一条抛物线。
4.两个推论:
(1)做平抛运动的物体在任意时刻,总有tanθ=2tan α,注意θ≠2α;
(2)任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图C点。
5.平抛运动特点总结
(1)飞行时间:由t=知,飞行时间取决于下落高度h,与初速度v0无关。
(2)水平射程:x=v0t=v0,即水平射程由初速度v0和下落高度h共同决定。
(3)落地速度:实际落地速度(合速度),即v==,不是竖直方向速度vy。
(4)平抛运动的速度的变化规律
①任意时刻的速度水平分量均等于初速度v0。
②任意相等时间Δt内的速度变化量方向竖直向下,大小Δv=Δvy=gΔt。
(5)平抛运动的位移的变化规律
①任意相等时间Δt内,水平位移相同,即Δx=v0Δt。
②连续相等的时间Δt内,竖直方向上的位移差不变,即Δy=g(Δt)2。(逐差公式)
三、一般的抛体运动
1. 如果物体被抛出时的速度v0不沿水平方向,而是斜向上方或斜向下方,且只受重力的作用,这样的抛体运动称为斜抛.
2. 性质
斜抛运动可以看成是水平方向的匀速直线运动和竖直方向的竖直上抛或竖直下抛运动的合运动
3.基本规律(以斜上抛为例)
水平方向:Fx=0,v0x=v0cos θ,vx=v0cos θ
竖直方向:Fy=mg ,v0y=v0sin θ,vy=v0sin θ?gt。
4.技巧总结:斜抛运动问题多为斜上抛运动,可以在最高点分成两段处理,后半段为平抛运动,前半段的逆运动可以看成相等初速度的反向平抛运动。
【学习过程】
任务一:平抛运动的速度
[例1]将一个物体以10ms的速度从10m的高度水平抛出,落地时它的速度方向与水平地面的夹角θ是多少?不计空气阻力,g取10m/s2。
[答案]以抛出时物体的位置 O 为原点,建立平面直角坐标系,x 轴沿初速度方向,y 轴竖直向下。
落地时,物体在水平方向的分速度:v x = v0 = 10 m/s
根据匀变速直线运动的规律,落地时物体在竖直方向的分速度 vy 满足以下关系:
vy 2 - 0 = 2gh
由此解出:vy ==14.1 m/s
tan θ === 1.41,即 θ = 55°
物体落地时速度与水平地面的夹角 θ 是 55°
[变式训练1-1]下列速率-时间图象中,图线Ⅰ、Ⅱ分别表示物体以初速度v0做平抛运动时,水平方向和竖直方向的两个分运动情况,其中正确的是( )
[答案] C
[变式训练1-2]人站在平台上平抛一小球,球离手时的速度为v1,落地时速度为v2,不计空气阻力,图中能表示出速度矢量的演变过程的是 ( )
[答案] C
任务二:平抛运动的位移与轨迹
[例2]某同学利用无人机玩“投弹”游戏。无人机以v0=2m/s的速度水平向右匀速飞行,在某时刻释放了一个小球。此时无人机到水平地面的距离h=20m,空气阻力忽略不计,g取10m/s。
(1)求小球下落的时间。(2)求小球释放点与落地点之间的水平距离。
[变式训练2-1]如图所示,射击枪水平放置,射击枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶之间的距离x=100 m,子弹射出的水平速度v=200 m/s,子弹从枪口射出的瞬间目标靶由静止开始释放,不计空气阻力,取重力加速度g为10 m/s2,求:
(1)从子弹由枪口射出开始计时,经多长时间子弹击中目标靶?
(2)目标靶由静止开始释放到被子弹击中,下落的距离h为多少?
答案:(1)0.5 s (2)1.25 m
任务三:斜抛运动
[例3]一个棒球以38 m/s的速度被击出,与水平方向的仰角为37°,求:
(1)该球上升达到的最大高度;(2)该球的飞行时间;(3)射程.(g取10 m/s2,sin37°=0.6)
斜抛运动水平方向分运动为匀速直线运动,竖直方向为竖直上抛运动.
[变式训练3-1]一门大炮的炮筒与水平面的夹角β=30°,当炮弹以初速度v0=300 m/s的速度发出,炮弹能否击中离大炮7500 m远的目标.(g取10 m/s2)
[答案] 不能击中
【巩固训练】
1. 用m、v0、h 分别表示平抛运动物体的质量、初速度和抛出点离水平地面的高度,不考虑空气阻力,以下物理量是由上述哪个或哪几个物理量决定的?为什么?
A. 物体在空中运动的时间
B. 物体在空中运动的水平位移
C. 物体落地时瞬时速度的大小
D. 物体落地时瞬时速度的方向
2. 如图所示,在水平桌面上用硬练习本做成一个斜面,使小钢球从斜面上某一位置滚下,钢球沿桌面飞出后做平抛运动。怎样用一把刻度尺测量钢球离开水平桌面时速度的大小?说出测量步骤,写出用所测的物理量表达速度的关系式。
3. 某卡车在限速60 km/h 的公路上与路旁障碍物相撞。处理事故的警察在泥地中发现一个小的金属物体,可以判断,它是车顶上一个松脱的零件,事故发生时被抛出而陷在泥里。警察测得这个零件在事故发生时的原位置与陷落点的水平距离为17.3 m,车顶距泥地的高度为2.45 m。请你根据这些数据为该车是否超速提供证据。
4. 某个质量为m 的物体在从静止开始下落的过程中,除了重力之外还受到水平方向大小、方向都不变的力F 的作用。
(1)求它在时刻 t 的水平分速度和竖直分速度。
(2)建立适当的坐标系,写出这个坐标系中代表物体运动轨迹的关系式。这个物体的运动轨迹是怎样的?
【答案】
1. A. 下落高度,t=
B. 下落高度和初速度,x=v0t=v0
C. 下落高度和初速度,v==
D. 下落高度和初速度,tanθ==
2.测量步骤如下。
①让小球从斜面上某一位置A无初速释放。
②测量小球在地面上的落点P与桌子边沿的水平距离x.
③测量小球在地面上的落点P与水平桌面竖直距离y.
可计算小球离开桌面的初速度v=x
3.该车已经超速。
零件做平抛运动,在竖直方向的位移y=gt2,则经历时间t===0.71s,水平方向位移x=vt=17. 3m.
零件做平抛运动的初速度v== m/s=24. 4 m/s=87. 8km/h>60 km/h,所以该车已经超速
4.(1)水平分速度vx=,竖直分速度,vy=gt
(2) y=x,,运动轨迹为一条直线
