6.1-2传动装置模型 学案(word版含答案)
文档属性
| 名称 | 6.1-2传动装置模型 学案(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 235.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-06-06 08:14:58 | ||
图片预览

文档简介
第1节 圆周运动
第2课时 几种传动装置模型
【学习目标】
1.理解传动装置模型的特点,能够运用圆周运动的运动学公式解决实际问题。
【知识梳理】
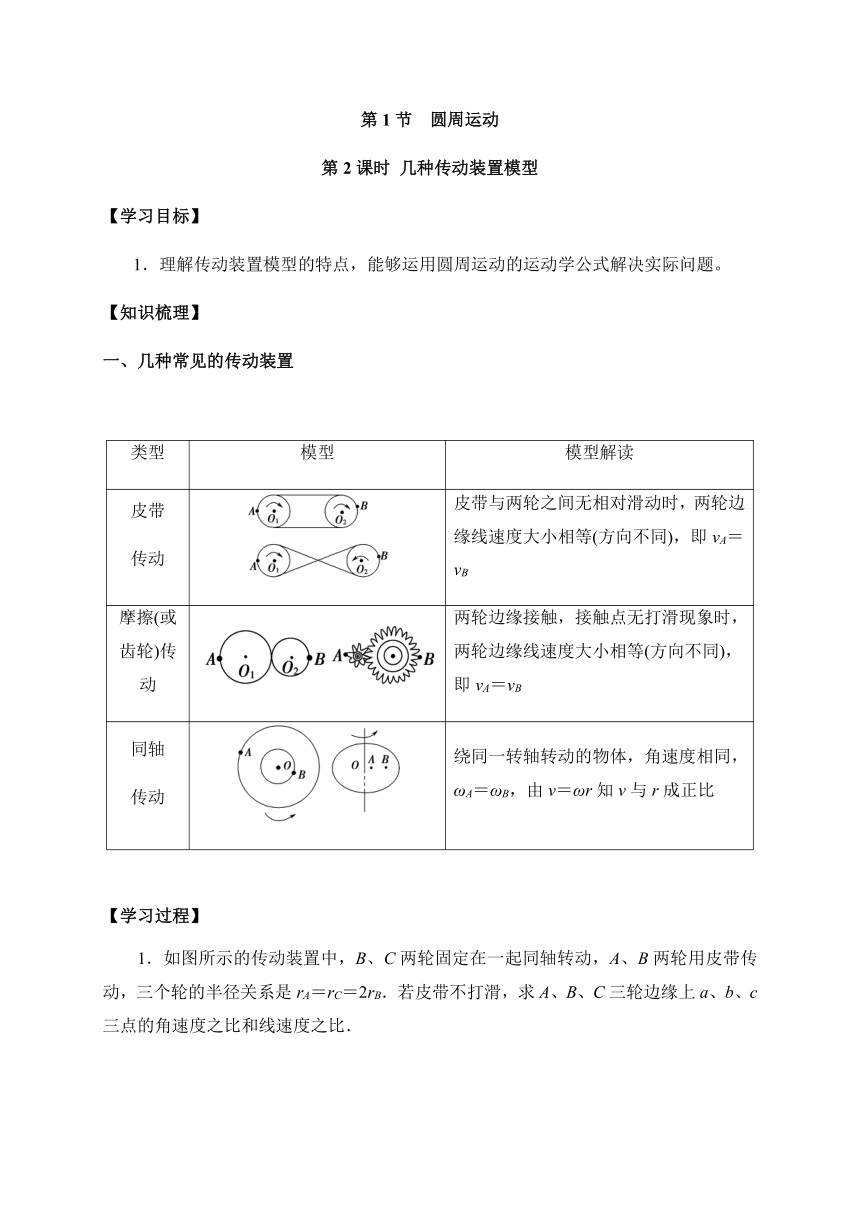
一、几种常见的传动装置
类型
模型
模型解读
皮带
传动
皮带与两轮之间无相对滑动时,两轮边缘线速度大小相等(方向不同),即vA=vB
摩擦(或齿轮)传动
两轮边缘接触,接触点无打滑现象时,两轮边缘线速度大小相等(方向不同),即vA=vB
同轴
传动
绕同一转轴转动的物体,角速度相同,ωA=ωB,由v=ωr知v与r成正比
【学习过程】
1.如图所示的传动装置中,B、C两轮固定在一起同轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB.若皮带不打滑,求A、B、C三轮边缘上a、b、c三点的角速度之比和线速度之比.
2.如图所示为皮带传动装置,主动轴O1上有两个半径分别为R和r的轮,O2上的轮半径为r′,已知R=2r, r′=R,设皮带不打滑,则( )
A. ωA∶ωB=1∶1 B. vA∶vB=1∶1
C. ωB∶ωC=1∶1 D. vB∶vC=1∶1
3. 如图所示是一个玩具陀螺,a、b和c是陀螺上的三个点. 当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是 ( )
A. a、b和c三点的线速度大小相等
B. a、b和c三点的角速度相等
C. a、b的角速度比c的大
D. c的线速度比a、b的大
4.如图所示,普通轮椅一般由轮椅架、车轮、刹车装置等组成.车轮有大车轮和小车轮,大车轮上固定有手轮圈,手轮圈由患者直接推动.已知大车轮、手轮圈、小车轮的半径之比为9∶8∶1,假设轮椅在地面上做直线运动,手和手轮圈之间、车轮和地面之间都不打滑,当手推手轮圈的角速度为ω时,小车轮的角速度为( )
A.ω B.ω C.ω D.9ω
【答案提示】
1.答案:1∶2∶2 1∶1∶2
2.答案:AD
3.答案:B
4.答案:D
第2课时 几种传动装置模型
【学习目标】
1.理解传动装置模型的特点,能够运用圆周运动的运动学公式解决实际问题。
【知识梳理】
一、几种常见的传动装置
类型
模型
模型解读
皮带
传动
皮带与两轮之间无相对滑动时,两轮边缘线速度大小相等(方向不同),即vA=vB
摩擦(或齿轮)传动
两轮边缘接触,接触点无打滑现象时,两轮边缘线速度大小相等(方向不同),即vA=vB
同轴
传动
绕同一转轴转动的物体,角速度相同,ωA=ωB,由v=ωr知v与r成正比
【学习过程】
1.如图所示的传动装置中,B、C两轮固定在一起同轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB.若皮带不打滑,求A、B、C三轮边缘上a、b、c三点的角速度之比和线速度之比.
2.如图所示为皮带传动装置,主动轴O1上有两个半径分别为R和r的轮,O2上的轮半径为r′,已知R=2r, r′=R,设皮带不打滑,则( )
A. ωA∶ωB=1∶1 B. vA∶vB=1∶1
C. ωB∶ωC=1∶1 D. vB∶vC=1∶1
3. 如图所示是一个玩具陀螺,a、b和c是陀螺上的三个点. 当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是 ( )
A. a、b和c三点的线速度大小相等
B. a、b和c三点的角速度相等
C. a、b的角速度比c的大
D. c的线速度比a、b的大
4.如图所示,普通轮椅一般由轮椅架、车轮、刹车装置等组成.车轮有大车轮和小车轮,大车轮上固定有手轮圈,手轮圈由患者直接推动.已知大车轮、手轮圈、小车轮的半径之比为9∶8∶1,假设轮椅在地面上做直线运动,手和手轮圈之间、车轮和地面之间都不打滑,当手推手轮圈的角速度为ω时,小车轮的角速度为( )
A.ω B.ω C.ω D.9ω
【答案提示】
1.答案:1∶2∶2 1∶1∶2
2.答案:AD
3.答案:B
4.答案:D
