6.4-3水平面内圆周运动 学案(word版含答案)
文档属性
| 名称 | 6.4-3水平面内圆周运动 学案(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 157.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-06-06 00:00:00 | ||
图片预览

文档简介
第4节 生活中的圆周运动
第3课时 水平面内圆周运动及临界值问题
【学习目标】
1.能够运用圆周运动规律解决水平面内圆周运动问题。
【知识梳理】
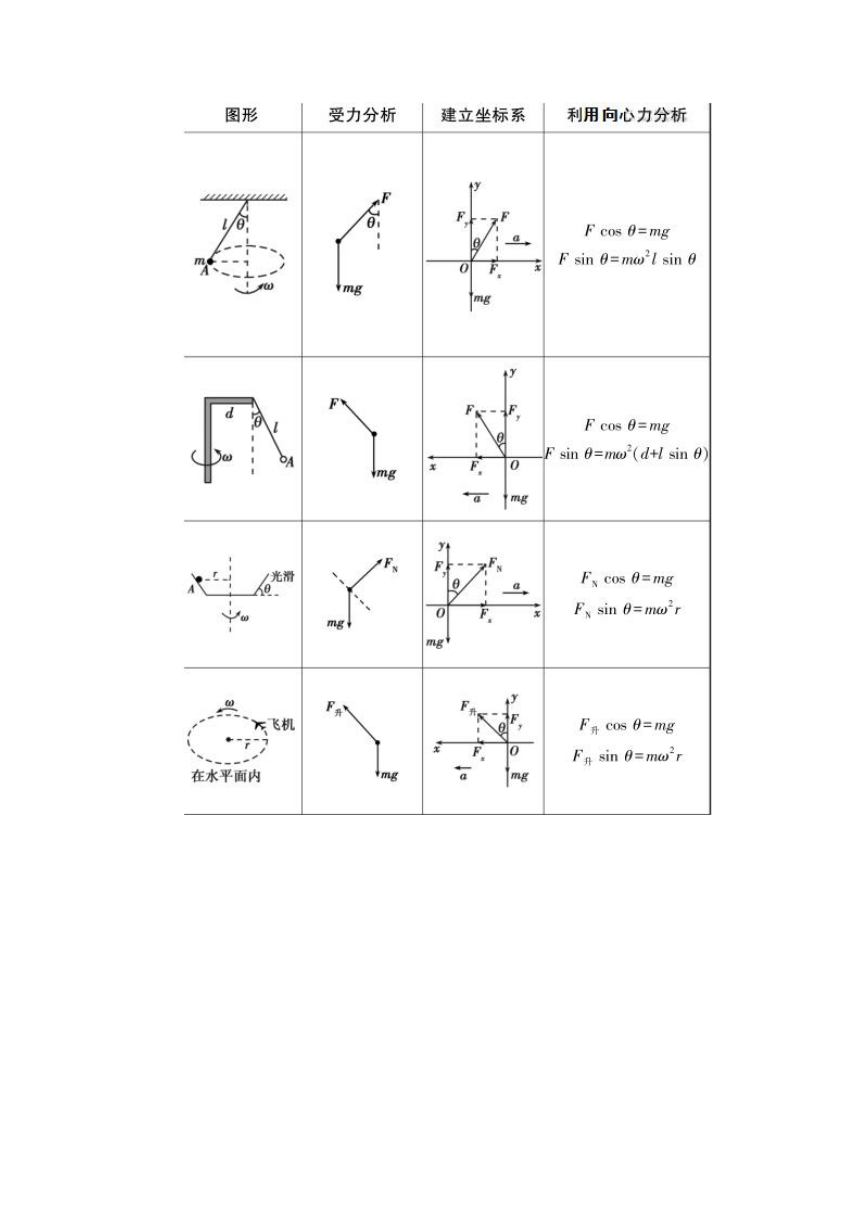
1.解答匀速圆周运动问题的一般步骤
(1)选择研究对象,找出匀速圆周运动的圆心和半径。
(2)分析物体受力情况,其合外力提供向心力。
(3)由Fn=m或Fn=mrω2或Fn=mr列方程求解。
2.常见模型
3.水平面内圆周运动的三种临界情况
(1)接触与脱离的临界条件:两物体相接触或脱离的临界条件是:弹力FN=0。
(2)相对滑动的临界条件:两物体相接触且处于相对静止时,常存在着静摩擦力,则相对滑动的临界条件是:静摩擦力达到最大值。
(3)绳子断裂与松弛的临界条件:绳子所能承受的张力是有限度的,绳子断与不断的临界条件是绳中张力等于它所能承受的最大张力,绳子松弛的临界条件是:FT=0。
【学习过程】
1.如图所示,转动轴垂直于光滑水平面,交点O的上方h(A点)处固定细绳的一端,细绳的另一端拴接一质量为m的小球B,绳长l大于h,转动轴带动小球在光滑水平面上做圆周运动。当转动的角速度ω逐渐增大时,下列说法正确的是( )
A.小球始终受三个力的作用
B.细绳上的拉力始终保持不变
C.要使球不离开水平面,角速度的最大值为
D.若小球飞离了水平面,则角速度可能为
2.如图所示,两绳系一质量为m=0.1 kg的小球,上面绳长L=2 m,两端都拉直时与轴的夹角分别为30°与45°,问球的角速度在什么范围内,两绳始终伸直?
3.如图所示,质量为m的物体A距转盘中心距离为r,物体A与转盘的最大静摩擦力为其重力的μ倍,欲使A物体与转盘相对静止,转盘匀速转动的最大角速度不能超过多少?
4.如图所示,水平转盘上放有质量为m的物块,当物块到转轴的距离为r时,连接物块和转轴的绳刚好被拉直(绳上张力为零).物体和转盘间最大静摩擦力是其正压力的μ倍,求:
(1)当转盘的角速度ω1=时,细绳的拉力F1.
(2)当转盘的角速度ω2=时,细绳的拉力F2.
【答案提示】
1.答案:C
2.答案:2.40 rad/s≤ω≤3.16 rad/s
3.答案:ω=
4.答案:(1)0 (2)
第3课时 水平面内圆周运动及临界值问题
【学习目标】
1.能够运用圆周运动规律解决水平面内圆周运动问题。
【知识梳理】
1.解答匀速圆周运动问题的一般步骤
(1)选择研究对象,找出匀速圆周运动的圆心和半径。
(2)分析物体受力情况,其合外力提供向心力。
(3)由Fn=m或Fn=mrω2或Fn=mr列方程求解。
2.常见模型
3.水平面内圆周运动的三种临界情况
(1)接触与脱离的临界条件:两物体相接触或脱离的临界条件是:弹力FN=0。
(2)相对滑动的临界条件:两物体相接触且处于相对静止时,常存在着静摩擦力,则相对滑动的临界条件是:静摩擦力达到最大值。
(3)绳子断裂与松弛的临界条件:绳子所能承受的张力是有限度的,绳子断与不断的临界条件是绳中张力等于它所能承受的最大张力,绳子松弛的临界条件是:FT=0。
【学习过程】
1.如图所示,转动轴垂直于光滑水平面,交点O的上方h(A点)处固定细绳的一端,细绳的另一端拴接一质量为m的小球B,绳长l大于h,转动轴带动小球在光滑水平面上做圆周运动。当转动的角速度ω逐渐增大时,下列说法正确的是( )
A.小球始终受三个力的作用
B.细绳上的拉力始终保持不变
C.要使球不离开水平面,角速度的最大值为
D.若小球飞离了水平面,则角速度可能为
2.如图所示,两绳系一质量为m=0.1 kg的小球,上面绳长L=2 m,两端都拉直时与轴的夹角分别为30°与45°,问球的角速度在什么范围内,两绳始终伸直?
3.如图所示,质量为m的物体A距转盘中心距离为r,物体A与转盘的最大静摩擦力为其重力的μ倍,欲使A物体与转盘相对静止,转盘匀速转动的最大角速度不能超过多少?
4.如图所示,水平转盘上放有质量为m的物块,当物块到转轴的距离为r时,连接物块和转轴的绳刚好被拉直(绳上张力为零).物体和转盘间最大静摩擦力是其正压力的μ倍,求:
(1)当转盘的角速度ω1=时,细绳的拉力F1.
(2)当转盘的角速度ω2=时,细绳的拉力F2.
【答案提示】
1.答案:C
2.答案:2.40 rad/s≤ω≤3.16 rad/s
3.答案:ω=
4.答案:(1)0 (2)
