山西省2020-2021学年高一下学期5月联合考试数学试题 Word版含答案解析
文档属性
| 名称 | 山西省2020-2021学年高一下学期5月联合考试数学试题 Word版含答案解析 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 21:19:01 | ||
图片预览




文档简介
2020~2021年山西省高一下学期5月联合考试(B)
数学
考生注意:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.
2.请将各题答案填写在答题卡上.
3.本试卷主要考试内容:人教A版必修第一册占20%,必修第二册第六、七章占30%,第八、九章占50%
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知复数false,则false
A.false B.false C.false D.false
2. 已知a>0>b,则下列不等式一定成立的是
A.false B.false C.false D.false
3. 已知某中学有学生3600人,其中男生2000人,为了解该校学生身高情况,现用分层抽样法从该校随机抽取270人进行调查,其中女生应抽取的人数是
A. 90 B. 120 C. 150 D. 180
4. 在△ABC中,角A,B,C所对的边分别是a,b,c,则"false"是"cos AA.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
5. 已知函数false是定义在(-1,1)上的奇函数,则false
A.3 B.1 C.false D.false
6. 已知复数false 是方程false的一个根,则false
A.false B.false C.3 D.5
7. 在长方体false中,底而ABCD是正方形,异面直线AB与false所成角的大小为false,则该长方体的侧面积与表面积的比值是
A.false B.false C.false D.false
8. 已知某校有高中学生6000人,该校高中年级的学生人数和肥胖情况分别如图1和图2所示.
下列说法正确的是
A. 高一年级的学生肥胖人数最多
B. 高三年级的学生肥胖人数最少
C. 高一年级的学生肥胖人数与高二年级的学生肥胖人数相同
D. 该校所有高中学生的肥胖率是12%
9. 将函数false图象上所有的点向右平移false 个单位长度后,得到函数falsefalse的图象,若函数false,则下列结论正确的是
A. false的最大值是2
B. false 的图象关于直线false对称
C.false 的最小正周期是false
D.false的单调递增区间是false
10. 如图,在正四棱锥P-ABCD中,false,从A拉一条细绳绕过侧棱PB和PC到达D点,则细绳的最短长度为
A.false B.false C.false D.false
11. 某校组织了一场演讲比赛,五位评委对某位参赛选手的评分分别为90,x,98,y,91.已知这组数据的平均数为95,方差为15.2,则false
A.2 B.4 C.5 D.6
12. 如图,在正方体false中,AB=2,E为棱BC的中点,F为棱false上的一动点,过点A,E,F作该正方体的截面,则该截面不可能是
A. 平行四边形 B. 等腰梯形 C. 五边形 D. 六边形
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡中的横线上.
13. 已知向量false,则a,b的夹角是 .
14. 顾客满意度指数是根据顾客对企业产品和服务质量的评价,通过建立模型计算而获得的一个指数,是一个测量顾客满意程度的经济指标,常用区间[0,10]内的一个数来表示,该数越大表示满意程度越高,现某商场随机抽取9名顾客进行调查,得到他们的满意度指数分别为 6,9,7,4,8,9,9,7,5,则这组数据的第70百分位数是 .
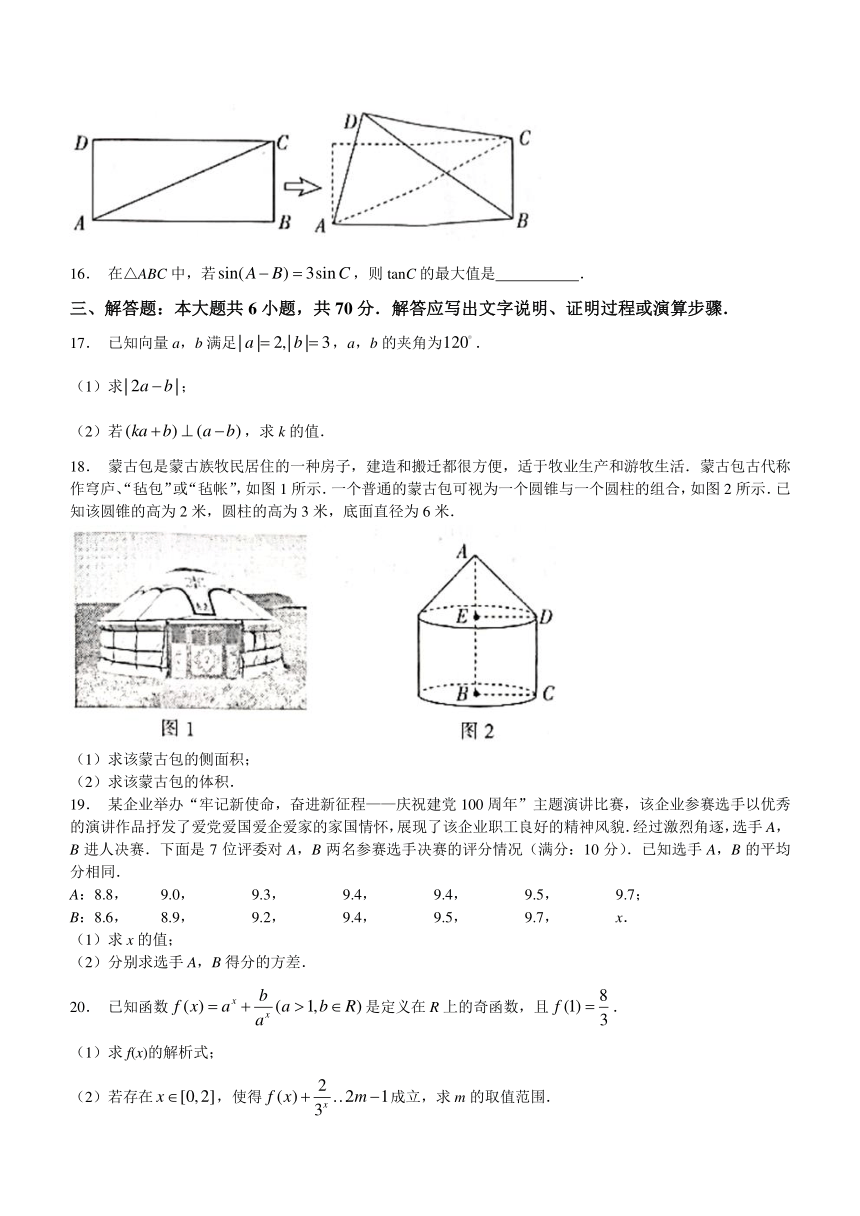
15. 如图,在矩形ABCD中,false.现将△ACD沿AC折起,得到如图所示的三棱锥D-ABC,则该三棱锥体积的最大值是 ,此时,其内切球的半径是 .
16. 在△ABC中,若false,则tanC的最大值是 .
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知向量a,b满足false,a,b的夹角为false.
(1)求false;
(2)若false,求k的值.
18. 蒙古包是蒙古族牧民居住的一种房子,建造和搬迁都很方便,适于牧业生产和游牧生活.蒙古包古代称作穹庐、“毡包”或“毡帐”,如图1所示.一个普通的蒙古包可视为一个圆锥与一个圆柱的组合,如图2所示.已知该圆锥的高为2米,圆柱的高为3米,底面直径为6米.
(1)求该蒙古包的侧面积;
(2)求该蒙古包的体积.
19. 某企业举办“牢记新使命,奋进新征程——庆祝建党100周年”主题演讲比赛,该企业参赛选手以优秀的演讲作品抒发了爱党爱国爱企爱家的家国情怀,展现了该企业职工良好的精神风貌.经过激烈角逐,选手A,B进人决赛.下面是7位评委对A,B两名参赛选手决赛的评分情况(满分:10分).已知选手A,B的平均分相同.
A:8.8, 9.0, 9.3, 9.4, 9.4, 9.5, 9.7;
B:8.6, 8.9, 9.2, 9.4, 9.5, 9.7, x.
(1)求x的值;
(2)分别求选手A,B得分的方差.
20. 已知函数false是定义在R上的奇函数,且false.
(1)求f(x)的解析式;
(2)若存在false,使得false成立,求m的取值范围.
21. 某社区规划在小区内建立一个如图所示的圆形休闲区,经调研确定,该圆内接四边形ABCD为儿童娱乐设施建筑用地,AB=AD=2CD=6,BC=9.
(1)求儿童娱乐设施建筑用地的面积
(2)若A,C,D不动,在圆弧false 上取一点E,使得儿童娱乐设施的新建筑用地AECD的面积最大,并求出最大值.
22. 如图,在四棱柱false中,四边形ABCD为正方形,各棱长均为1,falsefalse.
(1)证明:false;
(2)若false,侧棱false上是否存在一点E,使得false与平面false所成角的正弦值为false?若存在,求出false的长度;若不存在,请说明理由.
2020~2021学年山西省高一下学期5月联合考试(B)
数学参考答案
1.A因为false,所以false,
则false.
2.C当false时,false,则A错误;
因为false,所以false,所以false ,则B错误;
因为false,所以false,则C正确;
当c=0时,false,则D错误.
3.B由题意可得女生应抽取的人数是false.
4.A由a>b,得A>B,则cos A由cos AB,则a>b.
5.D由题意可得false,解得false.
经检验当a=2时,f(x)是定义在(-1,1)上的奇函数,
则 false ,故false.
6.B由题意可得false,
即false,
则false,解得afalse,
故false.
7.C连接false(图略),因为false,
所以false是异面直线AB与false所成的角,即 false.
设false,在false中false,
则false,整理得false,
从而该长方体的侧面积false,
该长方体的表面积false,
故false.
8.A由题意可得该校高一年级的学生人数为false,
肥胖人数为false;
高二年级的学生人数为false,
肥胖人数为false;
高三年级的学生人数为falsefalse,
肥胜人数为false,
则A正确,B,C错误;
该校所有高中学生的肥胖率是falsefalse,则D错误.
9.D 由题意可得false,
则false,
则falsefalse
falsefalse,
故false的最大值是false,false的最小正周期是false ,A,C错误.
令false ,解得false.
由false,得false,则B错误.
令false,解得false,
即f(x)的单调递增区间是false,则D正确.
10. C如图,将侧而PAB,侧而PBC,侧而PCD展开到一个平面内,
由题意可知PA=PB=PC=PD=5, AB=BC=CD=5,false.
设false,则false ,
从而false.由二倍角公式可得false ,falsefalse,
则false.
由余弦定理可得false,
则false,即细绳的最短长度为false.
11. B由题意可得false,
整理得false,
设false,则false,
即falsefalse,解得false,故false.
12. D当false,即F与false重合时,如图1,取false的中点,截面为矩形false ;
当false时,如图2,截面为平行四边形AEGF;
当false时,如图3,截面为五边形AEGHF,
当false,即F与false重合时,如图4,截面为等腰梯形AEGF.
13.false 由题意可得false,false,
则false,故向量a,b的夹角是false.
14. 9该组数据从小到大排列为4,5,6,7,7,8,9,9,9.
因为false,所以这组数据的第70百分位数是9.
15.false;false 由题意可知当平面ACD⊥平面ABC时,三棱锥D-ABC的体积最大.
如图,作DE⊥AC,垂足为E,连接BE.因false,所以false,
DE=2,则该三楼锥体积的最大值false.
此时,AE=1,false,false,
则 false,
从而false.因为AB=false,
所以false,
所以false,
则△ABD的面积为falsefalse,
故三棱锥D-ABC的表面积false.
设三棱锥D-ABC内切球的半径为r,
则false,即false,解得false.
16. false因为sin(A-B)=3sin C,
所以sin Acos B-cos Asin B=3(sin Acos B+cos Asin B),
所以sin Acos B=-2cos Asin B,即tan A=-2tan B.
因为false,
所以falsefalsefalse.
因为false,所以false,
所以tan C>0,所以tan B>0,
所以falsefalse,
则false,
当且仅当false时,等号成立.
17. 解:由题意可得false.
(1)因为false,
所以false.
(2)由题意可得false,即false,
则false,解得false.
18. 解:由题意可知BC=DE=3米,AE=2米,BE=3米,false米.
(1)圆锥部分的侧面积false平方米.
圆柱部分的侧面积false平方米.
故该蒙古包的侧面积false平方米.
(2)圆锥部分的体积false立方米
圆柱部分的体积false立方米.
故该蒙古包的体积false立方米.
19.解:(1)false,
false.
因为false,所以false,解得x=9.8.
(2)由(1)可知false.
则false,
false
false.
20. 解:(1)因为f(x)是奇函数,所以f(0)=1+b=0,所以false.
因为false,所以false,
所以false,即false,
解得false或false(舍去)
故false.
(2)设false,因为false,所以false.
令false,对任意false,且false,
则false.
因为false,所以false ,所以false .
因为false,所以false,所以false,
即false,则g(t)在[1,9]上单调递增,
故false.
false等价于false,
则false,解得false,故m的取值范围为false.
21. 解:(1)连接AC(图略),由题意可得false ,
则false.①
由余弦定理可得false,
则false.②
由①②可得false,从而false.
故四边形ABCD的面积为
falsefalse.
(2)由余弦定理可得false.
由(1)可得false,
由余弦定理可得false,则false,
从而△AEC的面积false.
由(1)可知△ACD的面积为false ,
则儿童娱乐设施的新建筑用地AECD的面积为false.
22.(1)证明:如图,连接false 记false,连接false.
因为false ,
所以false.
因为四边形ABCD为正方形,所以O为false的中点,
所以false.
因为四边形ABCD为正方形,所以.
因为false平面false,false平面false,且false,
所以false平面false.
因为false平面false,所以false.
(2)解:连接false.
因为四边形ABCD是边长为1的正方形,
所以false.
因为false,且false,所以false.
由(1)可知false,所以false,
所以false,则false,且false.
因为false平面false,false平面false,且false,
所以false平面false.
设点false到平面false的距离为false.
因为false,所以false,
解得false.
因为false平面false,所以点E到平面false的距离为false.
假设存在满足条件的点E,则false,即false.
过E作EF⊥false,垂足为F,连接false,
则点F在false的延长线上,false.
设false,则false,
从而false,解得false.
因为点E在棱false 上,所以false,所以假设不成立,
即不存在点E,使得false与平面false所成角的正弦值为false.
数学
考生注意:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.
2.请将各题答案填写在答题卡上.
3.本试卷主要考试内容:人教A版必修第一册占20%,必修第二册第六、七章占30%,第八、九章占50%
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 已知复数false,则false
A.false B.false C.false D.false
2. 已知a>0>b,则下列不等式一定成立的是
A.false B.false C.false D.false
3. 已知某中学有学生3600人,其中男生2000人,为了解该校学生身高情况,现用分层抽样法从该校随机抽取270人进行调查,其中女生应抽取的人数是
A. 90 B. 120 C. 150 D. 180
4. 在△ABC中,角A,B,C所对的边分别是a,b,c,则"false"是"cos A
C.必要不充分条件 D.既不充分也不必要条件
5. 已知函数false是定义在(-1,1)上的奇函数,则false
A.3 B.1 C.false D.false
6. 已知复数false 是方程false的一个根,则false
A.false B.false C.3 D.5
7. 在长方体false中,底而ABCD是正方形,异面直线AB与false所成角的大小为false,则该长方体的侧面积与表面积的比值是
A.false B.false C.false D.false
8. 已知某校有高中学生6000人,该校高中年级的学生人数和肥胖情况分别如图1和图2所示.
下列说法正确的是
A. 高一年级的学生肥胖人数最多
B. 高三年级的学生肥胖人数最少
C. 高一年级的学生肥胖人数与高二年级的学生肥胖人数相同
D. 该校所有高中学生的肥胖率是12%
9. 将函数false图象上所有的点向右平移false 个单位长度后,得到函数falsefalse的图象,若函数false,则下列结论正确的是
A. false的最大值是2
B. false 的图象关于直线false对称
C.false 的最小正周期是false
D.false的单调递增区间是false
10. 如图,在正四棱锥P-ABCD中,false,从A拉一条细绳绕过侧棱PB和PC到达D点,则细绳的最短长度为
A.false B.false C.false D.false
11. 某校组织了一场演讲比赛,五位评委对某位参赛选手的评分分别为90,x,98,y,91.已知这组数据的平均数为95,方差为15.2,则false
A.2 B.4 C.5 D.6
12. 如图,在正方体false中,AB=2,E为棱BC的中点,F为棱false上的一动点,过点A,E,F作该正方体的截面,则该截面不可能是
A. 平行四边形 B. 等腰梯形 C. 五边形 D. 六边形
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卡中的横线上.
13. 已知向量false,则a,b的夹角是 .
14. 顾客满意度指数是根据顾客对企业产品和服务质量的评价,通过建立模型计算而获得的一个指数,是一个测量顾客满意程度的经济指标,常用区间[0,10]内的一个数来表示,该数越大表示满意程度越高,现某商场随机抽取9名顾客进行调查,得到他们的满意度指数分别为 6,9,7,4,8,9,9,7,5,则这组数据的第70百分位数是 .
15. 如图,在矩形ABCD中,false.现将△ACD沿AC折起,得到如图所示的三棱锥D-ABC,则该三棱锥体积的最大值是 ,此时,其内切球的半径是 .
16. 在△ABC中,若false,则tanC的最大值是 .
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知向量a,b满足false,a,b的夹角为false.
(1)求false;
(2)若false,求k的值.
18. 蒙古包是蒙古族牧民居住的一种房子,建造和搬迁都很方便,适于牧业生产和游牧生活.蒙古包古代称作穹庐、“毡包”或“毡帐”,如图1所示.一个普通的蒙古包可视为一个圆锥与一个圆柱的组合,如图2所示.已知该圆锥的高为2米,圆柱的高为3米,底面直径为6米.
(1)求该蒙古包的侧面积;
(2)求该蒙古包的体积.
19. 某企业举办“牢记新使命,奋进新征程——庆祝建党100周年”主题演讲比赛,该企业参赛选手以优秀的演讲作品抒发了爱党爱国爱企爱家的家国情怀,展现了该企业职工良好的精神风貌.经过激烈角逐,选手A,B进人决赛.下面是7位评委对A,B两名参赛选手决赛的评分情况(满分:10分).已知选手A,B的平均分相同.
A:8.8, 9.0, 9.3, 9.4, 9.4, 9.5, 9.7;
B:8.6, 8.9, 9.2, 9.4, 9.5, 9.7, x.
(1)求x的值;
(2)分别求选手A,B得分的方差.
20. 已知函数false是定义在R上的奇函数,且false.
(1)求f(x)的解析式;
(2)若存在false,使得false成立,求m的取值范围.
21. 某社区规划在小区内建立一个如图所示的圆形休闲区,经调研确定,该圆内接四边形ABCD为儿童娱乐设施建筑用地,AB=AD=2CD=6,BC=9.
(1)求儿童娱乐设施建筑用地的面积
(2)若A,C,D不动,在圆弧false 上取一点E,使得儿童娱乐设施的新建筑用地AECD的面积最大,并求出最大值.
22. 如图,在四棱柱false中,四边形ABCD为正方形,各棱长均为1,falsefalse.
(1)证明:false;
(2)若false,侧棱false上是否存在一点E,使得false与平面false所成角的正弦值为false?若存在,求出false的长度;若不存在,请说明理由.
2020~2021学年山西省高一下学期5月联合考试(B)
数学参考答案
1.A因为false,所以false,
则false.
2.C当false时,false,则A错误;
因为false,所以false,所以false ,则B错误;
因为false,所以false,则C正确;
当c=0时,false,则D错误.
3.B由题意可得女生应抽取的人数是false.
4.A由a>b,得A>B,则cos A
5.D由题意可得false,解得false.
经检验当a=2时,f(x)是定义在(-1,1)上的奇函数,
则 false ,故false.
6.B由题意可得false,
即false,
则false,解得afalse,
故false.
7.C连接false(图略),因为false,
所以false是异面直线AB与false所成的角,即 false.
设false,在false中false,
则false,整理得false,
从而该长方体的侧面积false,
该长方体的表面积false,
故false.
8.A由题意可得该校高一年级的学生人数为false,
肥胖人数为false;
高二年级的学生人数为false,
肥胖人数为false;
高三年级的学生人数为falsefalse,
肥胜人数为false,
则A正确,B,C错误;
该校所有高中学生的肥胖率是falsefalse,则D错误.
9.D 由题意可得false,
则false,
则falsefalse
falsefalse,
故false的最大值是false,false的最小正周期是false ,A,C错误.
令false ,解得false.
由false,得false,则B错误.
令false,解得false,
即f(x)的单调递增区间是false,则D正确.
10. C如图,将侧而PAB,侧而PBC,侧而PCD展开到一个平面内,
由题意可知PA=PB=PC=PD=5, AB=BC=CD=5,false.
设false,则false ,
从而false.由二倍角公式可得false ,falsefalse,
则false.
由余弦定理可得false,
则false,即细绳的最短长度为false.
11. B由题意可得false,
整理得false,
设false,则false,
即falsefalse,解得false,故false.
12. D当false,即F与false重合时,如图1,取false的中点,截面为矩形false ;
当false时,如图2,截面为平行四边形AEGF;
当false时,如图3,截面为五边形AEGHF,
当false,即F与false重合时,如图4,截面为等腰梯形AEGF.
13.false 由题意可得false,false,
则false,故向量a,b的夹角是false.
14. 9该组数据从小到大排列为4,5,6,7,7,8,9,9,9.
因为false,所以这组数据的第70百分位数是9.
15.false;false 由题意可知当平面ACD⊥平面ABC时,三棱锥D-ABC的体积最大.
如图,作DE⊥AC,垂足为E,连接BE.因false,所以false,
DE=2,则该三楼锥体积的最大值false.
此时,AE=1,false,false,
则 false,
从而false.因为AB=false,
所以false,
所以false,
则△ABD的面积为falsefalse,
故三棱锥D-ABC的表面积false.
设三棱锥D-ABC内切球的半径为r,
则false,即false,解得false.
16. false因为sin(A-B)=3sin C,
所以sin Acos B-cos Asin B=3(sin Acos B+cos Asin B),
所以sin Acos B=-2cos Asin B,即tan A=-2tan B.
因为false,
所以falsefalsefalse.
因为false,所以false,
所以tan C>0,所以tan B>0,
所以falsefalse,
则false,
当且仅当false时,等号成立.
17. 解:由题意可得false.
(1)因为false,
所以false.
(2)由题意可得false,即false,
则false,解得false.
18. 解:由题意可知BC=DE=3米,AE=2米,BE=3米,false米.
(1)圆锥部分的侧面积false平方米.
圆柱部分的侧面积false平方米.
故该蒙古包的侧面积false平方米.
(2)圆锥部分的体积false立方米
圆柱部分的体积false立方米.
故该蒙古包的体积false立方米.
19.解:(1)false,
false.
因为false,所以false,解得x=9.8.
(2)由(1)可知false.
则false,
false
false.
20. 解:(1)因为f(x)是奇函数,所以f(0)=1+b=0,所以false.
因为false,所以false,
所以false,即false,
解得false或false(舍去)
故false.
(2)设false,因为false,所以false.
令false,对任意false,且false,
则false.
因为false,所以false ,所以false .
因为false,所以false,所以false,
即false,则g(t)在[1,9]上单调递增,
故false.
false等价于false,
则false,解得false,故m的取值范围为false.
21. 解:(1)连接AC(图略),由题意可得false ,
则false.①
由余弦定理可得false,
则false.②
由①②可得false,从而false.
故四边形ABCD的面积为
falsefalse.
(2)由余弦定理可得false.
由(1)可得false,
由余弦定理可得false,则false,
从而△AEC的面积false.
由(1)可知△ACD的面积为false ,
则儿童娱乐设施的新建筑用地AECD的面积为false.
22.(1)证明:如图,连接false 记false,连接false.
因为false ,
所以false.
因为四边形ABCD为正方形,所以O为false的中点,
所以false.
因为四边形ABCD为正方形,所以.
因为false平面false,false平面false,且false,
所以false平面false.
因为false平面false,所以false.
(2)解:连接false.
因为四边形ABCD是边长为1的正方形,
所以false.
因为false,且false,所以false.
由(1)可知false,所以false,
所以false,则false,且false.
因为false平面false,false平面false,且false,
所以false平面false.
设点false到平面false的距离为false.
因为false,所以false,
解得false.
因为false平面false,所以点E到平面false的距离为false.
假设存在满足条件的点E,则false,即false.
过E作EF⊥false,垂足为F,连接false,
则点F在false的延长线上,false.
设false,则false,
从而false,解得false.
因为点E在棱false 上,所以false,所以假设不成立,
即不存在点E,使得false与平面false所成角的正弦值为false.
同课章节目录
