2020-2021学年人教版七年级数学下册10.3数据的收集、整理与描述 单元复习(1)-2020-2021学年人教版七年级数学下册专题复习提升训练(机构)(含答案)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册10.3数据的收集、整理与描述 单元复习(1)-2020-2021学年人教版七年级数学下册专题复习提升训练(机构)(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 766.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 00:00:00 | ||
图片预览



文档简介
专题复习提升训练卷10.3《数据的收集、整理与描述》单元训练(1)
-20-21人教版七年级数学下册
一、选择题
1、以下调查中,最适合采用全面调查的是( )
A.调查某城市居民2月份人均网上购物的次数 B.调查全国中学生的平均身高
C.检测即将发射的一颗气象卫星的零部件质量 D.检测某城市的空气质量
2、为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的
是?( )
A. 随机抽取该校一个班级的学生
B. 随机抽取该校一个年级的学生
C. 随机抽取该校一部分男生
D. 分别从该校初一、初二、初三年级中各随机抽取的学生
3、下列调查最适合用抽样调查的是( )
A.审核书稿中的错别字
B.调查中学生网课期间的睡眠情况
C.调查某校的卫生死角
D.调查七(1)班同学的身高情况
4、某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有10件不合格,那么你估计该厂这20万件产品中合格品约为( )
A.2万件 B.16万件 C.18万件 D.10万件
5、记录一个人的体温变化情况,最好选用( )
A.扇形统计图 B.条形统计图 C.折线统计图 D.统计表
6、将七年级一班分成五个组,各组人数在频数分布直方图中的小长方形高的比依次为 1:2:5:3:1,人数最多的一组有25人,则该班共有 ?人.
7、某套餐营养成份的扇形统计图如图所示,已知一份套餐中蛋白质含量为70克,那么碳水化合物的含量为( )
某套餐营养成分的扇形统计图
A.35克 B.70克 C.105克 D.140克
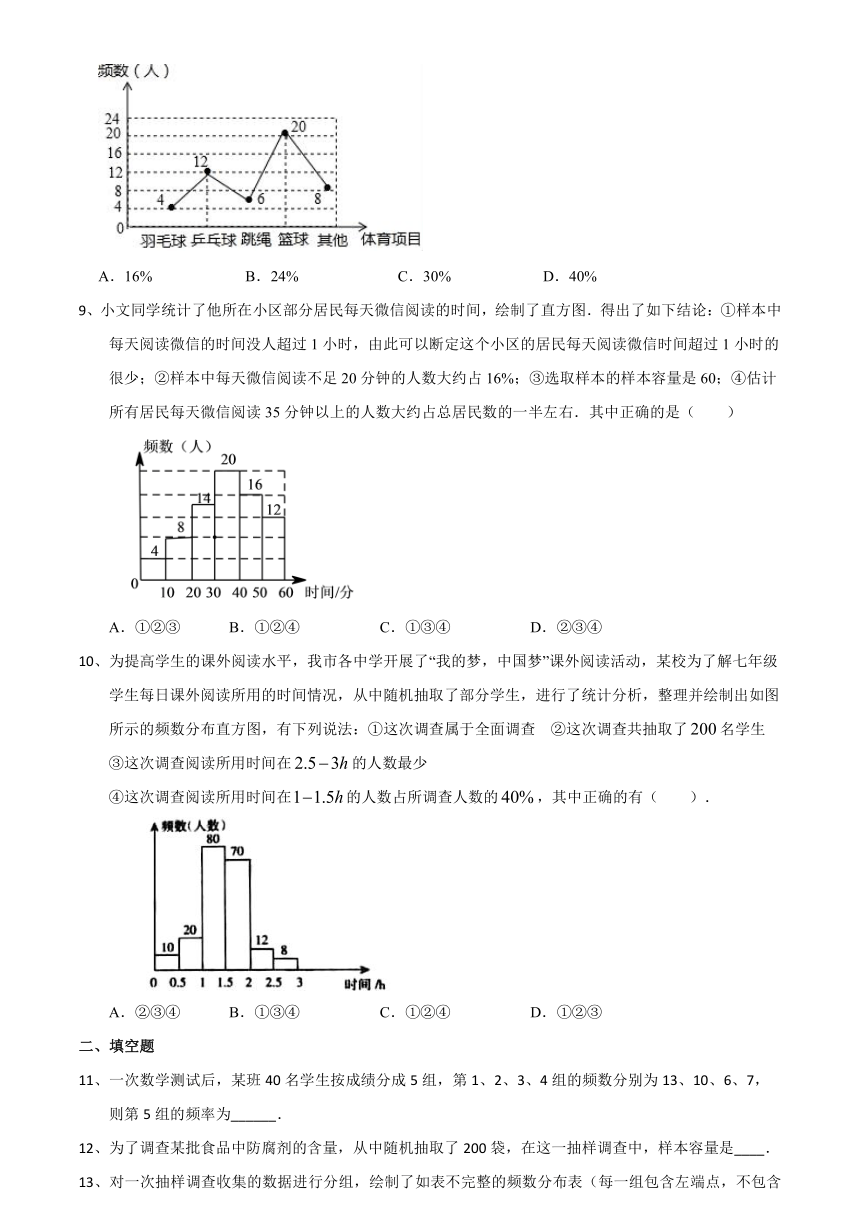
8、体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )
A.16% B.24% C.30% D.40%
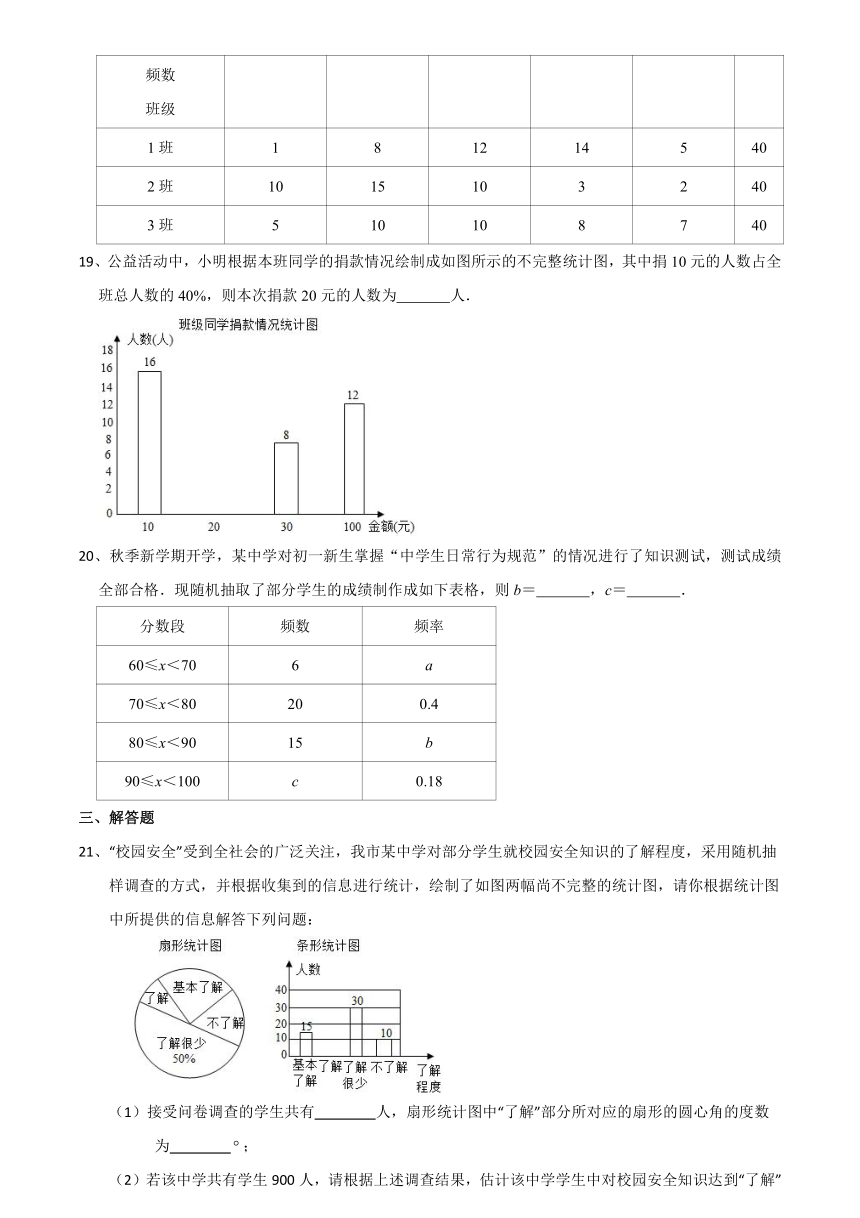
9、小文同学统计了他所在小区部分居民每天微信阅读的时间,绘制了直方图.得出了如下结论:①样本中每天阅读微信的时间没人超过1小时,由此可以断定这个小区的居民每天阅读微信时间超过1小时的很少;②样本中每天微信阅读不足20分钟的人数大约占16%;③选取样本的样本容量是60;④估计所有居民每天微信阅读35分钟以上的人数大约占总居民数的一半左右.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
10、为提高学生的课外阅读水平,我市各中学开展了“我的梦,中国梦”课外阅读活动,某校为了解七年级学生每日课外阅读所用的时间情况,从中随机抽取了部分学生,进行了统计分析,整理并绘制出如图所示的频数分布直方图,有下列说法:①这次调查属于全面调查 ②这次调查共抽取了名学生
③这次调查阅读所用时间在的人数最少
④这次调查阅读所用时间在的人数占所调查人数的,其中正确的有( ).
A.②③④ B.①③④ C.①②④ D.①②③
二、填空题
11、一次数学测试后,某班40名学生按成绩分成5组,第1、2、3、4组的频数分别为13、10、6、7,
则第5组的频率为______.
12、为了调查某批食品中防腐剂的含量,从中随机抽取了200袋,在这一抽样调查中,样本容量是____.
13、对一次抽样调查收集的数据进行分组,绘制了如表不完整的频数分布表(每一组包含左端点,不包含右端点):
分组 49.5~59.5 59.5~69.5 69.5~79.5 78.5~89.5 89.5~99.5
频数 9 15
16 12
已知第三小组(69.5~79.5)出现的频数是最后一组(89.5~99.5)频数的2倍,则这次调查抽取的样本容量是 .
14、一个有80个数据的样本中,样本中的最大值是100,最小值是40,取组距为10,
那么这些数据要分成__ 组.
15、在某校对若干名青少年进行最喜爱的运动项目的抽样调查中,得到如下统计图.如果最喜爱足球的人数比最喜爱骑自行车的人数多30人,那么参加这次调查的总人数是 人.
16、如图,直方图从左至右各长方形的高的比为2:3:4:6:1,第二组的频数为9,作品总件数为____件.
17、某中学为了了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是 .
18、小宇调查了初一年级三个班学生的身高,并进行了统计,列出如频数分布表:若要从每个班级中选取10名身高在160cm和170cm之间同学参加学校的广播操展示,不考虑其他因素的影响,则 (填“1班”,“2班”或“3班”)的可供挑选的空间最大.
身高/厘米 频数
班级 150≤x<155 155≤x<160 160≤x<165 165≤x<170 170≤x<175 合计
1班 1 8 12 14 5 40
2班 10 15 10 3 2 40
3班 5 10 10 8 7 40
19、公益活动中,小明根据本班同学的捐款情况绘制成如图所示的不完整统计图,其中捐10元的人数占全班总人数的40%,则本次捐款20元的人数为 人.
20、秋季新学期开学,某中学对初一新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格.现随机抽取了部分学生的成绩制作成如下表格,则b= ,c= .
分数段 频数 频率
60≤x<70 6 a
70≤x<80 20 0.4
80≤x<90 15 b
90≤x<100 c 0.18
三、解答题
21、“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应的扇形的圆心角的度数
为 ;
(2)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为多少人?
22、已知一个样本,27,23,25,27,29,31,27,30,32,31,28,26,27,29,28,24,26,27,28,30,以2为组距画出频数分布直方图.
23、2020年3月25日是全国中小学生安全教育日,常德芷兰实验学校为加强学生的安全意识,组织了全校8000名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.
频率分布表
分数段 频数 频率
50.5~60.5 16 0.08
60.5~70.5 40 0.2
70.5~80.5 50 0.25
80.5~90.5 m 0.35
90.5~100.5 24 n
(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图.
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
24、为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均每天唾眠时间,设每名学生的平均每天睡眠时间为x时,共分为四组:A.6≤x<7,B.7≤x<8,C.8≤x<9,D.9≤x≤10,将调查结果绘制成如图两幅不完整的统计图:
注:学生的平均每天睡眠时间不低于6时且不高于10时.
(1)本次共调查了 名学生:
(2)请补全频数分布直方图;
(3)求扇形统计图中C组所对应的圆心角度数;
(4)若该校有1500名学生,根据抽样调查结果,请估计该校学生平均每天睡眠时间不足8小时的人数.
25、某地区共有1800名九年级学生,为了解这些学生的体质健康状况,开学初随机选取部分学生进行体质健康测试,以下是根据测试成绩绘制的部分统计图表:
等级 测试成绩(分) 频数
优秀 45≤x≤50 140
良好 37.5≤x<45 36
及格 30≤x<37.5
不及格 x<30 6
根据以上信息,解答下列问题:
(1)求参加本次测试的学生数,并将频数分布表补充完整;
(2)求体质健康成绩属于“不及格”等级的频率;
(3)试估计该地区九年级学生开学初体质健康状况达到“良好”及以上等级的学生数.
26、校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食.为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有__________人,并补全条形统计图;
(2)扇形统计图中圆心角____________度;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
专题复习提升训练卷10.3《数据的收集、整理与描述》单元训练(1)
-20-21人教版七年级数学下册(解析)
一、选择题
1、以下调查中,最适合采用全面调查的是( )
A.调查某城市居民2月份人均网上购物的次数 B.调查全国中学生的平均身高
C.检测即将发射的一颗气象卫星的零部件质量 D.检测某城市的空气质量
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
【详解】解:A、调查某城市居民2月份人均网上购物的次数,适合抽样调查,故本选项不合题意;
B、调查全国中学生的平均身高,适合抽样调查,故本选项不合题意;
C、检测即将发射的一颗气象卫星的零部件质量,适合普查,故本选项符合题意;
D、检测某城市的空气质量,适合抽样调查,故本选项不合题意.
故选:C.
2、为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的
是?( )
A. 随机抽取该校一个班级的学生
B. 随机抽取该校一个年级的学生
C. 随机抽取该校一部分男生
D. 分别从该校初一、初二、初三年级中各随机抽取的学生
【答案】D
【解析】本题难度较小,考查如何进行抽查.根据抽查的特点,对照每个选项的具体内容可得,答案选择这是因为分别从该校初一、初二、初三年级中各班随机抽取的学生,能够确保每位学生都有被抽到的可能,从而保证了抽查的全面性和随机性.
3、下列调查最适合用抽样调查的是( )
A.审核书稿中的错别字
B.调查中学生网课期间的睡眠情况
C.调查某校的卫生死角
D.调查七(1)班同学的身高情况
【答案】B
【分析】在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
【详解】解:A.审核书稿中的错别字适合全面调查;
B.调查中学生网课期间的睡眠情况适合抽样调查;
C.调查某校的卫生死角适合全面调查;
D.调查七(1)班同学的身高情况适合全面调查.
故选:B.
4、某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有10件不合格,那么你估计该厂这20万件产品中合格品约为( )
A.2万件 B.16万件 C.18万件 D.10万件
【分析】先计算出100件样本中合格品的百分比,约等于这20万件的合格率,再估计该厂这20万件产品中合格品即可.
【详解】解:该厂这20万件产品中合格品约为(万件),
故选:C.
5、记录一个人的体温变化情况,最好选用( )
A.扇形统计图 B.条形统计图 C.折线统计图 D.统计表
【答案】C
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.
【详解】解:记录一个人的体温变化情况,最好用折线统计图,
故选:C.
6、将七年级一班分成五个组,各组人数在频数分布直方图中的小长方形高的比依次为 1:2:5:3:1,人数最多的一组有25人,则该班共有 ?人.
【解析】 各组人数在频数分布直方图中的小长方形高的比依次为 ,人数最多的一组有 人,
各组人数分别为 人、 人、 人、 人、 人,
总人数为:(人).
7、某套餐营养成份的扇形统计图如图所示,已知一份套餐中蛋白质含量为70克,那么碳水化合物的含量为( )
某套餐营养成分的扇形统计图
A.35克 B.70克 C.105克 D.140克
【分析】根据扇形统计图中的数据,可知蛋白质占20%,所以用70÷20%可以求得营养成分的总质量,然后再乘40%即可得到碳水化合物含量.
【详解】解:70÷20%×40%=70÷0.2×0.4=140(克),
即碳水化合物含量为140克,
故选:D.
8、体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )
A.16% B.24% C.30% D.40%
【解答】解:读图可知:
共有(4+12+6+20+8)=50人,
其中最喜欢篮球的有20人,
故频率最喜欢篮球的频率=20÷50=0.4.
故选:D.
9、小文同学统计了他所在小区部分居民每天微信阅读的时间,绘制了直方图.得出了如下结论:①样本中每天阅读微信的时间没人超过1小时,由此可以断定这个小区的居民每天阅读微信时间超过1小时的很少;②样本中每天微信阅读不足20分钟的人数大约占16%;③选取样本的样本容量是60;④估计所有居民每天微信阅读35分钟以上的人数大约占总居民数的一半左右.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
【答案】B
【分析】根据题意和频数分布直方图中的数据,可以判断各个小题中的说法是否正确,本题得以解决.
【详解】解:由直方图可得,
样本中每天阅读微信的时间没人超过1小时,由此可以断定这个小区的居民每天阅读微信时间超过1小时的很少,故①正确;
样本中每天微信阅读不足20分钟的人数大约占:(4+8)÷(4+8+14+20+16+12)×100%≈16%,故②正确;
选取样本的样本容量是:4+8+14+20+16+12=74,故③错误;
(10+16+12)÷74≈0.51,
即所有居民每天微信阅读35分钟以上的人数大约占总居民数的一半左右,故④正确:
故选:B.
10、为提高学生的课外阅读水平,我市各中学开展了“我的梦,中国梦”课外阅读活动,某校为了解七年级学生每日课外阅读所用的时间情况,从中随机抽取了部分学生,进行了统计分析,整理并绘制出如图所示的频数分布直方图,有下列说法:①这次调查属于全面调查 ②这次调查共抽取了名学生
③这次调查阅读所用时间在的人数最少
④这次调查阅读所用时间在的人数占所调查人数的,其中正确的有( ).
A.②③④ B.①③④ C.①②④ D.①②③
【答案】A
【分析】根据抽样调查和频数分布直方图的性质逐个分析计算,即可得到答案.
【详解】这次调查属于抽样调查,故①错误;
结合频数分布直方图,可计算得共抽取名学生,故②正确;
结合频数分布直方图,阅读所用时间在的共8名学生,人数最少,故③正确;
这次调查阅读所用时间在的人数占比为,即,故④正确;
故选:A.
二、填空题
11、一次数学测试后,某班40名学生按成绩分成5组,第1、2、3、4组的频数分别为13、10、6、7,
则第5组的频率为______.
【分析】根据第1-4组的频数,求出第5组的频数,即可确定出其频率.
【详解】解:第5组的频数为:,
第5组的频率为:,
故答案为:0.1.
12、为了调查某批食品中防腐剂的含量,从中随机抽取了200袋,在这一抽样调查中,样本容量是____.
【分析】根据样本容量的定义求解
【详解】∵从中随机抽取了200袋,个体的个数是200,∴样本容量是200,
故答案为:200.
13、对一次抽样调查收集的数据进行分组,绘制了如表不完整的频数分布表(每一组包含左端点,不包含右端点):
分组 49.5~59.5 59.5~69.5 69.5~79.5 78.5~89.5 89.5~99.5
频数 9 15
16 12
已知第三小组(69.5~79.5)出现的频数是最后一组(89.5~99.5)频数的2倍,则这次调查抽取的样本容量是 .
【解答】解:∵第三小组(69.5~79.5)出现的频数是最后一组(89.5~99.5)频数的2倍,且最后一组的频数为12,
∴第三组的频数为24,
则这次调查抽取的样本容量是9+15+24+16+12=76,
故答案为:76.
14、一个有80个数据的样本中,样本中的最大值是100,最小值是40,取组距为10,
那么这些数据要分成__ 组.
【分析】根据题意和题目中的数据,可以计算出要分成几组.
【详解】解:100﹣40=60,
60÷10=6,
即这些数据要分成6组,
故答案为:6.
15、在某校对若干名青少年进行最喜爱的运动项目的抽样调查中,得到如下统计图.如果最喜爱足球的人数比最喜爱骑自行车的人数多30人,那么参加这次调查的总人数是 人.
【解答】解:根据题意,可得30÷(﹣)=360(人),
即参加这次调查的总人数是360人.
故答案为:360.
16、如图,直方图从左至右各长方形的高的比为2:3:4:6:1,第二组的频数为9,作品总件数为____件.
【分析】由各长方形的高的比得到各段的频率之比,即可得到第二组的频率,再由数据总和=某段的频数÷该段的频率,即可计算作品总数.
【详解】∵从左至右各长方形的高的比为2:3:4:6:1,
∴频率之比为2:3:4:6:1;∴第二组的频率,
∵第二组的频数为9,∴作品有948(件).
故答案为:48.
17、某中学为了了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是 .
【解答】解:3000×[10(0.002+0.006+0.012)]=600,
答:这3000名学生在该次数学考试中成绩小于60分的学生数是600人.
故答案为:600人.
18、小宇调查了初一年级三个班学生的身高,并进行了统计,列出如频数分布表:若要从每个班级中选取10名身高在160cm和170cm之间同学参加学校的广播操展示,不考虑其他因素的影响,则 (填“1班”,“2班”或“3班”)的可供挑选的空间最大.
身高/厘米 频数
班级 150≤x<155 155≤x<160 160≤x<165 165≤x<170 170≤x<175 合计
1班 1 8 12 14 5 40
2班 10 15 10 3 2 40
3班 5 10 10 8 7 40
【解答】解:身高在160cm和170cm之间同学人数:一班26人,二班13人,三班18人,
因此可挑选空间最大的是一班,
故答案为:1班.
19、公益活动中,小明根据本班同学的捐款情况绘制成如图所示的不完整统计图,其中捐10元的人数占全班总人数的40%,则本次捐款20元的人数为 人.
【解答】解:∵捐10元的有16人,占全班总人数的40%,
∴全班的总人数为16÷40%=40(人),
则捐款20元的人数为40﹣(16+8+12)=4(人),
故答案为:4.
20、秋季新学期开学,某中学对初一新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格.现随机抽取了部分学生的成绩制作成如下表格,则b= ,c= .
分数段 频数 频率
60≤x<70 6 a
70≤x<80 20 0.4
80≤x<90 15 b
90≤x<100 c 0.18
【解答】解:抽取的学生总数是:20÷0.4=50(人),
b==0.3;c=50×0.18=9;
故答案为:0.3,9.
三、解答题
21、“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应的扇形的圆心角的度数
为 ;
(2)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为多少人?
【答案】(1)60,30;(2)300人
【分析】(1)从两个统计图中可知“了解很少”的频数为30人,占调查人数的50%,可求出调查人数,进而求出“了解”的频数、所占得百分比,相应的圆心角的度数;
(2)求出“了解”“基本了解”所占得百分比即可求出答案.
【详解】解:(1)接受问卷调查的人数为:(人),
“了解”的人数为:(人),
所以扇形统计图中“了解”部分所对应的扇形的圆心角的度数为:,
故答案为:60,30;
(2)“了解”和“基本了解”的人数为(人),
因此整体中,达到“了解”和“基本了解”的人数为:(人),
答:该中学900中对校园安全知识达到“了解”和“基本了解”的共有300人.
22、已知一个样本,27,23,25,27,29,31,27,30,32,31,28,26,27,29,28,24,26,27,28,30,以2为组距画出频数分布直方图.
解:(1)计算最大值与最小值的差:32-23=9.
(2)确定组数与组距:已知组距为2,则9÷2=4.5,因此定为5组.
(3)决定分点,所分的五个小组是:
22.5~24.5,24.5~26.5,26.5~28.5,28.5~30.5,30.5~32.5.
(4)列频数分布表:
(5)画频数分布直方图:
23、2020年3月25日是全国中小学生安全教育日,常德芷兰实验学校为加强学生的安全意识,组织了全校8000名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.
频率分布表
分数段 频数 频率
50.5~60.5 16 0.08
60.5~70.5 40 0.2
70.5~80.5 50 0.25
80.5~90.5 m 0.35
90.5~100.5 24 n
(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图.
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
【解答】解:(1)16÷0.08=200,
m=200×0.35=70,n=24÷200=0.12;
故答案为200,70;0.12;
(2)如图,
(3)8000×(0.08+0.2)=2240,
所以该校安全意识不强的学生约有2240人.
24、为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均每天唾眠时间,设每名学生的平均每天睡眠时间为x时,共分为四组:A.6≤x<7,B.7≤x<8,C.8≤x<9,D.9≤x≤10,将调查结果绘制成如图两幅不完整的统计图:
注:学生的平均每天睡眠时间不低于6时且不高于10时.
(1)本次共调查了 名学生:
(2)请补全频数分布直方图;
(3)求扇形统计图中C组所对应的圆心角度数;
(4)若该校有1500名学生,根据抽样调查结果,请估计该校学生平均每天睡眠时间不足8小时的人数.
【答案】(1)50;(2)补全的频数分布直方图见解析;(3)扇形统计图中C组所对应的圆心角度数为72°;(4)估计该校学生平均每天睡眠时间不足8小时的有690人.
【分析】(1)根据D组的人数和所占的百分比,可以计算出本次共调查了多少名学生;
(2)根据(1)中的结果和频数分布直方图中的数据,可以计算出C组的人数,然后即可将频数分布直方图补充完整;
(3)根据频数分布直方图中的数据,可以计算出扇形统计图中C组所对应的圆心角度数;
(4)根据直方图中的数据,可以计算出该校学生平均每天睡眠时间不足8小时的人数.
【详解】解:(1)本次共调查了17÷34%=50名学生,
故答案为:50;
(2)C组学生有:50﹣5﹣18﹣17=10(人),
补全的频数分布直方图如下图所示
(3)360°×=72°,即扇形统计图中C组所对应的圆心角度数为72°;
(4)1500×=690(人),即估计该校学生平均每天睡眠时间不足8小时的有690人.
25、某地区共有1800名九年级学生,为了解这些学生的体质健康状况,开学初随机选取部分学生进行体质健康测试,以下是根据测试成绩绘制的部分统计图表:
等级 测试成绩(分) 频数
优秀 45≤x≤50 140
良好 37.5≤x<45 36
及格 30≤x<37.5
不及格 x<30 6
根据以上信息,解答下列问题:
(1)求参加本次测试的学生数,并将频数分布表补充完整;
(2)求体质健康成绩属于“不及格”等级的频率;
(3)试估计该地区九年级学生开学初体质健康状况达到“良好”及以上等级的学生数.
【解答】解:(1)140÷0.7=200(人)
答:参加本次测试的学生数为200人,
200﹣140﹣36﹣6=18(人),
故答案为:18;
(2)6÷200=0.03,
答:体质健康成绩属于“不及格”等级的频率为0.03;
(3)1800×=1584(人),
答:达到“良好”及以上等级的学生数为1584人.
26、校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食.为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有__________人,并补全条形统计图;
(2)扇形统计图中圆心角____________度;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
【答案】(1)1000,图见解析;(2)72;(3)900.
【分析】(1)根据不剩的学生数和所占的百分比可以求得这次被调查的同学数;再求得剩少量的学生数,从而可以将条形统计图补充完整;
(2)根据统计图中的数据可以求得扇形统计图中圆心角的度数;
(3)根据题被调查的同学总数占该校18000名学生的分数即可估算出结果.
【详解】解:(1)(人,即这次被调查的同学共有1000人,
故答案为:1000;
剩少量的学生有:(人,
补全的条形统计图如图所示;
(3)扇形统计图中圆心角,故答案为:72;
(4)(人,
答:该校18000名学生一餐浪费的食物可供900人食用一餐.
-20-21人教版七年级数学下册
一、选择题
1、以下调查中,最适合采用全面调查的是( )
A.调查某城市居民2月份人均网上购物的次数 B.调查全国中学生的平均身高
C.检测即将发射的一颗气象卫星的零部件质量 D.检测某城市的空气质量
2、为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的
是?( )
A. 随机抽取该校一个班级的学生
B. 随机抽取该校一个年级的学生
C. 随机抽取该校一部分男生
D. 分别从该校初一、初二、初三年级中各随机抽取的学生
3、下列调查最适合用抽样调查的是( )
A.审核书稿中的错别字
B.调查中学生网课期间的睡眠情况
C.调查某校的卫生死角
D.调查七(1)班同学的身高情况
4、某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有10件不合格,那么你估计该厂这20万件产品中合格品约为( )
A.2万件 B.16万件 C.18万件 D.10万件
5、记录一个人的体温变化情况,最好选用( )
A.扇形统计图 B.条形统计图 C.折线统计图 D.统计表
6、将七年级一班分成五个组,各组人数在频数分布直方图中的小长方形高的比依次为 1:2:5:3:1,人数最多的一组有25人,则该班共有 ?人.
7、某套餐营养成份的扇形统计图如图所示,已知一份套餐中蛋白质含量为70克,那么碳水化合物的含量为( )
某套餐营养成分的扇形统计图
A.35克 B.70克 C.105克 D.140克
8、体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )
A.16% B.24% C.30% D.40%
9、小文同学统计了他所在小区部分居民每天微信阅读的时间,绘制了直方图.得出了如下结论:①样本中每天阅读微信的时间没人超过1小时,由此可以断定这个小区的居民每天阅读微信时间超过1小时的很少;②样本中每天微信阅读不足20分钟的人数大约占16%;③选取样本的样本容量是60;④估计所有居民每天微信阅读35分钟以上的人数大约占总居民数的一半左右.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
10、为提高学生的课外阅读水平,我市各中学开展了“我的梦,中国梦”课外阅读活动,某校为了解七年级学生每日课外阅读所用的时间情况,从中随机抽取了部分学生,进行了统计分析,整理并绘制出如图所示的频数分布直方图,有下列说法:①这次调查属于全面调查 ②这次调查共抽取了名学生
③这次调查阅读所用时间在的人数最少
④这次调查阅读所用时间在的人数占所调查人数的,其中正确的有( ).
A.②③④ B.①③④ C.①②④ D.①②③
二、填空题
11、一次数学测试后,某班40名学生按成绩分成5组,第1、2、3、4组的频数分别为13、10、6、7,
则第5组的频率为______.
12、为了调查某批食品中防腐剂的含量,从中随机抽取了200袋,在这一抽样调查中,样本容量是____.
13、对一次抽样调查收集的数据进行分组,绘制了如表不完整的频数分布表(每一组包含左端点,不包含右端点):
分组 49.5~59.5 59.5~69.5 69.5~79.5 78.5~89.5 89.5~99.5
频数 9 15
16 12
已知第三小组(69.5~79.5)出现的频数是最后一组(89.5~99.5)频数的2倍,则这次调查抽取的样本容量是 .
14、一个有80个数据的样本中,样本中的最大值是100,最小值是40,取组距为10,
那么这些数据要分成__ 组.
15、在某校对若干名青少年进行最喜爱的运动项目的抽样调查中,得到如下统计图.如果最喜爱足球的人数比最喜爱骑自行车的人数多30人,那么参加这次调查的总人数是 人.
16、如图,直方图从左至右各长方形的高的比为2:3:4:6:1,第二组的频数为9,作品总件数为____件.
17、某中学为了了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是 .
18、小宇调查了初一年级三个班学生的身高,并进行了统计,列出如频数分布表:若要从每个班级中选取10名身高在160cm和170cm之间同学参加学校的广播操展示,不考虑其他因素的影响,则 (填“1班”,“2班”或“3班”)的可供挑选的空间最大.
身高/厘米 频数
班级 150≤x<155 155≤x<160 160≤x<165 165≤x<170 170≤x<175 合计
1班 1 8 12 14 5 40
2班 10 15 10 3 2 40
3班 5 10 10 8 7 40
19、公益活动中,小明根据本班同学的捐款情况绘制成如图所示的不完整统计图,其中捐10元的人数占全班总人数的40%,则本次捐款20元的人数为 人.
20、秋季新学期开学,某中学对初一新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格.现随机抽取了部分学生的成绩制作成如下表格,则b= ,c= .
分数段 频数 频率
60≤x<70 6 a
70≤x<80 20 0.4
80≤x<90 15 b
90≤x<100 c 0.18
三、解答题
21、“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应的扇形的圆心角的度数
为 ;
(2)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为多少人?
22、已知一个样本,27,23,25,27,29,31,27,30,32,31,28,26,27,29,28,24,26,27,28,30,以2为组距画出频数分布直方图.
23、2020年3月25日是全国中小学生安全教育日,常德芷兰实验学校为加强学生的安全意识,组织了全校8000名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.
频率分布表
分数段 频数 频率
50.5~60.5 16 0.08
60.5~70.5 40 0.2
70.5~80.5 50 0.25
80.5~90.5 m 0.35
90.5~100.5 24 n
(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图.
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
24、为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均每天唾眠时间,设每名学生的平均每天睡眠时间为x时,共分为四组:A.6≤x<7,B.7≤x<8,C.8≤x<9,D.9≤x≤10,将调查结果绘制成如图两幅不完整的统计图:
注:学生的平均每天睡眠时间不低于6时且不高于10时.
(1)本次共调查了 名学生:
(2)请补全频数分布直方图;
(3)求扇形统计图中C组所对应的圆心角度数;
(4)若该校有1500名学生,根据抽样调查结果,请估计该校学生平均每天睡眠时间不足8小时的人数.
25、某地区共有1800名九年级学生,为了解这些学生的体质健康状况,开学初随机选取部分学生进行体质健康测试,以下是根据测试成绩绘制的部分统计图表:
等级 测试成绩(分) 频数
优秀 45≤x≤50 140
良好 37.5≤x<45 36
及格 30≤x<37.5
不及格 x<30 6
根据以上信息,解答下列问题:
(1)求参加本次测试的学生数,并将频数分布表补充完整;
(2)求体质健康成绩属于“不及格”等级的频率;
(3)试估计该地区九年级学生开学初体质健康状况达到“良好”及以上等级的学生数.
26、校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食.为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有__________人,并补全条形统计图;
(2)扇形统计图中圆心角____________度;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
专题复习提升训练卷10.3《数据的收集、整理与描述》单元训练(1)
-20-21人教版七年级数学下册(解析)
一、选择题
1、以下调查中,最适合采用全面调查的是( )
A.调查某城市居民2月份人均网上购物的次数 B.调查全国中学生的平均身高
C.检测即将发射的一颗气象卫星的零部件质量 D.检测某城市的空气质量
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
【详解】解:A、调查某城市居民2月份人均网上购物的次数,适合抽样调查,故本选项不合题意;
B、调查全国中学生的平均身高,适合抽样调查,故本选项不合题意;
C、检测即将发射的一颗气象卫星的零部件质量,适合普查,故本选项符合题意;
D、检测某城市的空气质量,适合抽样调查,故本选项不合题意.
故选:C.
2、为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的
是?( )
A. 随机抽取该校一个班级的学生
B. 随机抽取该校一个年级的学生
C. 随机抽取该校一部分男生
D. 分别从该校初一、初二、初三年级中各随机抽取的学生
【答案】D
【解析】本题难度较小,考查如何进行抽查.根据抽查的特点,对照每个选项的具体内容可得,答案选择这是因为分别从该校初一、初二、初三年级中各班随机抽取的学生,能够确保每位学生都有被抽到的可能,从而保证了抽查的全面性和随机性.
3、下列调查最适合用抽样调查的是( )
A.审核书稿中的错别字
B.调查中学生网课期间的睡眠情况
C.调查某校的卫生死角
D.调查七(1)班同学的身高情况
【答案】B
【分析】在要求精确、难度相对不大,实验无破坏性的情况下应选择普查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,普查就受到限制,这时就应选择抽样调查.
【详解】解:A.审核书稿中的错别字适合全面调查;
B.调查中学生网课期间的睡眠情况适合抽样调查;
C.调查某校的卫生死角适合全面调查;
D.调查七(1)班同学的身高情况适合全面调查.
故选:B.
4、某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有10件不合格,那么你估计该厂这20万件产品中合格品约为( )
A.2万件 B.16万件 C.18万件 D.10万件
【分析】先计算出100件样本中合格品的百分比,约等于这20万件的合格率,再估计该厂这20万件产品中合格品即可.
【详解】解:该厂这20万件产品中合格品约为(万件),
故选:C.
5、记录一个人的体温变化情况,最好选用( )
A.扇形统计图 B.条形统计图 C.折线统计图 D.统计表
【答案】C
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.
【详解】解:记录一个人的体温变化情况,最好用折线统计图,
故选:C.
6、将七年级一班分成五个组,各组人数在频数分布直方图中的小长方形高的比依次为 1:2:5:3:1,人数最多的一组有25人,则该班共有 ?人.
【解析】 各组人数在频数分布直方图中的小长方形高的比依次为 ,人数最多的一组有 人,
各组人数分别为 人、 人、 人、 人、 人,
总人数为:(人).
7、某套餐营养成份的扇形统计图如图所示,已知一份套餐中蛋白质含量为70克,那么碳水化合物的含量为( )
某套餐营养成分的扇形统计图
A.35克 B.70克 C.105克 D.140克
【分析】根据扇形统计图中的数据,可知蛋白质占20%,所以用70÷20%可以求得营养成分的总质量,然后再乘40%即可得到碳水化合物含量.
【详解】解:70÷20%×40%=70÷0.2×0.4=140(克),
即碳水化合物含量为140克,
故选:D.
8、体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )
A.16% B.24% C.30% D.40%
【解答】解:读图可知:
共有(4+12+6+20+8)=50人,
其中最喜欢篮球的有20人,
故频率最喜欢篮球的频率=20÷50=0.4.
故选:D.
9、小文同学统计了他所在小区部分居民每天微信阅读的时间,绘制了直方图.得出了如下结论:①样本中每天阅读微信的时间没人超过1小时,由此可以断定这个小区的居民每天阅读微信时间超过1小时的很少;②样本中每天微信阅读不足20分钟的人数大约占16%;③选取样本的样本容量是60;④估计所有居民每天微信阅读35分钟以上的人数大约占总居民数的一半左右.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
【答案】B
【分析】根据题意和频数分布直方图中的数据,可以判断各个小题中的说法是否正确,本题得以解决.
【详解】解:由直方图可得,
样本中每天阅读微信的时间没人超过1小时,由此可以断定这个小区的居民每天阅读微信时间超过1小时的很少,故①正确;
样本中每天微信阅读不足20分钟的人数大约占:(4+8)÷(4+8+14+20+16+12)×100%≈16%,故②正确;
选取样本的样本容量是:4+8+14+20+16+12=74,故③错误;
(10+16+12)÷74≈0.51,
即所有居民每天微信阅读35分钟以上的人数大约占总居民数的一半左右,故④正确:
故选:B.
10、为提高学生的课外阅读水平,我市各中学开展了“我的梦,中国梦”课外阅读活动,某校为了解七年级学生每日课外阅读所用的时间情况,从中随机抽取了部分学生,进行了统计分析,整理并绘制出如图所示的频数分布直方图,有下列说法:①这次调查属于全面调查 ②这次调查共抽取了名学生
③这次调查阅读所用时间在的人数最少
④这次调查阅读所用时间在的人数占所调查人数的,其中正确的有( ).
A.②③④ B.①③④ C.①②④ D.①②③
【答案】A
【分析】根据抽样调查和频数分布直方图的性质逐个分析计算,即可得到答案.
【详解】这次调查属于抽样调查,故①错误;
结合频数分布直方图,可计算得共抽取名学生,故②正确;
结合频数分布直方图,阅读所用时间在的共8名学生,人数最少,故③正确;
这次调查阅读所用时间在的人数占比为,即,故④正确;
故选:A.
二、填空题
11、一次数学测试后,某班40名学生按成绩分成5组,第1、2、3、4组的频数分别为13、10、6、7,
则第5组的频率为______.
【分析】根据第1-4组的频数,求出第5组的频数,即可确定出其频率.
【详解】解:第5组的频数为:,
第5组的频率为:,
故答案为:0.1.
12、为了调查某批食品中防腐剂的含量,从中随机抽取了200袋,在这一抽样调查中,样本容量是____.
【分析】根据样本容量的定义求解
【详解】∵从中随机抽取了200袋,个体的个数是200,∴样本容量是200,
故答案为:200.
13、对一次抽样调查收集的数据进行分组,绘制了如表不完整的频数分布表(每一组包含左端点,不包含右端点):
分组 49.5~59.5 59.5~69.5 69.5~79.5 78.5~89.5 89.5~99.5
频数 9 15
16 12
已知第三小组(69.5~79.5)出现的频数是最后一组(89.5~99.5)频数的2倍,则这次调查抽取的样本容量是 .
【解答】解:∵第三小组(69.5~79.5)出现的频数是最后一组(89.5~99.5)频数的2倍,且最后一组的频数为12,
∴第三组的频数为24,
则这次调查抽取的样本容量是9+15+24+16+12=76,
故答案为:76.
14、一个有80个数据的样本中,样本中的最大值是100,最小值是40,取组距为10,
那么这些数据要分成__ 组.
【分析】根据题意和题目中的数据,可以计算出要分成几组.
【详解】解:100﹣40=60,
60÷10=6,
即这些数据要分成6组,
故答案为:6.
15、在某校对若干名青少年进行最喜爱的运动项目的抽样调查中,得到如下统计图.如果最喜爱足球的人数比最喜爱骑自行车的人数多30人,那么参加这次调查的总人数是 人.
【解答】解:根据题意,可得30÷(﹣)=360(人),
即参加这次调查的总人数是360人.
故答案为:360.
16、如图,直方图从左至右各长方形的高的比为2:3:4:6:1,第二组的频数为9,作品总件数为____件.
【分析】由各长方形的高的比得到各段的频率之比,即可得到第二组的频率,再由数据总和=某段的频数÷该段的频率,即可计算作品总数.
【详解】∵从左至右各长方形的高的比为2:3:4:6:1,
∴频率之比为2:3:4:6:1;∴第二组的频率,
∵第二组的频数为9,∴作品有948(件).
故答案为:48.
17、某中学为了了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是 .
【解答】解:3000×[10(0.002+0.006+0.012)]=600,
答:这3000名学生在该次数学考试中成绩小于60分的学生数是600人.
故答案为:600人.
18、小宇调查了初一年级三个班学生的身高,并进行了统计,列出如频数分布表:若要从每个班级中选取10名身高在160cm和170cm之间同学参加学校的广播操展示,不考虑其他因素的影响,则 (填“1班”,“2班”或“3班”)的可供挑选的空间最大.
身高/厘米 频数
班级 150≤x<155 155≤x<160 160≤x<165 165≤x<170 170≤x<175 合计
1班 1 8 12 14 5 40
2班 10 15 10 3 2 40
3班 5 10 10 8 7 40
【解答】解:身高在160cm和170cm之间同学人数:一班26人,二班13人,三班18人,
因此可挑选空间最大的是一班,
故答案为:1班.
19、公益活动中,小明根据本班同学的捐款情况绘制成如图所示的不完整统计图,其中捐10元的人数占全班总人数的40%,则本次捐款20元的人数为 人.
【解答】解:∵捐10元的有16人,占全班总人数的40%,
∴全班的总人数为16÷40%=40(人),
则捐款20元的人数为40﹣(16+8+12)=4(人),
故答案为:4.
20、秋季新学期开学,某中学对初一新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格.现随机抽取了部分学生的成绩制作成如下表格,则b= ,c= .
分数段 频数 频率
60≤x<70 6 a
70≤x<80 20 0.4
80≤x<90 15 b
90≤x<100 c 0.18
【解答】解:抽取的学生总数是:20÷0.4=50(人),
b==0.3;c=50×0.18=9;
故答案为:0.3,9.
三、解答题
21、“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应的扇形的圆心角的度数
为 ;
(2)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为多少人?
【答案】(1)60,30;(2)300人
【分析】(1)从两个统计图中可知“了解很少”的频数为30人,占调查人数的50%,可求出调查人数,进而求出“了解”的频数、所占得百分比,相应的圆心角的度数;
(2)求出“了解”“基本了解”所占得百分比即可求出答案.
【详解】解:(1)接受问卷调查的人数为:(人),
“了解”的人数为:(人),
所以扇形统计图中“了解”部分所对应的扇形的圆心角的度数为:,
故答案为:60,30;
(2)“了解”和“基本了解”的人数为(人),
因此整体中,达到“了解”和“基本了解”的人数为:(人),
答:该中学900中对校园安全知识达到“了解”和“基本了解”的共有300人.
22、已知一个样本,27,23,25,27,29,31,27,30,32,31,28,26,27,29,28,24,26,27,28,30,以2为组距画出频数分布直方图.
解:(1)计算最大值与最小值的差:32-23=9.
(2)确定组数与组距:已知组距为2,则9÷2=4.5,因此定为5组.
(3)决定分点,所分的五个小组是:
22.5~24.5,24.5~26.5,26.5~28.5,28.5~30.5,30.5~32.5.
(4)列频数分布表:
(5)画频数分布直方图:
23、2020年3月25日是全国中小学生安全教育日,常德芷兰实验学校为加强学生的安全意识,组织了全校8000名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.
频率分布表
分数段 频数 频率
50.5~60.5 16 0.08
60.5~70.5 40 0.2
70.5~80.5 50 0.25
80.5~90.5 m 0.35
90.5~100.5 24 n
(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图.
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
【解答】解:(1)16÷0.08=200,
m=200×0.35=70,n=24÷200=0.12;
故答案为200,70;0.12;
(2)如图,
(3)8000×(0.08+0.2)=2240,
所以该校安全意识不强的学生约有2240人.
24、为了解某校学生的睡眠情况,该校数学小组随机调查了部分学生一周的平均每天唾眠时间,设每名学生的平均每天睡眠时间为x时,共分为四组:A.6≤x<7,B.7≤x<8,C.8≤x<9,D.9≤x≤10,将调查结果绘制成如图两幅不完整的统计图:
注:学生的平均每天睡眠时间不低于6时且不高于10时.
(1)本次共调查了 名学生:
(2)请补全频数分布直方图;
(3)求扇形统计图中C组所对应的圆心角度数;
(4)若该校有1500名学生,根据抽样调查结果,请估计该校学生平均每天睡眠时间不足8小时的人数.
【答案】(1)50;(2)补全的频数分布直方图见解析;(3)扇形统计图中C组所对应的圆心角度数为72°;(4)估计该校学生平均每天睡眠时间不足8小时的有690人.
【分析】(1)根据D组的人数和所占的百分比,可以计算出本次共调查了多少名学生;
(2)根据(1)中的结果和频数分布直方图中的数据,可以计算出C组的人数,然后即可将频数分布直方图补充完整;
(3)根据频数分布直方图中的数据,可以计算出扇形统计图中C组所对应的圆心角度数;
(4)根据直方图中的数据,可以计算出该校学生平均每天睡眠时间不足8小时的人数.
【详解】解:(1)本次共调查了17÷34%=50名学生,
故答案为:50;
(2)C组学生有:50﹣5﹣18﹣17=10(人),
补全的频数分布直方图如下图所示
(3)360°×=72°,即扇形统计图中C组所对应的圆心角度数为72°;
(4)1500×=690(人),即估计该校学生平均每天睡眠时间不足8小时的有690人.
25、某地区共有1800名九年级学生,为了解这些学生的体质健康状况,开学初随机选取部分学生进行体质健康测试,以下是根据测试成绩绘制的部分统计图表:
等级 测试成绩(分) 频数
优秀 45≤x≤50 140
良好 37.5≤x<45 36
及格 30≤x<37.5
不及格 x<30 6
根据以上信息,解答下列问题:
(1)求参加本次测试的学生数,并将频数分布表补充完整;
(2)求体质健康成绩属于“不及格”等级的频率;
(3)试估计该地区九年级学生开学初体质健康状况达到“良好”及以上等级的学生数.
【解答】解:(1)140÷0.7=200(人)
答:参加本次测试的学生数为200人,
200﹣140﹣36﹣6=18(人),
故答案为:18;
(2)6÷200=0.03,
答:体质健康成绩属于“不及格”等级的频率为0.03;
(3)1800×=1584(人),
答:达到“良好”及以上等级的学生数为1584人.
26、校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食.为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)这次被调查的同学共有__________人,并补全条形统计图;
(2)扇形统计图中圆心角____________度;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
【答案】(1)1000,图见解析;(2)72;(3)900.
【分析】(1)根据不剩的学生数和所占的百分比可以求得这次被调查的同学数;再求得剩少量的学生数,从而可以将条形统计图补充完整;
(2)根据统计图中的数据可以求得扇形统计图中圆心角的度数;
(3)根据题被调查的同学总数占该校18000名学生的分数即可估算出结果.
【详解】解:(1)(人,即这次被调查的同学共有1000人,
故答案为:1000;
剩少量的学生有:(人,
补全的条形统计图如图所示;
(3)扇形统计图中圆心角,故答案为:72;
(4)(人,
答:该校18000名学生一餐浪费的食物可供900人食用一餐.
