2020-2021学年人教版七年级数学下册 10.2直方图专题复习提升训练(机构)(word版含解析)
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册 10.2直方图专题复习提升训练(机构)(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 796.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 01:26:38 | ||
图片预览



文档简介
专题复习提升训练卷10.2直方图-20-21人教版七年级数学下册
一、选择题
1、将40个数据分成五组,编成组号为①~⑤的五个组,频数分布如表:
组号 ① ② ③ ④ ⑤
频数 12 4 6
10
则第4组的频率是( )
A.0.2 B.0.3 C.8 D.12
2、一组数据共60个,分为6组,第1至第4组的频数分别为6,8,9,11,第5组的频率为0.20,则第6组的频数为( )
A.11 B.13 C.14 D.15
3、在全班45人中进行了你最喜爱的电视节目的调查活动,喜爱的电视剧有人数为18人,喜爱动画片有人数为15人,喜爱体育节目有人数为10人,则下列说法正确的是( )
A.喜爱的电视剧的人数的频率是 B.喜爱的电视剧的人数的频率是
C.喜爱的动画片的人数的频率是 D.喜爱的体育节目的人数的频率是
4、某公路上的测速仪,在某一时间段内测得30辆汽车的速度(单位:km/h),其最大值和最小值分别是80,56.为了制作频数直方图,以5为组距,这样,可以把数据分成( )
A.4组 B.5组 C.6组 D.10组
5、市某视力健康管理中心对全市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数直方图,则这组数据的组数与组距分别是( )
A.4和0.20 B.4和0.30 C.5和0.20 D.5和0.30
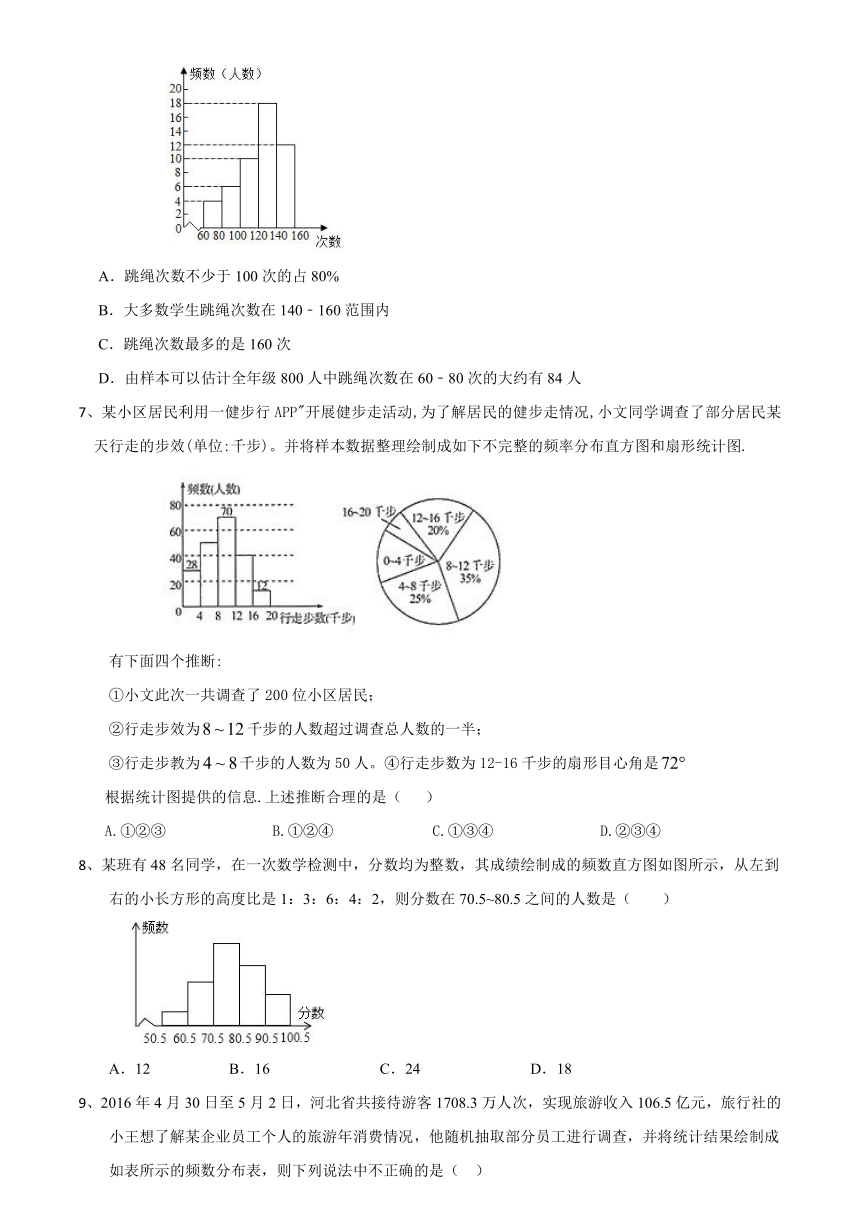
6、为了了解某校七年级800名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为:60≤x<80),则以下说法正确的是( )
A.跳绳次数不少于100次的占80%
B.大多数学生跳绳次数在140﹣160范围内
C.跳绳次数最多的是160次
D.由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有84人
7、某小区居民利用一健步行APP"开展健步走活动,为了解居民的健步走情况,小文同学调查了部分居民某天行走的步效(单位:千步)。并将样本数据整理绘制成如下不完整的频率分布直方图和扇形统计图.
有下面四个推断:
①小文此次一共调查了200位小区居民;
②行走步效为千步的人数超过调查总人数的一半;
③行走步教为千步的人数为50人。④行走步数为12-16千步的扇形目心角是
根据统计图提供的信息.上述推断合理的是( )
A.①②③ B.①②④ C.①③④ D.②③④
8、某班有48名同学,在一次数学检测中,分数均为整数,其成绩绘制成的频数直方图如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则分数在70.5~80.5之间的人数是( )
A.12 B.16 C.24 D.18
9、2016年4月30日至5月2日,河北省共接待游客1708.3万人次,实现旅游收入106.5亿元,旅行社的小王想了解某企业员工个人的旅游年消费情况,他随机抽取部分员工进行调查,并将统计结果绘制成如表所示的频数分布表,则下列说法中不正确的是( )
个人旅游年 消费金额/元
频数
A.小王随机抽取了100名员工
B.在频数分布表中,组距是2000,组数是5组
C.个人旅游年消费金额在6000元以上的人数占随机抽取人数的22%
D.在随机抽取的员工中,个人旅游年消费金额在4000元以下(包括4000元)的共有37人
10、如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )
A.该班总人数为50人 B.步行人数为30人
C.乘车人数是骑车人数的2.5倍 D.骑车人数占20%
二、填空题
11、将一个有80个数据的样本经统计分成6组,若某一组的频率为0.15,则该组的频数为 .
12、老师在黑板上随手写下一串数字“002 200 220”,则数字“0”出现的频率是_______.
13、将一批数据分成5组,列出分布表,其中第二组与第五组的频率都是0.21,第一组与第三组的频率之和是0.44,那么第四组的频率是 .
14、2020年綦江区中招体考已结束,数据显示,与去年相比,体考成绩略有下滑.今年某中学某班学生体育毕业考试的成绩(成绩取整数),制成如图所示的频数分布直方图,若成绩在44.5~47.5分范围内为良好,则该班学生体育成绩良好的百分率是 .
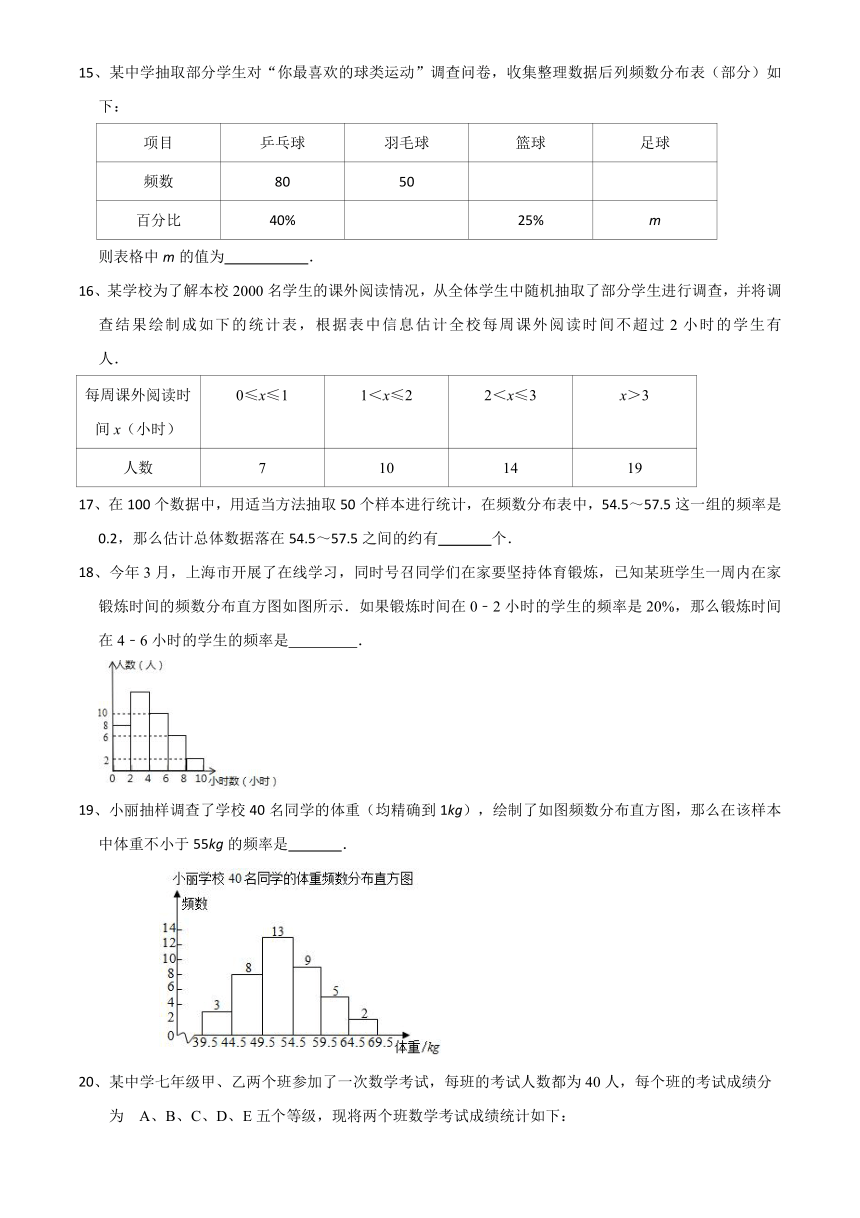
15、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷,收集整理数据后列频数分布表(部分)如下:
项目 乒乓球 羽毛球 篮球 足球
频数 80 50
百分比 40%
25% m
则表格中m的值为 .
16、某学校为了解本校2000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时) 0≤x≤1 1<x≤2 2<x≤3 x>3
人数 7 10 14 19
17、在100个数据中,用适当方法抽取50个样本进行统计,在频数分布表中,54.5~57.5这一组的频率是0.2,那么估计总体数据落在54.5~57.5之间的约有 个.
18、今年3月,上海市开展了在线学习,同时号召同学们在家要坚持体育锻炼,已知某班学生一周内在家锻炼时间的频数分布直方图如图所示.如果锻炼时间在0﹣2小时的学生的频率是20%,那么锻炼时间在4﹣6小时的学生的频率是 .
19、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
20、某中学七年级甲、乙两个班参加了一次数学考试,每班的考试人数都为40人,每个班的考试成绩分
为 A、B、C、D、E五个等级,现将两个班数学考试成绩统计如下:
根据以上统计图提供的信息,可知两个班人数相等的等级是__________.
三、解答题
21、八甲班进行了一次数学考试,将成绩绘制成了如下不完整的频数分布表和频数直方图:
(1)求频数分布表中a和b的值;
(2)将频数直方图补充完整;
(3)成绩不低于60分为及格,该班本次数学考试的及格率是多少?
成绩 频数(人数) 频率
50≤x<60 5 0.1
60≤x<70 10 0.2
70≤x<80 20 0.4
80≤x<90 a 0.2
90≤x<100 5 b
22、随着车辆的增加,交通违规的现象越来越严重.交警对某雷达测速区监测到的一组汽车的时速数据进行整理,得到其频数及频率如表
数据段 频数 频率
30~40 10 0.05
40~50 36
50~60
0.39
60~70 56
70~80 20 0.10
总计 200 1
注:30~40为时速大于30千米而小于40千米,其他类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
23、某公司共有400名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成统计图表进行分析.频数分布表
组别 销售数量(件) 频数 频率
A 20≤x<40 3 0.06
B 40≤x<60 7 0.14
C 60≤x<80 12 a
D 80≤x<100 m 0.48
E 100≤x<120 4 0.08
合计 b 1
请根据以上信息,解决下列问题:
(1)频数分布表中,a= 、b= ;
(2)补全频数分布直方图;
(3)如果该季度销量不低于100件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.
24、为庆祝中华人民共和国成立70周年,郑州市某校组织八年级学生进行“方阵表演”.为了整齐划一,需了解学生的身高,现随机抽取该校八年级学生进行抽样调查,根据所得数据绘制出如下统计图表
组别 身高
A
B
C
D
E
根据图表提供的信息,回答下列问题:
(1)这次抽样调查,一共抽取学生_________人;
(2)扇形统计图中,扇形E的圆心角度数是_________;
(3)请补全频数分布直方图;
(4)已知该校八年级共有学生400人,请估计身高在的学生约有多少人?
25、为弘扬中华传统文化,某校组织七年级名学生参加汉字听写大赛,为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为分)进行统计分析,得到如下所示的频数分布表:
分数段
频数
所占百分比
请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查的样本容量为_______,表中_______,_______;
(2)补全频数分布直方图;
(3)若成绩超过分为优秀,估计该校七年级学生中汉字听写能力为优秀的约有多少人?
专题复习提升训练卷10.2直方图-20-21人教版七年级数学下册(解析)
一、选择题
1、将40个数据分成五组,编成组号为①~⑤的五个组,频数分布如表:
组号 ① ② ③ ④ ⑤
频数 12 4 6
10
则第4组的频率是( )
A.0.2 B.0.3 C.8 D.12
解:根据频数分布表中的数据可知:
第4组的频数为:40﹣12﹣4﹣6﹣10=8,
所以第4组的频率为:8÷40=0.2.
故选:A.
2、一组数据共60个,分为6组,第1至第4组的频数分别为6,8,9,11,第5组的频率为0.20,则第6组的频数为( )
A.11 B.13 C.14 D.15
【答案】C
【分析】首先根据频数=总数×频率,求得第五组频数;再根据各组的频数和等于总数,求得第六组的频数.
【详解】解:根据题意,得
第五组频数是60×0.20=12,
故第六组的频数是60-6-8-9-11-12=14.
故选:C.
3、在全班45人中进行了你最喜爱的电视节目的调查活动,喜爱的电视剧有人数为18人,喜爱动画片有人数为15人,喜爱体育节目有人数为10人,则下列说法正确的是( )
A.喜爱的电视剧的人数的频率是 B.喜爱的电视剧的人数的频率是
C.喜爱的动画片的人数的频率是 D.喜爱的体育节目的人数的频率是
【答案】B
【解析】频率应为频数除以总数,所以喜欢看电视剧、动画片和体育节目的频率分别是、、 ,故选B.
4、某公路上的测速仪,在某一时间段内测得30辆汽车的速度(单位:km/h),其最大值和最小值分别是80,56.为了制作频数直方图,以5为组距,这样,可以把数据分成( )
A.4组 B.5组 C.6组 D.10组
解:(80﹣56)÷5
=24÷5
=4…4,
故可以把数据分成5组,
故选:B.
5、市某视力健康管理中心对全市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数直方图,则这组数据的组数与组距分别是( )
A.4和0.20 B.4和0.30 C.5和0.20 D.5和0.30
【答案】D
【分析】根据把所有数据分成若干组,分成的组的个数称为组数,每个小组的两个端点之间的距离称为组距,看图即可.
解:观察图形可得:有五组数据,因此组数为5;
组距=4.253.95=0.30
故答案选D
6、为了了解某校七年级800名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为:60≤x<80),则以下说法正确的是( )
A.跳绳次数不少于100次的占80%
B.大多数学生跳绳次数在140﹣160范围内
C.跳绳次数最多的是160次
D.由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有84人
解:跳绳次数不少于100次的占(10+18+12)÷50×100%=80%,故选项A正确;
多数学生跳绳次数在120﹣140范围内,故选项B错误;
跳绳次数最多的小于160次,故选项C错误;
由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有:800×=64(人),故选项D错误;
故选:A.
7、某小区居民利用一健步行APP"开展健步走活动,为了解居民的健步走情况,小文同学调查了部分居民某天行走的步效(单位:千步)。并将样本数据整理绘制成如下不完整的频率分布直方图和扇形统计图.
有下面四个推断:
①小文此次一共调查了200位小区居民;
②行走步效为千步的人数超过调查总人数的一半;
③行走步教为千步的人数为50人。④行走步数为12-16千步的扇形目心角是
根据统计图提供的信息.上述推断合理的是( )
A.①②③ B.①②④ C.①③④ D.②③④
解析:①小文此次一共调查(位)小区居民,正确
②行走步数为千步的人数为70,未超过调查总人数的一半,错误
③行走步数为千步的人数为(人),正确
④行走步数为千步的扇形圆心角是,正确.
故选C.
8、某班有48名同学,在一次数学检测中,分数均为整数,其成绩绘制成的频数直方图如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则分数在70.5~80.5之间的人数是( )
A.12 B.16 C.24 D.18
【答案】D
【分析】小长方形的高度比等于各组的人数比,即可求得分数在70.5到80.5之间的人数所占的比例,乘以总数48即可得出答案.
【详解】解:分数在70.5到80.5之间的人数是:×48=18(人);
故选:D.
9、2016年4月30日至5月2日,河北省共接待游客1708.3万人次,实现旅游收入106.5亿元,旅行社的小王想了解某企业员工个人的旅游年消费情况,他随机抽取部分员工进行调查,并将统计结果绘制成如表所示的频数分布表,则下列说法中不正确的是( )
个人旅游年 消费金额/元
频数
A.小王随机抽取了100名员工
B.在频数分布表中,组距是2000,组数是5组
C.个人旅游年消费金额在6000元以上的人数占随机抽取人数的22%
D.在随机抽取的员工中,个人旅游年消费金额在4000元以下(包括4000元)的共有37人
【答案】C
【分析】将所有的频数相加即可求得抽取的员工数;观察频数统计表即可求得组距和组数;根据统计表确定个人消费额在6000元以上的人数即可求得所占的百分比;将4000元以下的频数相加即可确定人数.
【详解】解:A、小王随机抽取了12+25+31+22+10=100人,故正确;
B、观察统计表发现频数分布表中,组距是2000,组数是5组,故正确;
C、个人旅游消费金额在6000元以上的人数占随机抽取人数的,故错误;
D、在随机抽取的员工中,个人旅游年消费金额在4000元以下的共有25+12=37人,故正确;
故选:C.
10、如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )
A.该班总人数为50人 B.步行人数为30人
C.乘车人数是骑车人数的2.5倍 D.骑车人数占20%
【解答】解:A、总人数是:25÷50%=50(人),故A正确;
B、步行的人数是:50×30%=15(人),故B错误;
C、骑车人数所占的比例是:1﹣50%﹣30%=20%,故D正确;
D、乘车人数是骑车人数倍数是:50%÷20%=2.5,故C正确.
由于该题选择错误的,故选:B.
二、填空题
11、将一个有80个数据的样本经统计分成6组,若某一组的频率为0.15,则该组的频数为 .
解:频数为80×0.15=12,
故答案为:12.
12、老师在黑板上随手写下一串数字“002 200 220”,则数字“0”出现的频率是_______.
【答案】
【分析】结合题意,根据频率的性质计算,即可得到答案.
【详解】根据题意,总共有9个数字,其中数字“0”出现5次
∴数字“0”出现的频率是:
故答案为:.
13、将一批数据分成5组,列出分布表,其中第二组与第五组的频率都是0.21,第一组与第三组的频率之和是0.44,那么第四组的频率是 .
【分析】根据频率的意义,各个小组的频率之和是1,已知其他小组的频率,计算可得第四组的频率.
【解答】解:由频率的意义可知,各个小组的频率之和是1,
则第四组的频率是1﹣0.44﹣0.21﹣0.21=0.14;
故答案为:0.14.
14、2020年綦江区中招体考已结束,数据显示,与去年相比,体考成绩略有下滑.今年某中学某班学生体育毕业考试的成绩(成绩取整数),制成如图所示的频数分布直方图,若成绩在44.5~47.5分范围内为良好,则该班学生体育成绩良好的百分率是 .
解:该班学生体育成绩良好的百分率是:×100%=40%.
故答案为:40%.
15、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷,收集整理数据后列频数分布表(部分)如下:
项目 乒乓球 羽毛球 篮球 足球
频数 80 50
百分比 40%
25% m
则表格中m的值为 .
【分析】先根据乒乓球的频数及频率求得被调查的学生总数,再用羽毛球人数除以总人数求得其百分比,继而根据百分比之和为1可得m的值.
【解答】解:由表可知被调查的学生总数为80÷0.4=200,
∴羽毛球的人数所占百分比为100%=25%,
则m=1﹣(40%+25%+25%)=10%,
故答案为:10%.
16、某学校为了解本校2000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时) 0≤x≤1 1<x≤2 2<x≤3 x>3
人数 7 10 14 19
解:2000×=680,
所以估计全校每周课外阅读时间不超过2小时的学生有680人.
故答案为680.
17、在100个数据中,用适当方法抽取50个样本进行统计,在频数分布表中,54.5~57.5这一组的频率是0.2,那么估计总体数据落在54.5~57.5之间的约有 个.
【分析】根据频率、频数的关系进行计算即可.
【解答】解:用样本估计总体:在频数分布表中,54.5~57.5这一组的频率是0.2,
估计总体数据落在54.5~57.5这一组的频率同样是0.2,
那么总体数据落在54.5~57.5之间的约有100×0.2=20个.
故答案为:20.
18、今年3月,上海市开展了在线学习,同时号召同学们在家要坚持体育锻炼,已知某班学生一周内在家锻炼时间的频数分布直方图如图所示.如果锻炼时间在0﹣2小时的学生的频率是20%,那么锻炼时间在4﹣6小时的学生的频率是 .
解:∵锻炼时间在0﹣2小时的学生的频率是20%,人数为8,
∴被调查的总人数为8÷20%=40(人),
则锻炼时间在4﹣6小时的学生的频率是10÷40=0.25,
故答案为:0.25.
19、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
【解答】解:观察直方图可知:
因为该样本中体重不小于55kg的频数为:9+5+2=16,
所以该样本中体重不小于55kg的频率是=0.4.
故答案为:0.4.
20、某中学七年级甲、乙两个班参加了一次数学考试,每班的考试人数都为40人,每个班的考试成绩分
为 A、B、C、D、E五个等级,现将两个班数学考试成绩统计如下:
根据以上统计图提供的信息,可知两个班人数相等的等级是__________.
【答案】A
【分析】根据扇形统计图把乙班每个等级的人数求出即可解答.
【详解】解:甲班各等级人数分别为:A等级:2人;B等级:5人;C等级:12人;D等级:13人;
E等级:8人;
乙班各等级人数:A等级:40×5%=2人;
B等级:40×10%=4人;
C等级:40×35%=14人;
D、E等级:40×25%=10人;
所以两个班A等级的人数相等,
故答案为:A.
三、解答题
21、八甲班进行了一次数学考试,将成绩绘制成了如下不完整的频数分布表和频数直方图:
(1)求频数分布表中a和b的值;
(2)将频数直方图补充完整;
(3)成绩不低于60分为及格,该班本次数学考试的及格率是多少?
成绩 频数(人数) 频率
50≤x<60 5 0.1
60≤x<70 10 0.2
70≤x<80 20 0.4
80≤x<90 a 0.2
90≤x<100 5 b
解:(1)八甲班的学生有:5÷0.1=50(人),
a=50×0.2=10,b=5÷50=0.1,
即频数分布表中a和b的值分别为10,0.1;
(2)由(1)知,a=10,
补全的频数分布直方图如右图所示;
(3)(1﹣0.1)×100%=0.9×100%=90%,
即该班本次数学考试的及格率是90%.
22、随着车辆的增加,交通违规的现象越来越严重.交警对某雷达测速区监测到的一组汽车的时速数据进行整理,得到其频数及频率如表
数据段 频数 频率
30~40 10 0.05
40~50 36
50~60
0.39
60~70 56
70~80 20 0.10
总计 200 1
注:30~40为时速大于30千米而小于40千米,其他类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
【答案】(1)第二行0.18,第三行78,第四行0.28;(2)见解析;(3)76
【分析】(1)根据频数÷总数=频率进行计算即可;
(2)结合(1)中的数据补全图形即可;
(3)根据频数分布直方图可看出汽车时速不低于60千米的车的数量.
(1)解:(1)36÷200=0.18,
200×0.39=78,
200-10-36-78-20=56,
56÷200=0.28;
故第二行0.18,第三行78,第四行0.28
(2)如图所示
(3)违章车辆数:56+20=76(辆).
答:违章车辆有76辆.
23、某公司共有400名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成统计图表进行分析.频数分布表
组别 销售数量(件) 频数 频率
A 20≤x<40 3 0.06
B 40≤x<60 7 0.14
C 60≤x<80 12 a
D 80≤x<100 m 0.48
E 100≤x<120 4 0.08
合计 b 1
请根据以上信息,解决下列问题:
(1)频数分布表中,a= 、b= ;
(2)补全频数分布直方图;
(3)如果该季度销量不低于100件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.
解:(1)b=3÷0.06=50,a=12÷50=0.24,
故答案为:0.24,50;
(2)m=50×0.48=24,补全频数分布直方图如下:
(3)400×0.08=32(人),
答:该季度被评为“优秀员工”的人数为32人.
24、为庆祝中华人民共和国成立70周年,郑州市某校组织八年级学生进行“方阵表演”.为了整齐划一,需了解学生的身高,现随机抽取该校八年级学生进行抽样调查,根据所得数据绘制出如下统计图表
组别 身高
A
B
C
D
E
根据图表提供的信息,回答下列问题:
(1)这次抽样调查,一共抽取学生_________人;
(2)扇形统计图中,扇形E的圆心角度数是_________;
(3)请补全频数分布直方图;
(4)已知该校八年级共有学生400人,请估计身高在的学生约有多少人?
【答案】(1)40;(2);(3)见解析;(4)估计身高在的学生约有80人
【分析】(1)用A组人数×其所占的百分数即可得到结论;
(2)利用乘以对应的比例即可求解;
(3)根据题意补全频数分布直方图即可;
(4)利用总人数400乘以对应的比例.
解:(1)这次抽样调查,一共抽取学生(人);
(2)扇形统计图中,扇形E的圆心角度数是,
故答案为:40;;
(3)身高在的人数为:人,
补全频数分布直方图如图所示;
(4)(人),
答:估计身高在的学生约有180人.
25、为弘扬中华传统文化,某校组织七年级名学生参加汉字听写大赛,为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为分)进行统计分析,得到如下所示的频数分布表:
分数段
频数
所占百分比
请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查的样本容量为_______,表中_______,_______;
(2)补全频数分布直方图;
(3)若成绩超过分为优秀,估计该校七年级学生中汉字听写能力为优秀的约有多少人?
【答案】(1)200、80、12%; (2)补全图形见解析;(3)该校八年级学生中汉字听写能力优秀的约有416人.
【分析】(1)根据第一组的频数是16,频率是0.08,即可求得总数,即样本容量,再根据小组频率求解 根据小组频数求解;
(2)根据(1)的计算结果画出作出直方图即可;
(3)利用总数800乘以优秀的人数所占的频率即可.
【详解】解:(1)样本容量是:16÷0.08=200;
所以
故答案为:200、80、12%;
(2)由 补全频数分布直方图,如下:
(3)由题意得:800×(0.4+0.12)=416(人).
答:该校八年级学生中汉字听写能力优秀的约有416人.
一、选择题
1、将40个数据分成五组,编成组号为①~⑤的五个组,频数分布如表:
组号 ① ② ③ ④ ⑤
频数 12 4 6
10
则第4组的频率是( )
A.0.2 B.0.3 C.8 D.12
2、一组数据共60个,分为6组,第1至第4组的频数分别为6,8,9,11,第5组的频率为0.20,则第6组的频数为( )
A.11 B.13 C.14 D.15
3、在全班45人中进行了你最喜爱的电视节目的调查活动,喜爱的电视剧有人数为18人,喜爱动画片有人数为15人,喜爱体育节目有人数为10人,则下列说法正确的是( )
A.喜爱的电视剧的人数的频率是 B.喜爱的电视剧的人数的频率是
C.喜爱的动画片的人数的频率是 D.喜爱的体育节目的人数的频率是
4、某公路上的测速仪,在某一时间段内测得30辆汽车的速度(单位:km/h),其最大值和最小值分别是80,56.为了制作频数直方图,以5为组距,这样,可以把数据分成( )
A.4组 B.5组 C.6组 D.10组
5、市某视力健康管理中心对全市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数直方图,则这组数据的组数与组距分别是( )
A.4和0.20 B.4和0.30 C.5和0.20 D.5和0.30
6、为了了解某校七年级800名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为:60≤x<80),则以下说法正确的是( )
A.跳绳次数不少于100次的占80%
B.大多数学生跳绳次数在140﹣160范围内
C.跳绳次数最多的是160次
D.由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有84人
7、某小区居民利用一健步行APP"开展健步走活动,为了解居民的健步走情况,小文同学调查了部分居民某天行走的步效(单位:千步)。并将样本数据整理绘制成如下不完整的频率分布直方图和扇形统计图.
有下面四个推断:
①小文此次一共调查了200位小区居民;
②行走步效为千步的人数超过调查总人数的一半;
③行走步教为千步的人数为50人。④行走步数为12-16千步的扇形目心角是
根据统计图提供的信息.上述推断合理的是( )
A.①②③ B.①②④ C.①③④ D.②③④
8、某班有48名同学,在一次数学检测中,分数均为整数,其成绩绘制成的频数直方图如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则分数在70.5~80.5之间的人数是( )
A.12 B.16 C.24 D.18
9、2016年4月30日至5月2日,河北省共接待游客1708.3万人次,实现旅游收入106.5亿元,旅行社的小王想了解某企业员工个人的旅游年消费情况,他随机抽取部分员工进行调查,并将统计结果绘制成如表所示的频数分布表,则下列说法中不正确的是( )
个人旅游年 消费金额/元
频数
A.小王随机抽取了100名员工
B.在频数分布表中,组距是2000,组数是5组
C.个人旅游年消费金额在6000元以上的人数占随机抽取人数的22%
D.在随机抽取的员工中,个人旅游年消费金额在4000元以下(包括4000元)的共有37人
10、如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )
A.该班总人数为50人 B.步行人数为30人
C.乘车人数是骑车人数的2.5倍 D.骑车人数占20%
二、填空题
11、将一个有80个数据的样本经统计分成6组,若某一组的频率为0.15,则该组的频数为 .
12、老师在黑板上随手写下一串数字“002 200 220”,则数字“0”出现的频率是_______.
13、将一批数据分成5组,列出分布表,其中第二组与第五组的频率都是0.21,第一组与第三组的频率之和是0.44,那么第四组的频率是 .
14、2020年綦江区中招体考已结束,数据显示,与去年相比,体考成绩略有下滑.今年某中学某班学生体育毕业考试的成绩(成绩取整数),制成如图所示的频数分布直方图,若成绩在44.5~47.5分范围内为良好,则该班学生体育成绩良好的百分率是 .
15、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷,收集整理数据后列频数分布表(部分)如下:
项目 乒乓球 羽毛球 篮球 足球
频数 80 50
百分比 40%
25% m
则表格中m的值为 .
16、某学校为了解本校2000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时) 0≤x≤1 1<x≤2 2<x≤3 x>3
人数 7 10 14 19
17、在100个数据中,用适当方法抽取50个样本进行统计,在频数分布表中,54.5~57.5这一组的频率是0.2,那么估计总体数据落在54.5~57.5之间的约有 个.
18、今年3月,上海市开展了在线学习,同时号召同学们在家要坚持体育锻炼,已知某班学生一周内在家锻炼时间的频数分布直方图如图所示.如果锻炼时间在0﹣2小时的学生的频率是20%,那么锻炼时间在4﹣6小时的学生的频率是 .
19、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
20、某中学七年级甲、乙两个班参加了一次数学考试,每班的考试人数都为40人,每个班的考试成绩分
为 A、B、C、D、E五个等级,现将两个班数学考试成绩统计如下:
根据以上统计图提供的信息,可知两个班人数相等的等级是__________.
三、解答题
21、八甲班进行了一次数学考试,将成绩绘制成了如下不完整的频数分布表和频数直方图:
(1)求频数分布表中a和b的值;
(2)将频数直方图补充完整;
(3)成绩不低于60分为及格,该班本次数学考试的及格率是多少?
成绩 频数(人数) 频率
50≤x<60 5 0.1
60≤x<70 10 0.2
70≤x<80 20 0.4
80≤x<90 a 0.2
90≤x<100 5 b
22、随着车辆的增加,交通违规的现象越来越严重.交警对某雷达测速区监测到的一组汽车的时速数据进行整理,得到其频数及频率如表
数据段 频数 频率
30~40 10 0.05
40~50 36
50~60
0.39
60~70 56
70~80 20 0.10
总计 200 1
注:30~40为时速大于30千米而小于40千米,其他类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
23、某公司共有400名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成统计图表进行分析.频数分布表
组别 销售数量(件) 频数 频率
A 20≤x<40 3 0.06
B 40≤x<60 7 0.14
C 60≤x<80 12 a
D 80≤x<100 m 0.48
E 100≤x<120 4 0.08
合计 b 1
请根据以上信息,解决下列问题:
(1)频数分布表中,a= 、b= ;
(2)补全频数分布直方图;
(3)如果该季度销量不低于100件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.
24、为庆祝中华人民共和国成立70周年,郑州市某校组织八年级学生进行“方阵表演”.为了整齐划一,需了解学生的身高,现随机抽取该校八年级学生进行抽样调查,根据所得数据绘制出如下统计图表
组别 身高
A
B
C
D
E
根据图表提供的信息,回答下列问题:
(1)这次抽样调查,一共抽取学生_________人;
(2)扇形统计图中,扇形E的圆心角度数是_________;
(3)请补全频数分布直方图;
(4)已知该校八年级共有学生400人,请估计身高在的学生约有多少人?
25、为弘扬中华传统文化,某校组织七年级名学生参加汉字听写大赛,为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为分)进行统计分析,得到如下所示的频数分布表:
分数段
频数
所占百分比
请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查的样本容量为_______,表中_______,_______;
(2)补全频数分布直方图;
(3)若成绩超过分为优秀,估计该校七年级学生中汉字听写能力为优秀的约有多少人?
专题复习提升训练卷10.2直方图-20-21人教版七年级数学下册(解析)
一、选择题
1、将40个数据分成五组,编成组号为①~⑤的五个组,频数分布如表:
组号 ① ② ③ ④ ⑤
频数 12 4 6
10
则第4组的频率是( )
A.0.2 B.0.3 C.8 D.12
解:根据频数分布表中的数据可知:
第4组的频数为:40﹣12﹣4﹣6﹣10=8,
所以第4组的频率为:8÷40=0.2.
故选:A.
2、一组数据共60个,分为6组,第1至第4组的频数分别为6,8,9,11,第5组的频率为0.20,则第6组的频数为( )
A.11 B.13 C.14 D.15
【答案】C
【分析】首先根据频数=总数×频率,求得第五组频数;再根据各组的频数和等于总数,求得第六组的频数.
【详解】解:根据题意,得
第五组频数是60×0.20=12,
故第六组的频数是60-6-8-9-11-12=14.
故选:C.
3、在全班45人中进行了你最喜爱的电视节目的调查活动,喜爱的电视剧有人数为18人,喜爱动画片有人数为15人,喜爱体育节目有人数为10人,则下列说法正确的是( )
A.喜爱的电视剧的人数的频率是 B.喜爱的电视剧的人数的频率是
C.喜爱的动画片的人数的频率是 D.喜爱的体育节目的人数的频率是
【答案】B
【解析】频率应为频数除以总数,所以喜欢看电视剧、动画片和体育节目的频率分别是、、 ,故选B.
4、某公路上的测速仪,在某一时间段内测得30辆汽车的速度(单位:km/h),其最大值和最小值分别是80,56.为了制作频数直方图,以5为组距,这样,可以把数据分成( )
A.4组 B.5组 C.6组 D.10组
解:(80﹣56)÷5
=24÷5
=4…4,
故可以把数据分成5组,
故选:B.
5、市某视力健康管理中心对全市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数直方图,则这组数据的组数与组距分别是( )
A.4和0.20 B.4和0.30 C.5和0.20 D.5和0.30
【答案】D
【分析】根据把所有数据分成若干组,分成的组的个数称为组数,每个小组的两个端点之间的距离称为组距,看图即可.
解:观察图形可得:有五组数据,因此组数为5;
组距=4.253.95=0.30
故答案选D
6、为了了解某校七年级800名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为:60≤x<80),则以下说法正确的是( )
A.跳绳次数不少于100次的占80%
B.大多数学生跳绳次数在140﹣160范围内
C.跳绳次数最多的是160次
D.由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有84人
解:跳绳次数不少于100次的占(10+18+12)÷50×100%=80%,故选项A正确;
多数学生跳绳次数在120﹣140范围内,故选项B错误;
跳绳次数最多的小于160次,故选项C错误;
由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有:800×=64(人),故选项D错误;
故选:A.
7、某小区居民利用一健步行APP"开展健步走活动,为了解居民的健步走情况,小文同学调查了部分居民某天行走的步效(单位:千步)。并将样本数据整理绘制成如下不完整的频率分布直方图和扇形统计图.
有下面四个推断:
①小文此次一共调查了200位小区居民;
②行走步效为千步的人数超过调查总人数的一半;
③行走步教为千步的人数为50人。④行走步数为12-16千步的扇形目心角是
根据统计图提供的信息.上述推断合理的是( )
A.①②③ B.①②④ C.①③④ D.②③④
解析:①小文此次一共调查(位)小区居民,正确
②行走步数为千步的人数为70,未超过调查总人数的一半,错误
③行走步数为千步的人数为(人),正确
④行走步数为千步的扇形圆心角是,正确.
故选C.
8、某班有48名同学,在一次数学检测中,分数均为整数,其成绩绘制成的频数直方图如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则分数在70.5~80.5之间的人数是( )
A.12 B.16 C.24 D.18
【答案】D
【分析】小长方形的高度比等于各组的人数比,即可求得分数在70.5到80.5之间的人数所占的比例,乘以总数48即可得出答案.
【详解】解:分数在70.5到80.5之间的人数是:×48=18(人);
故选:D.
9、2016年4月30日至5月2日,河北省共接待游客1708.3万人次,实现旅游收入106.5亿元,旅行社的小王想了解某企业员工个人的旅游年消费情况,他随机抽取部分员工进行调查,并将统计结果绘制成如表所示的频数分布表,则下列说法中不正确的是( )
个人旅游年 消费金额/元
频数
A.小王随机抽取了100名员工
B.在频数分布表中,组距是2000,组数是5组
C.个人旅游年消费金额在6000元以上的人数占随机抽取人数的22%
D.在随机抽取的员工中,个人旅游年消费金额在4000元以下(包括4000元)的共有37人
【答案】C
【分析】将所有的频数相加即可求得抽取的员工数;观察频数统计表即可求得组距和组数;根据统计表确定个人消费额在6000元以上的人数即可求得所占的百分比;将4000元以下的频数相加即可确定人数.
【详解】解:A、小王随机抽取了12+25+31+22+10=100人,故正确;
B、观察统计表发现频数分布表中,组距是2000,组数是5组,故正确;
C、个人旅游消费金额在6000元以上的人数占随机抽取人数的,故错误;
D、在随机抽取的员工中,个人旅游年消费金额在4000元以下的共有25+12=37人,故正确;
故选:C.
10、如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )
A.该班总人数为50人 B.步行人数为30人
C.乘车人数是骑车人数的2.5倍 D.骑车人数占20%
【解答】解:A、总人数是:25÷50%=50(人),故A正确;
B、步行的人数是:50×30%=15(人),故B错误;
C、骑车人数所占的比例是:1﹣50%﹣30%=20%,故D正确;
D、乘车人数是骑车人数倍数是:50%÷20%=2.5,故C正确.
由于该题选择错误的,故选:B.
二、填空题
11、将一个有80个数据的样本经统计分成6组,若某一组的频率为0.15,则该组的频数为 .
解:频数为80×0.15=12,
故答案为:12.
12、老师在黑板上随手写下一串数字“002 200 220”,则数字“0”出现的频率是_______.
【答案】
【分析】结合题意,根据频率的性质计算,即可得到答案.
【详解】根据题意,总共有9个数字,其中数字“0”出现5次
∴数字“0”出现的频率是:
故答案为:.
13、将一批数据分成5组,列出分布表,其中第二组与第五组的频率都是0.21,第一组与第三组的频率之和是0.44,那么第四组的频率是 .
【分析】根据频率的意义,各个小组的频率之和是1,已知其他小组的频率,计算可得第四组的频率.
【解答】解:由频率的意义可知,各个小组的频率之和是1,
则第四组的频率是1﹣0.44﹣0.21﹣0.21=0.14;
故答案为:0.14.
14、2020年綦江区中招体考已结束,数据显示,与去年相比,体考成绩略有下滑.今年某中学某班学生体育毕业考试的成绩(成绩取整数),制成如图所示的频数分布直方图,若成绩在44.5~47.5分范围内为良好,则该班学生体育成绩良好的百分率是 .
解:该班学生体育成绩良好的百分率是:×100%=40%.
故答案为:40%.
15、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷,收集整理数据后列频数分布表(部分)如下:
项目 乒乓球 羽毛球 篮球 足球
频数 80 50
百分比 40%
25% m
则表格中m的值为 .
【分析】先根据乒乓球的频数及频率求得被调查的学生总数,再用羽毛球人数除以总人数求得其百分比,继而根据百分比之和为1可得m的值.
【解答】解:由表可知被调查的学生总数为80÷0.4=200,
∴羽毛球的人数所占百分比为100%=25%,
则m=1﹣(40%+25%+25%)=10%,
故答案为:10%.
16、某学校为了解本校2000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时) 0≤x≤1 1<x≤2 2<x≤3 x>3
人数 7 10 14 19
解:2000×=680,
所以估计全校每周课外阅读时间不超过2小时的学生有680人.
故答案为680.
17、在100个数据中,用适当方法抽取50个样本进行统计,在频数分布表中,54.5~57.5这一组的频率是0.2,那么估计总体数据落在54.5~57.5之间的约有 个.
【分析】根据频率、频数的关系进行计算即可.
【解答】解:用样本估计总体:在频数分布表中,54.5~57.5这一组的频率是0.2,
估计总体数据落在54.5~57.5这一组的频率同样是0.2,
那么总体数据落在54.5~57.5之间的约有100×0.2=20个.
故答案为:20.
18、今年3月,上海市开展了在线学习,同时号召同学们在家要坚持体育锻炼,已知某班学生一周内在家锻炼时间的频数分布直方图如图所示.如果锻炼时间在0﹣2小时的学生的频率是20%,那么锻炼时间在4﹣6小时的学生的频率是 .
解:∵锻炼时间在0﹣2小时的学生的频率是20%,人数为8,
∴被调查的总人数为8÷20%=40(人),
则锻炼时间在4﹣6小时的学生的频率是10÷40=0.25,
故答案为:0.25.
19、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
【解答】解:观察直方图可知:
因为该样本中体重不小于55kg的频数为:9+5+2=16,
所以该样本中体重不小于55kg的频率是=0.4.
故答案为:0.4.
20、某中学七年级甲、乙两个班参加了一次数学考试,每班的考试人数都为40人,每个班的考试成绩分
为 A、B、C、D、E五个等级,现将两个班数学考试成绩统计如下:
根据以上统计图提供的信息,可知两个班人数相等的等级是__________.
【答案】A
【分析】根据扇形统计图把乙班每个等级的人数求出即可解答.
【详解】解:甲班各等级人数分别为:A等级:2人;B等级:5人;C等级:12人;D等级:13人;
E等级:8人;
乙班各等级人数:A等级:40×5%=2人;
B等级:40×10%=4人;
C等级:40×35%=14人;
D、E等级:40×25%=10人;
所以两个班A等级的人数相等,
故答案为:A.
三、解答题
21、八甲班进行了一次数学考试,将成绩绘制成了如下不完整的频数分布表和频数直方图:
(1)求频数分布表中a和b的值;
(2)将频数直方图补充完整;
(3)成绩不低于60分为及格,该班本次数学考试的及格率是多少?
成绩 频数(人数) 频率
50≤x<60 5 0.1
60≤x<70 10 0.2
70≤x<80 20 0.4
80≤x<90 a 0.2
90≤x<100 5 b
解:(1)八甲班的学生有:5÷0.1=50(人),
a=50×0.2=10,b=5÷50=0.1,
即频数分布表中a和b的值分别为10,0.1;
(2)由(1)知,a=10,
补全的频数分布直方图如右图所示;
(3)(1﹣0.1)×100%=0.9×100%=90%,
即该班本次数学考试的及格率是90%.
22、随着车辆的增加,交通违规的现象越来越严重.交警对某雷达测速区监测到的一组汽车的时速数据进行整理,得到其频数及频率如表
数据段 频数 频率
30~40 10 0.05
40~50 36
50~60
0.39
60~70 56
70~80 20 0.10
总计 200 1
注:30~40为时速大于30千米而小于40千米,其他类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
【答案】(1)第二行0.18,第三行78,第四行0.28;(2)见解析;(3)76
【分析】(1)根据频数÷总数=频率进行计算即可;
(2)结合(1)中的数据补全图形即可;
(3)根据频数分布直方图可看出汽车时速不低于60千米的车的数量.
(1)解:(1)36÷200=0.18,
200×0.39=78,
200-10-36-78-20=56,
56÷200=0.28;
故第二行0.18,第三行78,第四行0.28
(2)如图所示
(3)违章车辆数:56+20=76(辆).
答:违章车辆有76辆.
23、某公司共有400名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成统计图表进行分析.频数分布表
组别 销售数量(件) 频数 频率
A 20≤x<40 3 0.06
B 40≤x<60 7 0.14
C 60≤x<80 12 a
D 80≤x<100 m 0.48
E 100≤x<120 4 0.08
合计 b 1
请根据以上信息,解决下列问题:
(1)频数分布表中,a= 、b= ;
(2)补全频数分布直方图;
(3)如果该季度销量不低于100件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.
解:(1)b=3÷0.06=50,a=12÷50=0.24,
故答案为:0.24,50;
(2)m=50×0.48=24,补全频数分布直方图如下:
(3)400×0.08=32(人),
答:该季度被评为“优秀员工”的人数为32人.
24、为庆祝中华人民共和国成立70周年,郑州市某校组织八年级学生进行“方阵表演”.为了整齐划一,需了解学生的身高,现随机抽取该校八年级学生进行抽样调查,根据所得数据绘制出如下统计图表
组别 身高
A
B
C
D
E
根据图表提供的信息,回答下列问题:
(1)这次抽样调查,一共抽取学生_________人;
(2)扇形统计图中,扇形E的圆心角度数是_________;
(3)请补全频数分布直方图;
(4)已知该校八年级共有学生400人,请估计身高在的学生约有多少人?
【答案】(1)40;(2);(3)见解析;(4)估计身高在的学生约有80人
【分析】(1)用A组人数×其所占的百分数即可得到结论;
(2)利用乘以对应的比例即可求解;
(3)根据题意补全频数分布直方图即可;
(4)利用总人数400乘以对应的比例.
解:(1)这次抽样调查,一共抽取学生(人);
(2)扇形统计图中,扇形E的圆心角度数是,
故答案为:40;;
(3)身高在的人数为:人,
补全频数分布直方图如图所示;
(4)(人),
答:估计身高在的学生约有180人.
25、为弘扬中华传统文化,某校组织七年级名学生参加汉字听写大赛,为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为分)进行统计分析,得到如下所示的频数分布表:
分数段
频数
所占百分比
请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查的样本容量为_______,表中_______,_______;
(2)补全频数分布直方图;
(3)若成绩超过分为优秀,估计该校七年级学生中汉字听写能力为优秀的约有多少人?
【答案】(1)200、80、12%; (2)补全图形见解析;(3)该校八年级学生中汉字听写能力优秀的约有416人.
【分析】(1)根据第一组的频数是16,频率是0.08,即可求得总数,即样本容量,再根据小组频率求解 根据小组频数求解;
(2)根据(1)的计算结果画出作出直方图即可;
(3)利用总数800乘以优秀的人数所占的频率即可.
【详解】解:(1)样本容量是:16÷0.08=200;
所以
故答案为:200、80、12%;
(2)由 补全频数分布直方图,如下:
(3)由题意得:800×(0.4+0.12)=416(人).
答:该校八年级学生中汉字听写能力优秀的约有416人.
