18.3平行四边形 单元复习(2)--2020-2021学年人教版八年级数学下册专题复习提升训练(Word版含解析)
文档属性
| 名称 | 18.3平行四边形 单元复习(2)--2020-2021学年人教版八年级数学下册专题复习提升训练(Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 00:00:00 | ||
图片预览

文档简介
专题复习提升训练卷18.3《平行四边形》单元训练(2)-20-21人教版八年级数学下册
一、选择题
1、如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CD
C.∠ABC=∠ADC,AD∥BC D.∠ABD=∠BDC,∠BAD=∠DCB
2、如图,在四边形ABCD中,对角线AC、BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90° B.AB=BD C.AC⊥BD D.AC=BD
3、如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长( )
A. B.2﹣2 C.2﹣ D.2
4、如图,在平行四边形ABCD中,,AC=2,BD=4,则BC的长是( )
A. B. C.3 D.5
5、如图,四边形ABCO为平行四边形,A,C两点的坐标分别是(3,0),(1,2),
则平行四边形ABCO的周长等于( )
A. B. C.4 D.6+2
6、如图,在△ABC中,点D是边BC上的点(与B、C两点不重合),过点D作DE//AC,DF//AB,分别交AB、AC于E、F两点,下列说法错误的是( )
A.四边形AEDF是平行四边形 B.若AD平分∠BAC,则四边形AEDF是菱形
C.若AB⊥AC,则四边形AEDF是矩形 D.若BD=CD,则四边形AEDF是正方形
7、如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,
则下列结论一定正确的是( )
A.∠DAB′=∠CAB′ B.∠ACD=∠B′CD C.AD=AE D.AE=CE
8、如图,在菱形ABCD中,对角线AC、BD交于点O,且AC=6,BD=8,过A点作AE垂直BC,交BC于点E,则的值为( )
A. B. C. D.
9、如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
10、如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,
则PE+PF的值为( )
A.4 B.2 C. D.2
二、填空题
11、如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,四边形BEFD周长为14,
则AB+BC的长为 .
12、如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足____________(关系)时,四边形EFGH为矩形.
13、如图,在矩形ABCD中,对角线AC与BD相交于点O,∠ACB=30°,BD=4,
则矩形ABCD的面积是 .
14、如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°.若AB=5,BC=8,
则EF的长为 .
15、如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交ED于点P.
若AE=AP=1,PB=,下列结论:①△APD≌△AEB;②EB⊥ED;③PD=,
其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
16、如图,菱形ABCD的边长AB=3,对角线BD=4,点E,F在BD上,且BE=DF=,连接AE,AF,CE,CF.则四边形AECF的周长为 .
17、如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE、BD于点P,过点P作PQ⊥BC于
点Q,则PQ= .
18、如图,在边长为6的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于E,MF⊥CD于F,
则EF的最小值为 .
19、如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,给出下列判断:
①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,
③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,
其中,结论正确的是__________(只需填写正确结论的序号).
20、如图,在正方形ABCD中,点M、N为边BC和CD上的动点(不含端点),∠MAN=45°,下列四个结论:①当MN=MC时,则∠BAM=22.5°;②2∠AMN﹣∠MNC=90°;③△MNC的周长不变;
④∠AMN﹣∠AMB=60°.其中正确结论的序号是 .
三、解答题
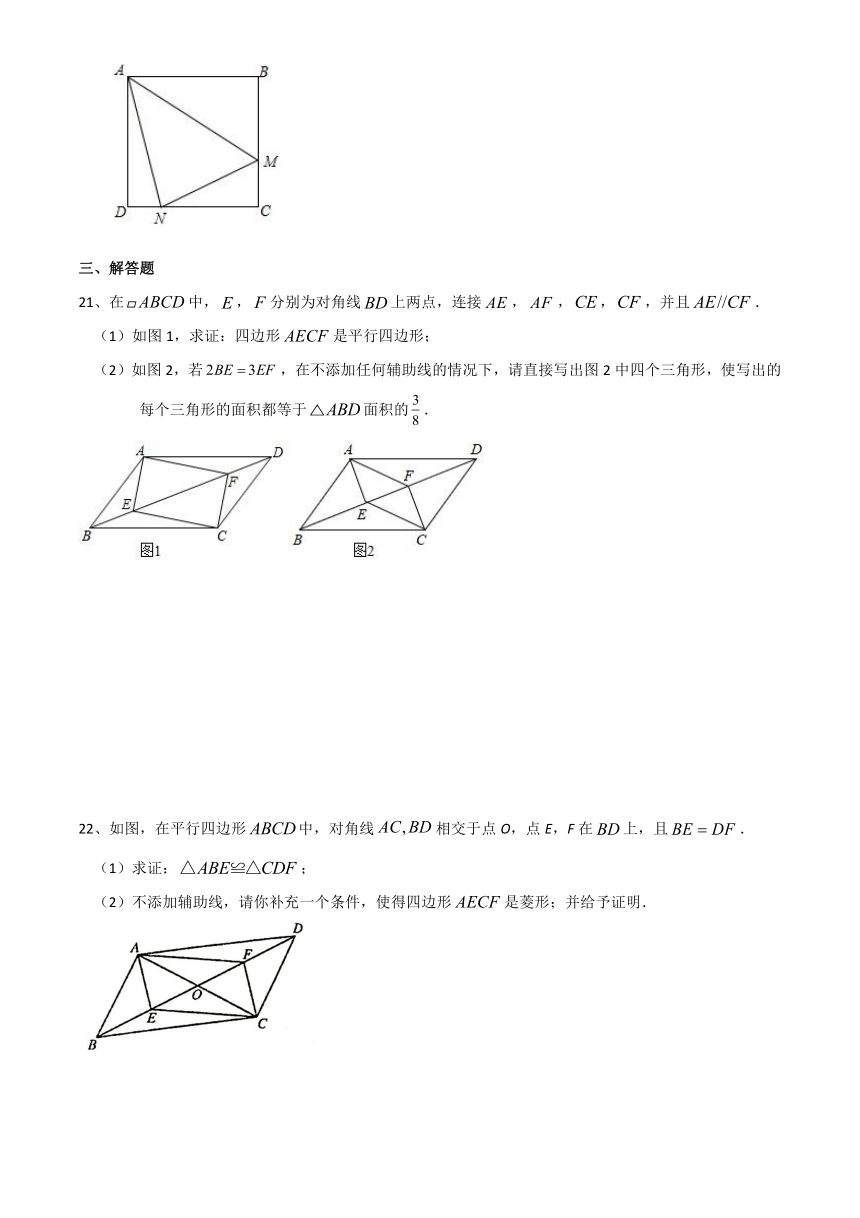
21、在中,,分别为对角线上两点,连接,,,,并且.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,若,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于面积的.
22、如图,在平行四边形中,对角线相交于点O,点E,F在上,且.
(1)求证:;
(2)不添加辅助线,请你补充一个条件,使得四边形是菱形;并给予证明.
23、△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB,AC于点F,G,连接BE.
(1)如图1所示,当点D在线段BC上时,探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图2所示,当点D在BC的延长线上运动到什么位置时,四边形BCGE是菱形?并说明理由.
24、如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.
(1)求证:EA是∠QED的平分线;
(2)已知BE=1,DF=3,求EF的长.
25、如图1,已知正方形的边在正方形的边上,连接、.
(1)试猜想与的位置关系和数量关系: , .
(2)将正方形绕点按顺时针方向旋转,使点落在边上,如图2,连接和.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
26、如图1,已知在四边形ABCD中,AD∥BC,AB∥CD,BE平分∠ABC,交AD于点E,过点E作EF∥AB,交BC于点F,O是BE的中点,连接OF,OC,OD.
(1)求证:四边形ABFE是菱形;
(2)若∠ABC=90°,如图2所示:
①求证:∠ADO=∠BCO;
②若∠EOD=15°,AE=1,求OC的长.
27、如图,在平行四边形中,的平分线交于点,交的延长线于,以、为邻边作平行四边形.
(1)证明平行四边形是菱形;
(2)若,连结、、,
①求证:;
②求的度数;
(3)若,,,是的中点,求的长.
专题复习提升训练卷18.3《平行四边形》单元训练(2)-20-21人教版八年级数学下册(答案)
一、选择题
1、如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( B )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CD
C.∠ABC=∠ADC,AD∥BC D.∠ABD=∠BDC,∠BAD=∠DCB
2、如图,在四边形ABCD中,对角线AC、BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( C )
A.∠ABC=90° B.AB=BD C.AC⊥BD D.AC=BD
3、如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长(B )
A. B.2﹣2 C.2﹣ D.2
4、如图,在平行四边形ABCD中,,AC=2,BD=4,则BC的长是( B )
A. B. C.3 D.5
5、如图,四边形ABCO为平行四边形,A,C两点的坐标分别是(3,0),(1,2),
则平行四边形ABCO的周长等于( D )
A. B. C.4 D.6+2
6、如图,在△ABC中,点D是边BC上的点(与B、C两点不重合),过点D作DE//AC,DF//AB,分别交AB、AC于E、F两点,下列说法错误的是( )
A.四边形AEDF是平行四边形 B.若AD平分∠BAC,则四边形AEDF是菱形
C.若AB⊥AC,则四边形AEDF是矩形 D.若BD=CD,则四边形AEDF是正方形
解:∵DE//AC,DF//AB,∴四边形AEDF是平行四边形,故选项A正确,不符合题意;
若AD平分∠BAC,则∠EAD=∠FAD,
又∵∠EAD=∠FDA,∴∠FAD=∠FDA,∴FA=FD,∴平行四边形AEDF是菱形,
故选项B正确,不符合题意;
∵AB⊥AC,∴平行四边形AEDF是矩形,故选项C正确,不符合题意;
若BD=CD,则四边形AEDF不一定是正方形;选项D错误,符合题意.
故选D.
7、如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,
则下列结论一定正确的是( )
A.∠DAB′=∠CAB′ B.∠ACD=∠B′CD C.AD=AE D.AE=CE
【解析】∵四边形ABCD为矩形,∴AB∥CD,∴∠ACD=∠BAC,
由折叠的性质可得∠BAC =∠EAC, ∴∠ACD=∠EAC,∴AE=CE. 故选D
8、如图,在菱形ABCD中,对角线AC、BD交于点O,且AC=6,BD=8,过A点作AE垂直BC,交BC于点E,则的值为( C )
A. B. C. D.
9、如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( D )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
10、如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,
则PE+PF的值为( C )
A.4 B.2 C. D.2
二、填空题
11、如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,四边形BEFD周长为14,
则AB+BC的长为 14 .
12、如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足____________(关系)时,四边形EFGH为矩形.
【解析】∵四边形ABCD是矩形,∴∠A=90°. ∵AE=AF,∴∠AFE=∠AEF=45°.
又∵EH⊥EF,FG⊥EF,∴∠GFB=∠HED=45°,∴△DHE和△BGF都是等腰直角三角形.
如果四边形EFGH是矩形,则EH=FG,∴ED=FB, 又∵AE=AF,∴AD=AB.
13、如图,在矩形ABCD中,对角线AC与BD相交于点O,∠ACB=30°,BD=4,
则矩形ABCD的面积是 4 .
14、如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°.若AB=5,BC=8,
则EF的长为 .
15、如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交ED于点P.
若AE=AP=1,PB=,下列结论:①△APD≌△AEB;②EB⊥ED;③PD=,
其中正确结论的序号是( A )
A.①② B.①③ C.②③ D.①②③
16、如图,菱形ABCD的边长AB=3,对角线BD=4,点E,F在BD上,且BE=DF=,连接AE,AF,CE,CF.则四边形AECF的周长为 4 .
17、如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE、BD于点P,过点P作PQ⊥BC于
点Q,则PQ= .
18、如图,在边长为6的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于E,MF⊥CD于F,
则EF的最小值为 3 .
19、如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,给出下列判断:
①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,
③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,
其中,结论正确的是__________(只需填写正确结论的序号).
【解析】①∵△AEF是等边三角形,∴∠EAF=60°,AE=AF,又∵AE⊥BC,AF⊥CD,∴∠C=120°,
∵四边形ABCD是平行四边形,∴AB∥CD,∠C=∠BAD=120°,
∴∠B=180°-∠C=60°,故①正确;
②∵∠D=∠B=60°,∴∠BAE=∠DAF=90°-60°=30°,∴∠EAF=120°-30°-30°=60°,
但是AE不一定等于AF,故②错误;
③若AE=AF,则BC·AE=CD·AF,∴BC=CD,∴平行四边形ABCD是菱形,故③正确;
④若平行四边形ABCD是菱形,则BC=CD,∴BC·AE=CD·AF,∴AE=AF,故④正确;
故答案为①③④.
20、如图,在正方形ABCD中,点M、N为边BC和CD上的动点(不含端点),∠MAN=45°,下列四个结论:①当MN=MC时,则∠BAM=22.5°;②2∠AMN﹣∠MNC=90°;③△MNC的周长不变;
④∠AMN﹣∠AMB=60°.其中正确结论的序号是 ①②③ .
三、解答题
21、在中,,分别为对角线上两点,连接,,,,并且.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,若,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于面积的.
【详解】(1)证明:如图1,
∵四边形为平行四边形,∴,,
∵,∴,∴,即,
∴,∴,∴四边形是平行四边形;
(2)由(1)可得,BE=DF,
∵,∴,
根据△ABD和△ABE、△ADF是等高,可得:△ABE、△ADF的面积是△ABD面积的,
∵四边形ABCD是平行四边形,∴△ABD和△BCD的面积相等,
同理可得△BEC和△DFC的面积是△BCD面积的,
∴,,,的面积都等于面积的.
22、如图,在平行四边形中,对角线相交于点O,点E,F在上,且.
(1)求证:;
(2)不添加辅助线,请你补充一个条件,使得四边形是菱形;并给予证明.
【详解】(1)证明:∵四边形是平行四边形,∴.∴.
又∵,∴.
(2)补充的条件是:.(答案不唯一)
证明:∵四边形是平行四边形,∴,.
∵,∴.∴四边形是平行四边形.
又∵,∴四边形是菱形.
23、△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB,AC于点F,G,连接BE.
(1)如图1所示,当点D在线段BC上时,探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图2所示,当点D在BC的延长线上运动到什么位置时,四边形BCGE是菱形?并说明理由.
解:(1)四边形BCGE是平行四边形.
理由:∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°.
又∵∠EAB=∠EAD-∠BAD,∠DAC=∠BAC-∠BAD,∴∠EAB=∠DAC.
∴△AEB≌△ADC(SAS).∴∠ABE=∠C=60°.
又∵∠BAC=∠C=60°,∴∠ABE=∠BAC.,∴EB∥GC.
又∵EG∥BC,∴四边形BCGE是平行四边形.
(2)当CD=CB(∠CAD=30°或∠BAD=90°或∠ADC=30°)时,四边形BCGE是菱形.
理由:由(1)得△AEB≌△ADC, ∴BE=CD,∠ACD=∠ABE=120°.
又∵∠ABC=∠ACB=∠DCG=60°,
∴∠EBC=∠ABE-∠ABC=120°-60°=60°=∠DCG. ∴BE∥CG.
又∵EG∥BC,∴四边形BCGE是平行四边形.
又∵CD=CB,∴BE=CD.
∴BE=BC,∴四边形BCGE是菱形.
24、如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.
(1)求证:EA是∠QED的平分线;
(2)已知BE=1,DF=3,求EF的长.
证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠BAQ=∠DAF,
∵∠EAF=45°,∴∠DAF+∠BAE=45°,∴∠QAE=45°,∴∠QAE=∠FAE,
在△AQE和△AFE中,,∴△AQE≌△AFE(SAS),
∴∠AEQ=∠AEF,∴EA是∠QED的平分线;
(2)由(1)得△AQE≌△AFE,∴QE=EF,∠ADF=∠ABQ,
∵四边形ABCD是正方形,∴∠ADB=∠ABD=45°,∴∠ABQ=45°,
∴∠QBE=∠ABQ+∠ABD=90°,
在Rt△QBE中,QB2+BE2=QE2,
又∵QB=DF,∴EF2=BE2+DF2=1+9=10,∴EF=.
25、如图1,已知正方形的边在正方形的边上,连接、.
(1)试猜想与的位置关系和数量关系: , .
(2)将正方形绕点按顺时针方向旋转,使点落在边上,如图2,连接和.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
【解析】(1)答:;
证明:如图1中,延长交于点.
在正方形与正方形中,,,,
,,,
,,
,.
故答案为,.
(2)答:成立;
证明:如图2中,延长和相交于点.
在正方形和正方形中,
,,,
;,,,
又,,,
又,,,
, .
26、如图1,已知在四边形ABCD中,AD∥BC,AB∥CD,BE平分∠ABC,交AD于点E,过点E作EF∥AB,交BC于点F,O是BE的中点,连接OF,OC,OD.
(1)求证:四边形ABFE是菱形;
(2)若∠ABC=90°,如图2所示:
①求证:∠ADO=∠BCO;
②若∠EOD=15°,AE=1,求OC的长.
解答:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,即AE∥BF,
∵EF∥AB,∴四边形ABFE是平行四边形,
∵AE∥BF,∴∠AEB=∠ABE,
∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠ABE=∠AEB,∴AB=AE,∴平行四边形ABFE是菱形;
(2)①证明:过O作ON∥BC交DC于N,如图2所示:
∵AD∥BC,AB∥CD,∠ABC=90°,∴四边形ABCD是矩形,∴∠ADC=∠BCD=90°,AD∥BC,
∴AD∥ON∥BC,
∵O为BE的中点,∴N为DC的中点,ON⊥DC,∴OD=OC,∴∠ODC=∠OCD,
∵∠ADC=∠BCD=90°,∴∠ADO=∠BCO;
②解:过O作OM作BC于M,如图3所示:
∵四边形ABFE是平行四边形,AB=AE,∠ABC=90°,∴四边形ABFE是正方形,
∴EF=BF=AE=1,∠BFE=90°,∠AEB=∠AEF=45°,
∵O为BE的中点,∴OF=BE=OB,
∵OM⊥BC,∴BM=FM,∴OM是△BEF的中位线,∴OM=EF=,
∵∠EOD=15°,∴∠ADO=∠AEB﹣∠EOD=45°﹣15°=30°,
由(2)得:∠BCO=∠ADO=30°,∴OC=2OM=1.
27、如图,在平行四边形中,的平分线交于点,交的延长线于,以、为邻边作平行四边形.
(1)证明平行四边形是菱形;
(2)若,连结、、,
①求证:;
②求的度数;
(3)若,,,是的中点,求的长.
【解析】(1)证明:平分,,
四边形是平行四边形,,,
,,,,
又四边形是平行四边形,四边形为菱形;
(2)①四边形是平行四边形,,,,
,,
由(1)知,四边形是菱形,,,
,,
,,
是的平分线,,
,,,
,,;
②,,,,
,是等边三角形,,,
,是等边三角形,;
(3)如图2中,连接,,
,四边形是平行四边形,四边形是矩形,
又由(1)可知四边形为菱形,,四边形为正方形.
,,
为中点,,,
在和中,,,
,.
,是等腰直角三角形.
,,,.
一、选择题
1、如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CD
C.∠ABC=∠ADC,AD∥BC D.∠ABD=∠BDC,∠BAD=∠DCB
2、如图,在四边形ABCD中,对角线AC、BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90° B.AB=BD C.AC⊥BD D.AC=BD
3、如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长( )
A. B.2﹣2 C.2﹣ D.2
4、如图,在平行四边形ABCD中,,AC=2,BD=4,则BC的长是( )
A. B. C.3 D.5
5、如图,四边形ABCO为平行四边形,A,C两点的坐标分别是(3,0),(1,2),
则平行四边形ABCO的周长等于( )
A. B. C.4 D.6+2
6、如图,在△ABC中,点D是边BC上的点(与B、C两点不重合),过点D作DE//AC,DF//AB,分别交AB、AC于E、F两点,下列说法错误的是( )
A.四边形AEDF是平行四边形 B.若AD平分∠BAC,则四边形AEDF是菱形
C.若AB⊥AC,则四边形AEDF是矩形 D.若BD=CD,则四边形AEDF是正方形
7、如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,
则下列结论一定正确的是( )
A.∠DAB′=∠CAB′ B.∠ACD=∠B′CD C.AD=AE D.AE=CE
8、如图,在菱形ABCD中,对角线AC、BD交于点O,且AC=6,BD=8,过A点作AE垂直BC,交BC于点E,则的值为( )
A. B. C. D.
9、如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
10、如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,
则PE+PF的值为( )
A.4 B.2 C. D.2
二、填空题
11、如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,四边形BEFD周长为14,
则AB+BC的长为 .
12、如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足____________(关系)时,四边形EFGH为矩形.
13、如图,在矩形ABCD中,对角线AC与BD相交于点O,∠ACB=30°,BD=4,
则矩形ABCD的面积是 .
14、如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°.若AB=5,BC=8,
则EF的长为 .
15、如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交ED于点P.
若AE=AP=1,PB=,下列结论:①△APD≌△AEB;②EB⊥ED;③PD=,
其中正确结论的序号是( )
A.①② B.①③ C.②③ D.①②③
16、如图,菱形ABCD的边长AB=3,对角线BD=4,点E,F在BD上,且BE=DF=,连接AE,AF,CE,CF.则四边形AECF的周长为 .
17、如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE、BD于点P,过点P作PQ⊥BC于
点Q,则PQ= .
18、如图,在边长为6的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于E,MF⊥CD于F,
则EF的最小值为 .
19、如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,给出下列判断:
①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,
③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,
其中,结论正确的是__________(只需填写正确结论的序号).
20、如图,在正方形ABCD中,点M、N为边BC和CD上的动点(不含端点),∠MAN=45°,下列四个结论:①当MN=MC时,则∠BAM=22.5°;②2∠AMN﹣∠MNC=90°;③△MNC的周长不变;
④∠AMN﹣∠AMB=60°.其中正确结论的序号是 .
三、解答题
21、在中,,分别为对角线上两点,连接,,,,并且.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,若,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于面积的.
22、如图,在平行四边形中,对角线相交于点O,点E,F在上,且.
(1)求证:;
(2)不添加辅助线,请你补充一个条件,使得四边形是菱形;并给予证明.
23、△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB,AC于点F,G,连接BE.
(1)如图1所示,当点D在线段BC上时,探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图2所示,当点D在BC的延长线上运动到什么位置时,四边形BCGE是菱形?并说明理由.
24、如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.
(1)求证:EA是∠QED的平分线;
(2)已知BE=1,DF=3,求EF的长.
25、如图1,已知正方形的边在正方形的边上,连接、.
(1)试猜想与的位置关系和数量关系: , .
(2)将正方形绕点按顺时针方向旋转,使点落在边上,如图2,连接和.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
26、如图1,已知在四边形ABCD中,AD∥BC,AB∥CD,BE平分∠ABC,交AD于点E,过点E作EF∥AB,交BC于点F,O是BE的中点,连接OF,OC,OD.
(1)求证:四边形ABFE是菱形;
(2)若∠ABC=90°,如图2所示:
①求证:∠ADO=∠BCO;
②若∠EOD=15°,AE=1,求OC的长.
27、如图,在平行四边形中,的平分线交于点,交的延长线于,以、为邻边作平行四边形.
(1)证明平行四边形是菱形;
(2)若,连结、、,
①求证:;
②求的度数;
(3)若,,,是的中点,求的长.
专题复习提升训练卷18.3《平行四边形》单元训练(2)-20-21人教版八年级数学下册(答案)
一、选择题
1、如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( B )
A.∠ABD=∠BDC,OA=OC B.∠ABC=∠ADC,AB=CD
C.∠ABC=∠ADC,AD∥BC D.∠ABD=∠BDC,∠BAD=∠DCB
2、如图,在四边形ABCD中,对角线AC、BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( C )
A.∠ABC=90° B.AB=BD C.AC⊥BD D.AC=BD
3、如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长(B )
A. B.2﹣2 C.2﹣ D.2
4、如图,在平行四边形ABCD中,,AC=2,BD=4,则BC的长是( B )
A. B. C.3 D.5
5、如图,四边形ABCO为平行四边形,A,C两点的坐标分别是(3,0),(1,2),
则平行四边形ABCO的周长等于( D )
A. B. C.4 D.6+2
6、如图,在△ABC中,点D是边BC上的点(与B、C两点不重合),过点D作DE//AC,DF//AB,分别交AB、AC于E、F两点,下列说法错误的是( )
A.四边形AEDF是平行四边形 B.若AD平分∠BAC,则四边形AEDF是菱形
C.若AB⊥AC,则四边形AEDF是矩形 D.若BD=CD,则四边形AEDF是正方形
解:∵DE//AC,DF//AB,∴四边形AEDF是平行四边形,故选项A正确,不符合题意;
若AD平分∠BAC,则∠EAD=∠FAD,
又∵∠EAD=∠FDA,∴∠FAD=∠FDA,∴FA=FD,∴平行四边形AEDF是菱形,
故选项B正确,不符合题意;
∵AB⊥AC,∴平行四边形AEDF是矩形,故选项C正确,不符合题意;
若BD=CD,则四边形AEDF不一定是正方形;选项D错误,符合题意.
故选D.
7、如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,
则下列结论一定正确的是( )
A.∠DAB′=∠CAB′ B.∠ACD=∠B′CD C.AD=AE D.AE=CE
【解析】∵四边形ABCD为矩形,∴AB∥CD,∴∠ACD=∠BAC,
由折叠的性质可得∠BAC =∠EAC, ∴∠ACD=∠EAC,∴AE=CE. 故选D
8、如图,在菱形ABCD中,对角线AC、BD交于点O,且AC=6,BD=8,过A点作AE垂直BC,交BC于点E,则的值为( C )
A. B. C. D.
9、如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( D )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
10、如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,
则PE+PF的值为( C )
A.4 B.2 C. D.2
二、填空题
11、如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,四边形BEFD周长为14,
则AB+BC的长为 14 .
12、如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足____________(关系)时,四边形EFGH为矩形.
【解析】∵四边形ABCD是矩形,∴∠A=90°. ∵AE=AF,∴∠AFE=∠AEF=45°.
又∵EH⊥EF,FG⊥EF,∴∠GFB=∠HED=45°,∴△DHE和△BGF都是等腰直角三角形.
如果四边形EFGH是矩形,则EH=FG,∴ED=FB, 又∵AE=AF,∴AD=AB.
13、如图,在矩形ABCD中,对角线AC与BD相交于点O,∠ACB=30°,BD=4,
则矩形ABCD的面积是 4 .
14、如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°.若AB=5,BC=8,
则EF的长为 .
15、如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交ED于点P.
若AE=AP=1,PB=,下列结论:①△APD≌△AEB;②EB⊥ED;③PD=,
其中正确结论的序号是( A )
A.①② B.①③ C.②③ D.①②③
16、如图,菱形ABCD的边长AB=3,对角线BD=4,点E,F在BD上,且BE=DF=,连接AE,AF,CE,CF.则四边形AECF的周长为 4 .
17、如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE、BD于点P,过点P作PQ⊥BC于
点Q,则PQ= .
18、如图,在边长为6的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于E,MF⊥CD于F,
则EF的最小值为 3 .
19、如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,给出下列判断:
①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,
③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,
其中,结论正确的是__________(只需填写正确结论的序号).
【解析】①∵△AEF是等边三角形,∴∠EAF=60°,AE=AF,又∵AE⊥BC,AF⊥CD,∴∠C=120°,
∵四边形ABCD是平行四边形,∴AB∥CD,∠C=∠BAD=120°,
∴∠B=180°-∠C=60°,故①正确;
②∵∠D=∠B=60°,∴∠BAE=∠DAF=90°-60°=30°,∴∠EAF=120°-30°-30°=60°,
但是AE不一定等于AF,故②错误;
③若AE=AF,则BC·AE=CD·AF,∴BC=CD,∴平行四边形ABCD是菱形,故③正确;
④若平行四边形ABCD是菱形,则BC=CD,∴BC·AE=CD·AF,∴AE=AF,故④正确;
故答案为①③④.
20、如图,在正方形ABCD中,点M、N为边BC和CD上的动点(不含端点),∠MAN=45°,下列四个结论:①当MN=MC时,则∠BAM=22.5°;②2∠AMN﹣∠MNC=90°;③△MNC的周长不变;
④∠AMN﹣∠AMB=60°.其中正确结论的序号是 ①②③ .
三、解答题
21、在中,,分别为对角线上两点,连接,,,,并且.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,若,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于面积的.
【详解】(1)证明:如图1,
∵四边形为平行四边形,∴,,
∵,∴,∴,即,
∴,∴,∴四边形是平行四边形;
(2)由(1)可得,BE=DF,
∵,∴,
根据△ABD和△ABE、△ADF是等高,可得:△ABE、△ADF的面积是△ABD面积的,
∵四边形ABCD是平行四边形,∴△ABD和△BCD的面积相等,
同理可得△BEC和△DFC的面积是△BCD面积的,
∴,,,的面积都等于面积的.
22、如图,在平行四边形中,对角线相交于点O,点E,F在上,且.
(1)求证:;
(2)不添加辅助线,请你补充一个条件,使得四边形是菱形;并给予证明.
【详解】(1)证明:∵四边形是平行四边形,∴.∴.
又∵,∴.
(2)补充的条件是:.(答案不唯一)
证明:∵四边形是平行四边形,∴,.
∵,∴.∴四边形是平行四边形.
又∵,∴四边形是菱形.
23、△ABC是等边三角形,点D是射线BC上的一个动点(点D不与点B,C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交射线AB,AC于点F,G,连接BE.
(1)如图1所示,当点D在线段BC上时,探究四边形BCGE是怎样特殊的四边形?并说明理由;
(2)如图2所示,当点D在BC的延长线上运动到什么位置时,四边形BCGE是菱形?并说明理由.
解:(1)四边形BCGE是平行四边形.
理由:∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°.
又∵∠EAB=∠EAD-∠BAD,∠DAC=∠BAC-∠BAD,∴∠EAB=∠DAC.
∴△AEB≌△ADC(SAS).∴∠ABE=∠C=60°.
又∵∠BAC=∠C=60°,∴∠ABE=∠BAC.,∴EB∥GC.
又∵EG∥BC,∴四边形BCGE是平行四边形.
(2)当CD=CB(∠CAD=30°或∠BAD=90°或∠ADC=30°)时,四边形BCGE是菱形.
理由:由(1)得△AEB≌△ADC, ∴BE=CD,∠ACD=∠ABE=120°.
又∵∠ABC=∠ACB=∠DCG=60°,
∴∠EBC=∠ABE-∠ABC=120°-60°=60°=∠DCG. ∴BE∥CG.
又∵EG∥BC,∴四边形BCGE是平行四边形.
又∵CD=CB,∴BE=CD.
∴BE=BC,∴四边形BCGE是菱形.
24、如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.
(1)求证:EA是∠QED的平分线;
(2)已知BE=1,DF=3,求EF的长.
证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠BAQ=∠DAF,
∵∠EAF=45°,∴∠DAF+∠BAE=45°,∴∠QAE=45°,∴∠QAE=∠FAE,
在△AQE和△AFE中,,∴△AQE≌△AFE(SAS),
∴∠AEQ=∠AEF,∴EA是∠QED的平分线;
(2)由(1)得△AQE≌△AFE,∴QE=EF,∠ADF=∠ABQ,
∵四边形ABCD是正方形,∴∠ADB=∠ABD=45°,∴∠ABQ=45°,
∴∠QBE=∠ABQ+∠ABD=90°,
在Rt△QBE中,QB2+BE2=QE2,
又∵QB=DF,∴EF2=BE2+DF2=1+9=10,∴EF=.
25、如图1,已知正方形的边在正方形的边上,连接、.
(1)试猜想与的位置关系和数量关系: , .
(2)将正方形绕点按顺时针方向旋转,使点落在边上,如图2,连接和.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
【解析】(1)答:;
证明:如图1中,延长交于点.
在正方形与正方形中,,,,
,,,
,,
,.
故答案为,.
(2)答:成立;
证明:如图2中,延长和相交于点.
在正方形和正方形中,
,,,
;,,,
又,,,
又,,,
, .
26、如图1,已知在四边形ABCD中,AD∥BC,AB∥CD,BE平分∠ABC,交AD于点E,过点E作EF∥AB,交BC于点F,O是BE的中点,连接OF,OC,OD.
(1)求证:四边形ABFE是菱形;
(2)若∠ABC=90°,如图2所示:
①求证:∠ADO=∠BCO;
②若∠EOD=15°,AE=1,求OC的长.
解答:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,即AE∥BF,
∵EF∥AB,∴四边形ABFE是平行四边形,
∵AE∥BF,∴∠AEB=∠ABE,
∵BE平分∠ABC,∴∠ABE=∠CBE,∴∠ABE=∠AEB,∴AB=AE,∴平行四边形ABFE是菱形;
(2)①证明:过O作ON∥BC交DC于N,如图2所示:
∵AD∥BC,AB∥CD,∠ABC=90°,∴四边形ABCD是矩形,∴∠ADC=∠BCD=90°,AD∥BC,
∴AD∥ON∥BC,
∵O为BE的中点,∴N为DC的中点,ON⊥DC,∴OD=OC,∴∠ODC=∠OCD,
∵∠ADC=∠BCD=90°,∴∠ADO=∠BCO;
②解:过O作OM作BC于M,如图3所示:
∵四边形ABFE是平行四边形,AB=AE,∠ABC=90°,∴四边形ABFE是正方形,
∴EF=BF=AE=1,∠BFE=90°,∠AEB=∠AEF=45°,
∵O为BE的中点,∴OF=BE=OB,
∵OM⊥BC,∴BM=FM,∴OM是△BEF的中位线,∴OM=EF=,
∵∠EOD=15°,∴∠ADO=∠AEB﹣∠EOD=45°﹣15°=30°,
由(2)得:∠BCO=∠ADO=30°,∴OC=2OM=1.
27、如图,在平行四边形中,的平分线交于点,交的延长线于,以、为邻边作平行四边形.
(1)证明平行四边形是菱形;
(2)若,连结、、,
①求证:;
②求的度数;
(3)若,,,是的中点,求的长.
【解析】(1)证明:平分,,
四边形是平行四边形,,,
,,,,
又四边形是平行四边形,四边形为菱形;
(2)①四边形是平行四边形,,,,
,,
由(1)知,四边形是菱形,,,
,,
,,
是的平分线,,
,,,
,,;
②,,,,
,是等边三角形,,,
,是等边三角形,;
(3)如图2中,连接,,
,四边形是平行四边形,四边形是矩形,
又由(1)可知四边形为菱形,,四边形为正方形.
,,
为中点,,,
在和中,,,
,.
,是等腰直角三角形.
,,,.
