20.1.2中位数和众数-2020-2021学年人教版八年级数学下册专题复习提升训练(Word版含解析)
文档属性
| 名称 | 20.1.2中位数和众数-2020-2021学年人教版八年级数学下册专题复习提升训练(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 826.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 08:12:15 | ||
图片预览


文档简介
专题复习提升训练卷20.1.2中位数和众数-20-21人教版八年级数学下册
一、选择题
1、一组数据:5,8,6,3,4的中位数是( )
A.5 B.6 C.4 D.8
2、已知一组数据:9,9,9,11,7,8,6,5,则这组数据的中位数是( )
A.9 B.8 C.7 D.8.5
3、某青年球队名队员年龄情况如下:,,,,,,,,,.则这名队员年龄的众数、中位数分别是( )
A., B., C., D.,
4、已知一组数据3、8、5、、4的众数为5,则该组数据的平均数为( )
A.4 B.4.2 C.5 D.5.2
5、在一次中学生田径运动会上,参加男子跳高的21名运动员的成绩如下表所示:
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 5 4 4 3
则这些运动员成绩的中位数、众数分别为( )
A.1.65 m,1.70 m B.1.65 m,1.65 m
C.1.70 m,1.65 m D.1.70 m,1.70 m
6、某校八年级有11名同学参加数学竞赛,预赛成绩各不相同,要取前5名参加决赛.小兰已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这11名同学成绩的()
A.中位数 B.众数 C.平均数 D.不能确定
7、一次数学测试,某小组5名同学的成绩统计如下:
组员 甲 乙 丙 丁 戊 平均成绩 中位数
得分 81 77 ■ 80 82 80 ■
则被遮盖的两个数据依次是( )
A.80,80 B.81,80 C.80,2 D.81,2
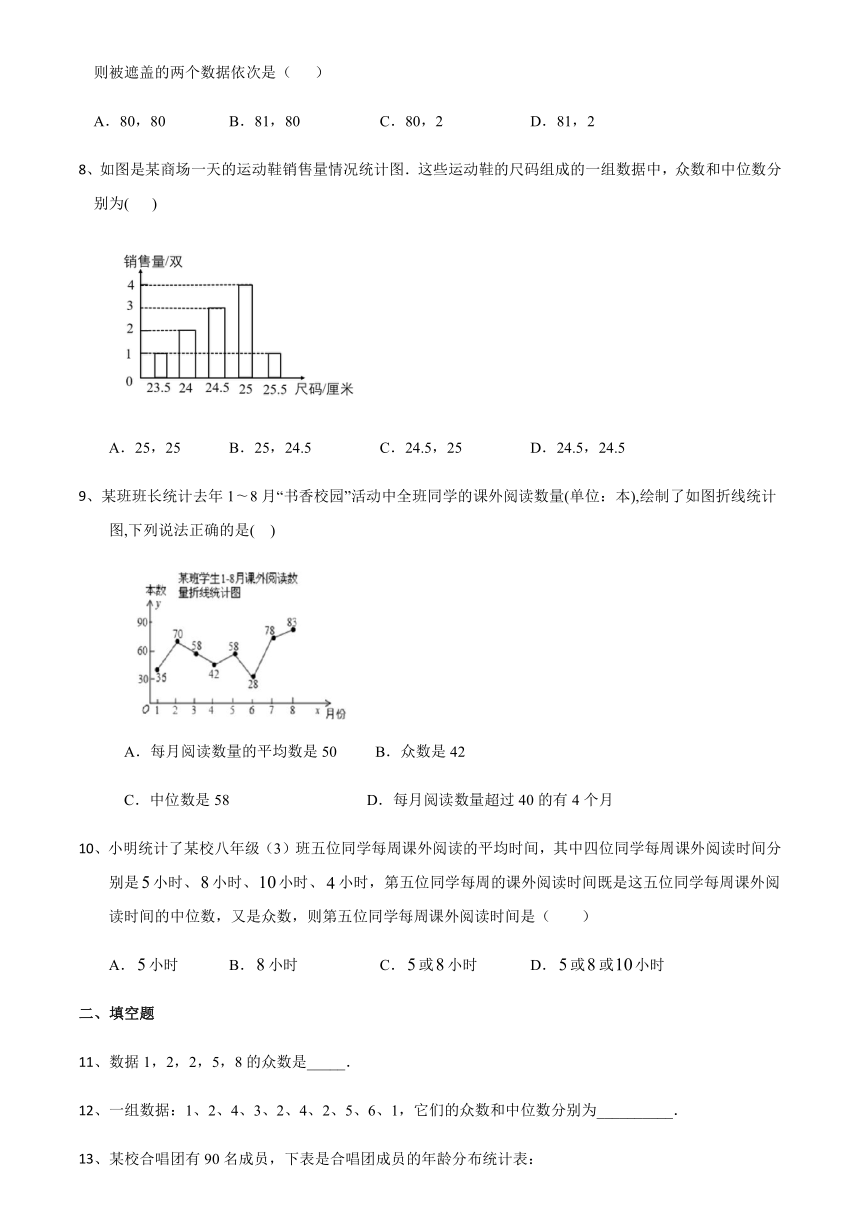
8、如图是某商场一天的运动鞋销售量情况统计图.这些运动鞋的尺码组成的一组数据中,众数和中位数分别为( )
A.25,25 B.25,24.5 C.24.5,25 D.24.5,24.5
9、某班班长统计去年1?8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
A.每月阅读数量的平均数是50 B.众数是42
C.中位数是58 D.每月阅读数量超过40的有4个月
10、小明统计了某校八年级(3)班五位同学每周课外阅读的平均时间,其中四位同学每周课外阅读时间分别是小时、小时、小时、小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是( )
A.小时 B.小时 C.或小时 D.或或小时
二、填空题
11、数据1,2,2,5,8的众数是_____.
12、一组数据:1、2、4、3、2、4、2、5、6、1,它们的众数和中位数分别为__________.
13、某校合唱团有90名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁) 13 14 15 16 17
频数(单位:名) 17 28
18
其中,队员年龄的众数是________、中位数是________.
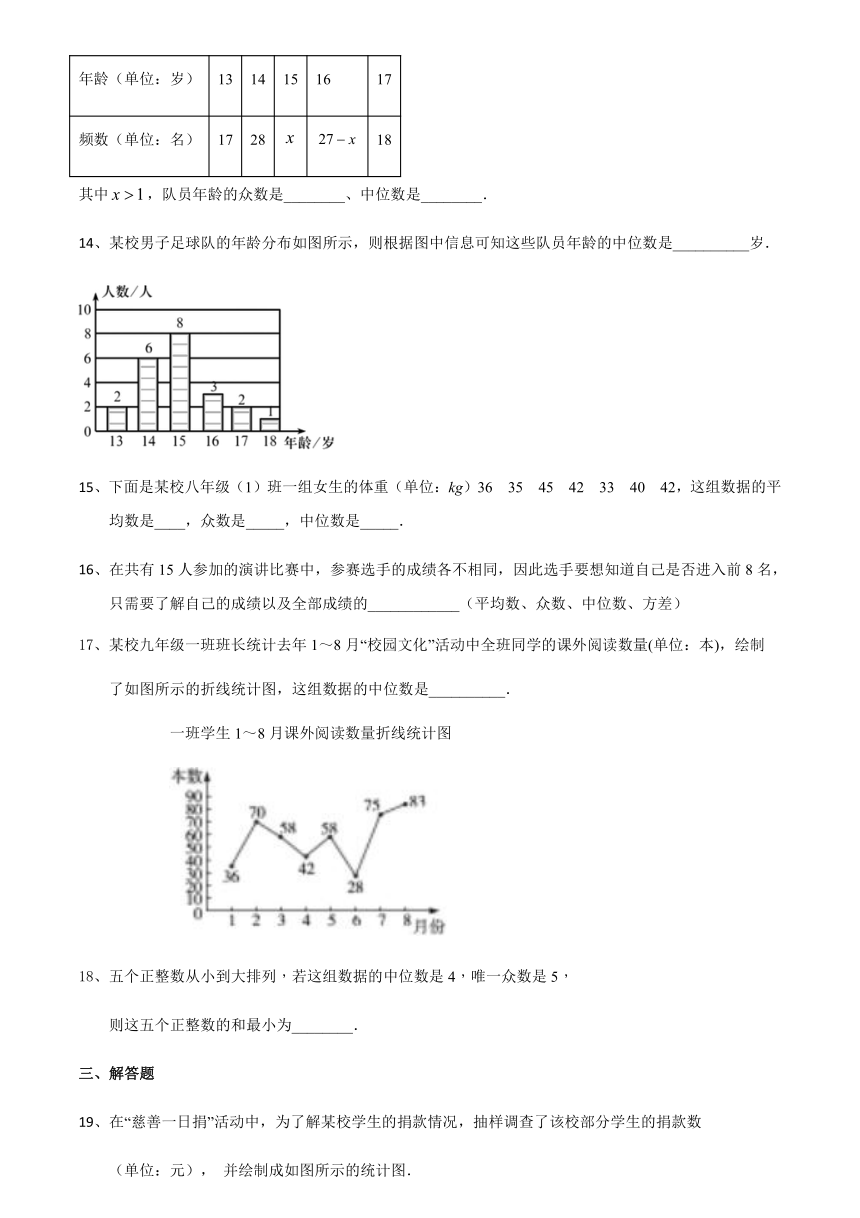
14、某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的中位数是__________岁.
15、下面是某校八年级(1)班一组女生的体重(单位:kg)36 35 45 42 33 40 42,这组数据的平均数是____,众数是_____,中位数是_____.
16、在共有15人参加的演讲比赛中,参赛选手的成绩各不相同,因此选手要想知道自己是否进入前8名,只需要了解自己的成绩以及全部成绩的____________(平均数、众数、中位数、方差)
17、某校九年级一班班长统计去年1~8月“校园文化”活动中全班同学的课外阅读数量(单位:本),绘制
了如图所示的折线统计图,这组数据的中位数是__________.
一班学生1~8月课外阅读数量折线统计图
18、五个正整数从小到大排列,若这组数据的中位数是4,唯一众数是5,
则这五个正整数的和最小为________.
三、解答题
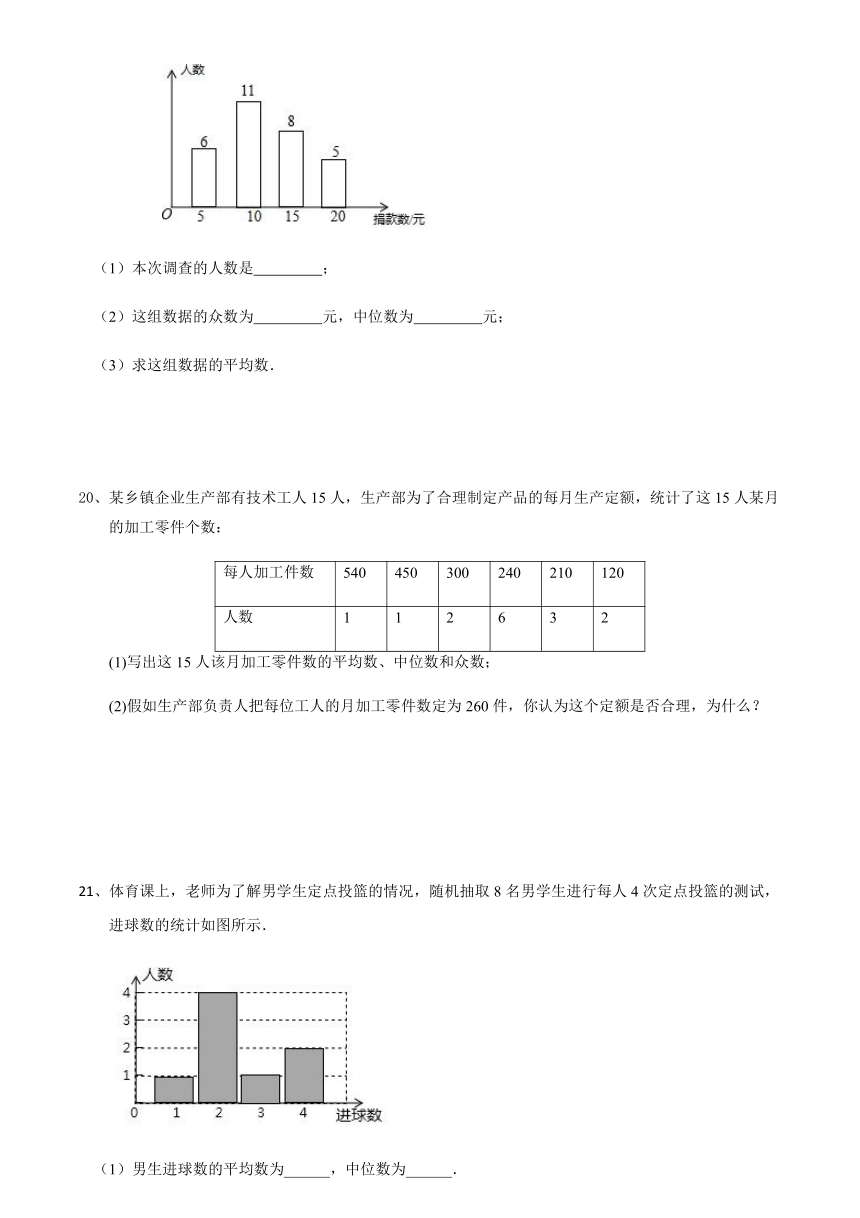
19、在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数
(单位:元), 并绘制成如图所示的统计图.
(1)本次调查的人数是 ;
(2)这组数据的众数为 元,中位数为 元;
(3)求这组数据的平均数.
20、某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工件数 540 450 300 240 210 120
人数 1 1 2 6 3 2
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假如生产部负责人把每位工人的月加工零件数定为260件,你认为这个定额是否合理,为什么?
21、体育课上,老师为了解男学生定点投篮的情况,随机抽取8名男学生进行每人4次定点投篮的测试,进球数的统计如图所示.
(1)男生进球数的平均数为______,中位数为______.
(2)投球4次,进球3个以上(含3个)为优秀,全校有男生1200人,估计为“优秀”等级的男生约为多少人?
22、在开展“好书伴我成长”读书活动中,某中学为了解八年级名学生的读书情况,随机调查了八年
级名学生读书的册数,统计数据如下表所示.
册数
人数
(1)求这个数据的平均数、众数和中位数.
(2)根据这组数据,估计该校八年级名学生在本次活动中读书多于册的人数.
23、某公司销售部有销售人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下.
销售的件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位销售人员该月销售量的平均数、中位数和众数;
(2)假设销售部负责人把每位销售人员的月销售定额定为320件,你认为是否合理,为什么?如果不合理,请你制定一个较合理的销售定额,并说明理由.
24、某山区中学280名学生参加植树节活动,要求每人植3至6棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
(1)这次调查一共抽查了______名学生的植树量;请将条形图补充完整;
(2)被调查学生每人植树量的众数是______棵、中位数是______棵;
(3)求被调查学生每人植树量的平均数,并估计这280名学生共植树多少棵?
25、钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下.
收集数据:
甲小区:85,80,95,100,90,95,85,65,75,85,90,90,70,90,100,80,80,90,95,75;
乙小区:80,60,80,95,65,100,90,85,85,80,95,75,80,90,70,80,95,75,100,90.
整理数据:
成绩x/分
甲小区 2 5 a b
乙小区 3 7 5 5
分析数据:
统计量 平均数 中位数 众数
甲小区 85.75 87.5 c
乙小区 83.5 d 80
应用数据:
(1)填空:________,__________,________,__________;
(2)若甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;
(3)社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由.
专题复习提升训练卷20.2中位数和众数-20-21人教版八年级数学下册(解析)
一、选择题
1、一组数据:5,8,6,3,4的中位数是( )
A.5 B.6 C.4 D.8
【答案】A
【分析】先把数据进行排序,再根据中位数的定义,即可求解.
【详解】解:∵一组数据:5,8,6,3,4,排序后为:3,4,5,6,8,
∴中位数为:5,
故选A.
2、已知一组数据:9,9,9,11,7,8,6,5,则这组数据的中位数是( )
A.9 B.8 C.7 D.8.5
【答案】D
【分析】先把数据排序,再根据中位数得定义,即可求解.
【详解】∵一组数据:9,9,9,11,7,8,6,5,排序后得5,6,7,8,9,9,9,11,
∴中位数为:(8+9)÷2=8.5,
故选D.
3、某青年球队名队员年龄情况如下:,,,,,,,,,.则这名队员年龄的众数、中位数分别是( )
A., B., C., D.,
【答案】B
【分析】将数据重新排列,再根据众数和中位数的定义求解可得.
【详解】解:将这组数据重新排列为18,18,19,19,19,19,20,20、21,22,
所以这组数据的众数为19,中位数为=19,
故选:B.
4、已知一组数据3、8、5、、4的众数为5,则该组数据的平均数为( )
A.4 B.4.2 C.5 D.5.2
【答案】C
【分析】根据众数的定义,先求出x的值,再求平均数,即可.
【详解】∵一组数据3、8、5、、4的众数为5,∴x=5,
∴该组数据的平均数=,
故选C.
5、在一次中学生田径运动会上,参加男子跳高的21名运动员的成绩如下表所示:
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 5 4 4 3
则这些运动员成绩的中位数、众数分别为( )
A.1.65 m,1.70 m B.1.65 m,1.65 m
C.1.70 m,1.65 m D.1.70 m,1.70 m
【答案】C
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
【详解】解:共21名学生,中位数落在第11名学生处,第11名学生的跳高成绩为1.70m,故中位数为1.70;
跳高成绩为1.65m的人数最多,故跳高成绩的众数为1.65;
故选:C.
6、某校八年级有11名同学参加数学竞赛,预赛成绩各不相同,要取前5名参加决赛.小兰已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这11名同学成绩的()
A.中位数 B.众数 C.平均数 D.不能确定
【答案】A
【分析】11人成绩的中位数是第6名的成绩.参赛选手要想知道自己是否能进入前5名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
【详解】解:由于总共有11个人,且他们的分数互不相同,第6名的成绩是中位数,要判断是否进入前5名,故应知道自己的成绩和中位数.
故选:A.
7、一次数学测试,某小组5名同学的成绩统计如下:
组员 甲 乙 丙 丁 戊 平均成绩 中位数
得分 81 77 ■ 80 82 80 ■
则被遮盖的两个数据依次是( )
A.80,80 B.81,80 C.80,2 D.81,2
【答案】A
【分析】根据平均数的计算公式先求出丙的得分,再根据中位数的意义进行分析即可得出答案.
【详解】解:根据题意得:80×5-(81+77+80+82)=80(分),则丙的得分是80分;
这组数从小到大排列:77、80、80、81、82, 则中位数是80,
故选:A
8、如图是某商场一天的运动鞋销售量情况统计图.这些运动鞋的尺码组成的一组数据中,众数和中位数分别为( )
A.25,25 B.25,24.5 C.24.5,25 D.24.5,24.5
【答案】B
【分析】先从统计图中得到数据,然后根据众数和中位数的定义判断.
【详解】从小到大排列此数据为:23.5、24、24、24.5、24.5、24.5、25、25、25、25,25.5,
数据25出现了4次最多为众数,
共11个数,中间的数是24.5,
∴24.5为中位数.
所以本题这组数据的众数是25,中位数是24.5.
故选:B.
9、某班班长统计去年1?8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
A.每月阅读数量的平均数是50 B.众数是42
C.中位数是58 D.每月阅读数量超过40的有4个月
【答案】C
【分析】根据平均数的计算方法,可判断A;根据众数的定义,可判断B;根据中位数的定义,可判断C;根据折线统计图中的数据,可判断D.
【详解】A. 每月阅读数量的平均数是 =53,故A错误;
B. 出现次数最多的是58,众数是58,故B错误;
C. 由小到大顺序排列数据28,36,42,58,58,70,78,83,中位数是=58,故C正确;
D. 由折线统计图看出每月阅读量超过40天的有6个月,故D错误;
故选C.
10、小明统计了某校八年级(3)班五位同学每周课外阅读的平均时间,其中四位同学每周课外阅读时间分别是小时、小时、小时、小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是( )
A.小时 B.小时 C.或小时 D.或或小时
【答案】C
【分析】利用众数及中位数的定义解答即可.
【详解】解:当第五位同学的课外阅读时间为4小时时,此时五个数据为4,4,5,8,10,众数为4,中位数为5,不合题意;
当第五位同学的课外阅读时间为5小时时,此时五个数据为4,5,5,8,10,众数为5,中位数为5,符合题意;
当第五位同学的课外阅读时间为8小时时,此时五个数据为4,5,8,8,10,众数为8,中位数为8,符合题意;
当第五位同学的课外阅读时间为10小时时,此时五个数据为4,5,8,10,10,众数为10,中位数为8,不合题意;故第五位同学的每周课外阅读时间为5或8小时.
故答案为C.
二、填空题
11、数据1,2,2,5,8的众数是_____.
【答案】2
【分析】众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
【详解】解:在这一组数据中2是出现次数最多的,故众数是2.
故答案为:2.
12、一组数据:1、2、4、3、2、4、2、5、6、1,它们的众数和中位数分别为__________.
【答案】2;2.5
【分析】根据众数和中位数的定义,即可确定结论;
【详解】解:这组数据从小到大排列为:1、1、2、2、2、3、4、4、5、6,
∴这组数据的众数是2,
中位数为:
故答案为:2;2.5
13、某校合唱团有90名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁) 13 14 15 16 17
频数(单位:名) 17 28
18
其中,队员年龄的众数是________、中位数是________.
【答案】14岁 14.5岁
【分析】由频数分布表可知年龄15岁和年龄16岁的两组的频数和为27,即可得知总人数,结合前两组的频数知出现次数最多的数据及第45、46个数据的平均数,可得答案.
【详解】解:由表可知,年龄为15岁与年龄为16岁的频数和为x+27-x=27,
则总人数为:17+28+27+18=90,
故该组数据的众数为14岁,
中位数为:(14+15)÷2=14.5(岁).
故答案为:14岁,14.5岁.
14、某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的中位数是__________岁.
【答案】
【分析】由图得到男子足球队的年龄及对应的人数,再根据中位数的概念即可得答案.
【详解】由图可知:13岁的有2人,14岁的有6人,15岁的有8人,16岁的有3人,
17岁的有2人,18岁的有1人,
∵足球队共有队员2+6+8+3+2+1=22人,
∴中位数是11名和第12名的平均年龄,
∵把这组数据从小到大排列11名和第12名的年龄分别是15岁、15岁,
∴这些队员年龄的中位数是15岁,
故答案为:15
15、下面是某校八年级(1)班一组女生的体重(单位:kg)36 35 45 42 33 40 42,这组数据的平均数是____,众数是_____,中位数是_____.
【答案】
【分析】分别利用平均数、众数及中位数的定义求解后即可得出答案.
【详解】解:将数据重新排列为33、35、36、40、42、42、45,
所以这组数据的平均数为,
众数为、中位数为,
故答案为:、、.
16、在共有15人参加的演讲比赛中,参赛选手的成绩各不相同,因此选手要想知道自己是否进入前8名,只需要了解自己的成绩以及全部成绩的____________(平均数、众数、中位数、方差)
【答案】中位数
【分析】此题是中位数在生活中的运用,知道自己的成绩以及全部成绩的中位数就可知道自己是否进入前8名.
【详解】15名参赛选手的成绩各不相同,第8名的成绩就是这组数据的中位数
所以选手知道自己的成绩和中位数就可知道自己是否进入前8名.而平均数、众数及方差并不能准确反映该选手能否进入前8名.
故答案为:中位数.
17、某校九年级一班班长统计去年1~8月“校园文化”活动中全班同学的课外阅读数量(单位:本),绘制
了如图所示的折线统计图,这组数据的中位数是__________.
一班学生1~8月课外阅读数量折线统计图
答案:58
18、五个正整数从小到大排列,若这组数据的中位数是4,唯一众数是5,
则这五个正整数的和最小为________.
[解析] 将这组数据按从小到大的顺序排列后,处于中间位置的那个数是中位数,众数是一组数据中出现次数最多的数.
根据题意得这组数据有两个为5,另两个为小于4且不相等的整数,所以最小的两个为1,2.
则这组数据的最小的和是1+2+4+5+5=17.故答案为17.
三、解答题
19、在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数
(单位:元), 并绘制成如图所示的统计图.
(1)本次调查的人数是 ;
(2)这组数据的众数为 元,中位数为 元;
(3)求这组数据的平均数.
【答案】(1)30;(2)10,10;(3)这组数据的平均数为12元.
【分析】(1)由各小组的频数之和可得出本次调查的人数;
(2)由众数和中位数的定义即可得出结果;
(3)由加权平均数公式即可得出结果.
【详解】解:(1)本次调查的人数是6+11+8+5=30;
故答案为:30.
(2)这组数据中出现次数最多的是元,所以这组数据的众数为10元,
这组数据是按从小到大的顺序排列的,第个数据分别是,所以这组数据的中位数为
元;
故答案为:10,10.
(3)这组数据的平均数为(元)
答:这组数据的平均数为12元.
20、某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工件数 540 450 300 240 210 120
人数 1 1 2 6 3 2
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假如生产部负责人把每位工人的月加工零件数定为260件,你认为这个定额是否合理,为什么?
解:(1)平均数:260(件),中位数:240(件),众数:240(件).
(2)不合理.因为表中数据显示,每月能完成260件的人数一共是4人,还有11人不能达到此定额,尽管260是平均数,但不利于调动多数员工的积极性.因为240既是中位数,又是众数,是大多数人能达到的定额,故定额为240较为合理.
21、体育课上,老师为了解男学生定点投篮的情况,随机抽取8名男学生进行每人4次定点投篮的测试,进球数的统计如图所示.
(1)男生进球数的平均数为______,中位数为______.
(2)投球4次,进球3个以上(含3个)为优秀,全校有男生1200人,估计为“优秀”等级的男生约为多少人?
【答案】(1)2.5,2;(2)估计为“优秀”等级的男生约为450人.
【分析】(1)根据平均数、中位数的定义进行计算即可;
(2)先算出样本的优秀率,再估计总体的优秀人数.
【详解】解:(1)男生进球数的平均数:,
男生进球数的中位数;按投球个数排序1,2,2,2,2,3,4,4,第4与第5两个数据都
是2,中位数为2,
故答案为:2.5,2;
(2)优秀率:(人),
答:全校有男生人,估计为“优秀”等级的男生约为人.
22、在开展“好书伴我成长”读书活动中,某中学为了解八年级名学生的读书情况,随机调查了八年
级名学生读书的册数,统计数据如下表所示.
册数
人数
(1)求这个数据的平均数、众数和中位数.
(2)根据这组数据,估计该校八年级名学生在本次活动中读书多于册的人数.
【答案】(1)平均数为2;众数为3;中位数为2;(2)216人.
【分析】(1)根据平均数、众数、中位数的概念求解;
(2)根据样本数据,估计本次活动中读书多于2册的人数.
【详解】解:(1)由题意得,平均数为:,
读书册数为3的人数最多,即众数为3,
第25人和第26人读数厕所的平均值为中位数,及中位数为:,
(2)(人.
答:估计七年级读书多于2册的有216人.
23、某公司销售部有销售人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下.
销售的件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位销售人员该月销售量的平均数、中位数和众数;
(2)假设销售部负责人把每位销售人员的月销售定额定为320件,你认为是否合理,为什么?如果不合理,请你制定一个较合理的销售定额,并说明理由.
解:(1)平均数是
=320(件),
表中的数据是按从大到小的顺序排列的,处于中间位置的是210,因而中位数是210件,
210出现了5次,出现的次数最多,所以众数是210件.
(2)不合理.
因为15人中有13人的销售额不到320件,320件虽是所给这组数据的平均数,它却不能很好地反映销售人员的一般水平.销售定额定为210件合适些.因为210件既是中位数,又是众数,是大部分人能达到的定额.
24、某山区中学280名学生参加植树节活动,要求每人植3至6棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
(1)这次调查一共抽查了______名学生的植树量;请将条形图补充完整;
(2)被调查学生每人植树量的众数是______棵、中位数是______棵;
(3)求被调查学生每人植树量的平均数,并估计这280名学生共植树多少棵?
【答案】(1)20,见解析;(2)4;4;(3)平均数为5.3棵,这280名学生共植树1848棵
【分析】(1)由B类型的人数及其所占百分比可得总人数,总人数乘以D类型的对应的百分比即可求出其人数,据此可补全图形;
(2)根据众数和中位数的概念可得答案;
(3)先求出样本的平均数,再乘以总人数即可.
【详解】解:(1)这次调查一共抽查植树的学生人数为8÷40%=20(人),
D类人数=20×10%=2(人);
条形图补充如图:
故答案为:20;
(2)植树4棵的人数最多,则众数是4,
共有20人植树,其中位数是第10、11人植树数量的平均数,则中位数是4,
故答案为:4、4;
(3)(棵),
5.3×280=1484(棵).
答:估计这3280名学生共植树1484棵.
25、钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下.
收集数据:
甲小区:85,80,95,100,90,95,85,65,75,85,90,90,70,90,100,80,80,90,95,75;
乙小区:80,60,80,95,65,100,90,85,85,80,95,75,80,90,70,80,95,75,100,90.
整理数据:
成绩x/分
甲小区 2 5 a b
乙小区 3 7 5 5
分析数据:
统计量 平均数 中位数 众数
甲小区 85.75 87.5 c
乙小区 83.5 d 80
应用数据:
(1)填空:________,__________,________,__________;
(2)若甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;
(3)社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由.
【答案】(1)8,5 ,90 ,82.5;(2)200;(3)见解析.
【分析】(1)由数据及表格可直接进行求解;
(2)由题意易得甲小区成绩大于90分的人所占比为,进而问题可求解;
(3)根据平均数、中位数及众数可直接进行求解.
【详解】解:(1)由题意得:
甲小区成绩在之间的人数有8人,在的人数为5人,
乙小区成绩从小到大排列为:60,65,70,75,75,80,80,80,80,80,85,85,90,90,90,95,95,95,100,100,则中位数为82.5,
甲小区的众数为90,
∴8,,,,
故答案为8,5,90,82.5 ;
(2)由题意得:(人),
答:估计甲小区成绩大于90分的人数是200.
(3)由(1)及表格可得:甲小区的平均数、中位数、众数都比乙小区的大.
一、选择题
1、一组数据:5,8,6,3,4的中位数是( )
A.5 B.6 C.4 D.8
2、已知一组数据:9,9,9,11,7,8,6,5,则这组数据的中位数是( )
A.9 B.8 C.7 D.8.5
3、某青年球队名队员年龄情况如下:,,,,,,,,,.则这名队员年龄的众数、中位数分别是( )
A., B., C., D.,
4、已知一组数据3、8、5、、4的众数为5,则该组数据的平均数为( )
A.4 B.4.2 C.5 D.5.2
5、在一次中学生田径运动会上,参加男子跳高的21名运动员的成绩如下表所示:
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 5 4 4 3
则这些运动员成绩的中位数、众数分别为( )
A.1.65 m,1.70 m B.1.65 m,1.65 m
C.1.70 m,1.65 m D.1.70 m,1.70 m
6、某校八年级有11名同学参加数学竞赛,预赛成绩各不相同,要取前5名参加决赛.小兰已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这11名同学成绩的()
A.中位数 B.众数 C.平均数 D.不能确定
7、一次数学测试,某小组5名同学的成绩统计如下:
组员 甲 乙 丙 丁 戊 平均成绩 中位数
得分 81 77 ■ 80 82 80 ■
则被遮盖的两个数据依次是( )
A.80,80 B.81,80 C.80,2 D.81,2
8、如图是某商场一天的运动鞋销售量情况统计图.这些运动鞋的尺码组成的一组数据中,众数和中位数分别为( )
A.25,25 B.25,24.5 C.24.5,25 D.24.5,24.5
9、某班班长统计去年1?8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
A.每月阅读数量的平均数是50 B.众数是42
C.中位数是58 D.每月阅读数量超过40的有4个月
10、小明统计了某校八年级(3)班五位同学每周课外阅读的平均时间,其中四位同学每周课外阅读时间分别是小时、小时、小时、小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是( )
A.小时 B.小时 C.或小时 D.或或小时
二、填空题
11、数据1,2,2,5,8的众数是_____.
12、一组数据:1、2、4、3、2、4、2、5、6、1,它们的众数和中位数分别为__________.
13、某校合唱团有90名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁) 13 14 15 16 17
频数(单位:名) 17 28
18
其中,队员年龄的众数是________、中位数是________.
14、某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的中位数是__________岁.
15、下面是某校八年级(1)班一组女生的体重(单位:kg)36 35 45 42 33 40 42,这组数据的平均数是____,众数是_____,中位数是_____.
16、在共有15人参加的演讲比赛中,参赛选手的成绩各不相同,因此选手要想知道自己是否进入前8名,只需要了解自己的成绩以及全部成绩的____________(平均数、众数、中位数、方差)
17、某校九年级一班班长统计去年1~8月“校园文化”活动中全班同学的课外阅读数量(单位:本),绘制
了如图所示的折线统计图,这组数据的中位数是__________.
一班学生1~8月课外阅读数量折线统计图
18、五个正整数从小到大排列,若这组数据的中位数是4,唯一众数是5,
则这五个正整数的和最小为________.
三、解答题
19、在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数
(单位:元), 并绘制成如图所示的统计图.
(1)本次调查的人数是 ;
(2)这组数据的众数为 元,中位数为 元;
(3)求这组数据的平均数.
20、某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工件数 540 450 300 240 210 120
人数 1 1 2 6 3 2
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假如生产部负责人把每位工人的月加工零件数定为260件,你认为这个定额是否合理,为什么?
21、体育课上,老师为了解男学生定点投篮的情况,随机抽取8名男学生进行每人4次定点投篮的测试,进球数的统计如图所示.
(1)男生进球数的平均数为______,中位数为______.
(2)投球4次,进球3个以上(含3个)为优秀,全校有男生1200人,估计为“优秀”等级的男生约为多少人?
22、在开展“好书伴我成长”读书活动中,某中学为了解八年级名学生的读书情况,随机调查了八年
级名学生读书的册数,统计数据如下表所示.
册数
人数
(1)求这个数据的平均数、众数和中位数.
(2)根据这组数据,估计该校八年级名学生在本次活动中读书多于册的人数.
23、某公司销售部有销售人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下.
销售的件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位销售人员该月销售量的平均数、中位数和众数;
(2)假设销售部负责人把每位销售人员的月销售定额定为320件,你认为是否合理,为什么?如果不合理,请你制定一个较合理的销售定额,并说明理由.
24、某山区中学280名学生参加植树节活动,要求每人植3至6棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
(1)这次调查一共抽查了______名学生的植树量;请将条形图补充完整;
(2)被调查学生每人植树量的众数是______棵、中位数是______棵;
(3)求被调查学生每人植树量的平均数,并估计这280名学生共植树多少棵?
25、钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下.
收集数据:
甲小区:85,80,95,100,90,95,85,65,75,85,90,90,70,90,100,80,80,90,95,75;
乙小区:80,60,80,95,65,100,90,85,85,80,95,75,80,90,70,80,95,75,100,90.
整理数据:
成绩x/分
甲小区 2 5 a b
乙小区 3 7 5 5
分析数据:
统计量 平均数 中位数 众数
甲小区 85.75 87.5 c
乙小区 83.5 d 80
应用数据:
(1)填空:________,__________,________,__________;
(2)若甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;
(3)社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由.
专题复习提升训练卷20.2中位数和众数-20-21人教版八年级数学下册(解析)
一、选择题
1、一组数据:5,8,6,3,4的中位数是( )
A.5 B.6 C.4 D.8
【答案】A
【分析】先把数据进行排序,再根据中位数的定义,即可求解.
【详解】解:∵一组数据:5,8,6,3,4,排序后为:3,4,5,6,8,
∴中位数为:5,
故选A.
2、已知一组数据:9,9,9,11,7,8,6,5,则这组数据的中位数是( )
A.9 B.8 C.7 D.8.5
【答案】D
【分析】先把数据排序,再根据中位数得定义,即可求解.
【详解】∵一组数据:9,9,9,11,7,8,6,5,排序后得5,6,7,8,9,9,9,11,
∴中位数为:(8+9)÷2=8.5,
故选D.
3、某青年球队名队员年龄情况如下:,,,,,,,,,.则这名队员年龄的众数、中位数分别是( )
A., B., C., D.,
【答案】B
【分析】将数据重新排列,再根据众数和中位数的定义求解可得.
【详解】解:将这组数据重新排列为18,18,19,19,19,19,20,20、21,22,
所以这组数据的众数为19,中位数为=19,
故选:B.
4、已知一组数据3、8、5、、4的众数为5,则该组数据的平均数为( )
A.4 B.4.2 C.5 D.5.2
【答案】C
【分析】根据众数的定义,先求出x的值,再求平均数,即可.
【详解】∵一组数据3、8、5、、4的众数为5,∴x=5,
∴该组数据的平均数=,
故选C.
5、在一次中学生田径运动会上,参加男子跳高的21名运动员的成绩如下表所示:
成绩/m 1.50 1.60 1.65 1.70 1.75 1.80
人数 2 3 5 4 4 3
则这些运动员成绩的中位数、众数分别为( )
A.1.65 m,1.70 m B.1.65 m,1.65 m
C.1.70 m,1.65 m D.1.70 m,1.70 m
【答案】C
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
【详解】解:共21名学生,中位数落在第11名学生处,第11名学生的跳高成绩为1.70m,故中位数为1.70;
跳高成绩为1.65m的人数最多,故跳高成绩的众数为1.65;
故选:C.
6、某校八年级有11名同学参加数学竞赛,预赛成绩各不相同,要取前5名参加决赛.小兰已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这11名同学成绩的()
A.中位数 B.众数 C.平均数 D.不能确定
【答案】A
【分析】11人成绩的中位数是第6名的成绩.参赛选手要想知道自己是否能进入前5名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
【详解】解:由于总共有11个人,且他们的分数互不相同,第6名的成绩是中位数,要判断是否进入前5名,故应知道自己的成绩和中位数.
故选:A.
7、一次数学测试,某小组5名同学的成绩统计如下:
组员 甲 乙 丙 丁 戊 平均成绩 中位数
得分 81 77 ■ 80 82 80 ■
则被遮盖的两个数据依次是( )
A.80,80 B.81,80 C.80,2 D.81,2
【答案】A
【分析】根据平均数的计算公式先求出丙的得分,再根据中位数的意义进行分析即可得出答案.
【详解】解:根据题意得:80×5-(81+77+80+82)=80(分),则丙的得分是80分;
这组数从小到大排列:77、80、80、81、82, 则中位数是80,
故选:A
8、如图是某商场一天的运动鞋销售量情况统计图.这些运动鞋的尺码组成的一组数据中,众数和中位数分别为( )
A.25,25 B.25,24.5 C.24.5,25 D.24.5,24.5
【答案】B
【分析】先从统计图中得到数据,然后根据众数和中位数的定义判断.
【详解】从小到大排列此数据为:23.5、24、24、24.5、24.5、24.5、25、25、25、25,25.5,
数据25出现了4次最多为众数,
共11个数,中间的数是24.5,
∴24.5为中位数.
所以本题这组数据的众数是25,中位数是24.5.
故选:B.
9、某班班长统计去年1?8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
A.每月阅读数量的平均数是50 B.众数是42
C.中位数是58 D.每月阅读数量超过40的有4个月
【答案】C
【分析】根据平均数的计算方法,可判断A;根据众数的定义,可判断B;根据中位数的定义,可判断C;根据折线统计图中的数据,可判断D.
【详解】A. 每月阅读数量的平均数是 =53,故A错误;
B. 出现次数最多的是58,众数是58,故B错误;
C. 由小到大顺序排列数据28,36,42,58,58,70,78,83,中位数是=58,故C正确;
D. 由折线统计图看出每月阅读量超过40天的有6个月,故D错误;
故选C.
10、小明统计了某校八年级(3)班五位同学每周课外阅读的平均时间,其中四位同学每周课外阅读时间分别是小时、小时、小时、小时,第五位同学每周的课外阅读时间既是这五位同学每周课外阅读时间的中位数,又是众数,则第五位同学每周课外阅读时间是( )
A.小时 B.小时 C.或小时 D.或或小时
【答案】C
【分析】利用众数及中位数的定义解答即可.
【详解】解:当第五位同学的课外阅读时间为4小时时,此时五个数据为4,4,5,8,10,众数为4,中位数为5,不合题意;
当第五位同学的课外阅读时间为5小时时,此时五个数据为4,5,5,8,10,众数为5,中位数为5,符合题意;
当第五位同学的课外阅读时间为8小时时,此时五个数据为4,5,8,8,10,众数为8,中位数为8,符合题意;
当第五位同学的课外阅读时间为10小时时,此时五个数据为4,5,8,10,10,众数为10,中位数为8,不合题意;故第五位同学的每周课外阅读时间为5或8小时.
故答案为C.
二、填空题
11、数据1,2,2,5,8的众数是_____.
【答案】2
【分析】众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
【详解】解:在这一组数据中2是出现次数最多的,故众数是2.
故答案为:2.
12、一组数据:1、2、4、3、2、4、2、5、6、1,它们的众数和中位数分别为__________.
【答案】2;2.5
【分析】根据众数和中位数的定义,即可确定结论;
【详解】解:这组数据从小到大排列为:1、1、2、2、2、3、4、4、5、6,
∴这组数据的众数是2,
中位数为:
故答案为:2;2.5
13、某校合唱团有90名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁) 13 14 15 16 17
频数(单位:名) 17 28
18
其中,队员年龄的众数是________、中位数是________.
【答案】14岁 14.5岁
【分析】由频数分布表可知年龄15岁和年龄16岁的两组的频数和为27,即可得知总人数,结合前两组的频数知出现次数最多的数据及第45、46个数据的平均数,可得答案.
【详解】解:由表可知,年龄为15岁与年龄为16岁的频数和为x+27-x=27,
则总人数为:17+28+27+18=90,
故该组数据的众数为14岁,
中位数为:(14+15)÷2=14.5(岁).
故答案为:14岁,14.5岁.
14、某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的中位数是__________岁.
【答案】
【分析】由图得到男子足球队的年龄及对应的人数,再根据中位数的概念即可得答案.
【详解】由图可知:13岁的有2人,14岁的有6人,15岁的有8人,16岁的有3人,
17岁的有2人,18岁的有1人,
∵足球队共有队员2+6+8+3+2+1=22人,
∴中位数是11名和第12名的平均年龄,
∵把这组数据从小到大排列11名和第12名的年龄分别是15岁、15岁,
∴这些队员年龄的中位数是15岁,
故答案为:15
15、下面是某校八年级(1)班一组女生的体重(单位:kg)36 35 45 42 33 40 42,这组数据的平均数是____,众数是_____,中位数是_____.
【答案】
【分析】分别利用平均数、众数及中位数的定义求解后即可得出答案.
【详解】解:将数据重新排列为33、35、36、40、42、42、45,
所以这组数据的平均数为,
众数为、中位数为,
故答案为:、、.
16、在共有15人参加的演讲比赛中,参赛选手的成绩各不相同,因此选手要想知道自己是否进入前8名,只需要了解自己的成绩以及全部成绩的____________(平均数、众数、中位数、方差)
【答案】中位数
【分析】此题是中位数在生活中的运用,知道自己的成绩以及全部成绩的中位数就可知道自己是否进入前8名.
【详解】15名参赛选手的成绩各不相同,第8名的成绩就是这组数据的中位数
所以选手知道自己的成绩和中位数就可知道自己是否进入前8名.而平均数、众数及方差并不能准确反映该选手能否进入前8名.
故答案为:中位数.
17、某校九年级一班班长统计去年1~8月“校园文化”活动中全班同学的课外阅读数量(单位:本),绘制
了如图所示的折线统计图,这组数据的中位数是__________.
一班学生1~8月课外阅读数量折线统计图
答案:58
18、五个正整数从小到大排列,若这组数据的中位数是4,唯一众数是5,
则这五个正整数的和最小为________.
[解析] 将这组数据按从小到大的顺序排列后,处于中间位置的那个数是中位数,众数是一组数据中出现次数最多的数.
根据题意得这组数据有两个为5,另两个为小于4且不相等的整数,所以最小的两个为1,2.
则这组数据的最小的和是1+2+4+5+5=17.故答案为17.
三、解答题
19、在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数
(单位:元), 并绘制成如图所示的统计图.
(1)本次调查的人数是 ;
(2)这组数据的众数为 元,中位数为 元;
(3)求这组数据的平均数.
【答案】(1)30;(2)10,10;(3)这组数据的平均数为12元.
【分析】(1)由各小组的频数之和可得出本次调查的人数;
(2)由众数和中位数的定义即可得出结果;
(3)由加权平均数公式即可得出结果.
【详解】解:(1)本次调查的人数是6+11+8+5=30;
故答案为:30.
(2)这组数据中出现次数最多的是元,所以这组数据的众数为10元,
这组数据是按从小到大的顺序排列的,第个数据分别是,所以这组数据的中位数为
元;
故答案为:10,10.
(3)这组数据的平均数为(元)
答:这组数据的平均数为12元.
20、某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工件数 540 450 300 240 210 120
人数 1 1 2 6 3 2
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假如生产部负责人把每位工人的月加工零件数定为260件,你认为这个定额是否合理,为什么?
解:(1)平均数:260(件),中位数:240(件),众数:240(件).
(2)不合理.因为表中数据显示,每月能完成260件的人数一共是4人,还有11人不能达到此定额,尽管260是平均数,但不利于调动多数员工的积极性.因为240既是中位数,又是众数,是大多数人能达到的定额,故定额为240较为合理.
21、体育课上,老师为了解男学生定点投篮的情况,随机抽取8名男学生进行每人4次定点投篮的测试,进球数的统计如图所示.
(1)男生进球数的平均数为______,中位数为______.
(2)投球4次,进球3个以上(含3个)为优秀,全校有男生1200人,估计为“优秀”等级的男生约为多少人?
【答案】(1)2.5,2;(2)估计为“优秀”等级的男生约为450人.
【分析】(1)根据平均数、中位数的定义进行计算即可;
(2)先算出样本的优秀率,再估计总体的优秀人数.
【详解】解:(1)男生进球数的平均数:,
男生进球数的中位数;按投球个数排序1,2,2,2,2,3,4,4,第4与第5两个数据都
是2,中位数为2,
故答案为:2.5,2;
(2)优秀率:(人),
答:全校有男生人,估计为“优秀”等级的男生约为人.
22、在开展“好书伴我成长”读书活动中,某中学为了解八年级名学生的读书情况,随机调查了八年
级名学生读书的册数,统计数据如下表所示.
册数
人数
(1)求这个数据的平均数、众数和中位数.
(2)根据这组数据,估计该校八年级名学生在本次活动中读书多于册的人数.
【答案】(1)平均数为2;众数为3;中位数为2;(2)216人.
【分析】(1)根据平均数、众数、中位数的概念求解;
(2)根据样本数据,估计本次活动中读书多于2册的人数.
【详解】解:(1)由题意得,平均数为:,
读书册数为3的人数最多,即众数为3,
第25人和第26人读数厕所的平均值为中位数,及中位数为:,
(2)(人.
答:估计七年级读书多于2册的有216人.
23、某公司销售部有销售人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下.
销售的件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位销售人员该月销售量的平均数、中位数和众数;
(2)假设销售部负责人把每位销售人员的月销售定额定为320件,你认为是否合理,为什么?如果不合理,请你制定一个较合理的销售定额,并说明理由.
解:(1)平均数是
=320(件),
表中的数据是按从大到小的顺序排列的,处于中间位置的是210,因而中位数是210件,
210出现了5次,出现的次数最多,所以众数是210件.
(2)不合理.
因为15人中有13人的销售额不到320件,320件虽是所给这组数据的平均数,它却不能很好地反映销售人员的一般水平.销售定额定为210件合适些.因为210件既是中位数,又是众数,是大部分人能达到的定额.
24、某山区中学280名学生参加植树节活动,要求每人植3至6棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
(1)这次调查一共抽查了______名学生的植树量;请将条形图补充完整;
(2)被调查学生每人植树量的众数是______棵、中位数是______棵;
(3)求被调查学生每人植树量的平均数,并估计这280名学生共植树多少棵?
【答案】(1)20,见解析;(2)4;4;(3)平均数为5.3棵,这280名学生共植树1848棵
【分析】(1)由B类型的人数及其所占百分比可得总人数,总人数乘以D类型的对应的百分比即可求出其人数,据此可补全图形;
(2)根据众数和中位数的概念可得答案;
(3)先求出样本的平均数,再乘以总人数即可.
【详解】解:(1)这次调查一共抽查植树的学生人数为8÷40%=20(人),
D类人数=20×10%=2(人);
条形图补充如图:
故答案为:20;
(2)植树4棵的人数最多,则众数是4,
共有20人植树,其中位数是第10、11人植树数量的平均数,则中位数是4,
故答案为:4、4;
(3)(棵),
5.3×280=1484(棵).
答:估计这3280名学生共植树1484棵.
25、钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下.
收集数据:
甲小区:85,80,95,100,90,95,85,65,75,85,90,90,70,90,100,80,80,90,95,75;
乙小区:80,60,80,95,65,100,90,85,85,80,95,75,80,90,70,80,95,75,100,90.
整理数据:
成绩x/分
甲小区 2 5 a b
乙小区 3 7 5 5
分析数据:
统计量 平均数 中位数 众数
甲小区 85.75 87.5 c
乙小区 83.5 d 80
应用数据:
(1)填空:________,__________,________,__________;
(2)若甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;
(3)社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由.
【答案】(1)8,5 ,90 ,82.5;(2)200;(3)见解析.
【分析】(1)由数据及表格可直接进行求解;
(2)由题意易得甲小区成绩大于90分的人所占比为,进而问题可求解;
(3)根据平均数、中位数及众数可直接进行求解.
【详解】解:(1)由题意得:
甲小区成绩在之间的人数有8人,在的人数为5人,
乙小区成绩从小到大排列为:60,65,70,75,75,80,80,80,80,80,85,85,90,90,90,95,95,95,100,100,则中位数为82.5,
甲小区的众数为90,
∴8,,,,
故答案为8,5,90,82.5 ;
(2)由题意得:(人),
答:估计甲小区成绩大于90分的人数是200.
(3)由(1)及表格可得:甲小区的平均数、中位数、众数都比乙小区的大.
