20.3数据的分析 单元复习(2)--2020-2021学年人教版八年级数学下册专题复习提升训练(Word版含解析)
文档属性
| 名称 | 20.3数据的分析 单元复习(2)--2020-2021学年人教版八年级数学下册专题复习提升训练(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 816.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 00:00:00 | ||
图片预览




文档简介
专题复习提升训练卷20.3《数据的分析》单元训练(2)-20-21人教版八年级数学下册
一、选择题
1、小颖八年级第一学期的数学成绩分别为:平时90分,期中86分,期末95分若按下图所显示的权重要求计算,则小颖该学期总评成绩为( )
A.88 B. C. D.93
2、8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为( )
A.76 B.75 C.74 D.73
3、我县今年4月某地6天的最高气温如下(单位℃):32,29,30,32,30,32.则这个地区最高气温的众数和中位数分别是( )
A.30,32 B.32,30 C.32,31 D.32,32
4、某商场对上周末某品牌运动服的销售情况进行了统计,如下表所示:经理决定本周进货时多进一些红色的,可用来解释这一现象的统计知识是( )
颜色 黄色 绿色 白色 紫色 红色
数量(件) 120 150 230 75 430
A.平均数 B.中位数
C.众数 D.平均数与中位数
5、在“全民读书月”活动中,小明调查了班级里40名同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图,则这40名同学购买课外书花费的众数和中位数分别为( )
A.30元,30元 B.30元,50元 C.50元,50元 D.50元,80元
6、若样本,,,,的平均数为10,方差为4,则对于样本,,,,,下列结论正确的是( )
A.平均数为10,方差为2 B.众数不变,方差为4
C.平均数为7,方差为2 D.中位数变小,方差不变
7、某班有46人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体划试.因此计算其他45人的平均分为88分,方差为38.后来小亮进行了补测,成绩为88分,关于该班46人的测试成绩,下列说法正确的是( )
A.平均分和方差都不变 B.平均分不变,方差变大
C.平均分不变,方差变小 D.平均分和方差都改变
8、在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是8环,其中甲的成绩的方差,乙的成绩的方差,则( )
A.甲比乙的成绩稳定 B.乙比甲的成绩稳定
C.甲、乙两人的成绩一样稳定 D.无法确定谁的成绩更稳定
9、甲、乙、丙、丁四位同学在五次数学测验中,他们成绩的平均分相等,方差分别是2.3、3.8、5.2、6.2,则成绩最稳定的同学是( )
A.甲 B.乙 C.丙 D.丁
10、八年级一,二班的同学在一次数学测验中的成绩统计情况如下表:
班级 参加人数 中位数 平均数 方差
一
二
某同学分析后得到如下结论:①一,二班学生成绩平均水平相同;②二班优生人数不少于一班(优生线分);③一班学生的成绩相对稳定.其中正确的是( )
A.②③ B.①② C.①③ D.①②③
二、填空题
11、如果一组数据,,,,的平均数是,那么是_____.
12、某校学生的数学期末总评成绩由平时成绩、期中成绩、期末成绩3个部分组成,各部分比例如图所示.小明这三项的成绩依次是90分,85分,92分,则小明的期末总评成绩是_____.
13、某市在一次空气污染指数抽查中,收集到7天的数据如下:60,75,70,60,56,75,60.该组数据的中位数是__,众数是__.
14、在重庆八中“青春飞扬”艺术节的钢琴演奏比赛决赛中,参加比赛的10名选手成绩统计如图所示,则这10名学生成绩的中位数是___________.
15、在预防新型冠状病毒期间,有关部门加强了对市场的监管力度.在对某药店检查中,抽检了6包口罩(每包10只),得到合格的口罩只数分别是7,10,9,10,7,8,则该组数据7,10,9,10,7,8的中位数是_____.
16、已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是1,则数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的方差是______.
17、青少年科技创新大赛是一项具有30年历史的全国性青少年科技创新成果和科学探究项目的综合性科技竞赛.某校准备从甲、乙、丙、丁四个科创小组中选出一组参加青少年科技创新大赛.表格反映的是各组平时成绩的平均数(单位:分),及方差,如果要选出一个成绩较好且状态稳定的组去参赛,那么应去的组是________.
甲 乙 丙 丁
7 8 8 7
1 1.2 0.9 1.8
18、已知一组数据x1,x2,…,xn的方差是s2,则新的一组数据ax1+1,ax2+1,…,axn+1(a为常数,a≠0)的方差是 .(用含a,s2的代数式表示)
三、解答题
19、为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在学校实习基地单位时间内现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如图表所示(单位mm):
平均数 方差 完全符合要求个数
A 20 0.026 2
B 20 SB2
根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为哪个同学的成绩好些?
(2)计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些?
(3)考虑图中折线走势,你认为派谁去参赛较合适?说明你的理由.
20、甲、乙两人在次打靶测试中命中的环数如下:
第一次 第二次 第三次 第四次 第五次
甲
乙
从数据来看,谁的成绩较稳定?请你通过计算方差说明理由.
21、一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容∶演讲能力∶演讲效果的比例计算选手的综合成绩(百分制),进入决赛的前两名选手的单项成绩如下表所示:
选手 演讲内容 演讲能力 演讲效果
85 95 95
95 85 95
22、从某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分四个等级,将调査结果绘制成如下的不完整的条形统计图和扇形统计图.根据图中信息解决下列问题.
(1)共抽取______________名学生,成绩为2分的学生有_________名
(2)求抽取的所有学生成绩的平均数.
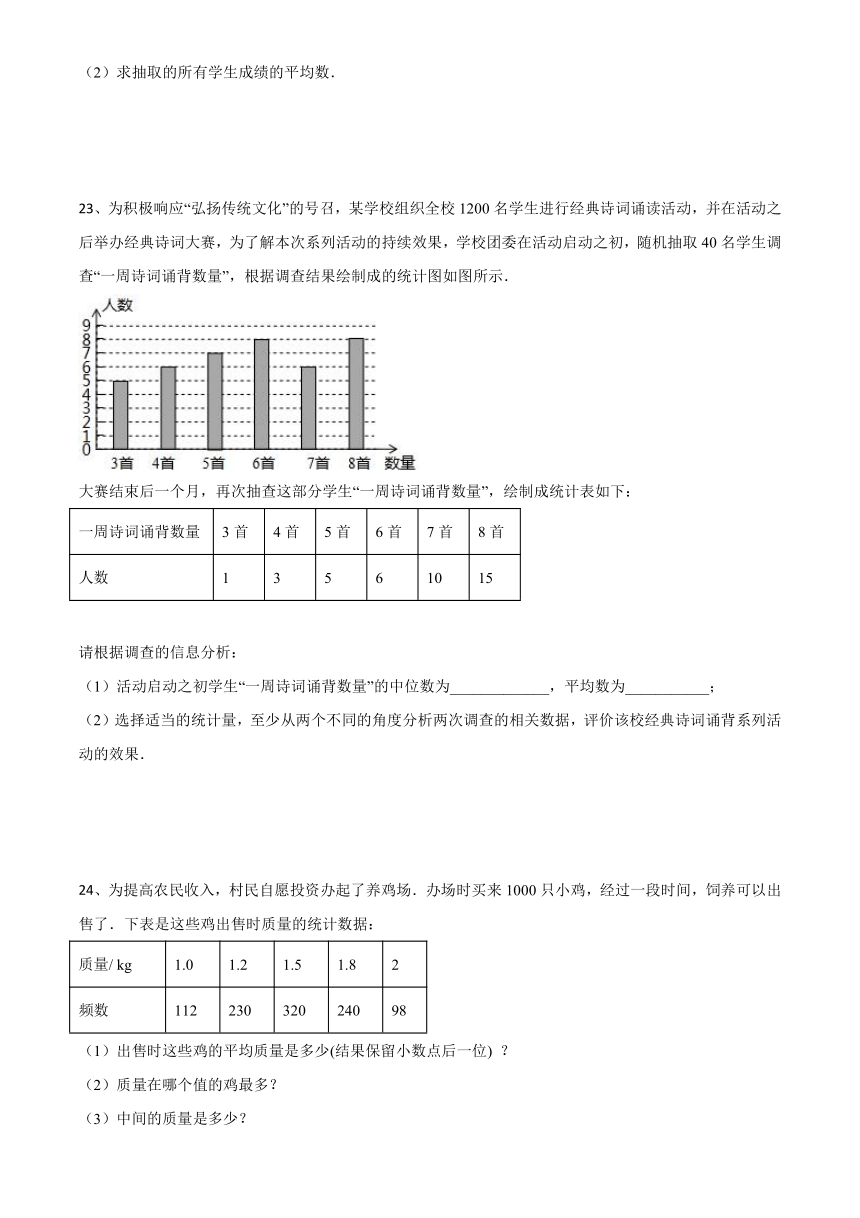
23、为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 3首 4首 5首 6首 7首 8首
人数 1 3 5 6 10 15
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为_____________,平均数为___________;
(2)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
24、为提高农民收入,村民自愿投资办起了养鸡场.办场时买来1000只小鸡,经过一段时间,饲养可以出售了.下表是这些鸡出售时质量的统计数据:
质量/ kg 1.0 1.2 1.5 1.8 2
频数 112 230 320 240 98
(1)出售时这些鸡的平均质量是多少(结果保留小数点后一位) ?
(2)质量在哪个值的鸡最多?
(3)中间的质量是多少?
25、某市举行知识大赛,A校.B校各派出5名选手组成代表队参加比赛.两校派出选手的比赛成绩如图所示.
根据以上信息.整理分析数据如表:
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
(1)a= ;b= ;
(2)填空:(填“A校”或“B校”)
①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是 ;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是 ;
③从两校比赛成绩的方差的角度来比较, 代表队选手成绩的方差较大.
专题复习提升训练卷20.4《数据的分析》单元训练(2)-20-21人教版八年级数学下册(解析)
一、选择题
1、小颖八年级第一学期的数学成绩分别为:平时90分,期中86分,期末95分若按下图所显示的权重要求计算,则小颖该学期总评成绩为( )
A.88 B. C. D.93
【答案】B
【分析】根据加权平均数的计算公式即可得.
【详解】由题意得:小颖该学期总评成绩为(分)
故选:B.
2、8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为( )
A.76 B.75 C.74 D.73
【答案】D
【分析】
根据平均数公式即可得到结果.
【详解】
由题意得,
解得
3、我县今年4月某地6天的最高气温如下(单位℃):32,29,30,32,30,32.则这个地区最高气温的众数和中位数分别是( )
A.30,32 B.32,30 C.32,31 D.32,32
【答案】C
【分析】
根据众数和中位数的定义,结合所给数据即可得出答案.
【详解】
解:将这组数据按从小到大的顺序排列为:29,30,30,32,32,32,
出现最多的数字为:32,故众数是32,
中位数为第3、4个数的平均数,即为.
故选:C.
4、某商场对上周末某品牌运动服的销售情况进行了统计,如下表所示:经理决定本周进货时多进一些红色的,可用来解释这一现象的统计知识是( )
颜色 黄色 绿色 白色 紫色 红色
数量(件) 120 150 230 75 430
A.平均数 B.中位数
C.众数 D.平均数与中位数
【答案】C
【分析】
商场经理最值得关注的应该是爱买哪种颜色运动服的人数最多,即众数.
【详解】
解:由于销售最多的颜色为红色,且远远多于其他颜色,所以选择多进红色运动服的主要根据众数.
故选:C
5、在“全民读书月”活动中,小明调查了班级里40名同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图,则这40名同学购买课外书花费的众数和中位数分别为( )
A.30元,30元 B.30元,50元 C.50元,50元 D.50元,80元
【答案】B
【分析】
众数就是出现次数最多的数,据此即可判断;中位数就是数据从小到大排列后,处于中间位置的数或中间两数的平均数,根据定义判断即可.
【详解】
解:∵购买课外书花费30元的有12人,人数最多,
∴众数是30元;
把这些数从小到大排列,最中间的两个数是第20和第21个数,都是50元,
则中位数是(元);
故选:B.
6、若样本,,,,的平均数为10,方差为4,则对于样本,,,,,下列结论正确的是( )
A.平均数为10,方差为2 B.众数不变,方差为4
C.平均数为7,方差为2 D.中位数变小,方差不变
【答案】D
【分析】
利用平均数、中位数、众数和方差的意义进行判断.
【详解】
解:∵样本x1,x2,x3,…,xn的平均数为10,方差为4,
∴样本x1﹣3,x2﹣3,x3﹣3,…,xn﹣3
的平均数为 =7,
原众数和中位数减小了3,方差为各数据偏离平均数的平方,各数都减小了3,平均数也减小了3,但偏离平均数的程度不变,故方差不变.
故选:D.
7、某班有46人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体划试.因此计算其他45人的平均分为88分,方差为38.后来小亮进行了补测,成绩为88分,关于该班46人的测试成绩,下列说法正确的是( )
A.平均分和方差都不变 B.平均分不变,方差变大
C.平均分不变,方差变小 D.平均分和方差都改变
【答案】C
【分析】
根据平均数,方差的定义计算即可.
【详解】
解:∵小亮的成绩和其他45人的平均数相同,都是88分,
该班46人的平均分为:(分),
该班46人的方差为:,
∴该班46人的测试成绩的平均分不变,方差变小,
故选:C.
8、在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是8环,其中甲的成绩的方差,乙的成绩的方差,则( )
A.甲比乙的成绩稳定 B.乙比甲的成绩稳定
C.甲、乙两人的成绩一样稳定 D.无法确定谁的成绩更稳定
【答案】A
【分析】
根据方差的定义,方差越小数据越稳定.
【详解】
解:∵两人的平均成绩相同,S甲2=0.3<S乙2=2.1,方差小的为甲,
∴甲比乙的成绩稳定.
故选:A.
9、甲、乙、丙、丁四位同学在五次数学测验中,他们成绩的平均分相等,方差分别是2.3、3.8、5.2、6.2,则成绩最稳定的同学是( )
A.甲 B.乙 C.丙 D.丁
【答案】A
【分析】
方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好,据此判断出成绩最稳定的同学是谁即可.
【详解】
解:∵2.3<3.8<5.2<6.2,
∴S甲2<S乙2<S丙2<S丁2,
∴成绩最稳定的是甲.
故选:A.
10、八年级一,二班的同学在一次数学测验中的成绩统计情况如下表:
班级 参加人数 中位数 平均数 方差
一
二
某同学分析后得到如下结论:①一,二班学生成绩平均水平相同;②二班优生人数不少于一班(优生线分);③一班学生的成绩相对稳定.其中正确的是( )
A.②③ B.①② C.①③ D.①②③
【答案】B
【分析】
根据平均水平的判断主要分析平均数;优秀人数的判断从中位数不同可以得到;波动大小比较方差的大小.
【详解】
解:从表中可知,平均成绩都是80,故①正确;
一班的中位数是84,二班的中位数是85,由于优生线85分,故二班优生人数多于一班,故②正确;
一班的方差大于二班的,又说明一班的波动情况大,所以③错误.
故选:B
二、填空题
11、如果一组数据,,,,的平均数是,那么是_____.
【答案】5
【分析】
运用平均数的计算公式即可求得x的值.
【详解】
根据题意知:(2+6+3+4+x)÷5=4,
解得:x=5,
故答案是:5.
12、某校学生的数学期末总评成绩由平时成绩、期中成绩、期末成绩3个部分组成,各部分比例如图所示.小明这三项的成绩依次是90分,85分,92分,则小明的期末总评成绩是_____.
【答案】89.3分
【分析】根据加权平均数的定义计算可得.
【详解】解:小明的期末总评成绩是90×30%+85×30%+92×40%=89.3(分),
故答案为:89.3分.
13、某市在一次空气污染指数抽查中,收集到7天的数据如下:60,75,70,60,56,75,60.该组数据的中位数是__,众数是__.
【答案】60 60
【分析】
把数据按顺序排列后,再根据中位数和众数的定义可以得到解答.
【详解】
解:将这组数据按从小到大的顺序排列为56,60,60,60,70,75,75,处于中间位置的那个数是60,且60出现3次,75出现2次,56、70各出现1次
那么由中位数和众数的定义可知,这组数据的中位数是60,众数是60
故答案为:60,60.
14、在重庆八中“青春飞扬”艺术节的钢琴演奏比赛决赛中,参加比赛的10名选手成绩统计如图所示,则这10名学生成绩的中位数是___________.
【答案】8.5
【解析】
根据图形,这10个学生的分数为:7,7.5,8,8,8.5,8.5,9,9,9,9.5,则中位数为8.5.
故答案:8.5.
15、在预防新型冠状病毒期间,有关部门加强了对市场的监管力度.在对某药店检查中,抽检了6包口罩(每包10只),得到合格的口罩只数分别是7,10,9,10,7,8,则该组数据7,10,9,10,7,8的中位数是_____.
【答案】
【分析】
根据中位数的定义依次计算即可解答.
【详解】
解:按照从小到大的顺序排列为:7、7、8、9、10、10,第3个和第4个数分别是8,9,
故中位数是(8+9)÷2=8.5.
故答案为:8.5.
16、已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是1,则数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的方差是______.
【答案】9
【分析】
先求出数据的平均数,再根据平均数公式与方差公式即可求解.
【详解】
解:∵数据x1,x2,x3,x4,x5的平均数是2,
∴x1+x2+x3+x4+x5=2×5=10,
∴,
∵数据x1,x2,x3,x4,x5的方差是1,
∴[(x1-2)2+(x2-2)2+(x3-2)2+(x4-2)2+(x5-2)2]=1,
∴[(3x1-2-4)2+(3x2-2-4)2+(3x3-2-4)2+(3x4-2-4)2+(3x5-2-4)2]
=[9(x1-2)2+9(x2-2)2+9(x3-2)2+9(x4-2)2+9(x5-2)2]=9×1=9,
故答案为:9.
17、青少年科技创新大赛是一项具有30年历史的全国性青少年科技创新成果和科学探究项目的综合性科技竞赛.某校准备从甲、乙、丙、丁四个科创小组中选出一组参加青少年科技创新大赛.表格反映的是各组平时成绩的平均数(单位:分),及方差,如果要选出一个成绩较好且状态稳定的组去参赛,那么应去的组是________.
甲 乙 丙 丁
7 8 8 7
1 1.2 0.9 1.8
【答案】丙
【分析】
根据方差和平均数的意义进行解答即可.
【详解】
解:∵乙组、丙组的平均数比甲组、丁组大,
∴乙组、丙组优先
∵丙组的方差比乙组的小,
∴丙组的成绩比较稳定,
∴丙组的成绩较好且状态稳定,应选的组是丙组,
故答案为丙.
18、已知一组数据x1,x2,…,xn的方差是s2,则新的一组数据ax1+1,ax2+1,…,axn+1(a为常数,a≠0)的方差是 .(用含a,s2的代数式表示)
【答案】a2s2
【分析】由于一组数据x1、x2、x3…的方差是s2,而一组新数据ax1+1,ax2+1、ax3+1…axn+1中和原来的数据比较可以得到它们之间的联系,由此可以确定一组新数据ax1+1,ax2+1、ax3+1…axn+1的方差.
【详解】解:∵一组数据x1、x2、x3…xn的方差是s2,
∴一组新数据ax1+1,ax2+1、ax3+1…axn+1的方差是a2?s2.
故答案为a2s2.
三、解答题
19、为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在学校实习基地单位时间内现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如图表所示(单位mm):
平均数 方差 完全符合要求个数
A 20 0.026 2
B 20 SB2
根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为哪个同学的成绩好些?
(2)计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些?
(3)考虑图中折线走势,你认为派谁去参赛较合适?说明你的理由.
【答案】(1)B的成绩好些;(2)0.008,B的成绩更好一些;(3)派A去参赛较合适,见解析
【分析】
(1)根据A、B的平均数相同,而B完全符合要求的件数多可得答案;
(2)根据方差的定义计算出SB2的大小,再在平均数相同的情况下比较方差的大小可得答案;
(3)根据潜力的大小判断.
【详解】
解:(1)表中B完全符合的个数为5,根据表中数据可看出,A、B的平均数相同,而B完全符合要求的件数多,B的成绩好些.
(2)∵=×[3×(19.9﹣20)2+5×(20﹣20)2+(20.1﹣20)2+(20.2﹣20)2]=0.008,
,
∴,
∴在平均数相同的情况下,B的波动小,B的成绩更好一些.
(3)从图中折线走势可知,尽管A的成绩前面起伏大,但后来逐渐稳定,误差小,预测A的潜力大,而B比较稳定,潜力小,所以派A去参赛较合适.
20、甲、乙两人在次打靶测试中命中的环数如下:
第一次 第二次 第三次 第四次 第五次
甲
乙
从数据来看,谁的成绩较稳定?请你通过计算方差说明理由.
【答案】甲的成绩更稳定
【分析】
计算出两人成绩的方差,再进行判断.
【详解】
解:甲的平均数为:=8,
∴甲的方差为:=0.4;
乙的平均数为:=8,
∴乙的方差为:=1.6,
因为甲的方差小于乙的方差,
所以甲的成绩更稳定.
21、一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容∶演讲能力∶演讲效果的比例计算选手的综合成绩(百分制),进入决赛的前两名选手的单项成绩如下表所示:
选手 演讲内容 演讲能力 演讲效果
85 95 95
95 85 95
请计算说明哪位选手成绩更优秀.
【答案】选手
【分析】
利用加权平均数的定义进行计算即可得到选手、的综合成绩,进行比较即可得解.
【详解】
解:根据题意得:
选手的综合成绩为:分,
选手的综合成绩为:分
∵
∴选手的成绩更优秀.
22、从某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分四个等级,将调査结果绘制成如下的不完整的条形统计图和扇形统计图.根据图中信息解决下列问题.
(1)共抽取______________名学生,成绩为2分的学生有_________名
(2)求抽取的所有学生成绩的平均数.
【答案】(1)40,8;(2)2.95
【分析】
(1)从两个统计图可得,“4分”的有12人,占调查人数的30%,可求出调查人数,再算出3分的人数,从而得到2分的人数;
(2)根据加权平均数的意义,计算平均数即可.
【详解】
解:(1)依题意得,共抽取学生12÷30%=40(人),
∴成绩为3分的学生有40×42.5%=17(人),
∴成绩为2分的学生有40-17-3-12=8(人),
故答案为:40,8;
(2)抽取的所有学生成绩的平均数是:(1×3+2×8+3×17+4×12)÷40=2.95(分).
答:抽取的所有学生成绩的平均数为2.95分.
23、为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 3首 4首 5首 6首 7首 8首
人数 1 3 5 6 10 15
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为_____________,平均数为___________;
(2)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
【答案】(1)6,5.7;(2)活动初40名学生平均诵背数量为5.7,活动一个月后40名学生平均诵背数量为6.65首;活动初学生一周诗词诵背数量中位数为6首,活动一个月后学生一周诗词诵背数量为7首,该校经典诗词诵背活动效果好
【分析】
(1)根据中位数、平均数的定义求解即可;
(2)从中位数、众数,平均数等多角度分析,只要理由合理即可.
【详解】
解(1)∵把这些数从小到大排列,最中间的数是第20和第21个数的平均数,
∴中位数是:(首);
平均数为:(首);
(2)活动初40名学生平均诵背数量为5.7,活动一个月后40名学生平均诵背数量为6.65首;活动初学生一周诗词诵背数量中位数为6首,活动一个月后学生一周诗词诵背数量中位数为7首;根据以上数据分析,该校经典诗词诵背活动效果好.
24、为提高农民收入,村民自愿投资办起了养鸡场.办场时买来1000只小鸡,经过一段时间,饲养可以出售了.下表是这些鸡出售时质量的统计数据:
质量/ kg 1.0 1.2 1.5 1.8 2
频数 112 230 320 240 98
(1)出售时这些鸡的平均质量是多少(结果保留小数点后一位) ?
(2)质量在哪个值的鸡最多?
(3)中间的质量是多少?
【答案】(1)1.5 kg;(2)质量在1.5kg的鸡最多;(3)1.5 kg
【分析】
(1)根据加权平均数的公式列出算式进行计算,即可完成求解;
(2)结合题意,根据众数的定义,即可得出答案;
(3)结合题意,根据中位数的定义分析,即可得到答案.
【详解】
(1)这些鸡的平均质量为:
=1.496≈1.5 (kg)
(2)根据题意得:质量在1.5kg的鸡最多;
(3)根据题意,1000只鸡中,中间两只鸡的质量均为:1.5kg
∴中间的质量是:1.5 kg.
25、某市举行知识大赛,A校.B校各派出5名选手组成代表队参加比赛.两校派出选手的比赛成绩如图所示.
根据以上信息.整理分析数据如表:
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
(1)a= ;b= ;
(2)填空:(填“A校”或“B校”)
①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是 ;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是 ;
③从两校比赛成绩的方差的角度来比较, 代表队选手成绩的方差较大.
【答案】(1)80,100;(2)①A校;②B校;③B校
【分析】
(1)根据中位数的定义和众数的定义即可求出a和b的值;
(2)①根据平均数和中位数的意义即可得出结论;
②根据平均数和众数的意义即可得出结论;
③求出两个代表队的方差即可得出结论.
【详解】
解:(1)由条形统计图可知:B校5名选手的成绩从小到大排列后分别为:70、75、80、100、100
∴B校5名选手的成绩的中位数为80,众数为100
∴a=80,b=100
故答案为:80,100;
(2)①∵两校的平均数相同,A校的中位数>B校的中位数
∴从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是A校
故答案为:A校;
②∵两校的平均数相同,A校的众数<B校的众数
∴从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是B校
故答案为:B校;
③A校的方差=70
B校的方差=160
∴<
∴从两校比赛成绩的方差的角度来比较,B校代表队选手成绩的方差较大.
故答案为:B校.
一、选择题
1、小颖八年级第一学期的数学成绩分别为:平时90分,期中86分,期末95分若按下图所显示的权重要求计算,则小颖该学期总评成绩为( )
A.88 B. C. D.93
2、8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为( )
A.76 B.75 C.74 D.73
3、我县今年4月某地6天的最高气温如下(单位℃):32,29,30,32,30,32.则这个地区最高气温的众数和中位数分别是( )
A.30,32 B.32,30 C.32,31 D.32,32
4、某商场对上周末某品牌运动服的销售情况进行了统计,如下表所示:经理决定本周进货时多进一些红色的,可用来解释这一现象的统计知识是( )
颜色 黄色 绿色 白色 紫色 红色
数量(件) 120 150 230 75 430
A.平均数 B.中位数
C.众数 D.平均数与中位数
5、在“全民读书月”活动中,小明调查了班级里40名同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图,则这40名同学购买课外书花费的众数和中位数分别为( )
A.30元,30元 B.30元,50元 C.50元,50元 D.50元,80元
6、若样本,,,,的平均数为10,方差为4,则对于样本,,,,,下列结论正确的是( )
A.平均数为10,方差为2 B.众数不变,方差为4
C.平均数为7,方差为2 D.中位数变小,方差不变
7、某班有46人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体划试.因此计算其他45人的平均分为88分,方差为38.后来小亮进行了补测,成绩为88分,关于该班46人的测试成绩,下列说法正确的是( )
A.平均分和方差都不变 B.平均分不变,方差变大
C.平均分不变,方差变小 D.平均分和方差都改变
8、在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是8环,其中甲的成绩的方差,乙的成绩的方差,则( )
A.甲比乙的成绩稳定 B.乙比甲的成绩稳定
C.甲、乙两人的成绩一样稳定 D.无法确定谁的成绩更稳定
9、甲、乙、丙、丁四位同学在五次数学测验中,他们成绩的平均分相等,方差分别是2.3、3.8、5.2、6.2,则成绩最稳定的同学是( )
A.甲 B.乙 C.丙 D.丁
10、八年级一,二班的同学在一次数学测验中的成绩统计情况如下表:
班级 参加人数 中位数 平均数 方差
一
二
某同学分析后得到如下结论:①一,二班学生成绩平均水平相同;②二班优生人数不少于一班(优生线分);③一班学生的成绩相对稳定.其中正确的是( )
A.②③ B.①② C.①③ D.①②③
二、填空题
11、如果一组数据,,,,的平均数是,那么是_____.
12、某校学生的数学期末总评成绩由平时成绩、期中成绩、期末成绩3个部分组成,各部分比例如图所示.小明这三项的成绩依次是90分,85分,92分,则小明的期末总评成绩是_____.
13、某市在一次空气污染指数抽查中,收集到7天的数据如下:60,75,70,60,56,75,60.该组数据的中位数是__,众数是__.
14、在重庆八中“青春飞扬”艺术节的钢琴演奏比赛决赛中,参加比赛的10名选手成绩统计如图所示,则这10名学生成绩的中位数是___________.
15、在预防新型冠状病毒期间,有关部门加强了对市场的监管力度.在对某药店检查中,抽检了6包口罩(每包10只),得到合格的口罩只数分别是7,10,9,10,7,8,则该组数据7,10,9,10,7,8的中位数是_____.
16、已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是1,则数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的方差是______.
17、青少年科技创新大赛是一项具有30年历史的全国性青少年科技创新成果和科学探究项目的综合性科技竞赛.某校准备从甲、乙、丙、丁四个科创小组中选出一组参加青少年科技创新大赛.表格反映的是各组平时成绩的平均数(单位:分),及方差,如果要选出一个成绩较好且状态稳定的组去参赛,那么应去的组是________.
甲 乙 丙 丁
7 8 8 7
1 1.2 0.9 1.8
18、已知一组数据x1,x2,…,xn的方差是s2,则新的一组数据ax1+1,ax2+1,…,axn+1(a为常数,a≠0)的方差是 .(用含a,s2的代数式表示)
三、解答题
19、为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在学校实习基地单位时间内现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如图表所示(单位mm):
平均数 方差 完全符合要求个数
A 20 0.026 2
B 20 SB2
根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为哪个同学的成绩好些?
(2)计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些?
(3)考虑图中折线走势,你认为派谁去参赛较合适?说明你的理由.
20、甲、乙两人在次打靶测试中命中的环数如下:
第一次 第二次 第三次 第四次 第五次
甲
乙
从数据来看,谁的成绩较稳定?请你通过计算方差说明理由.
21、一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容∶演讲能力∶演讲效果的比例计算选手的综合成绩(百分制),进入决赛的前两名选手的单项成绩如下表所示:
选手 演讲内容 演讲能力 演讲效果
85 95 95
95 85 95
22、从某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分四个等级,将调査结果绘制成如下的不完整的条形统计图和扇形统计图.根据图中信息解决下列问题.
(1)共抽取______________名学生,成绩为2分的学生有_________名
(2)求抽取的所有学生成绩的平均数.
23、为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 3首 4首 5首 6首 7首 8首
人数 1 3 5 6 10 15
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为_____________,平均数为___________;
(2)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
24、为提高农民收入,村民自愿投资办起了养鸡场.办场时买来1000只小鸡,经过一段时间,饲养可以出售了.下表是这些鸡出售时质量的统计数据:
质量/ kg 1.0 1.2 1.5 1.8 2
频数 112 230 320 240 98
(1)出售时这些鸡的平均质量是多少(结果保留小数点后一位) ?
(2)质量在哪个值的鸡最多?
(3)中间的质量是多少?
25、某市举行知识大赛,A校.B校各派出5名选手组成代表队参加比赛.两校派出选手的比赛成绩如图所示.
根据以上信息.整理分析数据如表:
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
(1)a= ;b= ;
(2)填空:(填“A校”或“B校”)
①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是 ;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是 ;
③从两校比赛成绩的方差的角度来比较, 代表队选手成绩的方差较大.
专题复习提升训练卷20.4《数据的分析》单元训练(2)-20-21人教版八年级数学下册(解析)
一、选择题
1、小颖八年级第一学期的数学成绩分别为:平时90分,期中86分,期末95分若按下图所显示的权重要求计算,则小颖该学期总评成绩为( )
A.88 B. C. D.93
【答案】B
【分析】根据加权平均数的计算公式即可得.
【详解】由题意得:小颖该学期总评成绩为(分)
故选:B.
2、8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为( )
A.76 B.75 C.74 D.73
【答案】D
【分析】
根据平均数公式即可得到结果.
【详解】
由题意得,
解得
3、我县今年4月某地6天的最高气温如下(单位℃):32,29,30,32,30,32.则这个地区最高气温的众数和中位数分别是( )
A.30,32 B.32,30 C.32,31 D.32,32
【答案】C
【分析】
根据众数和中位数的定义,结合所给数据即可得出答案.
【详解】
解:将这组数据按从小到大的顺序排列为:29,30,30,32,32,32,
出现最多的数字为:32,故众数是32,
中位数为第3、4个数的平均数,即为.
故选:C.
4、某商场对上周末某品牌运动服的销售情况进行了统计,如下表所示:经理决定本周进货时多进一些红色的,可用来解释这一现象的统计知识是( )
颜色 黄色 绿色 白色 紫色 红色
数量(件) 120 150 230 75 430
A.平均数 B.中位数
C.众数 D.平均数与中位数
【答案】C
【分析】
商场经理最值得关注的应该是爱买哪种颜色运动服的人数最多,即众数.
【详解】
解:由于销售最多的颜色为红色,且远远多于其他颜色,所以选择多进红色运动服的主要根据众数.
故选:C
5、在“全民读书月”活动中,小明调查了班级里40名同学本学期购买课外书的花费情况,并将结果绘制成如图所示的统计图,则这40名同学购买课外书花费的众数和中位数分别为( )
A.30元,30元 B.30元,50元 C.50元,50元 D.50元,80元
【答案】B
【分析】
众数就是出现次数最多的数,据此即可判断;中位数就是数据从小到大排列后,处于中间位置的数或中间两数的平均数,根据定义判断即可.
【详解】
解:∵购买课外书花费30元的有12人,人数最多,
∴众数是30元;
把这些数从小到大排列,最中间的两个数是第20和第21个数,都是50元,
则中位数是(元);
故选:B.
6、若样本,,,,的平均数为10,方差为4,则对于样本,,,,,下列结论正确的是( )
A.平均数为10,方差为2 B.众数不变,方差为4
C.平均数为7,方差为2 D.中位数变小,方差不变
【答案】D
【分析】
利用平均数、中位数、众数和方差的意义进行判断.
【详解】
解:∵样本x1,x2,x3,…,xn的平均数为10,方差为4,
∴样本x1﹣3,x2﹣3,x3﹣3,…,xn﹣3
的平均数为 =7,
原众数和中位数减小了3,方差为各数据偏离平均数的平方,各数都减小了3,平均数也减小了3,但偏离平均数的程度不变,故方差不变.
故选:D.
7、某班有46人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体划试.因此计算其他45人的平均分为88分,方差为38.后来小亮进行了补测,成绩为88分,关于该班46人的测试成绩,下列说法正确的是( )
A.平均分和方差都不变 B.平均分不变,方差变大
C.平均分不变,方差变小 D.平均分和方差都改变
【答案】C
【分析】
根据平均数,方差的定义计算即可.
【详解】
解:∵小亮的成绩和其他45人的平均数相同,都是88分,
该班46人的平均分为:(分),
该班46人的方差为:,
∴该班46人的测试成绩的平均分不变,方差变小,
故选:C.
8、在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是8环,其中甲的成绩的方差,乙的成绩的方差,则( )
A.甲比乙的成绩稳定 B.乙比甲的成绩稳定
C.甲、乙两人的成绩一样稳定 D.无法确定谁的成绩更稳定
【答案】A
【分析】
根据方差的定义,方差越小数据越稳定.
【详解】
解:∵两人的平均成绩相同,S甲2=0.3<S乙2=2.1,方差小的为甲,
∴甲比乙的成绩稳定.
故选:A.
9、甲、乙、丙、丁四位同学在五次数学测验中,他们成绩的平均分相等,方差分别是2.3、3.8、5.2、6.2,则成绩最稳定的同学是( )
A.甲 B.乙 C.丙 D.丁
【答案】A
【分析】
方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好,据此判断出成绩最稳定的同学是谁即可.
【详解】
解:∵2.3<3.8<5.2<6.2,
∴S甲2<S乙2<S丙2<S丁2,
∴成绩最稳定的是甲.
故选:A.
10、八年级一,二班的同学在一次数学测验中的成绩统计情况如下表:
班级 参加人数 中位数 平均数 方差
一
二
某同学分析后得到如下结论:①一,二班学生成绩平均水平相同;②二班优生人数不少于一班(优生线分);③一班学生的成绩相对稳定.其中正确的是( )
A.②③ B.①② C.①③ D.①②③
【答案】B
【分析】
根据平均水平的判断主要分析平均数;优秀人数的判断从中位数不同可以得到;波动大小比较方差的大小.
【详解】
解:从表中可知,平均成绩都是80,故①正确;
一班的中位数是84,二班的中位数是85,由于优生线85分,故二班优生人数多于一班,故②正确;
一班的方差大于二班的,又说明一班的波动情况大,所以③错误.
故选:B
二、填空题
11、如果一组数据,,,,的平均数是,那么是_____.
【答案】5
【分析】
运用平均数的计算公式即可求得x的值.
【详解】
根据题意知:(2+6+3+4+x)÷5=4,
解得:x=5,
故答案是:5.
12、某校学生的数学期末总评成绩由平时成绩、期中成绩、期末成绩3个部分组成,各部分比例如图所示.小明这三项的成绩依次是90分,85分,92分,则小明的期末总评成绩是_____.
【答案】89.3分
【分析】根据加权平均数的定义计算可得.
【详解】解:小明的期末总评成绩是90×30%+85×30%+92×40%=89.3(分),
故答案为:89.3分.
13、某市在一次空气污染指数抽查中,收集到7天的数据如下:60,75,70,60,56,75,60.该组数据的中位数是__,众数是__.
【答案】60 60
【分析】
把数据按顺序排列后,再根据中位数和众数的定义可以得到解答.
【详解】
解:将这组数据按从小到大的顺序排列为56,60,60,60,70,75,75,处于中间位置的那个数是60,且60出现3次,75出现2次,56、70各出现1次
那么由中位数和众数的定义可知,这组数据的中位数是60,众数是60
故答案为:60,60.
14、在重庆八中“青春飞扬”艺术节的钢琴演奏比赛决赛中,参加比赛的10名选手成绩统计如图所示,则这10名学生成绩的中位数是___________.
【答案】8.5
【解析】
根据图形,这10个学生的分数为:7,7.5,8,8,8.5,8.5,9,9,9,9.5,则中位数为8.5.
故答案:8.5.
15、在预防新型冠状病毒期间,有关部门加强了对市场的监管力度.在对某药店检查中,抽检了6包口罩(每包10只),得到合格的口罩只数分别是7,10,9,10,7,8,则该组数据7,10,9,10,7,8的中位数是_____.
【答案】
【分析】
根据中位数的定义依次计算即可解答.
【详解】
解:按照从小到大的顺序排列为:7、7、8、9、10、10,第3个和第4个数分别是8,9,
故中位数是(8+9)÷2=8.5.
故答案为:8.5.
16、已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是1,则数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的方差是______.
【答案】9
【分析】
先求出数据的平均数,再根据平均数公式与方差公式即可求解.
【详解】
解:∵数据x1,x2,x3,x4,x5的平均数是2,
∴x1+x2+x3+x4+x5=2×5=10,
∴,
∵数据x1,x2,x3,x4,x5的方差是1,
∴[(x1-2)2+(x2-2)2+(x3-2)2+(x4-2)2+(x5-2)2]=1,
∴[(3x1-2-4)2+(3x2-2-4)2+(3x3-2-4)2+(3x4-2-4)2+(3x5-2-4)2]
=[9(x1-2)2+9(x2-2)2+9(x3-2)2+9(x4-2)2+9(x5-2)2]=9×1=9,
故答案为:9.
17、青少年科技创新大赛是一项具有30年历史的全国性青少年科技创新成果和科学探究项目的综合性科技竞赛.某校准备从甲、乙、丙、丁四个科创小组中选出一组参加青少年科技创新大赛.表格反映的是各组平时成绩的平均数(单位:分),及方差,如果要选出一个成绩较好且状态稳定的组去参赛,那么应去的组是________.
甲 乙 丙 丁
7 8 8 7
1 1.2 0.9 1.8
【答案】丙
【分析】
根据方差和平均数的意义进行解答即可.
【详解】
解:∵乙组、丙组的平均数比甲组、丁组大,
∴乙组、丙组优先
∵丙组的方差比乙组的小,
∴丙组的成绩比较稳定,
∴丙组的成绩较好且状态稳定,应选的组是丙组,
故答案为丙.
18、已知一组数据x1,x2,…,xn的方差是s2,则新的一组数据ax1+1,ax2+1,…,axn+1(a为常数,a≠0)的方差是 .(用含a,s2的代数式表示)
【答案】a2s2
【分析】由于一组数据x1、x2、x3…的方差是s2,而一组新数据ax1+1,ax2+1、ax3+1…axn+1中和原来的数据比较可以得到它们之间的联系,由此可以确定一组新数据ax1+1,ax2+1、ax3+1…axn+1的方差.
【详解】解:∵一组数据x1、x2、x3…xn的方差是s2,
∴一组新数据ax1+1,ax2+1、ax3+1…axn+1的方差是a2?s2.
故答案为a2s2.
三、解答题
19、为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在学校实习基地单位时间内现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如图表所示(单位mm):
平均数 方差 完全符合要求个数
A 20 0.026 2
B 20 SB2
根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为哪个同学的成绩好些?
(2)计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些?
(3)考虑图中折线走势,你认为派谁去参赛较合适?说明你的理由.
【答案】(1)B的成绩好些;(2)0.008,B的成绩更好一些;(3)派A去参赛较合适,见解析
【分析】
(1)根据A、B的平均数相同,而B完全符合要求的件数多可得答案;
(2)根据方差的定义计算出SB2的大小,再在平均数相同的情况下比较方差的大小可得答案;
(3)根据潜力的大小判断.
【详解】
解:(1)表中B完全符合的个数为5,根据表中数据可看出,A、B的平均数相同,而B完全符合要求的件数多,B的成绩好些.
(2)∵=×[3×(19.9﹣20)2+5×(20﹣20)2+(20.1﹣20)2+(20.2﹣20)2]=0.008,
,
∴,
∴在平均数相同的情况下,B的波动小,B的成绩更好一些.
(3)从图中折线走势可知,尽管A的成绩前面起伏大,但后来逐渐稳定,误差小,预测A的潜力大,而B比较稳定,潜力小,所以派A去参赛较合适.
20、甲、乙两人在次打靶测试中命中的环数如下:
第一次 第二次 第三次 第四次 第五次
甲
乙
从数据来看,谁的成绩较稳定?请你通过计算方差说明理由.
【答案】甲的成绩更稳定
【分析】
计算出两人成绩的方差,再进行判断.
【详解】
解:甲的平均数为:=8,
∴甲的方差为:=0.4;
乙的平均数为:=8,
∴乙的方差为:=1.6,
因为甲的方差小于乙的方差,
所以甲的成绩更稳定.
21、一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容∶演讲能力∶演讲效果的比例计算选手的综合成绩(百分制),进入决赛的前两名选手的单项成绩如下表所示:
选手 演讲内容 演讲能力 演讲效果
85 95 95
95 85 95
请计算说明哪位选手成绩更优秀.
【答案】选手
【分析】
利用加权平均数的定义进行计算即可得到选手、的综合成绩,进行比较即可得解.
【详解】
解:根据题意得:
选手的综合成绩为:分,
选手的综合成绩为:分
∵
∴选手的成绩更优秀.
22、从某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分四个等级,将调査结果绘制成如下的不完整的条形统计图和扇形统计图.根据图中信息解决下列问题.
(1)共抽取______________名学生,成绩为2分的学生有_________名
(2)求抽取的所有学生成绩的平均数.
【答案】(1)40,8;(2)2.95
【分析】
(1)从两个统计图可得,“4分”的有12人,占调查人数的30%,可求出调查人数,再算出3分的人数,从而得到2分的人数;
(2)根据加权平均数的意义,计算平均数即可.
【详解】
解:(1)依题意得,共抽取学生12÷30%=40(人),
∴成绩为3分的学生有40×42.5%=17(人),
∴成绩为2分的学生有40-17-3-12=8(人),
故答案为:40,8;
(2)抽取的所有学生成绩的平均数是:(1×3+2×8+3×17+4×12)÷40=2.95(分).
答:抽取的所有学生成绩的平均数为2.95分.
23、为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 3首 4首 5首 6首 7首 8首
人数 1 3 5 6 10 15
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为_____________,平均数为___________;
(2)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
【答案】(1)6,5.7;(2)活动初40名学生平均诵背数量为5.7,活动一个月后40名学生平均诵背数量为6.65首;活动初学生一周诗词诵背数量中位数为6首,活动一个月后学生一周诗词诵背数量为7首,该校经典诗词诵背活动效果好
【分析】
(1)根据中位数、平均数的定义求解即可;
(2)从中位数、众数,平均数等多角度分析,只要理由合理即可.
【详解】
解(1)∵把这些数从小到大排列,最中间的数是第20和第21个数的平均数,
∴中位数是:(首);
平均数为:(首);
(2)活动初40名学生平均诵背数量为5.7,活动一个月后40名学生平均诵背数量为6.65首;活动初学生一周诗词诵背数量中位数为6首,活动一个月后学生一周诗词诵背数量中位数为7首;根据以上数据分析,该校经典诗词诵背活动效果好.
24、为提高农民收入,村民自愿投资办起了养鸡场.办场时买来1000只小鸡,经过一段时间,饲养可以出售了.下表是这些鸡出售时质量的统计数据:
质量/ kg 1.0 1.2 1.5 1.8 2
频数 112 230 320 240 98
(1)出售时这些鸡的平均质量是多少(结果保留小数点后一位) ?
(2)质量在哪个值的鸡最多?
(3)中间的质量是多少?
【答案】(1)1.5 kg;(2)质量在1.5kg的鸡最多;(3)1.5 kg
【分析】
(1)根据加权平均数的公式列出算式进行计算,即可完成求解;
(2)结合题意,根据众数的定义,即可得出答案;
(3)结合题意,根据中位数的定义分析,即可得到答案.
【详解】
(1)这些鸡的平均质量为:
=1.496≈1.5 (kg)
(2)根据题意得:质量在1.5kg的鸡最多;
(3)根据题意,1000只鸡中,中间两只鸡的质量均为:1.5kg
∴中间的质量是:1.5 kg.
25、某市举行知识大赛,A校.B校各派出5名选手组成代表队参加比赛.两校派出选手的比赛成绩如图所示.
根据以上信息.整理分析数据如表:
平均数/分 中位数/分 众数/分
A校 85 85 85
B校 85 a b
(1)a= ;b= ;
(2)填空:(填“A校”或“B校”)
①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是 ;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是 ;
③从两校比赛成绩的方差的角度来比较, 代表队选手成绩的方差较大.
【答案】(1)80,100;(2)①A校;②B校;③B校
【分析】
(1)根据中位数的定义和众数的定义即可求出a和b的值;
(2)①根据平均数和中位数的意义即可得出结论;
②根据平均数和众数的意义即可得出结论;
③求出两个代表队的方差即可得出结论.
【详解】
解:(1)由条形统计图可知:B校5名选手的成绩从小到大排列后分别为:70、75、80、100、100
∴B校5名选手的成绩的中位数为80,众数为100
∴a=80,b=100
故答案为:80,100;
(2)①∵两校的平均数相同,A校的中位数>B校的中位数
∴从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是A校
故答案为:A校;
②∵两校的平均数相同,A校的众数<B校的众数
∴从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是B校
故答案为:B校;
③A校的方差=70
B校的方差=160
∴<
∴从两校比赛成绩的方差的角度来比较,B校代表队选手成绩的方差较大.
故答案为:B校.
