江苏省无锡市江阴市高中2020-2021学年高一下学期5月月考数学试题 Word版含答案
文档属性
| 名称 | 江苏省无锡市江阴市高中2020-2021学年高一下学期5月月考数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 987.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 21:59:29 | ||
图片预览




文档简介
江阴市高中2020-2021学年度第二学期5月份阶段性测试试卷
高一数学
一、选择题(共60分,1-8为单选题,9-12为多选题)
1.已知复数false(false为虚数单位),则( )
A.false的实部为3 B.false的虚部为false
C.false D.false的共轭复数为false
2.某地8名新冠肺炎病患者的潜伏期(单位:天)分别为7,8,8,12,11,10,14,16,则它们的75%分位数是( )
A.12 B.13 C.14 D.15
3.如图正方形false的边长为1,它是水平放置的一个平面图形的直观图,则原图形的面积( )
A.false B.1 C.false D.false
4.抛掷2枚质地均匀的骰子,向上的点数之差的绝对值为3的概率是( )
A.false B.false C.false D.false
5.已知在false中,false,false,false,则false( )
A.false B.false C.false D.false
6.设false是直线,false,false是两个不同的平面( )
A.若false,false,则false B.若false,false,则false
C.若false,false,则false D.若false,false,则false
7.我国古代数学名著《九章算术》中记载:“刍甍(chu meng)者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”今有底面为正方形的屋脊形状的多面体(如图所示),下底面是边长为2的正方形,上棱false,false平面false,false与平面false的距离为2,该刍甍的体积为( )
A.6 B.false C.false D.12
8.在false中,false,false,以false为边作等腰直角三角形false(false为直角顶点,false,false两点在直线false的两侧).当角false变化时,线段false长度的最大值是( )
A.3 B.4 C.5 D.9
9.下列关于向量false,false,false的运算,一定成立的有( )
A.false B.false
C.false D.false
10.已知甲、乙两名同学在高三的6次数学测试的成绩统计如图,则下列说法正确的是( )
A.若甲、乙两组数据的平均数分别为false,false,则false
B.若甲、乙两组数据的方差分别为false,false,则false
C.甲成绩的极差小于乙成绩的极差
D.甲成绩比乙成绩稳定
11.已知甲罐中有四个相同的小球,标号分别为1,2,3,4,乙罐中有五个相同的小球,标号分别为1,2,3,5,6.现从甲罐、乙罐中分别随机抽取1个小球,记事件false“抽取的两个小球标号之和大于5”,事件false“抽取的两个小球标号之积大于8”,则( )
A.事件false发生的概率为false B.事件false发生的概率为false
C.事件false发生的概率为false D.至少抽到一个有标号为3的小球的概率为false
12.我们把所有棱长都相等的正棱柱(锥)叫“等长正棱柱(锥)”,而与其所有棱都相切的球称为棱切球,设下列“等长正棱柱(锥)”的棱长都为1,则下列说法中正确的有( )
A.正方体的棱切球的半径为false
B.正四面体的棱切球的表面积为false
C.等长正六棱柱的棱切球的体积为false
D.等长正四棱锥的棱切球被棱锥5个面(侧面和底面)截得的截面面积之和为false
二、填空题(共20分)
13.设false的内角false,false,false所对的边分别为false,false,false,若false,则角false的弧度数是__________.
14.已知样本1,2,4,false,false的平均数是3,标准差是2,则false的值是__________.
15.四棱锥false的底面是一个正方形,false平面false,false,false是棱false的中点,则异面直线false与false所成角的余弦值是_________
16.已知false的外心为false,满足false,则false的最小值是__________.
三、解答题(共70分,17题10分,其它每题12分)
17.已知false是复数,false为实数,false为纯虚数(false为虚数单位).
(1)求复数false;
(2)求false的模;
(3)已知复数false,满足false,求false的最小值.
18.请从下面三个条件中任选一个,补充在下面的横线上,并解答.
①false,②false,false为虚数单位,③false的面积为false.
在false中,内角false,false,false所对的边分别为false,false,false,已知false,false,___________.
(1)求false;
(2)求false的值.
注:如选择多个条件分别解答,按第一个解答计分.
19.如图,在正三棱柱false中,已知false,false分别为false,false的中点,点false在棱false上,且false.
求证:
(1)直线false平面false;
(2)直线false平面false.
20.2020年开始,山东推行全新的高考制度,新高考不再分文理科,采用“false”模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还需要依据想考取的高校及专业要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科满分100分.2020年初受疫情影响,全国各地推迟开学,开展线上教学,为了了解高一学生的选科意向,某学校对学生所选科目进行线上检测,下面是100名学生的物理、化学、生物三科总分成绩,以20为组距分成7组:false,false,false,false,false,false,false,画出频率分布直方图如图所示.
(1)求频率分布直方图中false的值;
(2)
(i)求物理、化学、生物三科总分成绩的中位数;
(ii)估计这100名学生的物理、化学、生物三科总分成绩的平均数(同一组中的数据用该组区间的中点值作代表);
(3)为了进一步了解选科情况,在物理、化学、生物三科总分成绩在false和false的两组中,用比例分配的分层随机抽样方法抽取7名学生,再从这7名学生中随机抽取2名学生进行问卷调查,求抽取的这2名学生来自不同组的概率.
21.在false中,false分别为角false的对边,false其中false为钝角.
(1)证明:false
(2)求false的取值范围.
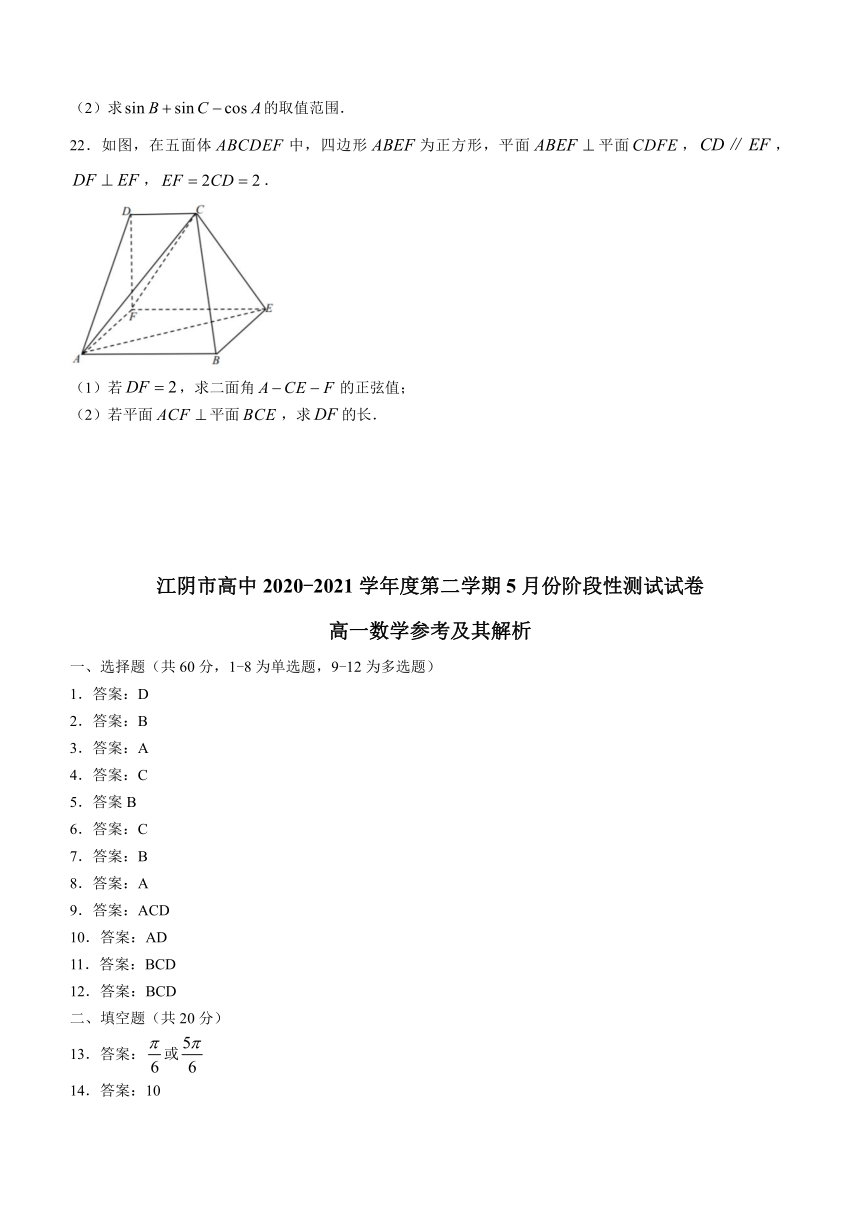
22.如图,在五面体false中,四边形false为正方形,平面false平面false,false,false,false.
(1)若false,求二面角false的正弦值;
(2)若平面false平面false,求false的长.
江阴市高中2020-2021学年度第二学期5月份阶段性测试试卷
高一数学参考及其解析
一、选择题(共60分,1-8为单选题,9-12为多选题)
1.答案:D
2.答案:B
3.答案:A
4.答案:C
5.答案B
6.答案:C
7.答案:B
8.答案:A
9.答案:ACD
10.答案:AD
11.答案:BCD
12.答案:BCD
二、填空题(共20分)
13.答案:false或false
14.答案:10
15.答案:false
16.答案:false
三、解答题(共70分,17题10分,其它每题12分)
17.【解】(1)设false,false,false
∵false为实数,false为纯虚数
∴false,false,∴false
(2)false
∴false
∴false的模为false.
(3)令false
由false,得false.
false
∴false表示圆false上一点false到false的距离.
∴false.
18.【解】
方案一:选择条件①
(1)∵false,false,∴false
由false,解得false或false(舍去),
∴false,∴false
(2)∵false
∴false
false
方案二:选择条件②
(1)由false,解得false或false(舍去),
∴false,∴false
(2)同方案一
方案三:选择条件③
(1)∵false,∴false,
又∵false
∴false
由false,解得false或false(舍去),
∴false,∴false
(2)同方案一
注意:方案二、方案三评分标准参照方案一
19.(1)证明:连结false,因为false,false分别为false,false的中点,所以false且false,所以四边形false是平行四边形,
所以false且false.
又false且false,
所以false且false,
所以四边形false是平行四边形,
所以false.
因为false平面false,false平面false,
所以直线false平面false.
(2)在正三棱柱false中,false平面false,
又false平面false,所以false.
又false是正三角形,且false为false的中点,
所以false.
又false,false平面false,false,
所以false平面false.
又false平面false,所以false.
又false,false,false平面false,false.
所以直线false平面false.
20.【解】(1)由题图得,
false,
解得false
(2)(i)因为
false,
false,
所以三科总分成绩的中位数在false内,设中位数为false,
则false,解得false,即中位数为224.
(ii)三科总分成绩的平均数为
false
(3)三科总分成绩在false,false两组内的学生分别有25人,10人,
故抽样比为false.
所以从三科总分成绩在false,false两组中抽取的学生人数
分别false,false.
记事件false“抽取的这2名学生来自不同组”.
三科总分成绩在false内的5人分别记为false,false,false,false,false,在false内的2人分别记为false,false.
现在这7人中抽取2人,则试验的样本空间false{false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false},共21个样本点.
其中false{false,false,false,false,false,false,false,false,false,false},共10个样本点.
所以false,抽取的这2名学生来自不同组的概率为false.
21.(1)证明:在false中,由正弦定理false得
false,等价于false
因为false,所以false.
所以false.
因为false为钝角,所以false,false,
所以false,即false;
(2)由(1)可得false
false
设false,则false
∵false,∴false
∴false
∴原式false
false
∴取值范围为false∵∴∵∴∵∴∵
22.【解】(1)因为平面false平面false,
平面false平面false,false,false平面false,
所以false平面false,所以false.
又因为false,false平面false,false平面false,false.
所以false平面false.
在平面false内过点false作false于false,连结false,则false.
所以false为二面角false的平面角.
在false中,false,false,
由false,得false.
在false中,false,
所以false,
所以二面角false的正弦值为false.
(2)设平面false平面false.
因为四边形false为正方形,所以false.
又false平面false,false平面false,
所以false平面false.
又false平面false,平面false平面false,所以false.
因为false平面false,false平面false,所以false,所以false.
又平面false平面false,平面false平面false,false平面false,
所以false平面false.
又false平面false,所以false,所以false.
设false,则false,false,
所以false,
解得false,即false.
高一数学
一、选择题(共60分,1-8为单选题,9-12为多选题)
1.已知复数false(false为虚数单位),则( )
A.false的实部为3 B.false的虚部为false
C.false D.false的共轭复数为false
2.某地8名新冠肺炎病患者的潜伏期(单位:天)分别为7,8,8,12,11,10,14,16,则它们的75%分位数是( )
A.12 B.13 C.14 D.15
3.如图正方形false的边长为1,它是水平放置的一个平面图形的直观图,则原图形的面积( )
A.false B.1 C.false D.false
4.抛掷2枚质地均匀的骰子,向上的点数之差的绝对值为3的概率是( )
A.false B.false C.false D.false
5.已知在false中,false,false,false,则false( )
A.false B.false C.false D.false
6.设false是直线,false,false是两个不同的平面( )
A.若false,false,则false B.若false,false,则false
C.若false,false,则false D.若false,false,则false
7.我国古代数学名著《九章算术》中记载:“刍甍(chu meng)者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”今有底面为正方形的屋脊形状的多面体(如图所示),下底面是边长为2的正方形,上棱false,false平面false,false与平面false的距离为2,该刍甍的体积为( )
A.6 B.false C.false D.12
8.在false中,false,false,以false为边作等腰直角三角形false(false为直角顶点,false,false两点在直线false的两侧).当角false变化时,线段false长度的最大值是( )
A.3 B.4 C.5 D.9
9.下列关于向量false,false,false的运算,一定成立的有( )
A.false B.false
C.false D.false
10.已知甲、乙两名同学在高三的6次数学测试的成绩统计如图,则下列说法正确的是( )
A.若甲、乙两组数据的平均数分别为false,false,则false
B.若甲、乙两组数据的方差分别为false,false,则false
C.甲成绩的极差小于乙成绩的极差
D.甲成绩比乙成绩稳定
11.已知甲罐中有四个相同的小球,标号分别为1,2,3,4,乙罐中有五个相同的小球,标号分别为1,2,3,5,6.现从甲罐、乙罐中分别随机抽取1个小球,记事件false“抽取的两个小球标号之和大于5”,事件false“抽取的两个小球标号之积大于8”,则( )
A.事件false发生的概率为false B.事件false发生的概率为false
C.事件false发生的概率为false D.至少抽到一个有标号为3的小球的概率为false
12.我们把所有棱长都相等的正棱柱(锥)叫“等长正棱柱(锥)”,而与其所有棱都相切的球称为棱切球,设下列“等长正棱柱(锥)”的棱长都为1,则下列说法中正确的有( )
A.正方体的棱切球的半径为false
B.正四面体的棱切球的表面积为false
C.等长正六棱柱的棱切球的体积为false
D.等长正四棱锥的棱切球被棱锥5个面(侧面和底面)截得的截面面积之和为false
二、填空题(共20分)
13.设false的内角false,false,false所对的边分别为false,false,false,若false,则角false的弧度数是__________.
14.已知样本1,2,4,false,false的平均数是3,标准差是2,则false的值是__________.
15.四棱锥false的底面是一个正方形,false平面false,false,false是棱false的中点,则异面直线false与false所成角的余弦值是_________
16.已知false的外心为false,满足false,则false的最小值是__________.
三、解答题(共70分,17题10分,其它每题12分)
17.已知false是复数,false为实数,false为纯虚数(false为虚数单位).
(1)求复数false;
(2)求false的模;
(3)已知复数false,满足false,求false的最小值.
18.请从下面三个条件中任选一个,补充在下面的横线上,并解答.
①false,②false,false为虚数单位,③false的面积为false.
在false中,内角false,false,false所对的边分别为false,false,false,已知false,false,___________.
(1)求false;
(2)求false的值.
注:如选择多个条件分别解答,按第一个解答计分.
19.如图,在正三棱柱false中,已知false,false分别为false,false的中点,点false在棱false上,且false.
求证:
(1)直线false平面false;
(2)直线false平面false.
20.2020年开始,山东推行全新的高考制度,新高考不再分文理科,采用“false”模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还需要依据想考取的高校及专业要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科满分100分.2020年初受疫情影响,全国各地推迟开学,开展线上教学,为了了解高一学生的选科意向,某学校对学生所选科目进行线上检测,下面是100名学生的物理、化学、生物三科总分成绩,以20为组距分成7组:false,false,false,false,false,false,false,画出频率分布直方图如图所示.
(1)求频率分布直方图中false的值;
(2)
(i)求物理、化学、生物三科总分成绩的中位数;
(ii)估计这100名学生的物理、化学、生物三科总分成绩的平均数(同一组中的数据用该组区间的中点值作代表);
(3)为了进一步了解选科情况,在物理、化学、生物三科总分成绩在false和false的两组中,用比例分配的分层随机抽样方法抽取7名学生,再从这7名学生中随机抽取2名学生进行问卷调查,求抽取的这2名学生来自不同组的概率.
21.在false中,false分别为角false的对边,false其中false为钝角.
(1)证明:false
(2)求false的取值范围.
22.如图,在五面体false中,四边形false为正方形,平面false平面false,false,false,false.
(1)若false,求二面角false的正弦值;
(2)若平面false平面false,求false的长.
江阴市高中2020-2021学年度第二学期5月份阶段性测试试卷
高一数学参考及其解析
一、选择题(共60分,1-8为单选题,9-12为多选题)
1.答案:D
2.答案:B
3.答案:A
4.答案:C
5.答案B
6.答案:C
7.答案:B
8.答案:A
9.答案:ACD
10.答案:AD
11.答案:BCD
12.答案:BCD
二、填空题(共20分)
13.答案:false或false
14.答案:10
15.答案:false
16.答案:false
三、解答题(共70分,17题10分,其它每题12分)
17.【解】(1)设false,false,false
∵false为实数,false为纯虚数
∴false,false,∴false
(2)false
∴false
∴false的模为false.
(3)令false
由false,得false.
false
∴false表示圆false上一点false到false的距离.
∴false.
18.【解】
方案一:选择条件①
(1)∵false,false,∴false
由false,解得false或false(舍去),
∴false,∴false
(2)∵false
∴false
false
方案二:选择条件②
(1)由false,解得false或false(舍去),
∴false,∴false
(2)同方案一
方案三:选择条件③
(1)∵false,∴false,
又∵false
∴false
由false,解得false或false(舍去),
∴false,∴false
(2)同方案一
注意:方案二、方案三评分标准参照方案一
19.(1)证明:连结false,因为false,false分别为false,false的中点,所以false且false,所以四边形false是平行四边形,
所以false且false.
又false且false,
所以false且false,
所以四边形false是平行四边形,
所以false.
因为false平面false,false平面false,
所以直线false平面false.
(2)在正三棱柱false中,false平面false,
又false平面false,所以false.
又false是正三角形,且false为false的中点,
所以false.
又false,false平面false,false,
所以false平面false.
又false平面false,所以false.
又false,false,false平面false,false.
所以直线false平面false.
20.【解】(1)由题图得,
false,
解得false
(2)(i)因为
false,
false,
所以三科总分成绩的中位数在false内,设中位数为false,
则false,解得false,即中位数为224.
(ii)三科总分成绩的平均数为
false
(3)三科总分成绩在false,false两组内的学生分别有25人,10人,
故抽样比为false.
所以从三科总分成绩在false,false两组中抽取的学生人数
分别false,false.
记事件false“抽取的这2名学生来自不同组”.
三科总分成绩在false内的5人分别记为false,false,false,false,false,在false内的2人分别记为false,false.
现在这7人中抽取2人,则试验的样本空间false{false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false,false},共21个样本点.
其中false{false,false,false,false,false,false,false,false,false,false},共10个样本点.
所以false,抽取的这2名学生来自不同组的概率为false.
21.(1)证明:在false中,由正弦定理false得
false,等价于false
因为false,所以false.
所以false.
因为false为钝角,所以false,false,
所以false,即false;
(2)由(1)可得false
false
设false,则false
∵false,∴false
∴false
∴原式false
false
∴取值范围为false∵∴∵∴∵∴∵
22.【解】(1)因为平面false平面false,
平面false平面false,false,false平面false,
所以false平面false,所以false.
又因为false,false平面false,false平面false,false.
所以false平面false.
在平面false内过点false作false于false,连结false,则false.
所以false为二面角false的平面角.
在false中,false,false,
由false,得false.
在false中,false,
所以false,
所以二面角false的正弦值为false.
(2)设平面false平面false.
因为四边形false为正方形,所以false.
又false平面false,false平面false,
所以false平面false.
又false平面false,平面false平面false,所以false.
因为false平面false,false平面false,所以false,所以false.
又平面false平面false,平面false平面false,false平面false,
所以false平面false.
又false平面false,所以false,所以false.
设false,则false,false,
所以false,
解得false,即false.
同课章节目录
