陕西省西工大附中2012届高三第七次适应性训练 数学理
文档属性
| 名称 | 陕西省西工大附中2012届高三第七次适应性训练 数学理 |  | |
| 格式 | zip | ||
| 文件大小 | 220.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-05 16:17:41 | ||
图片预览


文档简介
2012年普通高等学校招生全国统一考试西工大附中第七次适应性训练
高三数学(理科)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。考试时间120分钟
第Ⅰ卷(选择题 共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合则实数等于( )
A. B.或 C.或 D.
2.函数的零点所在的区间是( )
A.(一2,一1) B.(一1,0) C.(0,1) D.(1,2)
3.下列有关命题的说法中错误的是( )
A.若为假命题,则、均为假命题.
B.“”是“”的充分不必要条件.
C.命题“若则”的逆否命题为:“若则”.
D.对于命题使得<0,则,使.
4.在等差数列中,首项公差,若,则( )
A. B. C. D.
5.二项式展开式中的常数项是( )
A.第7项 B.第8项 C.第9项 D.第10项
6.函数的图象在点处的切线方程是,则( )
A. B. C. D.
7.已知在三棱锥P-ABC中侧面与底面所成的二面角相等,则P点在平面α内的射影一定是△ABC的( )
A.内心 B.外心 C.垂心 D.重心
8. 函数为奇函数,该函数的部分图像如图所示,、分别为最高点与最低点,且,则该函数图象的一条对称轴为 ( )
A. B. C. D.
9.任取,直线与圆相交于M、N两点,则|MN|的概率为 ( )
A. B. C. D.
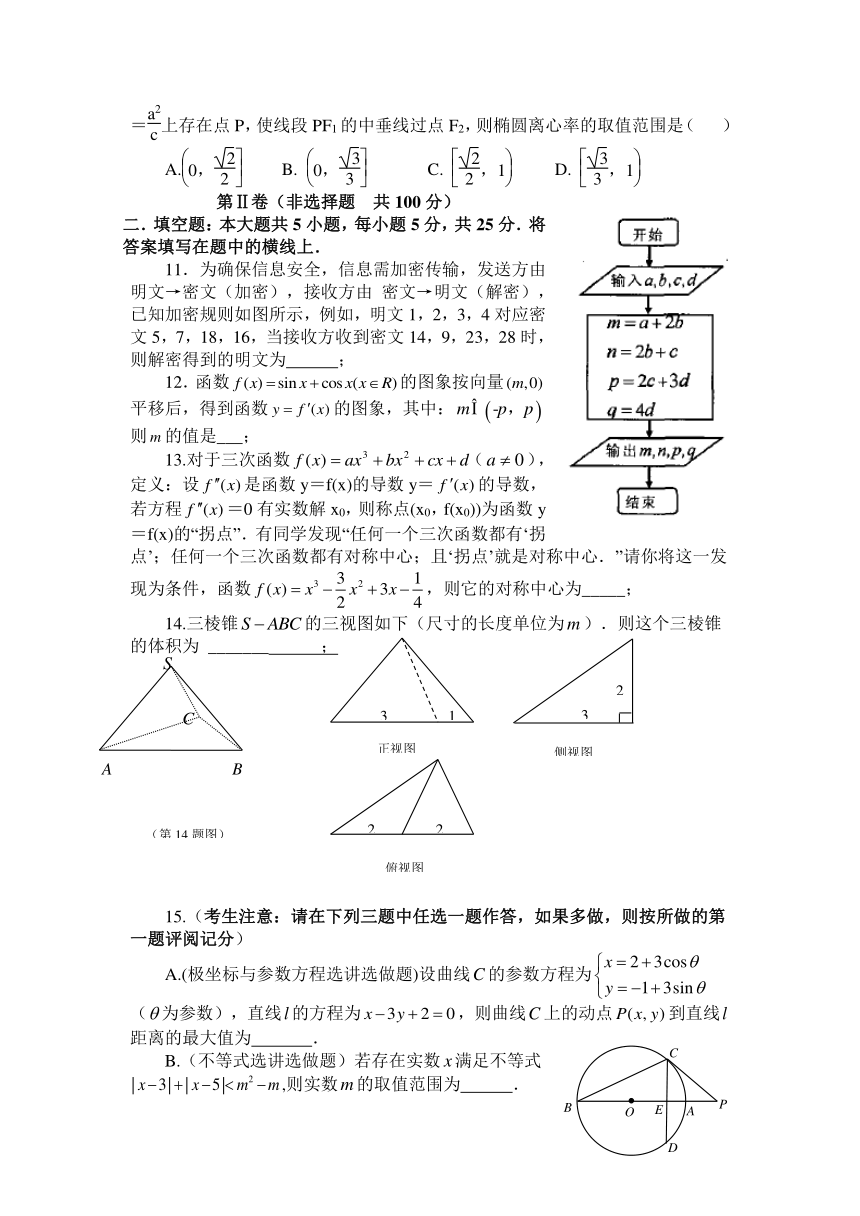
10. 设F1、F2分别为椭圆+=1的左、右焦点,c=,若直线x=上存在点P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
A. B. C. D.
第Ⅱ卷(非选择题 共100分)
二.填空题:本大题共5小题,每小题5分,共25分.将答案填写在题中的横线上.
11.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由 密文→明文(解密),已知加密规则如图所示,例如,明文1,2,3,4对应密文5,7,18,16,当接收方收到密文14,9,23,28时,则解密得到的明文为 ;
12.函数的图象按向量平移后,得到函数的图象,其中:则的值是___;
13.对于三次函数(),定义:设是函数y=f(x)的导数y=的导数,若方程=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,函数,则它的对称中心为_____;
14.三棱锥的三视图如下(尺寸的长度单位为).则这个三棱锥的体积为 _______ ;
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
A.(极坐标与参数方程选讲选做题)设曲线的参数方程为(为参数),直线的方程为,则曲线上的动点到直线距离的最大值为 .
B.(不等式选讲选做题)若存在实数满足不等式,则实数的取值范围为 .
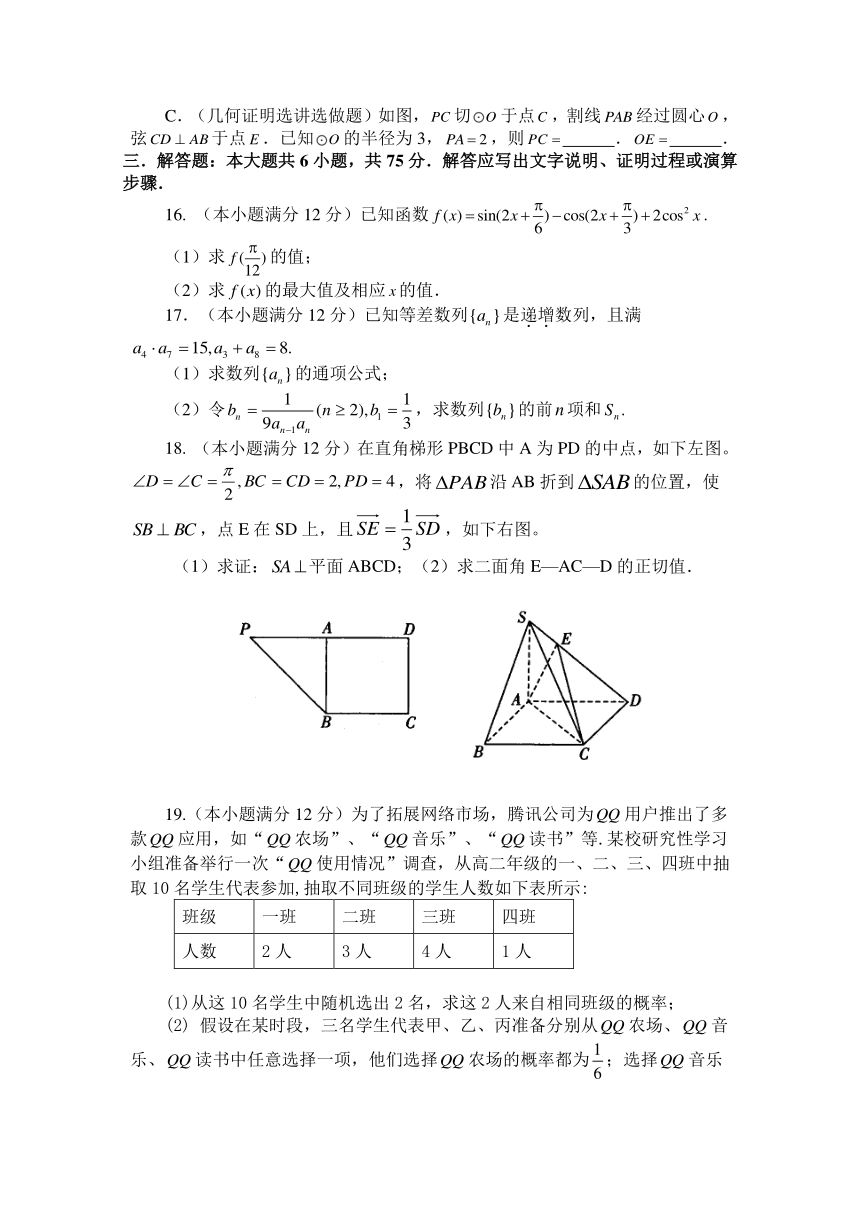
C.(几何证明选讲选做题)如图,切于点,割线经过圆心,弦于点.已知的半径为3,,则 . .
三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16. (本小题满分12分)已知函数.
(1)求的值;
(2)求的最大值及相应的值.
17.(本小题满分12分)已知等差数列是递增数列,且满
(1)求数列的通项公式;
(2)令,求数列的前项和
18. (本小题满分12分)在直角梯形PBCD中A为PD的中点,如下左图。,将沿AB折到的位置,使,点E在SD上,且,如下右图。
(1)求证:平面ABCD;(2)求二面角E—AC—D的正切值.
19.(本小题满分12分)为了拓展网络市场,腾讯公司为用户推出了多款应用,如“农场”、“音乐”、“读书”等.某校研究性学习小组准备举行一次“使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:
班级 一班 二班 三班 四班
人数 2人 3人 4人 1人
(1)从这10名学生中随机选出2名,求这2人来自相同班级的概率;
(2) 假设在某时段,三名学生代表甲、乙、丙准备分别从农场、音乐、读书中任意选择一项,他们选择农场的概率都为;选择音乐的概率都为;选择读书的概率都为;他们的选择相互独立.设在该时段这三名学生中选择读书的总人数为随机变量,求随机变量的分布列及数学期望.
20.(本小题满分13分)已知抛物线,点关于轴的对称点为,直线过点交抛物线于两点.
(1)证明:直线的斜率互为相反数;
(2)求面积的最小值;
(3)当点的坐标为,且.根据(1)(2)推测并回答下列问题(不必说明理由):①直线的斜率是否互为相反数? ②面积的最小值是多少?
21.(本小题满分14分)设函数
(1)若关于x的不等式在有实数解,求实数m的取值范围;
(2)设,若关于x的方程至少有一个解,求p 的最小值.
(3)证明不等式:
2012年普通高等学校招生全国统一考试西工大附中第七次适应性训练
高三数学(理科)参考答案
一、选择题:(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D A C C A D C D
二、填空题:(每小题5分,共25分)
11.6,4,1,7 12. 13. (, 1) 14. 4
15.A. B. C.
三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16. (本小题满分12分)
解:(1)
(2)
,
当时,,
此时,即,
17.(本小题满分12分)
解:(1)根据题意:,知:
是方程的两根,且
解得,
设数列的公差为,由
故等差数列的通项公式为:
(2)当时,
又
18. (本小题满分12分)
解:(1)证明:在图中,由题意可知,
为正方形,所以在图中,,
四边形ABCD是边长为2的正方形,
因为,ABBC,
所以BC平面SAB,………………………3分
又平面SAB,所以BCSA,又SAAB,
所以SA平面ABCD,………………………6分
(2)解法一: 在AD上取一点O,使,连接EO。
因为,所以EO//SA…………………………7分
所以EO平面ABCD,过O作OHAC交AC于H,连接EH,
则AC平面EOH,所以ACEH。
所以为二面角E—AC—D的平面角,………………………9分
在中,…11分
,即二面角E—AC—D的正切值为………12分
解法二:如图,以A为原点建立直角坐标系,
……………7分
易知平面ACD的法向为
设平面EAC的法向量为
……………………9分
由,所以,可取
所以………………………………11分
所以
所以,即二面角E—AC—D的正切值为…………12分
19.(本小题满分12分)
解:(I)记这两名学生都来自第班为事件
则;;;.
∴.…………6分
(Ⅱ)的取值为.
;;
;.
的分布列为:
.或.…………12分
20.(本小题满分13分)
(1)设直线的方程为.
由 可得 .
设,则.-------3分
∴ 又
∴
.
又当垂直于轴时,点关于轴,显然.
综上,. ----------6分
(2)=.
当垂直于轴时,.
∴面积的最小值等于. -----------11分
(3)推测:
①;
②面积的最小值为. ----------- 13分
21.(本小题满分14分)
解:(1)依题意得
,而函数的定义域为
∴在上为减函数,在上为增函数,
则在上为增函数
即实数m的取值范围为
(2)
则
显然,函数在上为减函数,在上为增函数
则函数的最小值为
所以,要使方程至少有一个解,则,即p的最小值为0
(3)由(2)可知: 在上恒成立
所以 ,当且仅当x=0时等号成立
令,则 代入上面不等式得:
即, 即
所以,,,,…,
将以上n个等式相加即可得到:
正视图
侧视图
俯视图
3 1
2 2
3
2
(第14题图)
高三数学(理科)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。考试时间120分钟
第Ⅰ卷(选择题 共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合则实数等于( )
A. B.或 C.或 D.
2.函数的零点所在的区间是( )
A.(一2,一1) B.(一1,0) C.(0,1) D.(1,2)
3.下列有关命题的说法中错误的是( )
A.若为假命题,则、均为假命题.
B.“”是“”的充分不必要条件.
C.命题“若则”的逆否命题为:“若则”.
D.对于命题使得<0,则,使.
4.在等差数列中,首项公差,若,则( )
A. B. C. D.
5.二项式展开式中的常数项是( )
A.第7项 B.第8项 C.第9项 D.第10项
6.函数的图象在点处的切线方程是,则( )
A. B. C. D.
7.已知在三棱锥P-ABC中侧面与底面所成的二面角相等,则P点在平面α内的射影一定是△ABC的( )
A.内心 B.外心 C.垂心 D.重心
8. 函数为奇函数,该函数的部分图像如图所示,、分别为最高点与最低点,且,则该函数图象的一条对称轴为 ( )
A. B. C. D.
9.任取,直线与圆相交于M、N两点,则|MN|的概率为 ( )
A. B. C. D.
10. 设F1、F2分别为椭圆+=1的左、右焦点,c=,若直线x=上存在点P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
A. B. C. D.
第Ⅱ卷(非选择题 共100分)
二.填空题:本大题共5小题,每小题5分,共25分.将答案填写在题中的横线上.
11.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由 密文→明文(解密),已知加密规则如图所示,例如,明文1,2,3,4对应密文5,7,18,16,当接收方收到密文14,9,23,28时,则解密得到的明文为 ;
12.函数的图象按向量平移后,得到函数的图象,其中:则的值是___;
13.对于三次函数(),定义:设是函数y=f(x)的导数y=的导数,若方程=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,函数,则它的对称中心为_____;
14.三棱锥的三视图如下(尺寸的长度单位为).则这个三棱锥的体积为 _______ ;
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
A.(极坐标与参数方程选讲选做题)设曲线的参数方程为(为参数),直线的方程为,则曲线上的动点到直线距离的最大值为 .
B.(不等式选讲选做题)若存在实数满足不等式,则实数的取值范围为 .
C.(几何证明选讲选做题)如图,切于点,割线经过圆心,弦于点.已知的半径为3,,则 . .
三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16. (本小题满分12分)已知函数.
(1)求的值;
(2)求的最大值及相应的值.
17.(本小题满分12分)已知等差数列是递增数列,且满
(1)求数列的通项公式;
(2)令,求数列的前项和
18. (本小题满分12分)在直角梯形PBCD中A为PD的中点,如下左图。,将沿AB折到的位置,使,点E在SD上,且,如下右图。
(1)求证:平面ABCD;(2)求二面角E—AC—D的正切值.
19.(本小题满分12分)为了拓展网络市场,腾讯公司为用户推出了多款应用,如“农场”、“音乐”、“读书”等.某校研究性学习小组准备举行一次“使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:
班级 一班 二班 三班 四班
人数 2人 3人 4人 1人
(1)从这10名学生中随机选出2名,求这2人来自相同班级的概率;
(2) 假设在某时段,三名学生代表甲、乙、丙准备分别从农场、音乐、读书中任意选择一项,他们选择农场的概率都为;选择音乐的概率都为;选择读书的概率都为;他们的选择相互独立.设在该时段这三名学生中选择读书的总人数为随机变量,求随机变量的分布列及数学期望.
20.(本小题满分13分)已知抛物线,点关于轴的对称点为,直线过点交抛物线于两点.
(1)证明:直线的斜率互为相反数;
(2)求面积的最小值;
(3)当点的坐标为,且.根据(1)(2)推测并回答下列问题(不必说明理由):①直线的斜率是否互为相反数? ②面积的最小值是多少?
21.(本小题满分14分)设函数
(1)若关于x的不等式在有实数解,求实数m的取值范围;
(2)设,若关于x的方程至少有一个解,求p 的最小值.
(3)证明不等式:
2012年普通高等学校招生全国统一考试西工大附中第七次适应性训练
高三数学(理科)参考答案
一、选择题:(每小题5分,共50分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D A C C A D C D
二、填空题:(每小题5分,共25分)
11.6,4,1,7 12. 13. (, 1) 14. 4
15.A. B. C.
三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16. (本小题满分12分)
解:(1)
(2)
,
当时,,
此时,即,
17.(本小题满分12分)
解:(1)根据题意:,知:
是方程的两根,且
解得,
设数列的公差为,由
故等差数列的通项公式为:
(2)当时,
又
18. (本小题满分12分)
解:(1)证明:在图中,由题意可知,
为正方形,所以在图中,,
四边形ABCD是边长为2的正方形,
因为,ABBC,
所以BC平面SAB,………………………3分
又平面SAB,所以BCSA,又SAAB,
所以SA平面ABCD,………………………6分
(2)解法一: 在AD上取一点O,使,连接EO。
因为,所以EO//SA…………………………7分
所以EO平面ABCD,过O作OHAC交AC于H,连接EH,
则AC平面EOH,所以ACEH。
所以为二面角E—AC—D的平面角,………………………9分
在中,…11分
,即二面角E—AC—D的正切值为………12分
解法二:如图,以A为原点建立直角坐标系,
……………7分
易知平面ACD的法向为
设平面EAC的法向量为
……………………9分
由,所以,可取
所以………………………………11分
所以
所以,即二面角E—AC—D的正切值为…………12分
19.(本小题满分12分)
解:(I)记这两名学生都来自第班为事件
则;;;.
∴.…………6分
(Ⅱ)的取值为.
;;
;.
的分布列为:
.或.…………12分
20.(本小题满分13分)
(1)设直线的方程为.
由 可得 .
设,则.-------3分
∴ 又
∴
.
又当垂直于轴时,点关于轴,显然.
综上,. ----------6分
(2)=.
当垂直于轴时,.
∴面积的最小值等于. -----------11分
(3)推测:
①;
②面积的最小值为. ----------- 13分
21.(本小题满分14分)
解:(1)依题意得
,而函数的定义域为
∴在上为减函数,在上为增函数,
则在上为增函数
即实数m的取值范围为
(2)
则
显然,函数在上为减函数,在上为增函数
则函数的最小值为
所以,要使方程至少有一个解,则,即p的最小值为0
(3)由(2)可知: 在上恒成立
所以 ,当且仅当x=0时等号成立
令,则 代入上面不等式得:
即, 即
所以,,,,…,
将以上n个等式相加即可得到:
正视图
侧视图
俯视图
3 1
2 2
3
2
(第14题图)
同课章节目录
