陕西省西工大附中2012届高三第五次适应性训练题数学文
文档属性
| 名称 | 陕西省西工大附中2012届高三第五次适应性训练题数学文 |  | |
| 格式 | zip | ||
| 文件大小 | 209.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-05 16:24:32 | ||
图片预览


文档简介
2012年普通高等学校招生全国统一考试西工大附中第五次适应性训练
数 学(文科)
第Ⅰ卷 选择题(共50分)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共10小题,每小题5分,共50分)
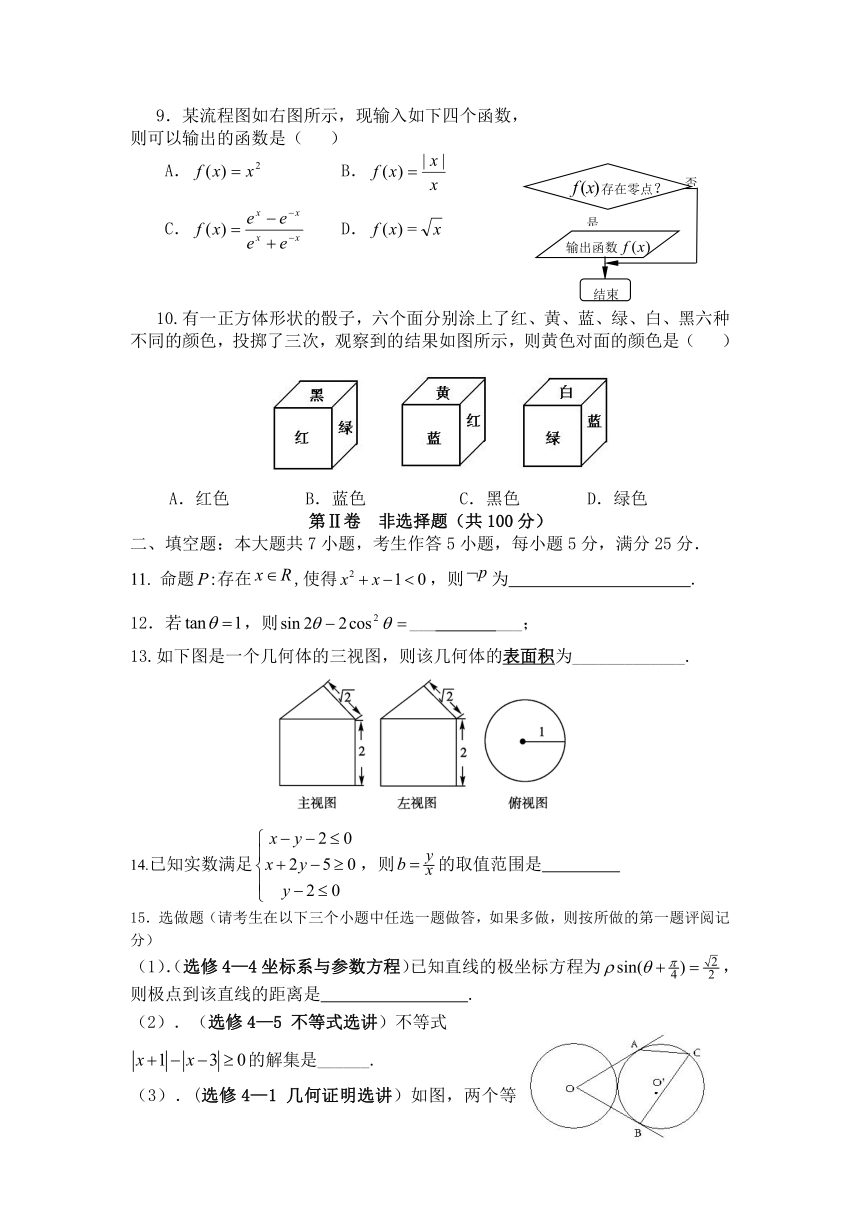
1.已知集合,集合,则( )
A. B. C. D.
2.是的( )
A.充分非必要条件 B. 必要非充分条件
C.充要条件 D.既非充分又非必要条件
3.如图是容量为150的样本的频率分布直方图,则样本数据落在内的频数为( )
A.12 B.48
C.60 D.80
4.双曲线的一条渐近线方程为,则双曲线的离心率为( )
A. B. C. D.
5.已知函数,其导数的
图象如右图,则函数的极小值是 ( )
A. B. C. D.
6.设O为坐标原点,F为抛物线y2=4x的焦点,A是抛物线上一点,若=-4,则点A的坐标是( )
A. B. C.(1,2) D.)
7. 在等差数列中,已知则等于( )
A.40 B. 42 C. 43 D. 45
8.设,函数的导函数是,且是奇函数。若曲线的一条切线的斜率是,则切点的横坐标为( )
A. B. C. D.
9.某流程图如右图所示,现输入如下四个函数,
则可以输出的函数是( )
A. B.
C. D.
10.有一正方体形状的骰子,六个面分别涂上了红、黄、蓝、绿、白、黑六种不同的颜色,投掷了三次,观察到的结果如图所示,则黄色对面的颜色是( )
A.红色 B.蓝色 C.黑色 D.绿色
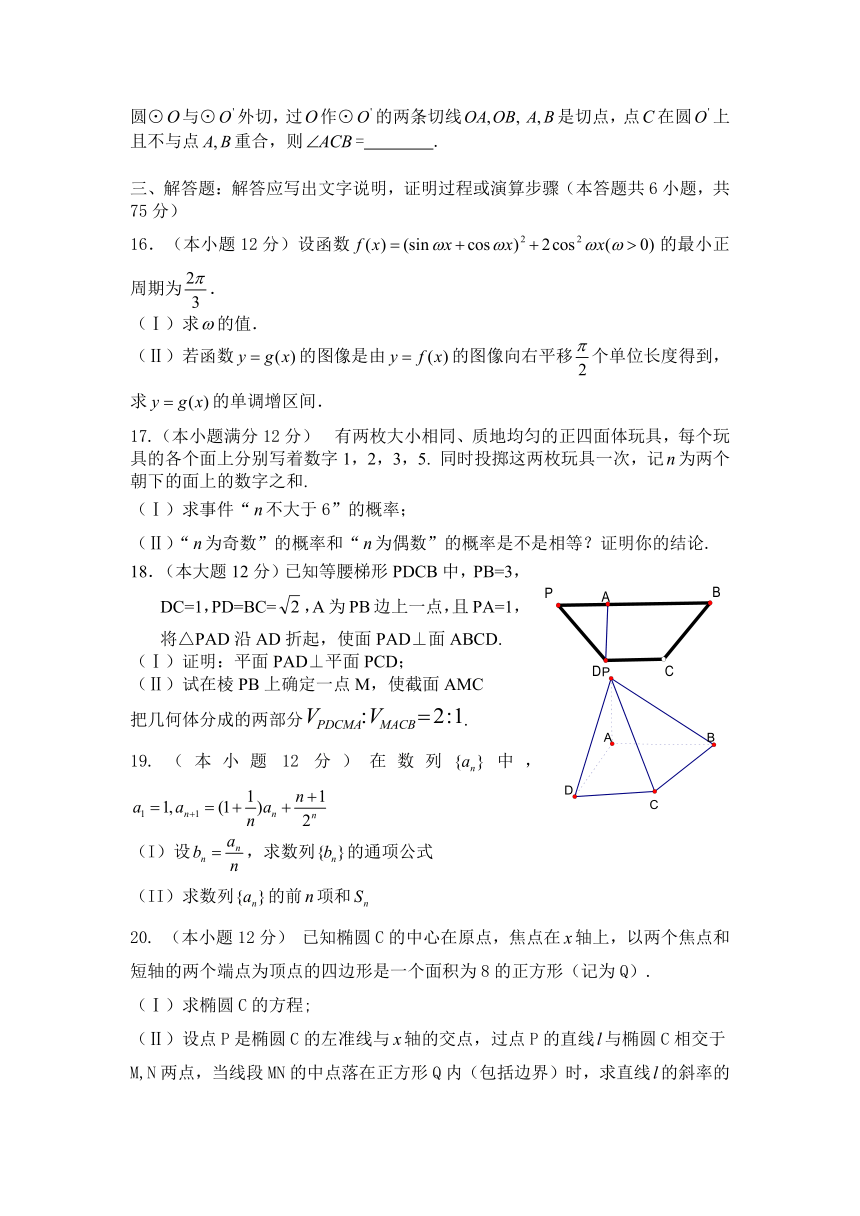
第Ⅱ卷 非选择题(共100分)
二、填空题:本大题共7小题,考生作答5小题,每小题5分,满分25分.
11. 命题存在,使得,则为 .
12.若,则___ ___;
13.如下图是一个几何体的三视图,则该几何体的表面积为_____________.
14.已知实数满足,则的取值范围是
15.选做题(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)
(1).(选修4—4坐标系与参数方程)已知直线的极坐标方程为,则极点到该直线的距离是 .
(2).(选修4—5 不等式选讲)不等式的解集是______.
(3).(选修4—1 几何证明选讲)如图,两个等圆⊙与⊙外切,过作⊙的两条切线是切点,点在圆上且不与点重合,则= .
三、解答题:解答应写出文字说明,证明过程或演算步骤(本答题共6小题,共75分)
16.(本小题12分)设函数的最小正周期为.
(Ⅰ)求的值.
(Ⅱ)若函数的图像是由的图像向右平移个单位长度得到,求的单调增区间.
17.(本小题满分12分)?有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上分别写着数字1,2,3,5. 同时投掷这两枚玩具一次,记为两个朝下的面上的数字之和.
(Ⅰ)求事件“不大于6”的概率;
(Ⅱ)“为奇数”的概率和“为偶数”的概率是不是相等?证明你的结论.
18.(本大题12分)已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.
(Ⅰ)证明:平面PAD⊥平面PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分.
19.(本小题12分)在数列中,
(I)设,求数列的通项公式
(II)求数列的前项和
20. (本小题12分) 已知椭圆C的中心在原点,焦点在轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C的左准线与轴的交点,过点P的直线与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线的斜率的取值范围。
21.(本小题15分)已知函数,其中
若在x=1处取得极值,求a的值;
求的单调区间;
(Ⅲ)若的最小值为1,求a的取值范围。
2012年普通高等学校招生全国统一考试西工大附中第五次适应性训练
数学(文科)参考答案与评分标准
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B A B D B A C D
二、填空题:
11.任意,均有;12. 0;13.; 14. ;
15.(选做题)(1) ; (2) ; (3) .
三、解答题:
16.解:
依题意得,故的值为.
(Ⅱ)依题意得:
由
解得.
故的单调增区间为:
17.(本小题12分) 因玩具是均匀的,所以玩具各面朝下的可能性相等。
所有出现的可能情况共16种:
(1,1),(1,2),(1,3),(1,5),(2,1),(2,2),(2,3),(2,5)
(3,1),(3,2),(3,3),(3,5),(5,1),(5,2),(5,3),(5,5)
(Ⅰ)事件“大于6”包含(2,5),(3,5),(5,2),(5,3),(5,5)
共5个基本事件 ,所以P()=1- =;
(Ⅱ)“为奇数”的概率和“为偶数”的概率不相等。为奇数的概率为 ,
n为偶数的概率为. 所以这两个概率值不相等 .
18.(I)证明:依题意知:
(II)由(I)知平面ABCD
∴平面PAB⊥平面ABCD.在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h, 则
要使
(或M-ABC) 即M为PB的中点.
19.(本小题12分)
(I)由已知有
利用累差迭加即可求出数列的通项公式: ()
(II)由(I)知,=
而,又是一个典型的错位相减法模型,
易得 =
20.(本小题12分)
解: (Ⅰ)依题意,设椭圆C的方程为焦距为,
由题设条件知, 所以
故椭圆C的方程为 .
(Ⅱ)椭圆C的左准线方程为所以点P的坐标,
显然直线的斜率存在,所以直线的方程为。
如图,设点M,N的坐标分别为线段MN的中点为G,
由得. ……①
由解得. ……②
因为是方程①的两根,所以,于是
=, .
因为,所以点G不可能在轴的右边,
又直线,方程分别为
所以点在正方形内(包括边界)的充要条件为 即 亦即解得,此时②也成立. 故直线斜率的取值范围是
21.(本小题14分)
解(Ⅰ)
∵在x=1处取得极值,∴解得
(Ⅱ)
∵ ∴
①当时,在区间∴的单调增区间为
②当时,
由
∴
(Ⅲ)当时,由(Ⅱ)①知,
当时,由(Ⅱ)②知,在处取得最小值
综上可知,若得最小值为1,则a的取值范围是
0
1
2
(第5题图)
开始
输入函数
是
否
存在零点?
否
输出函数
结束
是
8
3
16
2
16
2
16
2
)
7
(
)
5
(
)
3
(
n
P
n
P
n
P
数 学(文科)
第Ⅰ卷 选择题(共50分)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共10小题,每小题5分,共50分)
1.已知集合,集合,则( )
A. B. C. D.
2.是的( )
A.充分非必要条件 B. 必要非充分条件
C.充要条件 D.既非充分又非必要条件
3.如图是容量为150的样本的频率分布直方图,则样本数据落在内的频数为( )
A.12 B.48
C.60 D.80
4.双曲线的一条渐近线方程为,则双曲线的离心率为( )
A. B. C. D.
5.已知函数,其导数的
图象如右图,则函数的极小值是 ( )
A. B. C. D.
6.设O为坐标原点,F为抛物线y2=4x的焦点,A是抛物线上一点,若=-4,则点A的坐标是( )
A. B. C.(1,2) D.)
7. 在等差数列中,已知则等于( )
A.40 B. 42 C. 43 D. 45
8.设,函数的导函数是,且是奇函数。若曲线的一条切线的斜率是,则切点的横坐标为( )
A. B. C. D.
9.某流程图如右图所示,现输入如下四个函数,
则可以输出的函数是( )
A. B.
C. D.
10.有一正方体形状的骰子,六个面分别涂上了红、黄、蓝、绿、白、黑六种不同的颜色,投掷了三次,观察到的结果如图所示,则黄色对面的颜色是( )
A.红色 B.蓝色 C.黑色 D.绿色
第Ⅱ卷 非选择题(共100分)
二、填空题:本大题共7小题,考生作答5小题,每小题5分,满分25分.
11. 命题存在,使得,则为 .
12.若,则___ ___;
13.如下图是一个几何体的三视图,则该几何体的表面积为_____________.
14.已知实数满足,则的取值范围是
15.选做题(请考生在以下三个小题中任选一题做答,如果多做,则按所做的第一题评阅记分)
(1).(选修4—4坐标系与参数方程)已知直线的极坐标方程为,则极点到该直线的距离是 .
(2).(选修4—5 不等式选讲)不等式的解集是______.
(3).(选修4—1 几何证明选讲)如图,两个等圆⊙与⊙外切,过作⊙的两条切线是切点,点在圆上且不与点重合,则= .
三、解答题:解答应写出文字说明,证明过程或演算步骤(本答题共6小题,共75分)
16.(本小题12分)设函数的最小正周期为.
(Ⅰ)求的值.
(Ⅱ)若函数的图像是由的图像向右平移个单位长度得到,求的单调增区间.
17.(本小题满分12分)?有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上分别写着数字1,2,3,5. 同时投掷这两枚玩具一次,记为两个朝下的面上的数字之和.
(Ⅰ)求事件“不大于6”的概率;
(Ⅱ)“为奇数”的概率和“为偶数”的概率是不是相等?证明你的结论.
18.(本大题12分)已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD.
(Ⅰ)证明:平面PAD⊥平面PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分.
19.(本小题12分)在数列中,
(I)设,求数列的通项公式
(II)求数列的前项和
20. (本小题12分) 已知椭圆C的中心在原点,焦点在轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C的左准线与轴的交点,过点P的直线与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线的斜率的取值范围。
21.(本小题15分)已知函数,其中
若在x=1处取得极值,求a的值;
求的单调区间;
(Ⅲ)若的最小值为1,求a的取值范围。
2012年普通高等学校招生全国统一考试西工大附中第五次适应性训练
数学(文科)参考答案与评分标准
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B A B D B A C D
二、填空题:
11.任意,均有;12. 0;13.; 14. ;
15.(选做题)(1) ; (2) ; (3) .
三、解答题:
16.解:
依题意得,故的值为.
(Ⅱ)依题意得:
由
解得.
故的单调增区间为:
17.(本小题12分) 因玩具是均匀的,所以玩具各面朝下的可能性相等。
所有出现的可能情况共16种:
(1,1),(1,2),(1,3),(1,5),(2,1),(2,2),(2,3),(2,5)
(3,1),(3,2),(3,3),(3,5),(5,1),(5,2),(5,3),(5,5)
(Ⅰ)事件“大于6”包含(2,5),(3,5),(5,2),(5,3),(5,5)
共5个基本事件 ,所以P()=1- =;
(Ⅱ)“为奇数”的概率和“为偶数”的概率不相等。为奇数的概率为 ,
n为偶数的概率为. 所以这两个概率值不相等 .
18.(I)证明:依题意知:
(II)由(I)知平面ABCD
∴平面PAB⊥平面ABCD.在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h, 则
要使
(或M-ABC) 即M为PB的中点.
19.(本小题12分)
(I)由已知有
利用累差迭加即可求出数列的通项公式: ()
(II)由(I)知,=
而,又是一个典型的错位相减法模型,
易得 =
20.(本小题12分)
解: (Ⅰ)依题意,设椭圆C的方程为焦距为,
由题设条件知, 所以
故椭圆C的方程为 .
(Ⅱ)椭圆C的左准线方程为所以点P的坐标,
显然直线的斜率存在,所以直线的方程为。
如图,设点M,N的坐标分别为线段MN的中点为G,
由得. ……①
由解得. ……②
因为是方程①的两根,所以,于是
=, .
因为,所以点G不可能在轴的右边,
又直线,方程分别为
所以点在正方形内(包括边界)的充要条件为 即 亦即解得,此时②也成立. 故直线斜率的取值范围是
21.(本小题14分)
解(Ⅰ)
∵在x=1处取得极值,∴解得
(Ⅱ)
∵ ∴
①当时,在区间∴的单调增区间为
②当时,
由
∴
(Ⅲ)当时,由(Ⅱ)①知,
当时,由(Ⅱ)②知,在处取得最小值
综上可知,若得最小值为1,则a的取值范围是
0
1
2
(第5题图)
开始
输入函数
是
否
存在零点?
否
输出函数
结束
是
8
3
16
2
16
2
16
2
)
7
(
)
5
(
)
3
(
n
P
n
P
n
P
同课章节目录
