人教版九年级上册同步练习22.2 二次函数与一元二次方程(word版含答案)
文档属性
| 名称 | 人教版九年级上册同步练习22.2 二次函数与一元二次方程(word版含答案) | 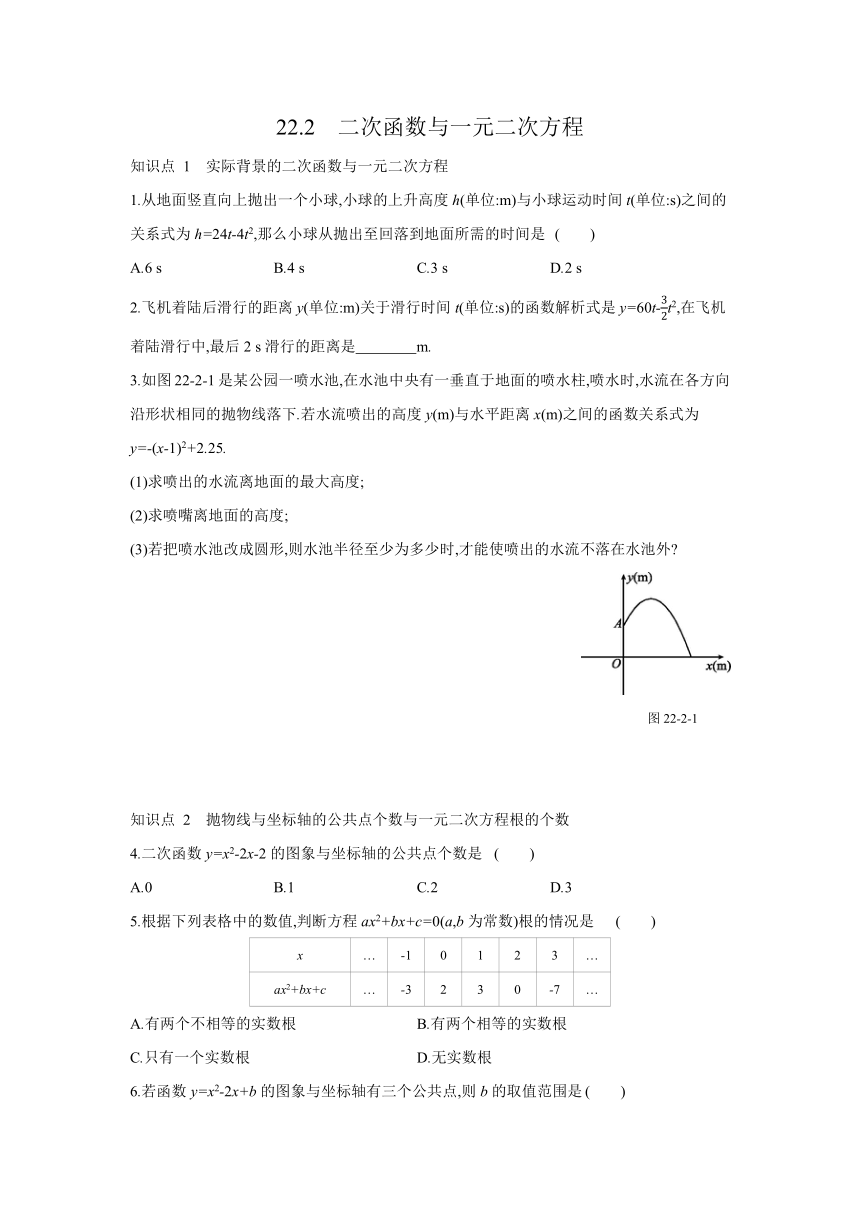 | |
| 格式 | docx | ||
| 文件大小 | 126.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-24 10:25:18 | ||
图片预览



文档简介
22.2 二次函数与一元二次方程
知识点
1 实际背景的二次函数与一元二次方程
1.从地面竖直向上抛出一个小球,小球的上升高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为h=24t-4t2,那么小球从抛出至回落到地面所需的时间是
( )
A.6
s
B.4
s
C.3
s
D.2
s
2.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t-t2,在飞机着陆滑行中,最后2
s滑行的距离是 m.?
3.如图22-2-1是某公园一喷水池,在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25.
(1)求喷出的水流离地面的最大高度;
(2)求喷嘴离地面的高度;
(3)若把喷水池改成圆形,则水池半径至少为多少时,才能使喷出的水流不落在水池外?
图22-2-1
知识点
2 抛物线与坐标轴的公共点个数与一元二次方程根的个数
4.二次函数y=x2-2x-2的图象与坐标轴的公共点个数是
( )
A.0
B.1
C.2
D.3
5.根据下列表格中的数值,判断方程ax2+bx+c=0(a,b为常数)根的情况是
( )
x
…
-1
0
1
2
3
…
ax2+bx+c
…
-3
2
3
0
-7
…
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.无实数根
6.若函数y=x2-2x+b的图象与坐标轴有三个公共点,则b的取值范围是
( )
A.b<1且b≠0
B.b>1
C.0D.b<1
7.已知关于x的函数y=(m-1)x2+2x+m的图象与坐标轴只有2个公共点,则m=
.?
8.已知二次函数y=kx2-6x-9的图象与x轴有两个不同的公共点,则k的取值范围为
.?
9.二次函数y=ax2+bx+c的图象如图22-2-2所示,若方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为
.?
图22-2-2
知识点
3 用图象法估计一元二次方程的根
10.根据下列表格中的对应值,判断方程ax2+bx+c=0(a≠0)的一个根x的取值范围是
( )
x
1.23
1.24
1.25
1.26
ax2+bx+c
-0.07
-0.01
0.04
0.08
A.1.23B.1.24C.1.25D.1命题点
4 利用图象解一元二次不等式
11.若A(-1,0)为抛物线y=-3(x-1)2+c上一点,则当y≥0时,x的取值范围是
( )
A.-1B.x<-1或x>3
C.-1≤x≤3
D.x≤-1或x≥3
12.如图22-2-3,已知抛物线y=x2+2x-3与x轴的两个公共点分别是A,B(点A在点B的左侧).
(1)点A的坐标为 ,点B的坐标为 ;?
(2)利用函数图象,求得当y<5时x的取值范围为 .?
图22-2-3
能力拓展提升
13.已知二次函数y=-x2+x+6及一次函数y=-x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数图象(如图22-2-4所示),当直线y=-x+m与新图象有4个公共点时,m的取值范围是
( )
图22-2-4
A.-B.-C.-2D.-614.如图22-2-5,抛物线y=x2-7x+与x轴交于点A,B,把抛物线在x轴及其下方的部分记作C1,将C1向左平移得到C2,C2与x轴交于点B,D,若直线y=x+m与C1,C2共有3个不同的公共点,则m的取值范围是
( )
图22-2-5
A.-B.-C.-D.-15.已知关于x的二次函数y=ax2-6ax+5a的图象为抛物线C.
(1)求证:当a为任意非零常数时,抛物线C与x轴总有两个不同的公共点;
(2)设抛物线C交x轴于点A,B,交y轴于点D,若△ABD的面积为20,求a的值;
(3)设点E(2,4),F(3,4),若抛物线C与线段EF只有一个公共点,结合函数图象,直接写出a的取值范围.
典题讲评与答案详析
1.A
2.6 [解析]
当y取得最大值时,飞机停下来,
则y=60t-t2=-(t-20)2+600,
此时t=20,飞机着陆后滑行600
m停下来,
因此t的取值范围是0≤t≤20.
当t=18时,y=594,
所以在飞机着陆滑行中,最后2
s滑行的距离是600-594=6(m).
故答案是6.
3.解:(1)∵水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25,
∴喷出的水流离地面的最大高度为2.25
m.
(2)当x=0时,y=-(0-1)2+2.25=1.25,
∴喷嘴离地面的高度为1.25
m.
(3)由题意可得y=0时,0=-(x-1)2+2.25,
解得x1=-0.5(舍去),x2=2.5.
故当水池半径至少为2.5
m时,才能使喷出的水流不落在水池外.
4.D
5.A [解析]
当x=2时,方程ax2+bx+c=0,因此方程有一个实数根为2.当x由-1增大到0时,ax2+bx+c的值由-3增大到2,因此可以推断当x在-1与0之间取某一值时,必有ax2+bx+c=0,说明方程ax2+bx+c=0必有一个根在-1与0之间.
6.A [解析]
∵函数y=x2-2x+b的图象与坐标轴有三个公共点,∴解得b<1且b≠0.
7.1或0或 [解析]
分类讨论:(1)当m-1=0时,m=1,此时函数为一次函数,解析式为y=2x+1,它的图象与x轴的公共点坐标为-,0,与y轴的公共点坐标为(0,1).符合题意.
(2)当m-1≠0时,m≠1,此时函数为二次函数,分两种情况:①图象过原点,且与x轴有两个不同的公共点,于是Δ=4-4(m-1)m>0,解得8.k>-1且k≠0
9.k<2 [解析]
从图象上来看,当k<2时,抛物线y=ax2+bx+c与直线y=k有两个不同的公共点,此时方程ax2+bx+c=k有两个不相等的实数根.
10.B 11.C
12.(1)(-3,0) (1,0) (2)-4[解析]
(1)当x2+2x-3=0时,解得x1=-3,x2=1,∴A(-3,0),B(1,0).
(2)当y=5时,x2+2x-3=5,x2+2x-8=0,解得x1=-4,x2=2.
由函数图象可得,当-413.D [解析]
如图,当y=0时,-x2+x+6=0,解得x1=-2,x2=3,则A(-2,0),B(3,0).
将该二次函数图象在x轴上方的部分沿x轴翻折到x轴下方,该部分图象的解析式为y=(x+2)(x-3),即y=x2-x-6(-2≤x≤3).
当直线y=-x+m经过点A(-2,0)时,2+m=0,解得m=-2;
当直线y=-x+m与抛物线y=x2-x-6有唯一公共点时,方程x2-x-6=-x+m有两个相等的实数根,解得m=-6.
所以当直线y=-x+m与新图象有4个公共点时,m的取值范围为-614.C [解析]
如图.
∵抛物线y=x2-7x+与x轴交于点A,B,∴B(5,0),A(9,0),
∴抛物线C1向左平移4个单位长度得到C2,∴平移后抛物线的解析式为y=(x-3)2-2.
当直线y=x+m过点B时,直线y=x+m与C1,C2有2个公共点,
∴0=+m,解得m=-;
当直线y=x+m与抛物线C2只有一个公共点时,令x+m=(x-3)2-2,∴x2-7x+5-2m=0,
∴Δ=49-20+8m=0,∴m=-,此时直线的解析式为y=x-,它与x轴的交点为,0,在点A的左侧,∴此时直线与C1,C2有2个公共点,如图所示.∴当直线y=x+m与C1,C2共有3个不同的公共点时,-15.解:(1)证明:∵a≠0,∴Δ=(-6a)2-4a·5a=16a2>0,故当a为任意非零常数时,抛物线C与x轴总有两个不同的公共点.
(2)对于y=ax2-6ax+5a,令y=0,则x=1或x=5.
令x=0,则y=5a.假设点A在点B的左侧,
则点A,B,D的坐标分别为(1,0),(5,0),(0,5a),
∴△ABD的面积=AB·|yD|=×4×5|a|=20.
解得a=±2.
(3)a的取值范围为-≤a≤-1.
[解析]
①当a>0时,如图①,EF与抛物线不可能有公共点;
②当a<0时,如图②,
临界点为点E,F,
当抛物线过点E,即x=2时,y=4a-12a+5a=-3a=4,解得a=-,
当抛物线过点F,即x=3时,y=9a-18a+5a=-4a=4,解得a=-1,
故a的取值范围为-≤a≤-1.
知识点
1 实际背景的二次函数与一元二次方程
1.从地面竖直向上抛出一个小球,小球的上升高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为h=24t-4t2,那么小球从抛出至回落到地面所需的时间是
( )
A.6
s
B.4
s
C.3
s
D.2
s
2.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t-t2,在飞机着陆滑行中,最后2
s滑行的距离是 m.?
3.如图22-2-1是某公园一喷水池,在水池中央有一垂直于地面的喷水柱,喷水时,水流在各方向沿形状相同的抛物线落下.若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25.
(1)求喷出的水流离地面的最大高度;
(2)求喷嘴离地面的高度;
(3)若把喷水池改成圆形,则水池半径至少为多少时,才能使喷出的水流不落在水池外?
图22-2-1
知识点
2 抛物线与坐标轴的公共点个数与一元二次方程根的个数
4.二次函数y=x2-2x-2的图象与坐标轴的公共点个数是
( )
A.0
B.1
C.2
D.3
5.根据下列表格中的数值,判断方程ax2+bx+c=0(a,b为常数)根的情况是
( )
x
…
-1
0
1
2
3
…
ax2+bx+c
…
-3
2
3
0
-7
…
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.无实数根
6.若函数y=x2-2x+b的图象与坐标轴有三个公共点,则b的取值范围是
( )
A.b<1且b≠0
B.b>1
C.0
7.已知关于x的函数y=(m-1)x2+2x+m的图象与坐标轴只有2个公共点,则m=
.?
8.已知二次函数y=kx2-6x-9的图象与x轴有两个不同的公共点,则k的取值范围为
.?
9.二次函数y=ax2+bx+c的图象如图22-2-2所示,若方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为
.?
图22-2-2
知识点
3 用图象法估计一元二次方程的根
10.根据下列表格中的对应值,判断方程ax2+bx+c=0(a≠0)的一个根x的取值范围是
( )
x
1.23
1.24
1.25
1.26
ax2+bx+c
-0.07
-0.01
0.04
0.08
A.1.23
4 利用图象解一元二次不等式
11.若A(-1,0)为抛物线y=-3(x-1)2+c上一点,则当y≥0时,x的取值范围是
( )
A.-1
C.-1≤x≤3
D.x≤-1或x≥3
12.如图22-2-3,已知抛物线y=x2+2x-3与x轴的两个公共点分别是A,B(点A在点B的左侧).
(1)点A的坐标为 ,点B的坐标为 ;?
(2)利用函数图象,求得当y<5时x的取值范围为 .?
图22-2-3
能力拓展提升
13.已知二次函数y=-x2+x+6及一次函数y=-x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数图象(如图22-2-4所示),当直线y=-x+m与新图象有4个公共点时,m的取值范围是
( )
图22-2-4
A.-
( )
图22-2-5
A.-
(1)求证:当a为任意非零常数时,抛物线C与x轴总有两个不同的公共点;
(2)设抛物线C交x轴于点A,B,交y轴于点D,若△ABD的面积为20,求a的值;
(3)设点E(2,4),F(3,4),若抛物线C与线段EF只有一个公共点,结合函数图象,直接写出a的取值范围.
典题讲评与答案详析
1.A
2.6 [解析]
当y取得最大值时,飞机停下来,
则y=60t-t2=-(t-20)2+600,
此时t=20,飞机着陆后滑行600
m停下来,
因此t的取值范围是0≤t≤20.
当t=18时,y=594,
所以在飞机着陆滑行中,最后2
s滑行的距离是600-594=6(m).
故答案是6.
3.解:(1)∵水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y=-(x-1)2+2.25,
∴喷出的水流离地面的最大高度为2.25
m.
(2)当x=0时,y=-(0-1)2+2.25=1.25,
∴喷嘴离地面的高度为1.25
m.
(3)由题意可得y=0时,0=-(x-1)2+2.25,
解得x1=-0.5(舍去),x2=2.5.
故当水池半径至少为2.5
m时,才能使喷出的水流不落在水池外.
4.D
5.A [解析]
当x=2时,方程ax2+bx+c=0,因此方程有一个实数根为2.当x由-1增大到0时,ax2+bx+c的值由-3增大到2,因此可以推断当x在-1与0之间取某一值时,必有ax2+bx+c=0,说明方程ax2+bx+c=0必有一个根在-1与0之间.
6.A [解析]
∵函数y=x2-2x+b的图象与坐标轴有三个公共点,∴解得b<1且b≠0.
7.1或0或 [解析]
分类讨论:(1)当m-1=0时,m=1,此时函数为一次函数,解析式为y=2x+1,它的图象与x轴的公共点坐标为-,0,与y轴的公共点坐标为(0,1).符合题意.
(2)当m-1≠0时,m≠1,此时函数为二次函数,分两种情况:①图象过原点,且与x轴有两个不同的公共点,于是Δ=4-4(m-1)m>0,解得
9.k<2 [解析]
从图象上来看,当k<2时,抛物线y=ax2+bx+c与直线y=k有两个不同的公共点,此时方程ax2+bx+c=k有两个不相等的实数根.
10.B 11.C
12.(1)(-3,0) (1,0) (2)-4
(1)当x2+2x-3=0时,解得x1=-3,x2=1,∴A(-3,0),B(1,0).
(2)当y=5时,x2+2x-3=5,x2+2x-8=0,解得x1=-4,x2=2.
由函数图象可得,当-4
如图,当y=0时,-x2+x+6=0,解得x1=-2,x2=3,则A(-2,0),B(3,0).
将该二次函数图象在x轴上方的部分沿x轴翻折到x轴下方,该部分图象的解析式为y=(x+2)(x-3),即y=x2-x-6(-2≤x≤3).
当直线y=-x+m经过点A(-2,0)时,2+m=0,解得m=-2;
当直线y=-x+m与抛物线y=x2-x-6有唯一公共点时,方程x2-x-6=-x+m有两个相等的实数根,解得m=-6.
所以当直线y=-x+m与新图象有4个公共点时,m的取值范围为-6
如图.
∵抛物线y=x2-7x+与x轴交于点A,B,∴B(5,0),A(9,0),
∴抛物线C1向左平移4个单位长度得到C2,∴平移后抛物线的解析式为y=(x-3)2-2.
当直线y=x+m过点B时,直线y=x+m与C1,C2有2个公共点,
∴0=+m,解得m=-;
当直线y=x+m与抛物线C2只有一个公共点时,令x+m=(x-3)2-2,∴x2-7x+5-2m=0,
∴Δ=49-20+8m=0,∴m=-,此时直线的解析式为y=x-,它与x轴的交点为,0,在点A的左侧,∴此时直线与C1,C2有2个公共点,如图所示.∴当直线y=x+m与C1,C2共有3个不同的公共点时,-
(2)对于y=ax2-6ax+5a,令y=0,则x=1或x=5.
令x=0,则y=5a.假设点A在点B的左侧,
则点A,B,D的坐标分别为(1,0),(5,0),(0,5a),
∴△ABD的面积=AB·|yD|=×4×5|a|=20.
解得a=±2.
(3)a的取值范围为-≤a≤-1.
[解析]
①当a>0时,如图①,EF与抛物线不可能有公共点;
②当a<0时,如图②,
临界点为点E,F,
当抛物线过点E,即x=2时,y=4a-12a+5a=-3a=4,解得a=-,
当抛物线过点F,即x=3时,y=9a-18a+5a=-4a=4,解得a=-1,
故a的取值范围为-≤a≤-1.
同课章节目录
