2.1 简谐运动课后练习—【新教材】人教版(2019)高中物理选择性必修第一册word版含答案
文档属性
| 名称 | 2.1 简谐运动课后练习—【新教材】人教版(2019)高中物理选择性必修第一册word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 154.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-06-07 07:33:20 | ||
图片预览




文档简介
1简谐运动课后练习
一、单选题
1.做简谐运动的质点通过平衡位置时,具有最大值的物理量是(??
)
A.?加速度??????????????????????????????????B.?速度??????????????????????????????????C.?位移??????????????????????????????????D.?回复力
2.弹簧振子周期为2s,从振子通过平衡位置向右运动起,经过1.8s时,其运动情况是( )
A.?向右减速???????????????????????????B.?向右加速???????????????????????????C.?向左减速???????????????????????????D.?向左加速
3.如图所示,轻弹簧上端固定,下端连接一小物块,物块沿竖直方向做简谐运动。以竖直向上为正方向,物块做简谐运动的表达式为y=0.1sin5πt(m)。t=0时刻,一小球从距物块h
高处自由落下,t=0.3s时,小球恰好与物块处于同一高度,重力加速度g取10m/s2
,
空气阻力不计,
以下判断正确的是(??
)
A.?h=0.35
m???????????????????????????????????????????????????????????
B.?简谐运动的周期是
0.2
s
C.?0.3
s
内物块运动的路程是
0.1
m?????????????????????????D.?t=0.35s
时,物块与小球运动方向相同
4.如图所示,质量为M的物块钩在水平放置的左端固定的轻质弹簧的右端,构成一弹簧振子,物块可沿光滑水平面在BC间做简谐运动,振幅为A.在运动过程中将一质量为m的小物块轻轻地放在M上,第一次是当M运动到平衡位置O处时放在上面,第二次是当M运动到最大位移处C处时放在上面,观察到第一次放后的振幅为A1
,
第二次放后的振幅为A2
,
则(????
)
A.?A1=A2=A?????????????????????????B.?A15.如图所示,一弹簧振子做等幅振动,取向右为正,A、B两处为最大位移处,O为平衡位置,C为AO间某一位置,则振子(??
)
A.?从B→O时,位移是正值,加速度为正值?????????????B.?从O→B时,位移是正值,速度为正值
C.?运动至C处时,位移为负值,加速度为负值?????????D.?运动至C处时,位移为正值,加速度为负值
6.如图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动,取向右为正方向,振子的位移x随时间t的变化如图乙所示,下列说法正确的是(??
)
A.?t=0.2
s时,振子在O点右侧6
cm处
B.?t=0.8
s时,振子的速度方向向左
C.?t=0.4
s和t=1.2
s时,振子的加速度完全相同
D.?t=0.4
s到t=0.8
s的时间内,振子的速度逐渐减小
7.如图所示为波沿着一条固定的绳子向右刚好传播到B点时的波形,由图可判断出A点刚开始振动的方向是(??
)
A.?向左?????????????????????????????????????B.?向右?????????????????????????????????????C.?向下?????????????????????????????????????D.?向上
8.一质点做简谐振动,从平衡位置运动到最远点需要
14
周期,则从平衡位置走过该距离的一半所需时间为(
??)
A.?1/8周期????????????????????????????B.?1/6周期????????????????????????????C.?1/10周期????????????????????????????D.?1/12周期
9.如图所示,将弹簧振子从平衡位置拉下一段距离
Δx
,释放后振子在AB间振动。设AB=20cm,振子由A到B时间为0.1s,则下列说法正确的是(??
)
A.?振子的振幅为20cm,周期为0.2s
B.?振子在A,B两处受到的回复力分别为
kΔx+mg
与
kΔx?mg
C.?振子在A,B两处受到的回复力大小都是
kΔx
D.?振子一次全振动通过的路程是20cm
10.有一个在光滑水平面内的弹簧振子,第一次用力把弹簧压缩x后释放让它振动,第二次把弹簧压缩2x后释放让它振动,则先后两次振动的周期之比和振幅之比分别为(??
)
A.?1∶1??
1∶1???????????????????????B.?1∶1??
1∶2???????????????????????C.?1∶4??
1∶4???????????????????????D.?1∶2??
1∶2
11.如图所示,两根完全相同的弹簧和一根张紧的细线将甲、乙两物块束缚在光滑水平面上,已知甲的质量大于乙的质量.当细线突然断开后,两物块都开始做简谐运动,在运动过程中(??
).
A.?甲的振幅大于乙的振幅
B.?甲的振幅小于乙的振幅
C.?甲的最大速度小于乙的最大速度
D.?甲的最大速度大于乙的最大速度
12.如图所示,AB用一轻弹簧连接,静止在水平地面上,AB的质量均为m,对A施加一竖直向下的力F,力F的大小等于
mg.
现撤去F,A做简谐振动,则A运动到最高点时,B对地面的压力为(??
)
A.?0??????????????????????????????????????B.?mg??????????????????????????????????????C.?2
mg??????????????????????????????????????D.?3
mg
13.下列关于简谐振动和简谐机械波的说法正确的是(???
)
A.?简谐振动的平衡位置一定是物体所受合外力为零的位置。
B.?横波在介质中的传播速度由波源本身的性质决定。
C.?当人向一个固定的声源跑去,人听到的音调变低了。
D.?当声波从空气进入水中时,声波的频率不变,波长变长。
14.把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它的平衡位置为O,在A、B间振动,如图所示,下列结论正确的是(??
).
A.小球在O位置时,动能最大,加速度最小????????????
B.?小球在A,B位置时,动能最大,加速度最大
C.?小球从A经O到B的过程中,回复力一直做正功????
D.?小球从A经O到B的过程中,回复力一直做负功
15.一弹簧振子的位移y随时间t变化的关系式为
y=0.1sin(2.5πt)
,位移y的单位为m,时间t的单位为s。则(??
)
A.?弹簧振子的振幅为0.2m??????????????????????????????????????
B.?弹簧振子的周期为1.25s
C.?在t=0.2s时,振子的运动速度为零??????????????????????D.?在任意0.2s时间内,振子的位移均为0.1m
二、填空题
16.如图所示,?
质量为m的木块放在弹簧上端,
在竖起方向上做简谐运动,当振幅为A时,物体对弹簧的最大压力是物体重力的1.5倍,则物体对弹簧的最小压力是________,
欲使物体在弹簧振动中不离开弹簧,其振幅不能超过________。
17.某同学在进行研究弹簧振子的周期和小球质量的关系的实验时,利用如图甲所示装置进行了如下实验:让弹簧振子穿过一光滑的水平横杆,在弹簧振子的小球上安装一支笔,下面放一条纸带.当小球振动时,垂直于振动方向以恒定的加速度拉动纸带,加速度大小为a,这时笔在纸带上画出如图乙所示的一条曲线,请根据图乙中所测得的长度s1
,
s2
,
写出计算弹簧振子的周期的表达式:T=________.
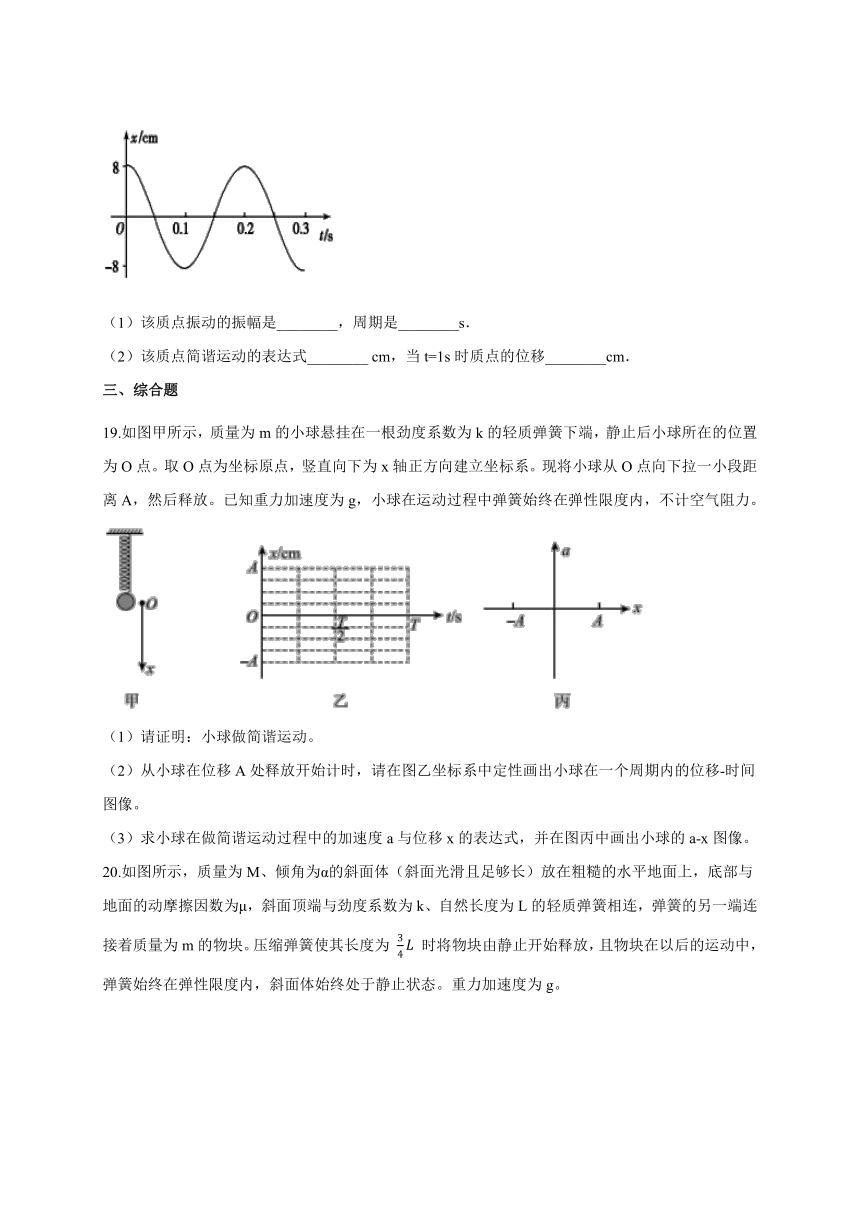
18.一质点简谐运动的振动图象如图所示.
(1)该质点振动的振幅是________,周期是________s.
(2)该质点简谐运动的表达式________
cm,当t=1s时质点的位移________cm.
三、综合题
19.如图甲所示,质量为m的小球悬挂在一根劲度系数为k的轻质弹簧下端,静止后小球所在的位置为O点。取O点为坐标原点,竖直向下为x轴正方向建立坐标系。现将小球从O点向下拉一小段距离A,然后释放。已知重力加速度为g,小球在运动过程中弹簧始终在弹性限度内,不计空气阻力。
(1)请证明:小球做简谐运动。
(2)从小球在位移A处释放开始计时,请在图乙坐标系中定性画出小球在一个周期内的位移-时间图像。
(3)求小球在做简谐运动过程中的加速度a与位移x的表达式,并在图丙中画出小球的a-x图像。
20.如图所示,质量为M、倾角为α的斜面体(斜面光滑且足够长)放在粗糙的水平地面上,底部与地面的动摩擦因数为μ,斜面顶端与劲度系数为k、自然长度为L的轻质弹簧相连,弹簧的另一端连接着质量为m的物块。压缩弹簧使其长度为
34L
时将物块由静止开始释放,且物块在以后的运动中,弹簧始终在弹性限度内,斜面体始终处于静止状态。重力加速度为g。
(1)求物块处于平衡位置时弹簧的长度;
(2)求弹簧的最大伸长量;
(3)为使斜面体始终处于静止状态,动摩擦因数μ应满足什么条件。(假设滑动摩擦力等于最大静摩擦力)
21.弹簧振子以O点为平衡位置,在B、C两点间做简谐运动,在t=0时刻,振子从O、B间的P点以速度v向B点运动;在t=0.20s时,振子速度第一次变为-v;在t=0.60s时,振子速度再变为v,求
(1)求弹簧振子振动周期T,
(2)若B、C之间的距离为20cm,求振子在4.00s内通过的路程,
(3)若B、C之间的距离为20cm,取从O向B为正方向,振子从平衡位置向C运动开始计时,写出弹簧振子位移表达式,并画出弹簧振子的振动图象。
答案解析
一、单选题
1.
B
做简谐运动的质点,当它通过平衡位置时位移为零,简谐运动中的回复力F=-Kx,则回复力等于0,加速度与位移关系为:a=-kx/m,则加速度为0,平衡位置时速度最大。
故答案为:B。
2.
B
由简谐运动的周期性可知,经1.8s时,振子振动时间
t=1.5s+0.3s=34T+0.3s
所以振子正在向右运动,而且是向平衡位置运动,是加速运动,B符合题意,A、C、D不符合题意;
故答案为:B。
3.
A
A.由振动方程式可得,
t=0.3s
物体的位移为
y=0.1sin(5π×0.3)m=?0.1m
则对小球有
?+|y|=12gt2
得到
?=0.35m
A符合题意;
B.由公式
y=0.1sin5πt(m)
可知,简谐运动的周期为
T=2πω=2π5πs=0.4s
B不符合题意;
C.由题可知振幅为
A=0.1m
故0.3s内物块运动的路程为
3A=0.3m
C不符合题意;
D.由于
34T,此时物体在平衡位置下侧,并向上即向平衡位置振动,则此时物块与小球运动方向相反,D不符合题意。
故答案为:A。
4.
B
根据两种情况下系统能量变化的角度分析振幅的变化情况
振子运动到C点时速度恰为0,此时放上小物块,系统的总能量即为此时弹簧储存的弹性势能不变,故振幅不变,即
A2=A
;振子运动到平衡位置时速度最大,弹簧的弹性势能为零,放上小物块后,系统的机械能的减小,根据能量守恒定律可得机械能转化为弹性势能总量减小,故弹簧的最大伸长(压缩)量减小,即振幅减小,所以
A1,故
A1,B符合题意.
故答案为:B
5.
B
A.从B→O时,位移是正值,加速度为负值。A不符合题意;
B.从O→B时,位移是正值,速度为正值。B符合题意;
CD.运动至C处时,位移为负值,加速度为正值。CD不符合题意。
故答案为:B。
6.
B
在0-0.4s内,振子做变减速运动,不是匀速运动,所以t=0.2s时,振子不在O点右侧6cm处,A不符合题意;由图象乙知,t=0.8s时,图象的斜率为负,说明振子的速度为负,即振子的速度方向向左,B符合题意;t=0.4s和
t=1.2s
时,振子的位移完全相反,由
a=?kxm
知加速度完全相反,C不符合题意;t=0.4s到
t=0.8s
的时间内,振子的位移减小,正向平衡位置靠近,速度逐渐增大,D不符合题意。
故答案为:B
7.
D
绳子上向右传播的横波,质点的振动方向与传播方向垂直,不可能沿水平方向.A、B均错误.图示时刻B振动方向向上,则A点刚开始的振动方向向上.C不符合题意,D符合题意.
故答案为:D
8.
D
由简谐振动的表达式有
12x=sin2πTt
,得
2πTt=π6
,
t=112T
,D符合题意.
故答案为:D
9.
C
A.AB间距离为20cm,故振幅为10cm,A不符合题意;
BC.根据F=-kx可知在AB两处回复力大小都为k?x,B不符合题意,C符合题意;
D.振子完成一次全振动经过的路程为40cm,D不符合题意。
故答案为:C。
10.
B
弹簧的压缩量即为振子振动过程中偏离平衡位置的最大距离,即振幅,故振幅之比为1∶2,而对同一振动系统,其周期与振幅无关,则周期之比为1∶1,振动周期由振动系统的性质决定,与振幅无关。
故答案为:B。
11.
C
两根完全相同的弹簧,受到相同的力作用,则伸长量相同,AB不符合题意;当振子速度最大时,弹性势能转化为动能,则质量大的,最大速度小,C符合题意.
故答案为:C
12.
B
施加力F平衡时:
F+mg=kΔx1
撤去力F后,A向上运动受力平衡时:
mg=kΔx2
则简谐运动的振幅为:
d=Δx1?Δx2
弹簧上升到最高点时弹簧的伸长量
Δx=2(Δx1?Δx2)?Δx1=Δx1?2Δx2
弹簧的拉力为:
F′=kΔx
以
mB
为研究对象,设受地面支持力为N:
F′+N=mBg
联立得:
N=mg
根据牛顿第三定律,B对地面的压力大小也等于mg。
故答案为:B
13.
D
AB.单摆运动的平衡位置合外力并不为零,传播速度由介质决定与波源无关,AB不符合题意;
C.当人向一个固定的声源跑去,人听到的音调变高了,C不符合题意;
D.当声波从空气进入水中时,声波的频率不变,波速增大,由
v=λf
知波长变长,D对。
故答案为:D
14.
A
小球在平衡位置时动能最大,加速度为零,因此A符合题意.小球衡位置时,回复力做正功;远离平衡位置时,回复力做负功.振动过程中总能量不变,因此B、C、D不符合题意.
故答案为:A
15.
C
根据公式
x=Asinωt
对应可得,
A=0.1cm
,A不符合题意;根据公式
T=2πω
可得
T=2π2.5π=0.8s
,B不符合题意;在t
=
0.2s时,x=0振子位于正向最大位移处,速度为零,C符合题意;根据振子的振动规律可得,只有振子位于平衡位置或者最大位移处时,经过任意0.2s的时间内的路程为0.1cm,D不符合题意
故答案为:C
二、填空题
16.
0.5mg;2A
当木块运动到最低点时,对弹簧弹力最大,此时由牛顿第二定律得Fmax-mg=ma
因为有Fmax=1.5mg
解得a=0.5g
当木块运动到最高点时,对弹簧弹力最小,此时由牛顿第二定律得mg-Fmin=ma
由运动的对称性知,最高点与最低点的加速度大小相等,即a=0.5g代入求得
Fmin=12mg
在最高点或最低点kA=ma=
12mg
所以弹簧的劲度系数为
k=mg2A
物体在平衡位置下方处于超重状态,不可能离开弹簧,只有在平衡位置上方可能离开弹簧.要使物体在振动过程中恰好不离开弹簧,物体在最高点的加速度a=g此时弹簧的弹力为零.若振幅再大,物体便会脱离弹簧.物体在最高点刚好不离开弹簧时,回复力为重力,所以mg=kA′
则振幅为
A′=mgk=2A
17.
s2?s1a
根据匀变速直线运动的推论公式
Δx=aT2
,有
s2?s1=aT2
,解得
T=s2?s1a
小球做匀变速直线运动公式,结合公式Δx=aT2求解弹簧振子的周期即可。
18.
(1)8cm;0.2
(2)x=8sin(10πt+
π2
);8
解:(1)由图知该质点振动的振幅为
A=8cm;周期为
T=0.2s;(2)角频率ω=
2πT
=
2π0.2
rad/s=10π
rad/s
则质点简谐运动的表达式为
x=Asin(ωt+
π2
)=8sin(10πt+
π2
)cm
当t=1s时,代入上式得:x=8sin(10π×1+
π2
)cm=8cm.
故答案为:(1)8,0.2.(2)x=8sin(10πt+
π2
);8.
三、综合题
19.
(1)解:取竖直向下为正方向.物体静止在O点时kx0=mg
将物体从O点向下拉离的距离为x时,弹簧的弹力大小
k(x0+x)
物体振动的回复力大小为
F=k(x0+x)-mg=kx
回复力方向竖直向下,与位移方向相反,则位移为x时有F=-kx
符合简谐运动的特征,所以物体做简谐运动
(2)解:从小球在位移A处释放开始计时,小球的位移时间图像如图所示
(3)解:由牛顿第二定律可知
a=Fm=?kxm=?kmx
则做出a-x图像如图
(1)利用胡克定律结合平衡条件可以判别小球做简谐运动;
(2)利用小球的简谐运动可以画出对应的图像;
(3)利用牛顿第二定律可以画出加速度和位移的图像。
20.
(1)解:设物块在斜面上平衡时,弹簧伸长量为ΔL,有
mgsinα?kΔL=0
解得
ΔL=mgsinαk
此时弹簧的长度为
L+mgsinαk
(2)解:物块做简谐运动的振幅为
A=L4+mgsinαk
由对称性可知,最大伸长量为
L4+2mgsinαk
(3)解:设物块位移x为正,则斜面体受力情况如图所示,由于斜面体平衡
所以有水平方向
f+FN1sinα?Fcosα=0
竖直方向
FN2?Mg?FN1cosα?Fsinα=0
又
FN1=mgcosα=0
F=k(x+ΔL)联立可得
f=kxcosα
FN2=Mg+mg+kxsinα
为使斜面体始终处于静止状态,结合牛顿第三定律,应有|f|≤μFN2
所以
μ≥|f|fx2=k|x|cosαMg+ng+kxsinα
当x=-A时,上式右端达到最大值,于是有
μ≥(kL+4mgsinα)cosα4Mg+4mgcos2α?kLsinα
(1)利用平衡条件可以求出弹簧的长度;
(2)利用振幅大小可以求出最大的伸长量大小;
(3)利用水平方向和竖直方向的平衡方程结合摩擦力的表达式可以求出动摩擦因素的大小。
21.
(1)解:根据已知条件分析得振子的运动情况如图:
结合运动的对称性可知周期:T=0.6s+(0.6s-0.2s×2)=0.8s
(2)解:若B、C之间的距离为20cm,则A=10cm
在4.0s=5T时间内,振子的路程:x=5×4A=20×10cm=200cm=2.0m
(3)解:若B、C间距离为20cm,则振幅为10cm。从B点开始计时,规定O到B为正方向,则t=0时刻振子从平衡位置向C运动,振子的位移为0,运动的方向为负,则弹簧振子位移表达式为:x=-Acos
2πT
t=-10sin2.5πtcm
振动图象如图所示
(1)根据质点通过B点的速度和时间求解质点振动的周期;
(2)通过质点的周期,结合质点的振幅求解质点走过的位移;
(3)结合质点振动的周期求解振动的角频率,进而求出质点振动的表达式。
一、单选题
1.做简谐运动的质点通过平衡位置时,具有最大值的物理量是(??
)
A.?加速度??????????????????????????????????B.?速度??????????????????????????????????C.?位移??????????????????????????????????D.?回复力
2.弹簧振子周期为2s,从振子通过平衡位置向右运动起,经过1.8s时,其运动情况是( )
A.?向右减速???????????????????????????B.?向右加速???????????????????????????C.?向左减速???????????????????????????D.?向左加速
3.如图所示,轻弹簧上端固定,下端连接一小物块,物块沿竖直方向做简谐运动。以竖直向上为正方向,物块做简谐运动的表达式为y=0.1sin5πt(m)。t=0时刻,一小球从距物块h
高处自由落下,t=0.3s时,小球恰好与物块处于同一高度,重力加速度g取10m/s2
,
空气阻力不计,
以下判断正确的是(??
)
A.?h=0.35
m???????????????????????????????????????????????????????????
B.?简谐运动的周期是
0.2
s
C.?0.3
s
内物块运动的路程是
0.1
m?????????????????????????D.?t=0.35s
时,物块与小球运动方向相同
4.如图所示,质量为M的物块钩在水平放置的左端固定的轻质弹簧的右端,构成一弹簧振子,物块可沿光滑水平面在BC间做简谐运动,振幅为A.在运动过程中将一质量为m的小物块轻轻地放在M上,第一次是当M运动到平衡位置O处时放在上面,第二次是当M运动到最大位移处C处时放在上面,观察到第一次放后的振幅为A1
,
第二次放后的振幅为A2
,
则(????
)
A.?A1=A2=A?????????????????????????B.?A1
)
A.?从B→O时,位移是正值,加速度为正值?????????????B.?从O→B时,位移是正值,速度为正值
C.?运动至C处时,位移为负值,加速度为负值?????????D.?运动至C处时,位移为正值,加速度为负值
6.如图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动,取向右为正方向,振子的位移x随时间t的变化如图乙所示,下列说法正确的是(??
)
A.?t=0.2
s时,振子在O点右侧6
cm处
B.?t=0.8
s时,振子的速度方向向左
C.?t=0.4
s和t=1.2
s时,振子的加速度完全相同
D.?t=0.4
s到t=0.8
s的时间内,振子的速度逐渐减小
7.如图所示为波沿着一条固定的绳子向右刚好传播到B点时的波形,由图可判断出A点刚开始振动的方向是(??
)
A.?向左?????????????????????????????????????B.?向右?????????????????????????????????????C.?向下?????????????????????????????????????D.?向上
8.一质点做简谐振动,从平衡位置运动到最远点需要
14
周期,则从平衡位置走过该距离的一半所需时间为(
??)
A.?1/8周期????????????????????????????B.?1/6周期????????????????????????????C.?1/10周期????????????????????????????D.?1/12周期
9.如图所示,将弹簧振子从平衡位置拉下一段距离
Δx
,释放后振子在AB间振动。设AB=20cm,振子由A到B时间为0.1s,则下列说法正确的是(??
)
A.?振子的振幅为20cm,周期为0.2s
B.?振子在A,B两处受到的回复力分别为
kΔx+mg
与
kΔx?mg
C.?振子在A,B两处受到的回复力大小都是
kΔx
D.?振子一次全振动通过的路程是20cm
10.有一个在光滑水平面内的弹簧振子,第一次用力把弹簧压缩x后释放让它振动,第二次把弹簧压缩2x后释放让它振动,则先后两次振动的周期之比和振幅之比分别为(??
)
A.?1∶1??
1∶1???????????????????????B.?1∶1??
1∶2???????????????????????C.?1∶4??
1∶4???????????????????????D.?1∶2??
1∶2
11.如图所示,两根完全相同的弹簧和一根张紧的细线将甲、乙两物块束缚在光滑水平面上,已知甲的质量大于乙的质量.当细线突然断开后,两物块都开始做简谐运动,在运动过程中(??
).
A.?甲的振幅大于乙的振幅
B.?甲的振幅小于乙的振幅
C.?甲的最大速度小于乙的最大速度
D.?甲的最大速度大于乙的最大速度
12.如图所示,AB用一轻弹簧连接,静止在水平地面上,AB的质量均为m,对A施加一竖直向下的力F,力F的大小等于
mg.
现撤去F,A做简谐振动,则A运动到最高点时,B对地面的压力为(??
)
A.?0??????????????????????????????????????B.?mg??????????????????????????????????????C.?2
mg??????????????????????????????????????D.?3
mg
13.下列关于简谐振动和简谐机械波的说法正确的是(???
)
A.?简谐振动的平衡位置一定是物体所受合外力为零的位置。
B.?横波在介质中的传播速度由波源本身的性质决定。
C.?当人向一个固定的声源跑去,人听到的音调变低了。
D.?当声波从空气进入水中时,声波的频率不变,波长变长。
14.把一个小球套在光滑细杆上,球与轻弹簧相连组成弹簧振子,小球沿杆在水平方向做简谐运动,它的平衡位置为O,在A、B间振动,如图所示,下列结论正确的是(??
).
A.小球在O位置时,动能最大,加速度最小????????????
B.?小球在A,B位置时,动能最大,加速度最大
C.?小球从A经O到B的过程中,回复力一直做正功????
D.?小球从A经O到B的过程中,回复力一直做负功
15.一弹簧振子的位移y随时间t变化的关系式为
y=0.1sin(2.5πt)
,位移y的单位为m,时间t的单位为s。则(??
)
A.?弹簧振子的振幅为0.2m??????????????????????????????????????
B.?弹簧振子的周期为1.25s
C.?在t=0.2s时,振子的运动速度为零??????????????????????D.?在任意0.2s时间内,振子的位移均为0.1m
二、填空题
16.如图所示,?
质量为m的木块放在弹簧上端,
在竖起方向上做简谐运动,当振幅为A时,物体对弹簧的最大压力是物体重力的1.5倍,则物体对弹簧的最小压力是________,
欲使物体在弹簧振动中不离开弹簧,其振幅不能超过________。
17.某同学在进行研究弹簧振子的周期和小球质量的关系的实验时,利用如图甲所示装置进行了如下实验:让弹簧振子穿过一光滑的水平横杆,在弹簧振子的小球上安装一支笔,下面放一条纸带.当小球振动时,垂直于振动方向以恒定的加速度拉动纸带,加速度大小为a,这时笔在纸带上画出如图乙所示的一条曲线,请根据图乙中所测得的长度s1
,
s2
,
写出计算弹簧振子的周期的表达式:T=________.
18.一质点简谐运动的振动图象如图所示.
(1)该质点振动的振幅是________,周期是________s.
(2)该质点简谐运动的表达式________
cm,当t=1s时质点的位移________cm.
三、综合题
19.如图甲所示,质量为m的小球悬挂在一根劲度系数为k的轻质弹簧下端,静止后小球所在的位置为O点。取O点为坐标原点,竖直向下为x轴正方向建立坐标系。现将小球从O点向下拉一小段距离A,然后释放。已知重力加速度为g,小球在运动过程中弹簧始终在弹性限度内,不计空气阻力。
(1)请证明:小球做简谐运动。
(2)从小球在位移A处释放开始计时,请在图乙坐标系中定性画出小球在一个周期内的位移-时间图像。
(3)求小球在做简谐运动过程中的加速度a与位移x的表达式,并在图丙中画出小球的a-x图像。
20.如图所示,质量为M、倾角为α的斜面体(斜面光滑且足够长)放在粗糙的水平地面上,底部与地面的动摩擦因数为μ,斜面顶端与劲度系数为k、自然长度为L的轻质弹簧相连,弹簧的另一端连接着质量为m的物块。压缩弹簧使其长度为
34L
时将物块由静止开始释放,且物块在以后的运动中,弹簧始终在弹性限度内,斜面体始终处于静止状态。重力加速度为g。
(1)求物块处于平衡位置时弹簧的长度;
(2)求弹簧的最大伸长量;
(3)为使斜面体始终处于静止状态,动摩擦因数μ应满足什么条件。(假设滑动摩擦力等于最大静摩擦力)
21.弹簧振子以O点为平衡位置,在B、C两点间做简谐运动,在t=0时刻,振子从O、B间的P点以速度v向B点运动;在t=0.20s时,振子速度第一次变为-v;在t=0.60s时,振子速度再变为v,求
(1)求弹簧振子振动周期T,
(2)若B、C之间的距离为20cm,求振子在4.00s内通过的路程,
(3)若B、C之间的距离为20cm,取从O向B为正方向,振子从平衡位置向C运动开始计时,写出弹簧振子位移表达式,并画出弹簧振子的振动图象。
答案解析
一、单选题
1.
B
做简谐运动的质点,当它通过平衡位置时位移为零,简谐运动中的回复力F=-Kx,则回复力等于0,加速度与位移关系为:a=-kx/m,则加速度为0,平衡位置时速度最大。
故答案为:B。
2.
B
由简谐运动的周期性可知,经1.8s时,振子振动时间
t=1.5s+0.3s=34T+0.3s
所以振子正在向右运动,而且是向平衡位置运动,是加速运动,B符合题意,A、C、D不符合题意;
故答案为:B。
3.
A
A.由振动方程式可得,
t=0.3s
物体的位移为
y=0.1sin(5π×0.3)m=?0.1m
则对小球有
?+|y|=12gt2
得到
?=0.35m
A符合题意;
B.由公式
y=0.1sin5πt(m)
可知,简谐运动的周期为
T=2πω=2π5πs=0.4s
B不符合题意;
C.由题可知振幅为
A=0.1m
故0.3s内物块运动的路程为
3A=0.3m
C不符合题意;
D.由于
34T
故答案为:A。
4.
B
根据两种情况下系统能量变化的角度分析振幅的变化情况
振子运动到C点时速度恰为0,此时放上小物块,系统的总能量即为此时弹簧储存的弹性势能不变,故振幅不变,即
A2=A
;振子运动到平衡位置时速度最大,弹簧的弹性势能为零,放上小物块后,系统的机械能的减小,根据能量守恒定律可得机械能转化为弹性势能总量减小,故弹簧的最大伸长(压缩)量减小,即振幅减小,所以
A1
A1
故答案为:B
5.
B
A.从B→O时,位移是正值,加速度为负值。A不符合题意;
B.从O→B时,位移是正值,速度为正值。B符合题意;
CD.运动至C处时,位移为负值,加速度为正值。CD不符合题意。
故答案为:B。
6.
B
在0-0.4s内,振子做变减速运动,不是匀速运动,所以t=0.2s时,振子不在O点右侧6cm处,A不符合题意;由图象乙知,t=0.8s时,图象的斜率为负,说明振子的速度为负,即振子的速度方向向左,B符合题意;t=0.4s和
t=1.2s
时,振子的位移完全相反,由
a=?kxm
知加速度完全相反,C不符合题意;t=0.4s到
t=0.8s
的时间内,振子的位移减小,正向平衡位置靠近,速度逐渐增大,D不符合题意。
故答案为:B
7.
D
绳子上向右传播的横波,质点的振动方向与传播方向垂直,不可能沿水平方向.A、B均错误.图示时刻B振动方向向上,则A点刚开始的振动方向向上.C不符合题意,D符合题意.
故答案为:D
8.
D
由简谐振动的表达式有
12x=sin2πTt
,得
2πTt=π6
,
t=112T
,D符合题意.
故答案为:D
9.
C
A.AB间距离为20cm,故振幅为10cm,A不符合题意;
BC.根据F=-kx可知在AB两处回复力大小都为k?x,B不符合题意,C符合题意;
D.振子完成一次全振动经过的路程为40cm,D不符合题意。
故答案为:C。
10.
B
弹簧的压缩量即为振子振动过程中偏离平衡位置的最大距离,即振幅,故振幅之比为1∶2,而对同一振动系统,其周期与振幅无关,则周期之比为1∶1,振动周期由振动系统的性质决定,与振幅无关。
故答案为:B。
11.
C
两根完全相同的弹簧,受到相同的力作用,则伸长量相同,AB不符合题意;当振子速度最大时,弹性势能转化为动能,则质量大的,最大速度小,C符合题意.
故答案为:C
12.
B
施加力F平衡时:
F+mg=kΔx1
撤去力F后,A向上运动受力平衡时:
mg=kΔx2
则简谐运动的振幅为:
d=Δx1?Δx2
弹簧上升到最高点时弹簧的伸长量
Δx=2(Δx1?Δx2)?Δx1=Δx1?2Δx2
弹簧的拉力为:
F′=kΔx
以
mB
为研究对象,设受地面支持力为N:
F′+N=mBg
联立得:
N=mg
根据牛顿第三定律,B对地面的压力大小也等于mg。
故答案为:B
13.
D
AB.单摆运动的平衡位置合外力并不为零,传播速度由介质决定与波源无关,AB不符合题意;
C.当人向一个固定的声源跑去,人听到的音调变高了,C不符合题意;
D.当声波从空气进入水中时,声波的频率不变,波速增大,由
v=λf
知波长变长,D对。
故答案为:D
14.
A
小球在平衡位置时动能最大,加速度为零,因此A符合题意.小球衡位置时,回复力做正功;远离平衡位置时,回复力做负功.振动过程中总能量不变,因此B、C、D不符合题意.
故答案为:A
15.
C
根据公式
x=Asinωt
对应可得,
A=0.1cm
,A不符合题意;根据公式
T=2πω
可得
T=2π2.5π=0.8s
,B不符合题意;在t
=
0.2s时,x=0振子位于正向最大位移处,速度为零,C符合题意;根据振子的振动规律可得,只有振子位于平衡位置或者最大位移处时,经过任意0.2s的时间内的路程为0.1cm,D不符合题意
故答案为:C
二、填空题
16.
0.5mg;2A
当木块运动到最低点时,对弹簧弹力最大,此时由牛顿第二定律得Fmax-mg=ma
因为有Fmax=1.5mg
解得a=0.5g
当木块运动到最高点时,对弹簧弹力最小,此时由牛顿第二定律得mg-Fmin=ma
由运动的对称性知,最高点与最低点的加速度大小相等,即a=0.5g代入求得
Fmin=12mg
在最高点或最低点kA=ma=
12mg
所以弹簧的劲度系数为
k=mg2A
物体在平衡位置下方处于超重状态,不可能离开弹簧,只有在平衡位置上方可能离开弹簧.要使物体在振动过程中恰好不离开弹簧,物体在最高点的加速度a=g此时弹簧的弹力为零.若振幅再大,物体便会脱离弹簧.物体在最高点刚好不离开弹簧时,回复力为重力,所以mg=kA′
则振幅为
A′=mgk=2A
17.
s2?s1a
根据匀变速直线运动的推论公式
Δx=aT2
,有
s2?s1=aT2
,解得
T=s2?s1a
小球做匀变速直线运动公式,结合公式Δx=aT2求解弹簧振子的周期即可。
18.
(1)8cm;0.2
(2)x=8sin(10πt+
π2
);8
解:(1)由图知该质点振动的振幅为
A=8cm;周期为
T=0.2s;(2)角频率ω=
2πT
=
2π0.2
rad/s=10π
rad/s
则质点简谐运动的表达式为
x=Asin(ωt+
π2
)=8sin(10πt+
π2
)cm
当t=1s时,代入上式得:x=8sin(10π×1+
π2
)cm=8cm.
故答案为:(1)8,0.2.(2)x=8sin(10πt+
π2
);8.
三、综合题
19.
(1)解:取竖直向下为正方向.物体静止在O点时kx0=mg
将物体从O点向下拉离的距离为x时,弹簧的弹力大小
k(x0+x)
物体振动的回复力大小为
F=k(x0+x)-mg=kx
回复力方向竖直向下,与位移方向相反,则位移为x时有F=-kx
符合简谐运动的特征,所以物体做简谐运动
(2)解:从小球在位移A处释放开始计时,小球的位移时间图像如图所示
(3)解:由牛顿第二定律可知
a=Fm=?kxm=?kmx
则做出a-x图像如图
(1)利用胡克定律结合平衡条件可以判别小球做简谐运动;
(2)利用小球的简谐运动可以画出对应的图像;
(3)利用牛顿第二定律可以画出加速度和位移的图像。
20.
(1)解:设物块在斜面上平衡时,弹簧伸长量为ΔL,有
mgsinα?kΔL=0
解得
ΔL=mgsinαk
此时弹簧的长度为
L+mgsinαk
(2)解:物块做简谐运动的振幅为
A=L4+mgsinαk
由对称性可知,最大伸长量为
L4+2mgsinαk
(3)解:设物块位移x为正,则斜面体受力情况如图所示,由于斜面体平衡
所以有水平方向
f+FN1sinα?Fcosα=0
竖直方向
FN2?Mg?FN1cosα?Fsinα=0
又
FN1=mgcosα=0
F=k(x+ΔL)联立可得
f=kxcosα
FN2=Mg+mg+kxsinα
为使斜面体始终处于静止状态,结合牛顿第三定律,应有|f|≤μFN2
所以
μ≥|f|fx2=k|x|cosαMg+ng+kxsinα
当x=-A时,上式右端达到最大值,于是有
μ≥(kL+4mgsinα)cosα4Mg+4mgcos2α?kLsinα
(1)利用平衡条件可以求出弹簧的长度;
(2)利用振幅大小可以求出最大的伸长量大小;
(3)利用水平方向和竖直方向的平衡方程结合摩擦力的表达式可以求出动摩擦因素的大小。
21.
(1)解:根据已知条件分析得振子的运动情况如图:
结合运动的对称性可知周期:T=0.6s+(0.6s-0.2s×2)=0.8s
(2)解:若B、C之间的距离为20cm,则A=10cm
在4.0s=5T时间内,振子的路程:x=5×4A=20×10cm=200cm=2.0m
(3)解:若B、C间距离为20cm,则振幅为10cm。从B点开始计时,规定O到B为正方向,则t=0时刻振子从平衡位置向C运动,振子的位移为0,运动的方向为负,则弹簧振子位移表达式为:x=-Acos
2πT
t=-10sin2.5πtcm
振动图象如图所示
(1)根据质点通过B点的速度和时间求解质点振动的周期;
(2)通过质点的周期,结合质点的振幅求解质点走过的位移;
(3)结合质点振动的周期求解振动的角频率,进而求出质点振动的表达式。
