七年级数学镶嵌
图片预览







文档简介
(共39张PPT)
乐昌市新时代学校 曾月权
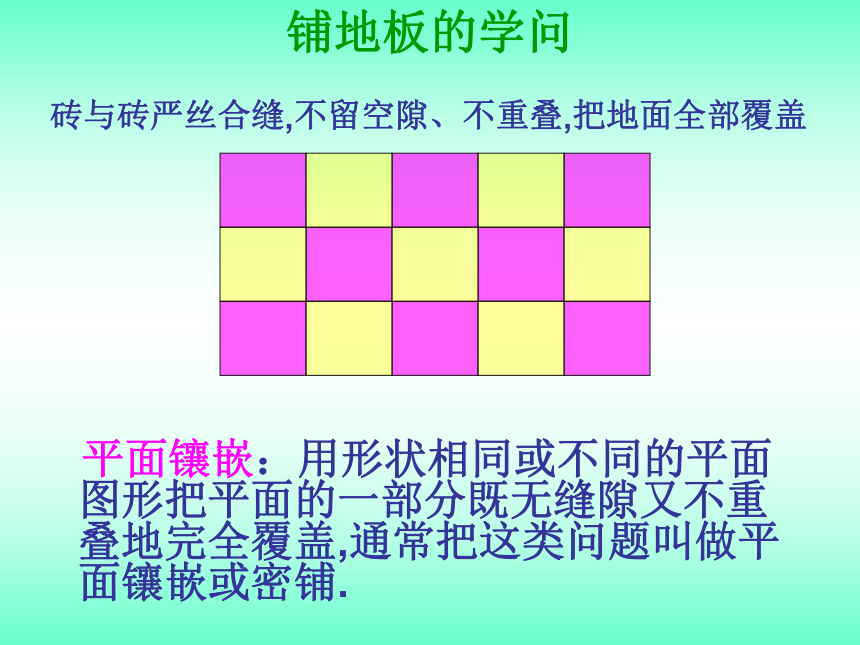
铺地板的学问
平面镶嵌:用形状相同或不同的平面图形把平面的一部分既无缝隙又不重叠地完全覆盖,通常把这类问题叫做平面镶嵌或密铺.
砖与砖严丝合缝,不留空隙、不重叠,把地面全部覆盖
探究1:仅用一种正多边形进行镶嵌,哪些正多边形能单独镶嵌呢?
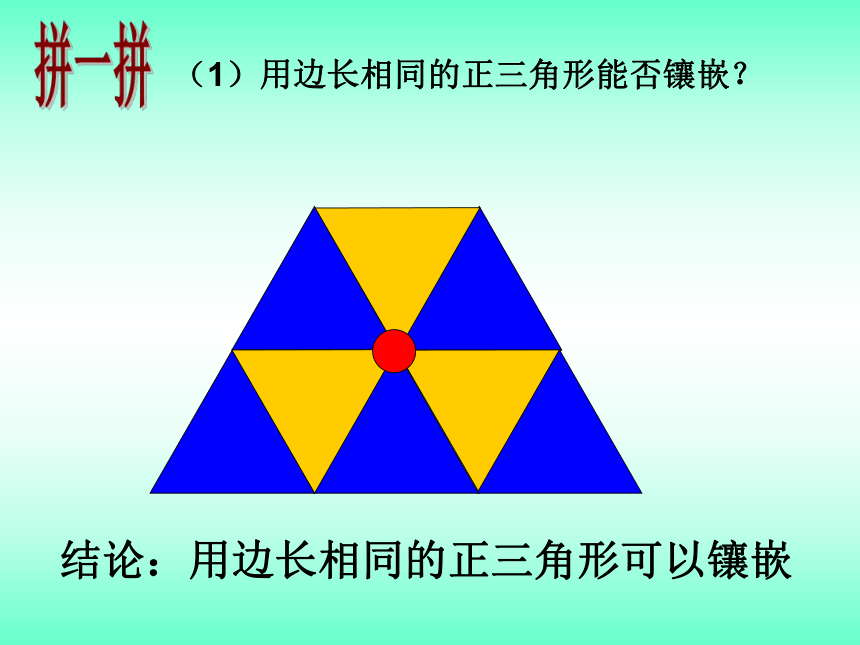
(1)用边长相同的正三角形能否镶嵌?
结论:用边长相同的正三角形可以镶嵌
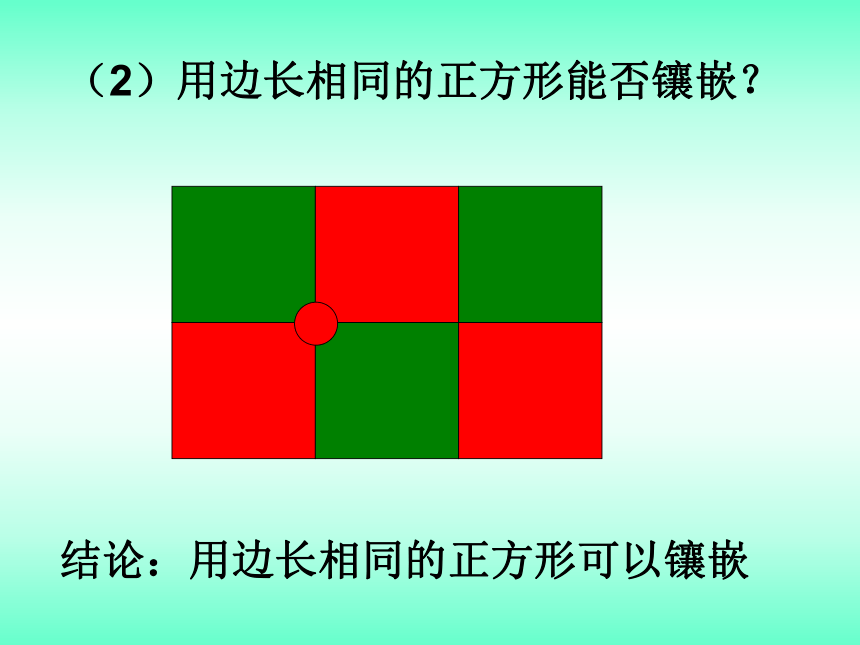
(2)用边长相同的正方形能否镶嵌?
结论:用边长相同的正方形可以镶嵌
(3)用边长相同的正六边形能否镶嵌?
结论:用边长相同的正六边形可以镶嵌
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
(4)用边长相同的正五边形能否镶嵌?
理一理
6
60
0
90
0
108
0
120
0
4
3
3
能拼好
能拼好
不能拼好
有缺口
能拼好
60 ×6=360
0
0
90 ×4=360
0
0
108 ×3<360
0
0
120 ×3=360
0
0
实 验 结 果
正n边形
拼图
每个内角度数
多边形个数
结果
n = 3
n = 4
n =5
n = 6
结论:
可以用同一种正多边形镶嵌的图形只有正三角形,正四边形,正六边形.
探究2:用边长相等的两种正多边形进行镶嵌,哪两种正多边形能镶嵌呢?
60°×3+90°×2=360°
60°×4 + 120°=360°
60°×2+120°×2=360°
正方形和正六边形不能镶嵌
讨 论
正三角形和正方形能镶嵌
正三角形和正六边形能镶嵌
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
用两种正多边形进行镶嵌应满足什么条件 ?
当围绕一点拼在一起的两种正多边形的内角和恰好是360°时,这两种正多边形就能镶嵌.
结论:
探究3:
用几个形状、大小相同的任意三角形能镶嵌吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
结论:相同的任意三角形能平面镶嵌。
1
3
2
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以相同的任意四边形能平面镶嵌。
结论:
用一种形状、大小完全相同的三角形,四边形也能进行平面镶嵌。
4、下列正多边形的组合中 , 不能镶嵌的是 ( ) A. 正方形和正三角形 B. 正方形和正八边形 C. 正三角形和正十二边形 D. 正方形和正六边形
1、下列正多边形不能平面镶嵌的是 ( ) A .正三角形 B. 正方形 C. 正五边形 D .正六边形
2、用正方形一种图形进行平面镶嵌时,在它的一个顶点周围的
正方形的个数是( )
A. 3 B .4 C.5 D .6
3、如果只用一种正多边形作平面镶嵌,而且在每一个正多边形
的每一个顶点周围都有6个正多边形,则该正多边形的内角度数
为( )
A.120 0 B.90 0 C.60 0 D.450
练习:
C
C
B
D
发现二:
用两种正多边形能进行平面镶嵌的条件:1.拼接在同一点
的各个角的度数和是360°;2.相邻的多边形有公共边。
发现一:
用同一种正多边形能进行平面镶嵌的图形只有三种:正三
角形、正方形、正六边形。
通过这堂课的学习,你有什么收获和发现?
发现三:
用一种形状、大小完全相同的三角形,四边形也能进行平
面镶嵌。
课后探究题:(任选一题)
(1)设计一幅平面图形铺满地面的图案,与同学比一比,看看谁设计得更美丽、更有创意。
(2)试以“瓷砖中的数学知识”为题,写一篇小论文。
乐昌市新时代学校 曾月权
铺地板的学问
平面镶嵌:用形状相同或不同的平面图形把平面的一部分既无缝隙又不重叠地完全覆盖,通常把这类问题叫做平面镶嵌或密铺.
砖与砖严丝合缝,不留空隙、不重叠,把地面全部覆盖
探究1:仅用一种正多边形进行镶嵌,哪些正多边形能单独镶嵌呢?
(1)用边长相同的正三角形能否镶嵌?
结论:用边长相同的正三角形可以镶嵌
(2)用边长相同的正方形能否镶嵌?
结论:用边长相同的正方形可以镶嵌
(3)用边长相同的正六边形能否镶嵌?
结论:用边长相同的正六边形可以镶嵌
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
(4)用边长相同的正五边形能否镶嵌?
理一理
6
60
0
90
0
108
0
120
0
4
3
3
能拼好
能拼好
不能拼好
有缺口
能拼好
60 ×6=360
0
0
90 ×4=360
0
0
108 ×3<360
0
0
120 ×3=360
0
0
实 验 结 果
正n边形
拼图
每个内角度数
多边形个数
结果
n = 3
n = 4
n =5
n = 6
结论:
可以用同一种正多边形镶嵌的图形只有正三角形,正四边形,正六边形.
探究2:用边长相等的两种正多边形进行镶嵌,哪两种正多边形能镶嵌呢?
60°×3+90°×2=360°
60°×4 + 120°=360°
60°×2+120°×2=360°
正方形和正六边形不能镶嵌
讨 论
正三角形和正方形能镶嵌
正三角形和正六边形能镶嵌
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
用两种正多边形进行镶嵌应满足什么条件 ?
当围绕一点拼在一起的两种正多边形的内角和恰好是360°时,这两种正多边形就能镶嵌.
结论:
探究3:
用几个形状、大小相同的任意三角形能镶嵌吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
结论:相同的任意三角形能平面镶嵌。
1
3
2
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以相同的任意四边形能平面镶嵌。
结论:
用一种形状、大小完全相同的三角形,四边形也能进行平面镶嵌。
4、下列正多边形的组合中 , 不能镶嵌的是 ( ) A. 正方形和正三角形 B. 正方形和正八边形 C. 正三角形和正十二边形 D. 正方形和正六边形
1、下列正多边形不能平面镶嵌的是 ( ) A .正三角形 B. 正方形 C. 正五边形 D .正六边形
2、用正方形一种图形进行平面镶嵌时,在它的一个顶点周围的
正方形的个数是( )
A. 3 B .4 C.5 D .6
3、如果只用一种正多边形作平面镶嵌,而且在每一个正多边形
的每一个顶点周围都有6个正多边形,则该正多边形的内角度数
为( )
A.120 0 B.90 0 C.60 0 D.450
练习:
C
C
B
D
发现二:
用两种正多边形能进行平面镶嵌的条件:1.拼接在同一点
的各个角的度数和是360°;2.相邻的多边形有公共边。
发现一:
用同一种正多边形能进行平面镶嵌的图形只有三种:正三
角形、正方形、正六边形。
通过这堂课的学习,你有什么收获和发现?
发现三:
用一种形状、大小完全相同的三角形,四边形也能进行平
面镶嵌。
课后探究题:(任选一题)
(1)设计一幅平面图形铺满地面的图案,与同学比一比,看看谁设计得更美丽、更有创意。
(2)试以“瓷砖中的数学知识”为题,写一篇小论文。
