2021—2022学年人教版数学九年级上册24.2.1 点和圆的位置关系同步练习(word解析版)
文档属性
| 名称 | 2021—2022学年人教版数学九年级上册24.2.1 点和圆的位置关系同步练习(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 253.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 12:43:14 | ||
图片预览


文档简介
24.2.1 点和圆的位置关系
知识点
1 由数量关系判断点与圆的位置关系
1.[2020·江阴期中]
已知点A与☉O在同一平面内,☉O的半径是4,且点A到圆心O的距离是3,则点A与☉O的位置关系是
( )
A.点A在☉O外
B.点A在☉O内
C.点A在☉O上
D.不能确定
2.如图24-2-1,在矩形ABCD中,AB=3,AD=4.若以点A为圆心,4为半径作☉A,则下列各点中在☉A外的是
( )
图24-2-1
A.点A
B.点B
C.点C
D.点D
3.[2020·无锡期中]
已知☉O的半径为1,AO=d,且关于x的方程x2-2dx+1=0有两个相等的实数根,则点A与☉O的位置关系是
( )
A.点A在☉O内
B.点A在☉O外
C.点A在☉O上
D.无法确定
4.如图24-2-2,城市A的正北方向50千米的B处,有一无线电信号发射塔.已知该发射塔发射的无线电信号的有效半径为100千米,AC是一条直达C城的公路,从A城发往C城的班车速度为60千米/时.
(1)当班车从A城出发开往C城时,某人立即打开无线电收音机,班车行驶了0.5小时的时候,接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
(2)班车从A城到C城共行驶2小时,请你判断到C城后还能不能接收到信号,并说明理由.
图24-2-2
知识点
2 由点与圆的位置关系判断数量关系
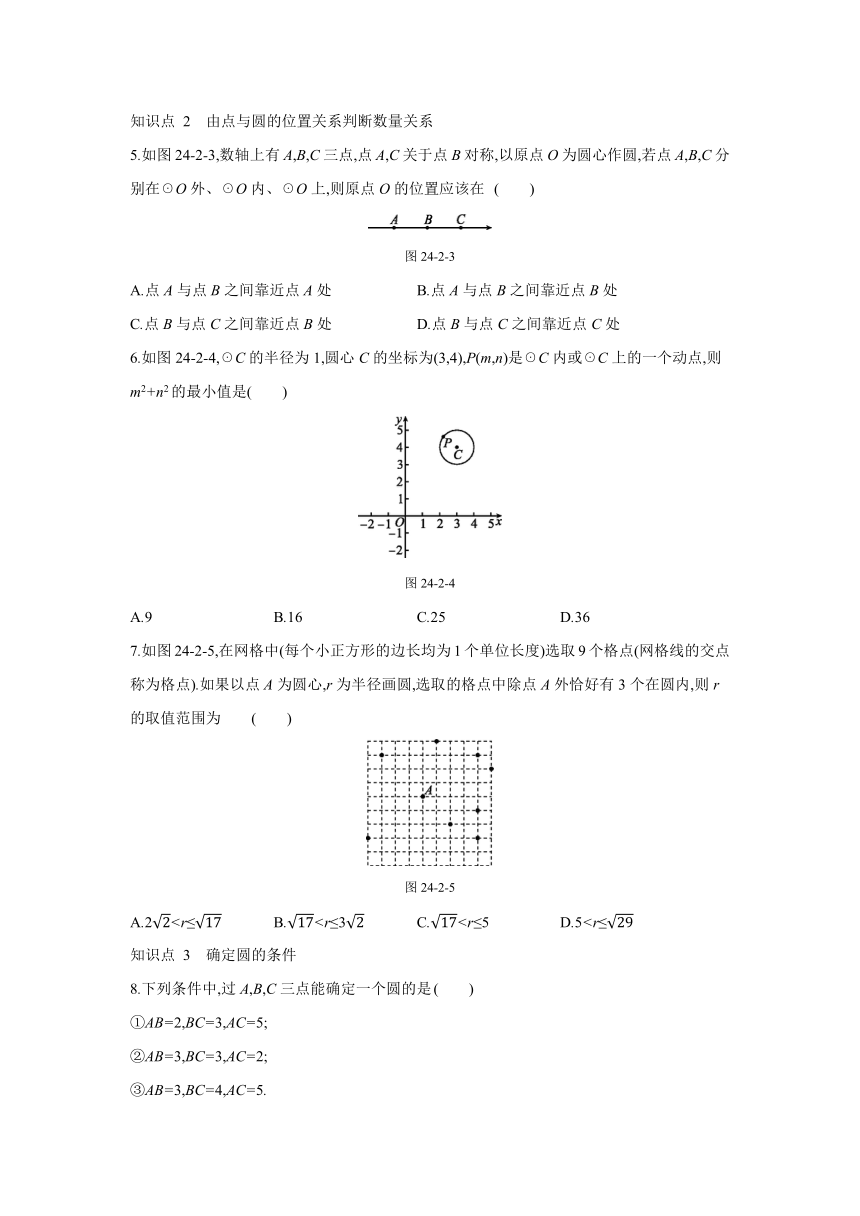
5.如图24-2-3,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在☉O外、☉O内、☉O上,则原点O的位置应该在
( )
图24-2-3
A.点A与点B之间靠近点A处
B.点A与点B之间靠近点B处
C.点B与点C之间靠近点B处
D.点B与点C之间靠近点C处
6.如图24-2-4,☉C的半径为1,圆心C的坐标为(3,4),P(m,n)是☉C内或☉C上的一个动点,则m2+n2的最小值是( )
图24-2-4
A.9
B.16
C.25
D.36
7.如图24-2-5,在网格中(每个小正方形的边长均为1个单位长度)选取9个格点(网格线的交点称为格点).如果以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为
( )
图24-2-5
A.2B.C.D.5知识点
3 确定圆的条件
8.下列条件中,过A,B,C三点能确定一个圆的是
( )
①AB=2,BC=3,AC=5;
②AB=3,BC=3,AC=2;
③AB=3,BC=4,AC=5.
A.①②
B.①②③
C.②③
D.①③
9.已知A,B,C为平面上的三点,AB=2,BC=3,AC=5,则
( )
A.可以画一个圆,使点A,B,C都在圆周上
B.可以画一个圆,使点A,B在圆周上,点C在圆内
C.可以画一个圆,使点A,C在圆周上,点B在圆外
D.可以画一个圆,使点A,C在圆周上,点B在圆内
命题点
4 三角形的外接圆和外心
10.如图24-2-6,AC,BE是☉O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是
( )
A.△ABE
B.△ACF
C.△ABD
D.△ADE
图24-2-6
图24-2-7
11.[2020·黄石模拟]
如图24-2-7所示,在平面直角坐标系中,A(-2,2),B(8,2),C(6,6),点P为△ABC的外接圆的圆心,将△ABC绕点O逆时针旋转90°,点P的对应点P'的坐标为
( )
A.(-2,3)
B.(-3,2)
C.(2,-3)
D.(3,-2)
12.如图24-2-8,在正三角形网格中,△ABC的顶点都在格点上,点P,Q,M是AB与网格线的交点,则△ABC的外心是
( )
图24-2-8
A.点P
B.点Q
C.点M
D.点N
13.如图24-2-9,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足
∠PAB=∠PBC,则线段CP长的最小值为
( )
图24-2-9
A.
B.2
C.
D.
14.如图24-2-10,已知△ABC的外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向外作等腰直角三角形ABD与等腰直角三角形ACE,连接BE,CD交于点P,连接OP,则OP长的最小值是 .?
图24-2-10
知识点
5 反证法
15.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是
( )
A.点在圆内
B.点在圆上
C.点在圆心上
D.点在圆上或圆内
16.选择用反证法证明“已知:在△ABC中,∠C=90°.求证:∠A,∠B中至少有一个角不大于45°.”时,应先假设
( )
A.∠A>45°,∠B>45°
B.∠A≥45°,∠B≥45°
C.∠A<45°,∠B<45°
D.∠A≤45°,∠B≤45°
能力拓展提升
17.定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图24-2-11,在损矩形ABCD中,∠ABC=∠ADC=90°,则该损矩形的直径是线段 .?
(2)①在损矩形ABCD内是否存在点O,使得A,B,C,D四个点都在以点O为圆心的同一个圆上?如果有,请指出点O的具体位置;
②如图24-2-11,直接写出符合损矩形ABCD的两个结论(不再添加任何线段或点).
图24-2-11
典题讲评与答案详析
1.B 2.C 3.C
4.解:(1)如图,过点B作BM⊥AC于点M,
则班车行驶了0.5小时的时候到达点M.
∵AM=60×0.5=30(千米),AB=50千米,
∴BM==40千米.
答:此时,班车到发射塔的距离是40千米.
(2)能.理由如下:如图,连接BC.
∵AC=60×2=120(千米),AM=30千米,
∴CM=AC-AM=120-30=90(千米),
∴BC===10(千米)<100千米,
∴到C城后还能接收到信号.
5.C [解析]
如图.
6.B [解析]
如图,连接OC交☉C于点P'.
∵圆心C的坐标为(3,4),点P的坐标为(m,n),
∴OC=5,
OP=,
∴m2+n2是点P到原点的距离的平方,
∴当点P运动到点P'处时,点P离原点最近,即m2+n2取得最小值,
此时OP=OC-PC=5-1=4,即m2+n2=16.
7.B
[解析]
如图,∵AD=2
,AE=AF=,AB=3
,
∴AB>AE=AF>AD,
∴当8.C
9.D [解析]
由题意可知A,B,C三点在同一直线上,且点B在点A,C之间,因此过点A,C可以画一个圆,且点B在圆内.
10.B 11.A
12.B [解析]
由题意可知∠BCN=60°,∠ACN=30°,∴∠ACB=∠ACN+∠BCN=90°,
∴△ABC是直角三角形,
∴△ABC的外心是斜边AB的中点.
∵Q是AB的中点,∴△ABC的外心是点Q.
13.B [解析]
∵∠ABC=90°,
∴∠ABP+∠PBC=90°.
∵∠PAB=∠PBC,
∴∠ABP+∠PAB=90°,
∴∠APB=90°,
∴点P在以AB为直径的圆上.设圆心为O,连接OC交☉O于点P,此时CP最小.
在Rt△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC=5,OP=OB=3,∴PC=OC-OP=5-3=2,∴PC的最小值为2.
14.5- [解析]
∵∠BAD=∠CAE=90°,
∴∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE,
从而∠PDB+∠PBD=∠PDB+∠DBA+∠ADC=90°,
即∠DPB=90°,从而∠BPC=90°,
∴点P在以BC为直径的圆上.
如图,过点O作OH⊥BC于点H,连接OB,OC.
∵△ABC的外心为O,∠BAC=60°,
∴∠BOC=120°.又∵BC=10,
∴OH=
,∴OP长的最小值是5-.
15.D 16.A
17.解:(1)AC
(2)①在损矩形ABCD内存在点O,使得A,B,C,D四个点都在以点O为圆心的同一个圆上,O是线段AC的中点.
②答案不唯一,如损矩形ABCD是圆内接四边形,∠ADB=∠ACB等.
知识点
1 由数量关系判断点与圆的位置关系
1.[2020·江阴期中]
已知点A与☉O在同一平面内,☉O的半径是4,且点A到圆心O的距离是3,则点A与☉O的位置关系是
( )
A.点A在☉O外
B.点A在☉O内
C.点A在☉O上
D.不能确定
2.如图24-2-1,在矩形ABCD中,AB=3,AD=4.若以点A为圆心,4为半径作☉A,则下列各点中在☉A外的是
( )
图24-2-1
A.点A
B.点B
C.点C
D.点D
3.[2020·无锡期中]
已知☉O的半径为1,AO=d,且关于x的方程x2-2dx+1=0有两个相等的实数根,则点A与☉O的位置关系是
( )
A.点A在☉O内
B.点A在☉O外
C.点A在☉O上
D.无法确定
4.如图24-2-2,城市A的正北方向50千米的B处,有一无线电信号发射塔.已知该发射塔发射的无线电信号的有效半径为100千米,AC是一条直达C城的公路,从A城发往C城的班车速度为60千米/时.
(1)当班车从A城出发开往C城时,某人立即打开无线电收音机,班车行驶了0.5小时的时候,接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
(2)班车从A城到C城共行驶2小时,请你判断到C城后还能不能接收到信号,并说明理由.
图24-2-2
知识点
2 由点与圆的位置关系判断数量关系
5.如图24-2-3,数轴上有A,B,C三点,点A,C关于点B对称,以原点O为圆心作圆,若点A,B,C分别在☉O外、☉O内、☉O上,则原点O的位置应该在
( )
图24-2-3
A.点A与点B之间靠近点A处
B.点A与点B之间靠近点B处
C.点B与点C之间靠近点B处
D.点B与点C之间靠近点C处
6.如图24-2-4,☉C的半径为1,圆心C的坐标为(3,4),P(m,n)是☉C内或☉C上的一个动点,则m2+n2的最小值是( )
图24-2-4
A.9
B.16
C.25
D.36
7.如图24-2-5,在网格中(每个小正方形的边长均为1个单位长度)选取9个格点(网格线的交点称为格点).如果以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为
( )
图24-2-5
A.2
3 确定圆的条件
8.下列条件中,过A,B,C三点能确定一个圆的是
( )
①AB=2,BC=3,AC=5;
②AB=3,BC=3,AC=2;
③AB=3,BC=4,AC=5.
A.①②
B.①②③
C.②③
D.①③
9.已知A,B,C为平面上的三点,AB=2,BC=3,AC=5,则
( )
A.可以画一个圆,使点A,B,C都在圆周上
B.可以画一个圆,使点A,B在圆周上,点C在圆内
C.可以画一个圆,使点A,C在圆周上,点B在圆外
D.可以画一个圆,使点A,C在圆周上,点B在圆内
命题点
4 三角形的外接圆和外心
10.如图24-2-6,AC,BE是☉O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是
( )
A.△ABE
B.△ACF
C.△ABD
D.△ADE
图24-2-6
图24-2-7
11.[2020·黄石模拟]
如图24-2-7所示,在平面直角坐标系中,A(-2,2),B(8,2),C(6,6),点P为△ABC的外接圆的圆心,将△ABC绕点O逆时针旋转90°,点P的对应点P'的坐标为
( )
A.(-2,3)
B.(-3,2)
C.(2,-3)
D.(3,-2)
12.如图24-2-8,在正三角形网格中,△ABC的顶点都在格点上,点P,Q,M是AB与网格线的交点,则△ABC的外心是
( )
图24-2-8
A.点P
B.点Q
C.点M
D.点N
13.如图24-2-9,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足
∠PAB=∠PBC,则线段CP长的最小值为
( )
图24-2-9
A.
B.2
C.
D.
14.如图24-2-10,已知△ABC的外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向外作等腰直角三角形ABD与等腰直角三角形ACE,连接BE,CD交于点P,连接OP,则OP长的最小值是 .?
图24-2-10
知识点
5 反证法
15.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是
( )
A.点在圆内
B.点在圆上
C.点在圆心上
D.点在圆上或圆内
16.选择用反证法证明“已知:在△ABC中,∠C=90°.求证:∠A,∠B中至少有一个角不大于45°.”时,应先假设
( )
A.∠A>45°,∠B>45°
B.∠A≥45°,∠B≥45°
C.∠A<45°,∠B<45°
D.∠A≤45°,∠B≤45°
能力拓展提升
17.定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图24-2-11,在损矩形ABCD中,∠ABC=∠ADC=90°,则该损矩形的直径是线段 .?
(2)①在损矩形ABCD内是否存在点O,使得A,B,C,D四个点都在以点O为圆心的同一个圆上?如果有,请指出点O的具体位置;
②如图24-2-11,直接写出符合损矩形ABCD的两个结论(不再添加任何线段或点).
图24-2-11
典题讲评与答案详析
1.B 2.C 3.C
4.解:(1)如图,过点B作BM⊥AC于点M,
则班车行驶了0.5小时的时候到达点M.
∵AM=60×0.5=30(千米),AB=50千米,
∴BM==40千米.
答:此时,班车到发射塔的距离是40千米.
(2)能.理由如下:如图,连接BC.
∵AC=60×2=120(千米),AM=30千米,
∴CM=AC-AM=120-30=90(千米),
∴BC===10(千米)<100千米,
∴到C城后还能接收到信号.
5.C [解析]
如图.
6.B [解析]
如图,连接OC交☉C于点P'.
∵圆心C的坐标为(3,4),点P的坐标为(m,n),
∴OC=5,
OP=,
∴m2+n2是点P到原点的距离的平方,
∴当点P运动到点P'处时,点P离原点最近,即m2+n2取得最小值,
此时OP=OC-PC=5-1=4,即m2+n2=16.
7.B
[解析]
如图,∵AD=2
,AE=AF=,AB=3
,
∴AB>AE=AF>AD,
∴当
9.D [解析]
由题意可知A,B,C三点在同一直线上,且点B在点A,C之间,因此过点A,C可以画一个圆,且点B在圆内.
10.B 11.A
12.B [解析]
由题意可知∠BCN=60°,∠ACN=30°,∴∠ACB=∠ACN+∠BCN=90°,
∴△ABC是直角三角形,
∴△ABC的外心是斜边AB的中点.
∵Q是AB的中点,∴△ABC的外心是点Q.
13.B [解析]
∵∠ABC=90°,
∴∠ABP+∠PBC=90°.
∵∠PAB=∠PBC,
∴∠ABP+∠PAB=90°,
∴∠APB=90°,
∴点P在以AB为直径的圆上.设圆心为O,连接OC交☉O于点P,此时CP最小.
在Rt△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC=5,OP=OB=3,∴PC=OC-OP=5-3=2,∴PC的最小值为2.
14.5- [解析]
∵∠BAD=∠CAE=90°,
∴∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE,
从而∠PDB+∠PBD=∠PDB+∠DBA+∠ADC=90°,
即∠DPB=90°,从而∠BPC=90°,
∴点P在以BC为直径的圆上.
如图,过点O作OH⊥BC于点H,连接OB,OC.
∵△ABC的外心为O,∠BAC=60°,
∴∠BOC=120°.又∵BC=10,
∴OH=
,∴OP长的最小值是5-.
15.D 16.A
17.解:(1)AC
(2)①在损矩形ABCD内存在点O,使得A,B,C,D四个点都在以点O为圆心的同一个圆上,O是线段AC的中点.
②答案不唯一,如损矩形ABCD是圆内接四边形,∠ADB=∠ACB等.
同课章节目录
