浙江省衢州市温州市“衢温5+1”联盟2020-2021学年高一下学期期中联考数学试题 Word版含答案
文档属性
| 名称 | 浙江省衢州市温州市“衢温5+1”联盟2020-2021学年高一下学期期中联考数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 462.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 22:13:43 | ||
图片预览

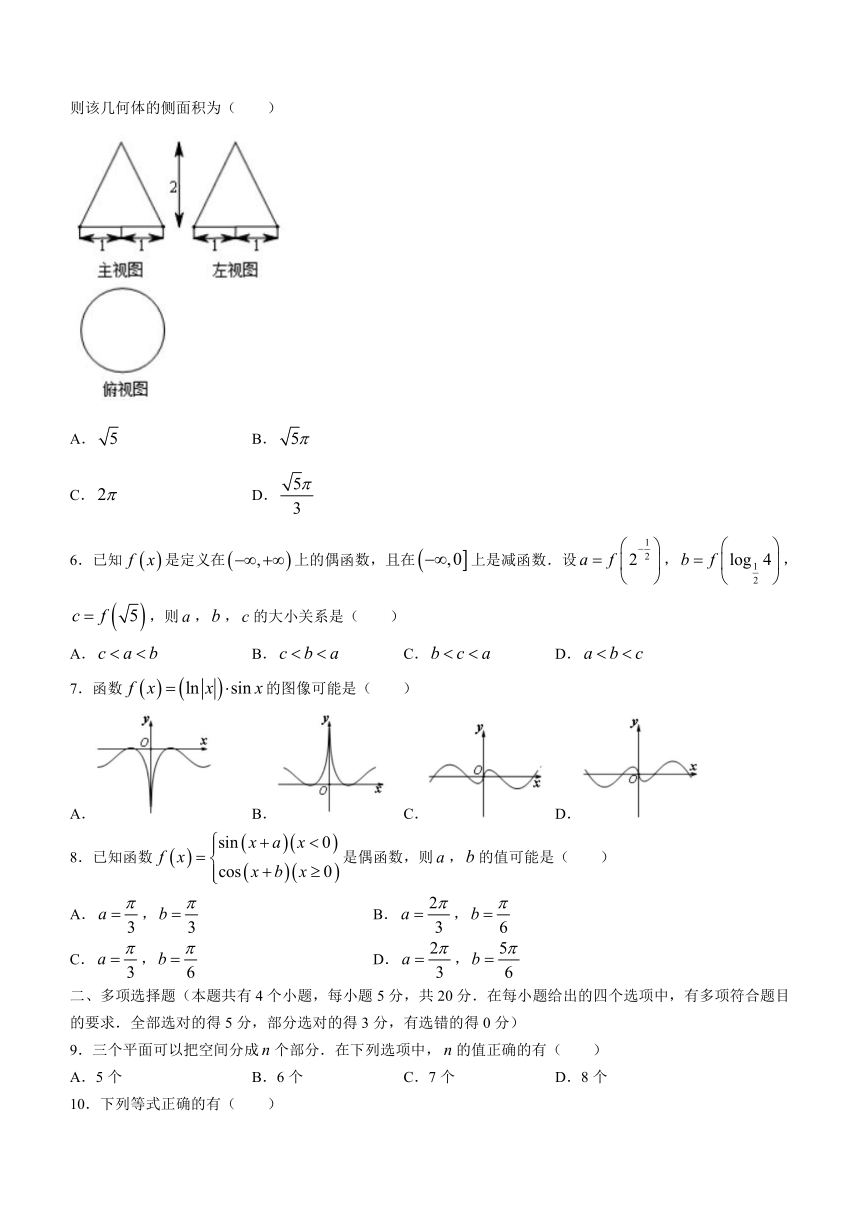


文档简介
绝密★考试结束前
2020学年第二学期衢温“5+1”联盟期中联考
高一年级数学学科 试题
考生须知:
1.本卷共4页满分150分,考试时间120分钟;
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字;
3.所有答案必须写在答题纸上,写在试卷上无效;
4.考试结束后,只需上交答题纸.
选择题部分(共60分)
一、单项选择题(本题共有8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个符合题目的要求)
1.已知全集false,集合false,false,则false=( )
A.false B.false C.false D.false
2.cos120°的值为( )
A.false B.false C.false D.false
3.如图,在正方体false中,false,false分别是正方形false与false的中心,直线false与false的位置关系为( )
A.平面 B.相交
C.异面 D.相交或异面
4.欧拉公式false(false为虚数单位)是由瑞士著名数学家欧拉提出的,它将指数函数的定义域扩大到复数集,则复数false在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.如图是某几何体的三视图,主视图和左视图是底边长和高均为2的等腰三角形,俯视图是半径为1的圆,则该几何体的侧面积为( )
A.false B.false
C.false D.false
6.已知false是定义在false上的偶函数,且在false上是减函数.设false,false,false,则false,false,false的大小关系是( )
A.false B.false C.false D.false
7.函数false的图像可能是( )
A. B. C. D.
8.已知函数false是偶函数,则false,false的值可能是( )
A.false,false B.false,false
C.false,false D.false,false
二、多项选择题(本题共有4个小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目的要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.三个平面可以把空间分成false个部分.在下列选项中,false的值正确的有( )
A.5个 B.6个 C.7个 D.8个
10.下列等式正确的有( )
A.false B.false
C.false D.false
11.函数false在区间false上的值域为false,则false的值可能是( )
A.1 B.2 C.3 D.4
12.已知false,函数false满足:存在false,对任意的false,恒有false.则false可以是( )
A.false B.false C.false D.false
非选择题部分(共90分)
三、填空题(本题共4个小题,每小题5分,共20分)
13.已知false,false为单位向量,且false.则false与false的夹角为______.
14.已知false,false为两个正实数,且false恒成立.则实数false的取值范围是______.
15.在false中,三个内角false,false,false所对的边分别为false,false,false,其中false,false,false.则false=______.
16.若平面向量false,false,false满足false,false,false.则false的最大值为______.
四、解答题(本题共6个小题,共70分.解答应写出文字说明,证明过程或验算步骤)
17.(本小题满分10分)已知集合false,false.
(1)当false时,求false;
(2)若false为非空集合且“false”是“false”的充分不必要条件,求实数false的取值范围.
18.(本小题满分12分)已知false,false,false.
(1)求函数false的最小正周期和单调递增区间;
(2)已知false三个内角false,false,false所对的边分别为false,false,false,当false,false,false时,求false的面积.
19.(本小题满分12分)最近,考古学家再次对四川广汉“三星堆古墓”进行考古发掘.科学家通过古生物中某种放射性元素的存量来估算古生物的年代.已知某放射性元素的半衰期约为4200年(即:每经过4200年,该元素的存量为原来的一半),已知古生物中该元素的初始存量为false.(参考数据:false)
(1)写出该元素的存量false与时间false(年)的关系;
(2)经检测古生物中该元素现在的存量为false,请推算古生物距今大约多少年?
20.(本小题满分12分)已知函数false是偶函数.
(1)求false的值;
(2)若false对于任意false恒成立,求实数false的取值范围.
21.(本小题满分12分)如图一,在平面几何中,有如下命题“正三角形false的高为false,false是false内任意一点,则false到三边的距离的和为定值false.当false是false的中心时,false到各边的距离均为false”.
证明如下:设正三角形false边长为false,高false,false到三边的距离分别为false,false,false
则:false,即:
false 化简得false
若false是false中心,则false
即:正三角形中心到各边的距离均为false
类比此命题及证明方法,在立体几何中,请写出高为false的正四面体false(图二)相应的命题,并证明你的结论.
22.(本小题满分12分)已知函数false.
(1)若false,求函数false的定义域;
(2)若false,且false有两个不同的实数根,求实数a的取值范围;
(3)是否存在实数false,使得函数false的定义域为false,且在false上具有单调性,若存在,求出false的取值范围;若不存在,说明理由.
2020学年第二学期衢温“5+1”联盟期中联考
高一年级数学学科 参考答案
一、单项选择题(本题共有8个小题,每小题5分,共40分.
1.B 2.A 3.C 4.A
5.B 6.D 7.D 8.C
二、多项选择题(本题共有4个小题,每小题5分,共20分.
9.BCD 10.ABD 11.BCD 12.AB
三、填空题(本小题共4个小题,每小题5分,共20分)
13.false 14.false 15.1或2 16.false
四、解答题(本题共6个小题,共70分.解答应写出文字说明,证明过程或验算步骤)
17.解:(1)依题意知:false
由false,得:false
即:false
false
(2)依题意得:false
false,解得false
因此,false的取值范围是false
18.解:(1)false
false
∴false,
当false时,
解得:false
即:单调递增区间为false
(2)由题意得:false,∴false∴false
由余弦定理知:false
∴false
∴false
19.解:(1)false
(2)∵false
∴false
解得:false
即:古生物距今大约5600年
20.解:由题意得:false
即false
∴false,∴false
(2)由题意得:false恒成立
∴false ∴false
∴false恒成立
∴false
∴false
21.解:类比命题:正四面体false的高为false,false是正四面体false内任意一点,则false到四个面的距离之和为定值false.当false是正四面体false的中心时,false到各面的距离均为false
证明如下:设四个面的面积为false
连结false,false,false,false,设false到四个面的距离分别是false,false,false,false,
则:false
∴false
化简得:false
若false是正四面体false的中心,则false
即:正四面体中心到各面的距离均为false.
22.解:(1)当false时,false,
由false,得false,解得false或false.
∴函数的定义域为false;
(2)false,false
设false,∴false有两个不同实数根,整理得false,false
同时false,∴false
(3)函数false的定义域为false,false恒成立,false
当false时,false,在false上单调递减,
此时需要满足false,即false,函数false在false上递减;
当false时,false,在false上递减,
∵false,∴false,即当false时,函数false在false上递减.
综上,当false时,函数false在定义域false上连续,且单调递减.
2020学年第二学期衢温“5+1”联盟期中联考
高一年级数学学科 试题
考生须知:
1.本卷共4页满分150分,考试时间120分钟;
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字;
3.所有答案必须写在答题纸上,写在试卷上无效;
4.考试结束后,只需上交答题纸.
选择题部分(共60分)
一、单项选择题(本题共有8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个符合题目的要求)
1.已知全集false,集合false,false,则false=( )
A.false B.false C.false D.false
2.cos120°的值为( )
A.false B.false C.false D.false
3.如图,在正方体false中,false,false分别是正方形false与false的中心,直线false与false的位置关系为( )
A.平面 B.相交
C.异面 D.相交或异面
4.欧拉公式false(false为虚数单位)是由瑞士著名数学家欧拉提出的,它将指数函数的定义域扩大到复数集,则复数false在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.如图是某几何体的三视图,主视图和左视图是底边长和高均为2的等腰三角形,俯视图是半径为1的圆,则该几何体的侧面积为( )
A.false B.false
C.false D.false
6.已知false是定义在false上的偶函数,且在false上是减函数.设false,false,false,则false,false,false的大小关系是( )
A.false B.false C.false D.false
7.函数false的图像可能是( )
A. B. C. D.
8.已知函数false是偶函数,则false,false的值可能是( )
A.false,false B.false,false
C.false,false D.false,false
二、多项选择题(本题共有4个小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目的要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.三个平面可以把空间分成false个部分.在下列选项中,false的值正确的有( )
A.5个 B.6个 C.7个 D.8个
10.下列等式正确的有( )
A.false B.false
C.false D.false
11.函数false在区间false上的值域为false,则false的值可能是( )
A.1 B.2 C.3 D.4
12.已知false,函数false满足:存在false,对任意的false,恒有false.则false可以是( )
A.false B.false C.false D.false
非选择题部分(共90分)
三、填空题(本题共4个小题,每小题5分,共20分)
13.已知false,false为单位向量,且false.则false与false的夹角为______.
14.已知false,false为两个正实数,且false恒成立.则实数false的取值范围是______.
15.在false中,三个内角false,false,false所对的边分别为false,false,false,其中false,false,false.则false=______.
16.若平面向量false,false,false满足false,false,false.则false的最大值为______.
四、解答题(本题共6个小题,共70分.解答应写出文字说明,证明过程或验算步骤)
17.(本小题满分10分)已知集合false,false.
(1)当false时,求false;
(2)若false为非空集合且“false”是“false”的充分不必要条件,求实数false的取值范围.
18.(本小题满分12分)已知false,false,false.
(1)求函数false的最小正周期和单调递增区间;
(2)已知false三个内角false,false,false所对的边分别为false,false,false,当false,false,false时,求false的面积.
19.(本小题满分12分)最近,考古学家再次对四川广汉“三星堆古墓”进行考古发掘.科学家通过古生物中某种放射性元素的存量来估算古生物的年代.已知某放射性元素的半衰期约为4200年(即:每经过4200年,该元素的存量为原来的一半),已知古生物中该元素的初始存量为false.(参考数据:false)
(1)写出该元素的存量false与时间false(年)的关系;
(2)经检测古生物中该元素现在的存量为false,请推算古生物距今大约多少年?
20.(本小题满分12分)已知函数false是偶函数.
(1)求false的值;
(2)若false对于任意false恒成立,求实数false的取值范围.
21.(本小题满分12分)如图一,在平面几何中,有如下命题“正三角形false的高为false,false是false内任意一点,则false到三边的距离的和为定值false.当false是false的中心时,false到各边的距离均为false”.
证明如下:设正三角形false边长为false,高false,false到三边的距离分别为false,false,false
则:false,即:
false 化简得false
若false是false中心,则false
即:正三角形中心到各边的距离均为false
类比此命题及证明方法,在立体几何中,请写出高为false的正四面体false(图二)相应的命题,并证明你的结论.
22.(本小题满分12分)已知函数false.
(1)若false,求函数false的定义域;
(2)若false,且false有两个不同的实数根,求实数a的取值范围;
(3)是否存在实数false,使得函数false的定义域为false,且在false上具有单调性,若存在,求出false的取值范围;若不存在,说明理由.
2020学年第二学期衢温“5+1”联盟期中联考
高一年级数学学科 参考答案
一、单项选择题(本题共有8个小题,每小题5分,共40分.
1.B 2.A 3.C 4.A
5.B 6.D 7.D 8.C
二、多项选择题(本题共有4个小题,每小题5分,共20分.
9.BCD 10.ABD 11.BCD 12.AB
三、填空题(本小题共4个小题,每小题5分,共20分)
13.false 14.false 15.1或2 16.false
四、解答题(本题共6个小题,共70分.解答应写出文字说明,证明过程或验算步骤)
17.解:(1)依题意知:false
由false,得:false
即:false
false
(2)依题意得:false
false,解得false
因此,false的取值范围是false
18.解:(1)false
false
∴false,
当false时,
解得:false
即:单调递增区间为false
(2)由题意得:false,∴false∴false
由余弦定理知:false
∴false
∴false
19.解:(1)false
(2)∵false
∴false
解得:false
即:古生物距今大约5600年
20.解:由题意得:false
即false
∴false,∴false
(2)由题意得:false恒成立
∴false ∴false
∴false恒成立
∴false
∴false
21.解:类比命题:正四面体false的高为false,false是正四面体false内任意一点,则false到四个面的距离之和为定值false.当false是正四面体false的中心时,false到各面的距离均为false
证明如下:设四个面的面积为false
连结false,false,false,false,设false到四个面的距离分别是false,false,false,false,
则:false
∴false
化简得:false
若false是正四面体false的中心,则false
即:正四面体中心到各面的距离均为false.
22.解:(1)当false时,false,
由false,得false,解得false或false.
∴函数的定义域为false;
(2)false,false
设false,∴false有两个不同实数根,整理得false,false
同时false,∴false
(3)函数false的定义域为false,false恒成立,false
当false时,false,在false上单调递减,
此时需要满足false,即false,函数false在false上递减;
当false时,false,在false上递减,
∵false,∴false,即当false时,函数false在false上递减.
综上,当false时,函数false在定义域false上连续,且单调递减.
同课章节目录
