必修2《曲线运动》复习
图片预览


文档简介
5-1
一、曲线运动
1.曲线运动的速度方向
做曲线运动的物体,在某点的速度方向,就是通过这一点的轨迹的________方向.物体在曲线运动中的速度方向时刻在改变,所以曲线运动一定是________速运动.
2.物体做曲线运动的条件:物体所受的________的方向与________方向不在同一直线上,也就是加速度方向与速度方向不在同一直线上.
当物体受到的合外力的方向与速度方向的夹角为锐角时,物体做曲线运动的速率将________;当物体受到的合外力的方向与速度方向的夹角为钝角时,物体做曲线运动的速率将________;当物体受到的合外力的方向与速度的方向垂直时,该力只改变速度方向,不改变速度的大小.
3.曲线运动的分类
4.曲线运动的轨迹
做曲线运动的物体,其轨迹向合外力所指一方弯曲,若已知物体的运动轨迹,可判断出物体所受合力的大致方向.如平抛运动的轨迹向下弯曲,圆周运动的轨迹总向圆心弯曲等.
二、合运动与分运动的关系
1.等时性:合运动和各分运动经历的________相等.即同时开始,同时进行,同时停止.
2.独立性:一个物体同时参与几个分运动,各分运动________进行,不受其他分运动的影响.物体的实际运动是这几个分运动的合运动.
3.等效性:各分运动的规律叠加起来与合运动的规律有完全相同的________.
三、运动的合成与分解的方法
1.运动的合成与分解:包括位移、速度、加速度的合成和分解.它们和力的合成与分解一样都遵守________定则,由已知的分运动求跟它们等效的合运动叫做运动的________,由已知的合运动求跟它等效的分运动叫做运动的________.
研究运动的合成和分解,目的在于把一些复杂的运动简化为比较简单的直线运动,这样就可以应用已经掌握的有关直线运动的规律,来研究一些复杂的曲线运动.
2.运动分解的基本方法
根据运动的________效果将描述合运动规律的各物理量(位移、速度、加速度)按平行四边形定则分别分解,或进行正交分解.
5-2/5-3
一、平抛运动的定义
将物体用一定的初速度沿________方向抛出,不考虑空气阻力,物体只在________作用下所做的运动叫做平抛运动.
二、平抛运动的性质
平抛运动是加速度为重力加速度(g)的________曲线运动,轨迹是抛物线.
三、平抛运动的研究方法
平抛运动可以分解为水平方向的________运动和竖直方向的________运动两个分运动.
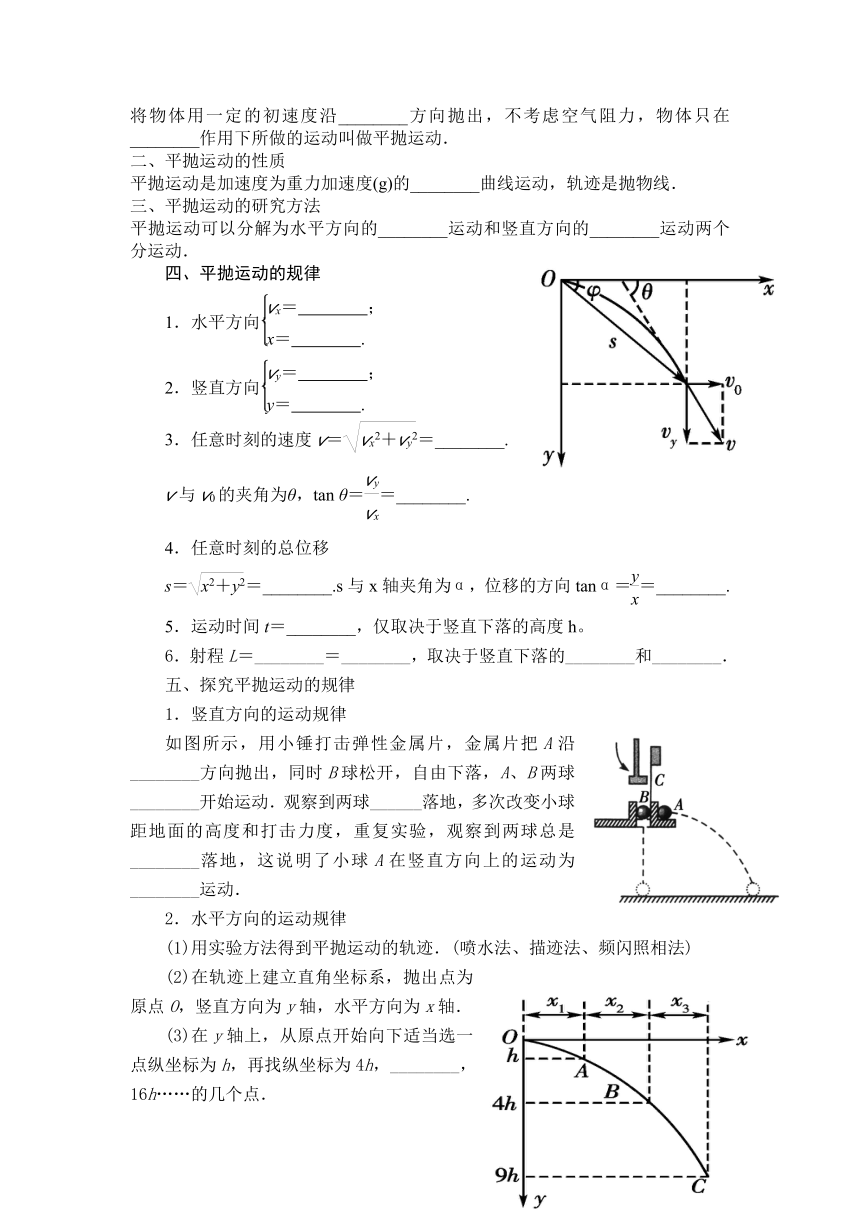
四、平抛运动的规律
1.水平方向
2.竖直方向
3.任意时刻的速度v==________.
v与v0的夹角为θ,tan θ==________.
4.任意时刻的总位移
s==________.s与x轴夹角为α,位移的方向tanα==________.
5.运动时间t=________,仅取决于竖直下落的高度h。
6.射程L=________=________,取决于竖直下落的________和________.
五、探究平抛运动的规律
1.竖直方向的运动规律
如图所示,用小锤打击弹性金属片,金属片把A沿________方向抛出,同时B球松开,自由下落,A、B两球________开始运动.观察到两球______落地,多次改变小球距地面的高度和打击力度,重复实验,观察到两球总是________落地,这说明了小球A在竖直方向上的运动为________运动.
2.水平方向的运动规律
(1)用实验方法得到平抛运动的轨迹.(喷水法、描迹法、频闪照相法)
(2)在轨迹上建立直角坐标系,抛出点为原点O,竖直方向为y轴,水平方向为x轴.
(3)在y轴上,从原点开始向下适当选一点纵坐标为h,再找纵坐标为4h,________,16h……的几个点.
(4)由对应点向轨迹作水平线,交点A、B、C……就是每经过相等时间物体到达的位置,如下图所示.
测量x轴上两相邻的水平位移,如近似相等,x1=x2=x3=……则水平方向为________运动.
六、总结与拓展:
1.飞行时间和水平射程
(1)飞行时间:t=,取决于物体下落的高度h,与初速度v0无关.
(2)水平射程:x=v0t=v0,由平抛初速度v0和下落高度h共同决定.
2.速度的变化规律
(1)任意时刻的速度水平分量均等于初速度V0.
(2)任意相等时间间隔Δt内的速度变化量均竖直向下,且ΔV=ΔVy=gΔt.
(3)任意两时刻的速度与速度变化量ΔV构成三角形,ΔV沿竖直方向.如图所示.
3.位移变化规律
(1)任意相等时间间隔内,水平位移不变,即Δx=v0Δt.
(2)连续相等的时间间隔Δt内,竖直方向上的位移差不变,即Δy=gΔt2.
(3)连续相等时间内的竖直位移之比为:
1∶3∶5∶…∶(2n-1)(n=1,2,3,…)
4.推论:
推论1:做平抛(或类平抛)运动的物体在任一时刻任一位置处,设其末速度方向与水平方向的夹角为θ,位移与水平方向的夹角为φ,则tan θ=2 tan φ.
证明:如图所示,由平抛运动规律得
tan θ==,
tan φ===,
所以tan θ=2tan φ.
推论2:做平抛(或类平抛)运动的物体任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点.如图中点为B点.
证明:设平抛物体的初速度为v0,从原点O到A点的时间为t,A点坐标为(x,y),B点坐标为(x′,0).
则x=v0t,
y=gt2,vy=gt,
又tan θ==,解得x′=.
5. 类平抛运动:
(1)类平抛运动的特点是物体所受的合力为恒力,且与初速度方向垂直(初速度v0方向不一定是水平方向,即合力的方向也不一定是竖直方向,且加速度大小不一定等于重力加速度g).
(2)平抛运动是典型的匀变速曲线运动,类平抛运动的特点与平抛运动相类似,所以处理平抛运动的思路和方法可以迁移到讨论类平抛运动中.
(3)类平抛运动可看成是沿初速度方向的匀速直线运动和垂直初速度方向(沿受力方向)的匀加速直线运动的合运动.但要分析清楚加速度的大小和方向.
5-4——5-7:
一、描述圆周运动的物理量
定义、意义 公式、单位
线速度 1.描述圆周运动的物体运动________的物理量(v).2.是矢量,方向和半径垂直,和圆周相切 1.v==________2.单位:m/s
角速度 1.描述物体绕圆心________的物理量(ω) 2.中学阶段不研究其方向 1.ω==________.2.单位:rad/s
周期和转速 1.周期是物体沿圆周运动________的时间:(T) 2.转速是物体单位时间内转过的________(n),也叫频率(f) 1.T=单位:s2.n的单位:r/s、r/min,f的单位:赫兹(Hz)
向心加速度 1.描述速度________变化快慢的物理量(a).2.方向指向________ 1.a==________.2.单位:m/s2
定义、意义 公式、单位
向心力 1.作用效果是产生向心加速度,只改变线速度的________,不改变线速度的________.2.方向指向________ 1.Fn=________=m.2.单位:N
相互关系 1.v=rω=r=2πrf2.a==rω2=ωv==4π2f2r3.Fn=m=mrω2=m=mωv=4π2mf2r
二、匀速圆周运动
1.特点:线速度的大小________,角速度、周期和频率都是恒定不变的,向心加速度和向心力的________也都是恒定不变的.
2.性质:是速度大小________,而速度方向时刻在变的变速曲线运动,并且加速度大小________,方向________变化的变加速曲线运动.
3.加速度和向心力:由于匀速圆周运动仅是速度方向________而速度大小________,故仅存在向心加速度.因此向心力就是做匀速圆周运动的物体所受外力的________.
4.质点做匀速圆周运动的条件:合外力大小________,方向始终与速度方向________且指向________.
5.两个结论
(1)同一转动圆盘(或物体)上的各点________相同.
(2)皮带连接的两轮不打滑时,轮缘上各点的________大小相等.
三、离心运动和近心运动
1.离心现象条件分析
(1)做圆周运动的物体,由于________作用,使它不能沿切线方向飞出,当Fn=F外时,被限制着沿圆周运动,如图所示.
(2)当产生向心力的合外力消失时,F=0,物体便沿所在位置的________飞出去,如图中A直线所示.
(3)当提供向心力的合外力不完全消失,而只是小于需要的向心力,F′< mrω2,物体沿切线与圆周之间的一条________运动.如图中B曲线所示.
2.近心运动
当提供向心力的合外力________做圆周运动所需要的向心力时,F′>mrω2,物体离圆心将越来越近,即为近心运动,如图中C曲线所示.
3.离心运动的应用和危害
利用离心运动制成离心机械.如:离心干燥器、洗衣机的脱水筒等.
汽车、火车转弯处,为防止离心运动造成的危害,一是限定汽车和火车的转弯速度不能太大;二是把路面(或路基)筑成 的斜坡以增大向心力.
思考:是否所有做圆周运动的物体所受的合力一定指向圆心?
1.向心力是根据力的效果命名的,在分析做圆周运动物体的受力情况时,切不可在物体的相互作用力外再添加一个向心力.
2.向心力的来源
(1)做匀速圆周运动时,物体的合外力充当向心力.
(2)变速圆周运动中物体合外力沿垂直线速度方向的分量充当向心力.
说明:1.无论匀速圆周运动还是非匀速圆周运动,沿半径指向圆心的合力均为向心力.
2.当采用正交分解法分析向心力的来源时,做圆周运动的物体在坐标原点,一定有一个坐标轴沿半径指向圆心.
1.火车转弯问题
由于火车的质量很大,火车拐弯时所需的向心力就很大.如果铁轨内外侧一样高,则外侧轮缘所受的压力很大,容易损坏.所以,实际中使转弯处的外侧轨道略高于内侧轨道,从而使支持力和重力的合力提供火车转弯时所需的向心力.
若铁轨转弯处半径为R,内外轨高度差为H,两轨间距为L,火车总质量为M,则
(1)火车在拐弯处运动的“规定速度”,即内外轨均不受侧面挤压的速度vp=;
(2)若火车实际速度大于vp,则外轨将受到侧向压力;
(3)若火车实际速度小于vp,则内轨将受到侧向压力.
2.“水流星”问题
用绳系装满水的杯子在竖直平面内做圆周运动,即使到了最高点杯子中的水也不会流出,这是因为水的重力提供水做圆周运动的向心力.
(2)当杯子在最高点速度v1>vmin时,杯子内的水对杯底有压力;若计算中求得杯子在最高点速度v2在分析传动装置的各物理量时,要抓住不等量和相等量的关系,表现为:
1.同一转轴的各点角速度ω相同,而线速度v=ωr与半径r成正比,向心加速度大小a=rω2与半径r成正比.
2.当皮带不打滑时,传动皮带、用皮带连接的两轮边沿上的各点线速度大小相等,而角速度ω=vr与半径r成反比,向心加速度大小a=v2/r与半径r成反比.
说明:采用齿轮传动时,两轮边沿的线速度大小相等,齿数与半径成正比,角速度与齿数成反比.
物体在竖直平面内的圆周运动是典型的变速圆周运动,一般情况下只讨论最高点和最低点的情况.
1.绳约束物体做圆周运动
如图所示细绳系着的小球或在圆轨道内侧运动的小球,当它们通过最高点时,有FN+mg=mv2/r.因FN≥0,所以v≥,即为物体通过最高点的速度的临界值.
(1)v=时,FN=0,物体刚好通过轨道最高点,对绳无拉力或对轨道无压力.
(2)v>时,FN>0,物体能通过轨道最高点,对绳有拉力或对轨道有压力.
(3)v<时,物体没有达到轨道最高点便脱离了轨道.
2.在轻杆或管的约束下的圆周运动
如图所示杆和管对物体能产生拉力,也能产生支持力.当物体通过最高点时有FN+mg=mv2/r,因为FN可以为正(拉力),也可以为负(支持力),还可以为零,故物体通过最高点的速度可以为任意值.
(1)当v=0时,FN=-mg,负号为支持力.
(2)当v=时,FN=0,对物体无作用力.
(3)当0(4)当v>时,FN>0,对物体产生指向圆心的弹力.
3.若是如图所示的小球,当v=时,重力恰好提供向心力,小球将脱离轨道做平抛运动,因为轨道对小球无作用力.
一、曲线运动
1.曲线运动的速度方向
做曲线运动的物体,在某点的速度方向,就是通过这一点的轨迹的________方向.物体在曲线运动中的速度方向时刻在改变,所以曲线运动一定是________速运动.
2.物体做曲线运动的条件:物体所受的________的方向与________方向不在同一直线上,也就是加速度方向与速度方向不在同一直线上.
当物体受到的合外力的方向与速度方向的夹角为锐角时,物体做曲线运动的速率将________;当物体受到的合外力的方向与速度方向的夹角为钝角时,物体做曲线运动的速率将________;当物体受到的合外力的方向与速度的方向垂直时,该力只改变速度方向,不改变速度的大小.
3.曲线运动的分类
4.曲线运动的轨迹
做曲线运动的物体,其轨迹向合外力所指一方弯曲,若已知物体的运动轨迹,可判断出物体所受合力的大致方向.如平抛运动的轨迹向下弯曲,圆周运动的轨迹总向圆心弯曲等.
二、合运动与分运动的关系
1.等时性:合运动和各分运动经历的________相等.即同时开始,同时进行,同时停止.
2.独立性:一个物体同时参与几个分运动,各分运动________进行,不受其他分运动的影响.物体的实际运动是这几个分运动的合运动.
3.等效性:各分运动的规律叠加起来与合运动的规律有完全相同的________.
三、运动的合成与分解的方法
1.运动的合成与分解:包括位移、速度、加速度的合成和分解.它们和力的合成与分解一样都遵守________定则,由已知的分运动求跟它们等效的合运动叫做运动的________,由已知的合运动求跟它等效的分运动叫做运动的________.
研究运动的合成和分解,目的在于把一些复杂的运动简化为比较简单的直线运动,这样就可以应用已经掌握的有关直线运动的规律,来研究一些复杂的曲线运动.
2.运动分解的基本方法
根据运动的________效果将描述合运动规律的各物理量(位移、速度、加速度)按平行四边形定则分别分解,或进行正交分解.
5-2/5-3
一、平抛运动的定义
将物体用一定的初速度沿________方向抛出,不考虑空气阻力,物体只在________作用下所做的运动叫做平抛运动.
二、平抛运动的性质
平抛运动是加速度为重力加速度(g)的________曲线运动,轨迹是抛物线.
三、平抛运动的研究方法
平抛运动可以分解为水平方向的________运动和竖直方向的________运动两个分运动.
四、平抛运动的规律
1.水平方向
2.竖直方向
3.任意时刻的速度v==________.
v与v0的夹角为θ,tan θ==________.
4.任意时刻的总位移
s==________.s与x轴夹角为α,位移的方向tanα==________.
5.运动时间t=________,仅取决于竖直下落的高度h。
6.射程L=________=________,取决于竖直下落的________和________.
五、探究平抛运动的规律
1.竖直方向的运动规律
如图所示,用小锤打击弹性金属片,金属片把A沿________方向抛出,同时B球松开,自由下落,A、B两球________开始运动.观察到两球______落地,多次改变小球距地面的高度和打击力度,重复实验,观察到两球总是________落地,这说明了小球A在竖直方向上的运动为________运动.
2.水平方向的运动规律
(1)用实验方法得到平抛运动的轨迹.(喷水法、描迹法、频闪照相法)
(2)在轨迹上建立直角坐标系,抛出点为原点O,竖直方向为y轴,水平方向为x轴.
(3)在y轴上,从原点开始向下适当选一点纵坐标为h,再找纵坐标为4h,________,16h……的几个点.
(4)由对应点向轨迹作水平线,交点A、B、C……就是每经过相等时间物体到达的位置,如下图所示.
测量x轴上两相邻的水平位移,如近似相等,x1=x2=x3=……则水平方向为________运动.
六、总结与拓展:
1.飞行时间和水平射程
(1)飞行时间:t=,取决于物体下落的高度h,与初速度v0无关.
(2)水平射程:x=v0t=v0,由平抛初速度v0和下落高度h共同决定.
2.速度的变化规律
(1)任意时刻的速度水平分量均等于初速度V0.
(2)任意相等时间间隔Δt内的速度变化量均竖直向下,且ΔV=ΔVy=gΔt.
(3)任意两时刻的速度与速度变化量ΔV构成三角形,ΔV沿竖直方向.如图所示.
3.位移变化规律
(1)任意相等时间间隔内,水平位移不变,即Δx=v0Δt.
(2)连续相等的时间间隔Δt内,竖直方向上的位移差不变,即Δy=gΔt2.
(3)连续相等时间内的竖直位移之比为:
1∶3∶5∶…∶(2n-1)(n=1,2,3,…)
4.推论:
推论1:做平抛(或类平抛)运动的物体在任一时刻任一位置处,设其末速度方向与水平方向的夹角为θ,位移与水平方向的夹角为φ,则tan θ=2 tan φ.
证明:如图所示,由平抛运动规律得
tan θ==,
tan φ===,
所以tan θ=2tan φ.
推论2:做平抛(或类平抛)运动的物体任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点.如图中点为B点.
证明:设平抛物体的初速度为v0,从原点O到A点的时间为t,A点坐标为(x,y),B点坐标为(x′,0).
则x=v0t,
y=gt2,vy=gt,
又tan θ==,解得x′=.
5. 类平抛运动:
(1)类平抛运动的特点是物体所受的合力为恒力,且与初速度方向垂直(初速度v0方向不一定是水平方向,即合力的方向也不一定是竖直方向,且加速度大小不一定等于重力加速度g).
(2)平抛运动是典型的匀变速曲线运动,类平抛运动的特点与平抛运动相类似,所以处理平抛运动的思路和方法可以迁移到讨论类平抛运动中.
(3)类平抛运动可看成是沿初速度方向的匀速直线运动和垂直初速度方向(沿受力方向)的匀加速直线运动的合运动.但要分析清楚加速度的大小和方向.
5-4——5-7:
一、描述圆周运动的物理量
定义、意义 公式、单位
线速度 1.描述圆周运动的物体运动________的物理量(v).2.是矢量,方向和半径垂直,和圆周相切 1.v==________2.单位:m/s
角速度 1.描述物体绕圆心________的物理量(ω) 2.中学阶段不研究其方向 1.ω==________.2.单位:rad/s
周期和转速 1.周期是物体沿圆周运动________的时间:(T) 2.转速是物体单位时间内转过的________(n),也叫频率(f) 1.T=单位:s2.n的单位:r/s、r/min,f的单位:赫兹(Hz)
向心加速度 1.描述速度________变化快慢的物理量(a).2.方向指向________ 1.a==________.2.单位:m/s2
定义、意义 公式、单位
向心力 1.作用效果是产生向心加速度,只改变线速度的________,不改变线速度的________.2.方向指向________ 1.Fn=________=m.2.单位:N
相互关系 1.v=rω=r=2πrf2.a==rω2=ωv==4π2f2r3.Fn=m=mrω2=m=mωv=4π2mf2r
二、匀速圆周运动
1.特点:线速度的大小________,角速度、周期和频率都是恒定不变的,向心加速度和向心力的________也都是恒定不变的.
2.性质:是速度大小________,而速度方向时刻在变的变速曲线运动,并且加速度大小________,方向________变化的变加速曲线运动.
3.加速度和向心力:由于匀速圆周运动仅是速度方向________而速度大小________,故仅存在向心加速度.因此向心力就是做匀速圆周运动的物体所受外力的________.
4.质点做匀速圆周运动的条件:合外力大小________,方向始终与速度方向________且指向________.
5.两个结论
(1)同一转动圆盘(或物体)上的各点________相同.
(2)皮带连接的两轮不打滑时,轮缘上各点的________大小相等.
三、离心运动和近心运动
1.离心现象条件分析
(1)做圆周运动的物体,由于________作用,使它不能沿切线方向飞出,当Fn=F外时,被限制着沿圆周运动,如图所示.
(2)当产生向心力的合外力消失时,F=0,物体便沿所在位置的________飞出去,如图中A直线所示.
(3)当提供向心力的合外力不完全消失,而只是小于需要的向心力,F′< mrω2,物体沿切线与圆周之间的一条________运动.如图中B曲线所示.
2.近心运动
当提供向心力的合外力________做圆周运动所需要的向心力时,F′>mrω2,物体离圆心将越来越近,即为近心运动,如图中C曲线所示.
3.离心运动的应用和危害
利用离心运动制成离心机械.如:离心干燥器、洗衣机的脱水筒等.
汽车、火车转弯处,为防止离心运动造成的危害,一是限定汽车和火车的转弯速度不能太大;二是把路面(或路基)筑成 的斜坡以增大向心力.
思考:是否所有做圆周运动的物体所受的合力一定指向圆心?
1.向心力是根据力的效果命名的,在分析做圆周运动物体的受力情况时,切不可在物体的相互作用力外再添加一个向心力.
2.向心力的来源
(1)做匀速圆周运动时,物体的合外力充当向心力.
(2)变速圆周运动中物体合外力沿垂直线速度方向的分量充当向心力.
说明:1.无论匀速圆周运动还是非匀速圆周运动,沿半径指向圆心的合力均为向心力.
2.当采用正交分解法分析向心力的来源时,做圆周运动的物体在坐标原点,一定有一个坐标轴沿半径指向圆心.
1.火车转弯问题
由于火车的质量很大,火车拐弯时所需的向心力就很大.如果铁轨内外侧一样高,则外侧轮缘所受的压力很大,容易损坏.所以,实际中使转弯处的外侧轨道略高于内侧轨道,从而使支持力和重力的合力提供火车转弯时所需的向心力.
若铁轨转弯处半径为R,内外轨高度差为H,两轨间距为L,火车总质量为M,则
(1)火车在拐弯处运动的“规定速度”,即内外轨均不受侧面挤压的速度vp=;
(2)若火车实际速度大于vp,则外轨将受到侧向压力;
(3)若火车实际速度小于vp,则内轨将受到侧向压力.
2.“水流星”问题
用绳系装满水的杯子在竖直平面内做圆周运动,即使到了最高点杯子中的水也不会流出,这是因为水的重力提供水做圆周运动的向心力.
(2)当杯子在最高点速度v1>vmin时,杯子内的水对杯底有压力;若计算中求得杯子在最高点速度v2
1.同一转轴的各点角速度ω相同,而线速度v=ωr与半径r成正比,向心加速度大小a=rω2与半径r成正比.
2.当皮带不打滑时,传动皮带、用皮带连接的两轮边沿上的各点线速度大小相等,而角速度ω=vr与半径r成反比,向心加速度大小a=v2/r与半径r成反比.
说明:采用齿轮传动时,两轮边沿的线速度大小相等,齿数与半径成正比,角速度与齿数成反比.
物体在竖直平面内的圆周运动是典型的变速圆周运动,一般情况下只讨论最高点和最低点的情况.
1.绳约束物体做圆周运动
如图所示细绳系着的小球或在圆轨道内侧运动的小球,当它们通过最高点时,有FN+mg=mv2/r.因FN≥0,所以v≥,即为物体通过最高点的速度的临界值.
(1)v=时,FN=0,物体刚好通过轨道最高点,对绳无拉力或对轨道无压力.
(2)v>时,FN>0,物体能通过轨道最高点,对绳有拉力或对轨道有压力.
(3)v<时,物体没有达到轨道最高点便脱离了轨道.
2.在轻杆或管的约束下的圆周运动
如图所示杆和管对物体能产生拉力,也能产生支持力.当物体通过最高点时有FN+mg=mv2/r,因为FN可以为正(拉力),也可以为负(支持力),还可以为零,故物体通过最高点的速度可以为任意值.
(1)当v=0时,FN=-mg,负号为支持力.
(2)当v=时,FN=0,对物体无作用力.
(3)当0
3.若是如图所示的小球,当v=时,重力恰好提供向心力,小球将脱离轨道做平抛运动,因为轨道对小球无作用力.
