沪科版九年级数学上册第22章第1节第4课时 平行线分线段成比例(共20张)
文档属性
| 名称 | 沪科版九年级数学上册第22章第1节第4课时 平行线分线段成比例(共20张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 20:30:22 | ||
图片预览


文档简介
(共20张PPT)
沪科版九年级数学上册第22章第1节第4课时
平行线分线段成比例
学习目标
理解并掌握平行线分线段成比例的基本事实及其推论并能灵活应用
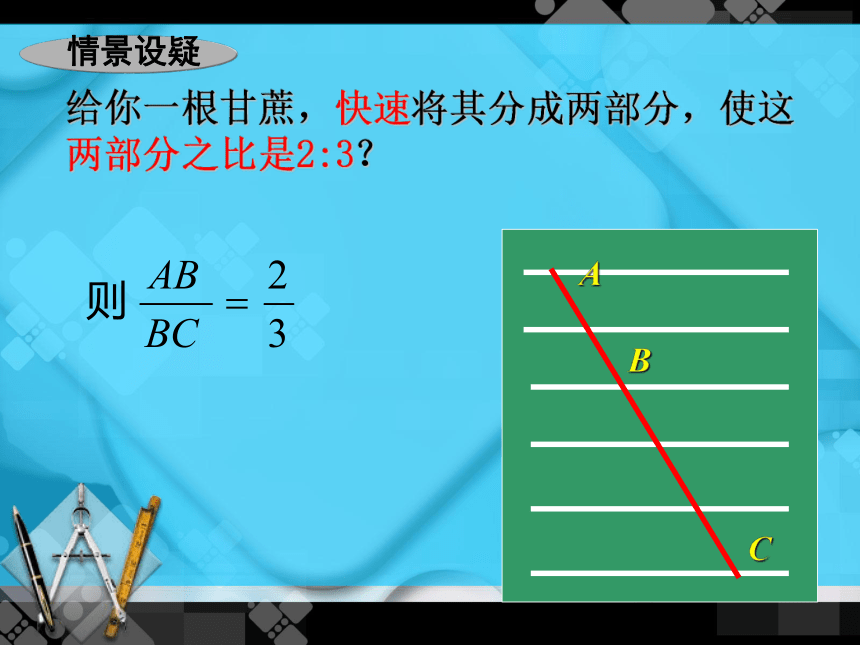
给你一根甘蔗,快速将其分成两部分,使这两部分之比是2:3?
A
B
C
情景设疑
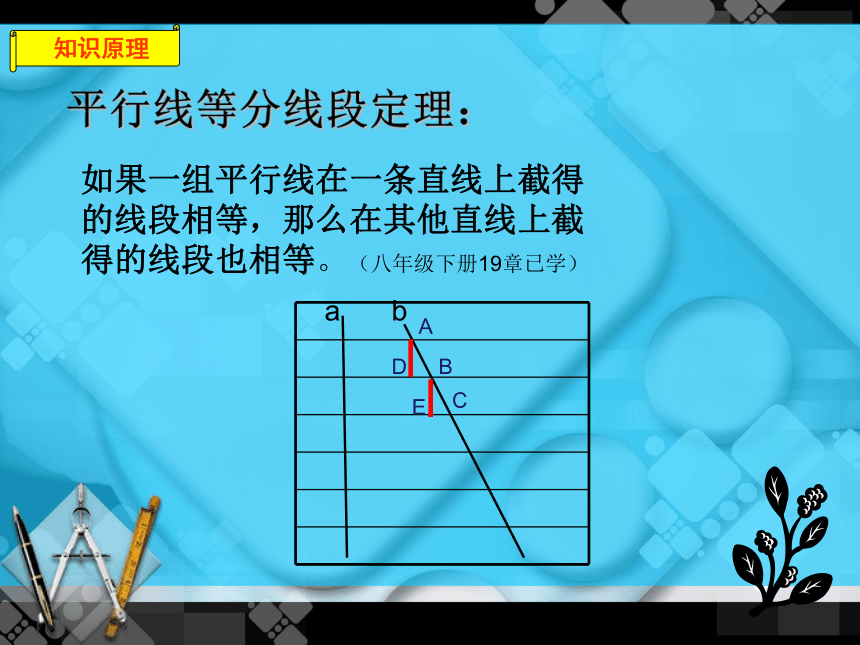
平行线等分线段定理:
如果一组平行线在一条直线上截得
的线段相等,那么在其他直线上截
得的线段也相等。(八年级下册19章已学)
b
知识原理
a
l
l
A
D
E
B
C
A
B
C
F
E
D
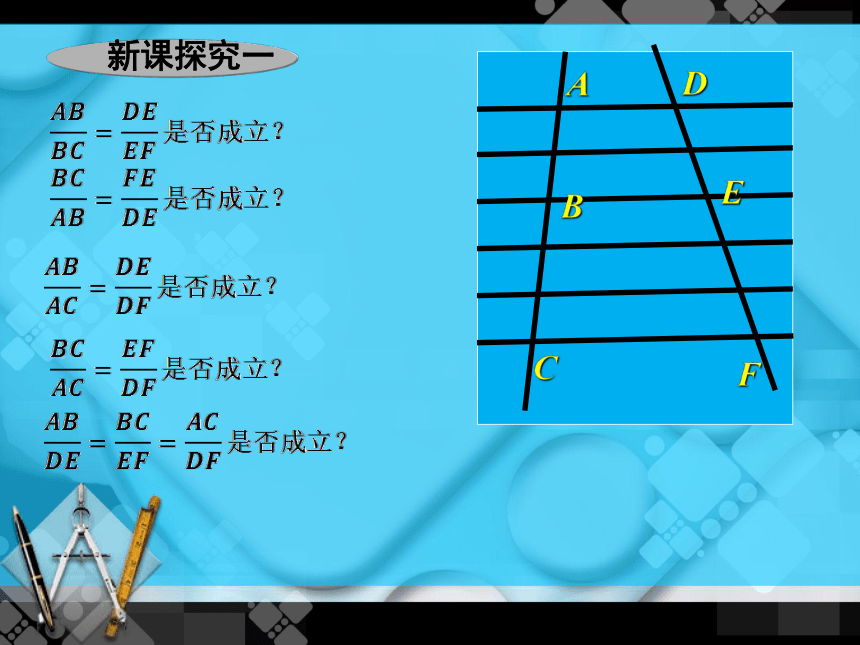
新课探究一
A
B
C
D
E
F
l1
l3
l2
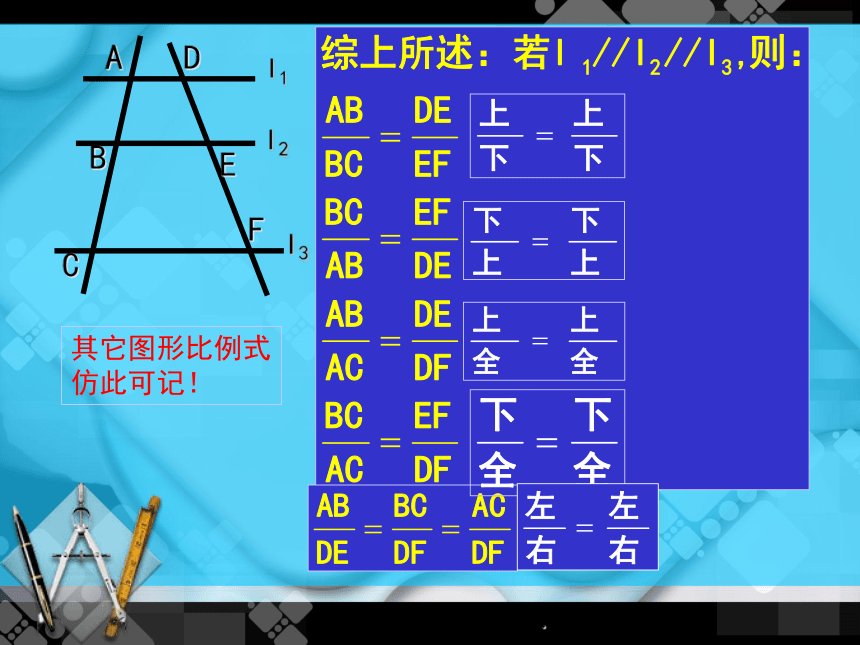
其它图形比例式
仿此可记!
.
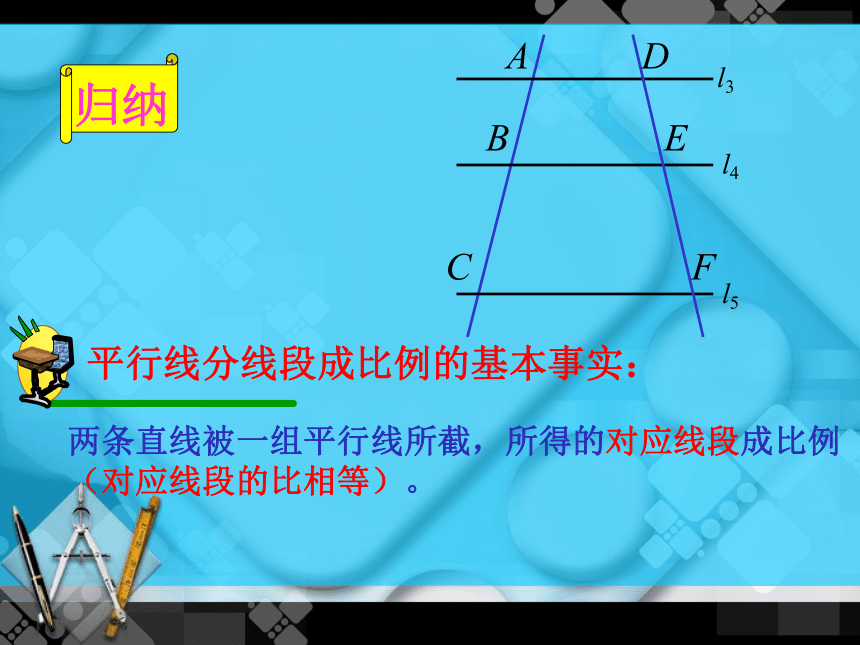
两条直线被一组平行线所截,所得的对应线段成比例
(对应线段的比相等)。
归纳
平行线分线段成比例的基本事实:
A
B
C
D
E
F
l3
l4
l5
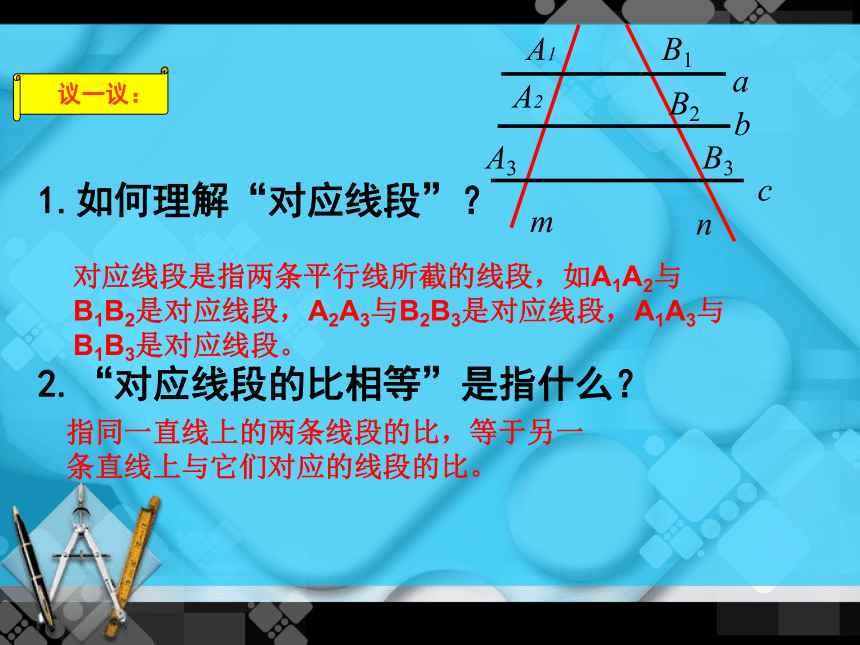
1.如何理解“对应线段”?
2.“对应线段的比相等”是指什么?
对应线段是指两条平行线所截的线段,如A1A2与B1B2是对应线段,A2A3与B2B3是对应线段,A1A3与B1B3是对应线段。
指同一直线上的两条线段的比,等于另一条直线上与它们对应的线段的比。
议一议:
A1
A2
A3
B1
B2
B3
b
c
m
n
a
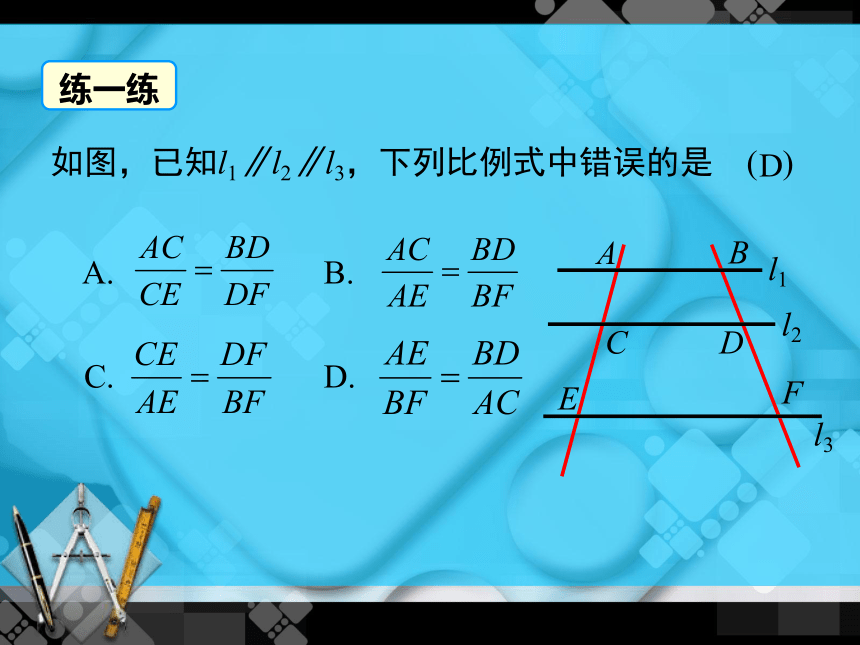
如图,已知l1∥l2∥l3,下列比例式中错误的是
(
)
A.
B.
C.
D.
D
练一练
A
C
E
B
D
F
l2
l1
l3
思考1
如果图1中l1
,
l2两条直线相交,交点刚好落到l3上,所得的对应线段的比会相等吗?依据是什么?
A
B
C
E
F
图2
l1
l2
(D)
图1
A
B
C
D
E
F
l3
l4
l5
新课探究二
思考2
如果图1中l1
,
l2两条直线相交,交点刚好落到l4上,所得的对应线段的比会相等吗?依据是什么?
D
A
B
E
F
C
l3
l4
l5
l1
l2
A(F)
B
C
E
D
图1
图2(2)
l2
l3
l1
l3
l
l?
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l?
“A”
“X”
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
平行线分线段成比例的推论:
如图,DE∥BC,
,则
;
FG∥BC,
,则
.
练一练
A
B
C
E
D
F
G
例1
如图,在△ABC中,
EF∥BC.
(1)
如果E、F分别是
AB
和
AC
上的点,
AE
=
BE=7,
FC
=
4
,那么
AF
的长是多少?
A
B
C
E
F
∴
∴
解得
AF
=
4.
典例精析
解:∵
EF∥BC
(2)
如果AB
=
10,AE=6,AF
=
5,那么
FC
的长是多
少?
A
B
C
E
F
∴
即
解得
AC
=
.
∴
FC
=
AC-AF
=
.
解:∵
EF∥BC
例2
如图D、E、F分别在OA、OB、OC上且DF∥AC,EF平行BC
求证:OD:OA=OE:OB
勇攀高峰
证明:
∵DF∥AC
∴
OD:OA=OF:OC
又∵EF∥BC
∴
OE:OB=OF:OC
∴
OD:OA=OE:OB
勇攀高峰
例3
如图在△ABC
中,D,G分别为AC,BC上的点,并且
DG∥AB.如果AC:BC=EF:FD,求证:AD=EB
D
B
C
A
E
F
G
1、平行线分线段成比例:
(1)两直线被一组平行线所截,所得的对应线段成比例(关键要能熟练地找出对应线段)
(2)平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
2、要熟悉该定理的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
课堂小结
3、注意该定理在三角形中的应用
注意:应用平行线分线段成比例定理得到的比例式中,四条线段与两直线的交点位置无关.
沪科版九年级数学上册第22章第1节第4课时
平行线分线段成比例
学习目标
理解并掌握平行线分线段成比例的基本事实及其推论并能灵活应用
给你一根甘蔗,快速将其分成两部分,使这两部分之比是2:3?
A
B
C
情景设疑
平行线等分线段定理:
如果一组平行线在一条直线上截得
的线段相等,那么在其他直线上截
得的线段也相等。(八年级下册19章已学)
b
知识原理
a
l
l
A
D
E
B
C
A
B
C
F
E
D
新课探究一
A
B
C
D
E
F
l1
l3
l2
其它图形比例式
仿此可记!
.
两条直线被一组平行线所截,所得的对应线段成比例
(对应线段的比相等)。
归纳
平行线分线段成比例的基本事实:
A
B
C
D
E
F
l3
l4
l5
1.如何理解“对应线段”?
2.“对应线段的比相等”是指什么?
对应线段是指两条平行线所截的线段,如A1A2与B1B2是对应线段,A2A3与B2B3是对应线段,A1A3与B1B3是对应线段。
指同一直线上的两条线段的比,等于另一条直线上与它们对应的线段的比。
议一议:
A1
A2
A3
B1
B2
B3
b
c
m
n
a
如图,已知l1∥l2∥l3,下列比例式中错误的是
(
)
A.
B.
C.
D.
D
练一练
A
C
E
B
D
F
l2
l1
l3
思考1
如果图1中l1
,
l2两条直线相交,交点刚好落到l3上,所得的对应线段的比会相等吗?依据是什么?
A
B
C
E
F
图2
l1
l2
(D)
图1
A
B
C
D
E
F
l3
l4
l5
新课探究二
思考2
如果图1中l1
,
l2两条直线相交,交点刚好落到l4上,所得的对应线段的比会相等吗?依据是什么?
D
A
B
E
F
C
l3
l4
l5
l1
l2
A(F)
B
C
E
D
图1
图2(2)
l2
l3
l1
l3
l
l?
A
B
C
D
E
l2
A
B
C
D
E
l1
l
l?
“A”
“X”
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
平行线分线段成比例的推论:
如图,DE∥BC,
,则
;
FG∥BC,
,则
.
练一练
A
B
C
E
D
F
G
例1
如图,在△ABC中,
EF∥BC.
(1)
如果E、F分别是
AB
和
AC
上的点,
AE
=
BE=7,
FC
=
4
,那么
AF
的长是多少?
A
B
C
E
F
∴
∴
解得
AF
=
4.
典例精析
解:∵
EF∥BC
(2)
如果AB
=
10,AE=6,AF
=
5,那么
FC
的长是多
少?
A
B
C
E
F
∴
即
解得
AC
=
.
∴
FC
=
AC-AF
=
.
解:∵
EF∥BC
例2
如图D、E、F分别在OA、OB、OC上且DF∥AC,EF平行BC
求证:OD:OA=OE:OB
勇攀高峰
证明:
∵DF∥AC
∴
OD:OA=OF:OC
又∵EF∥BC
∴
OE:OB=OF:OC
∴
OD:OA=OE:OB
勇攀高峰
例3
如图在△ABC
中,D,G分别为AC,BC上的点,并且
DG∥AB.如果AC:BC=EF:FD,求证:AD=EB
D
B
C
A
E
F
G
1、平行线分线段成比例:
(1)两直线被一组平行线所截,所得的对应线段成比例(关键要能熟练地找出对应线段)
(2)平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的对应线段成比例.
2、要熟悉该定理的几种基本图形
A
B
C
D
E
F
A
B
C
D
E
F
课堂小结
3、注意该定理在三角形中的应用
注意:应用平行线分线段成比例定理得到的比例式中,四条线段与两直线的交点位置无关.
