沪科版九年级数学上册 22.1 黄金分割课件(21张)
文档属性
| 名称 | 沪科版九年级数学上册 22.1 黄金分割课件(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 08:38:51 | ||
图片预览







文档简介
(共20张PPT)
黄金分割
(1)以下3张图片,哪张构图最美?
活动一:建立黄金分割的概念.
(2)芭蕾舞演员做相同的动作,踮脚尖和不踮脚尖,哪个更美?
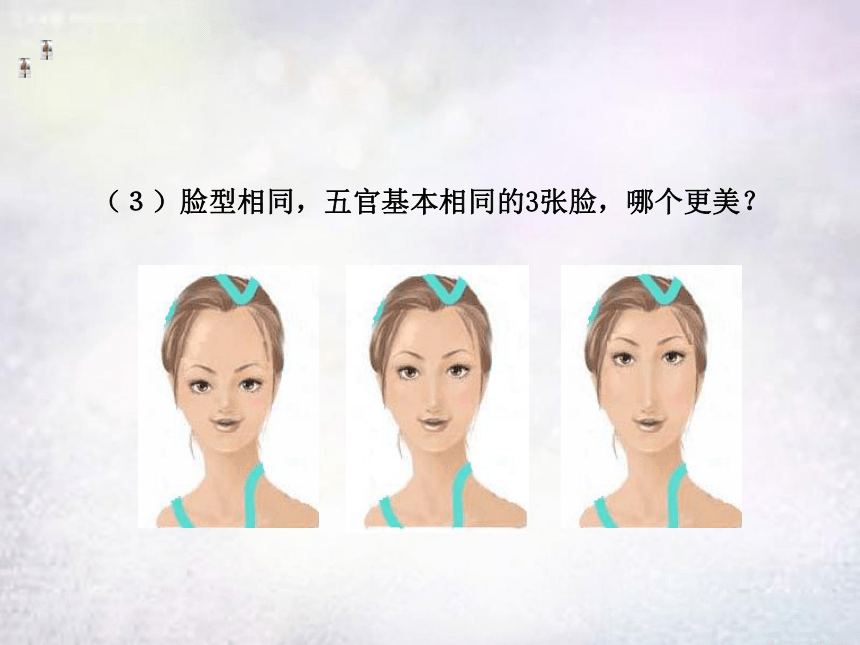
(3)脸型相同,五官基本相同的3张脸,哪个更美?
B
A
C
AC
AB
AC
BC
=
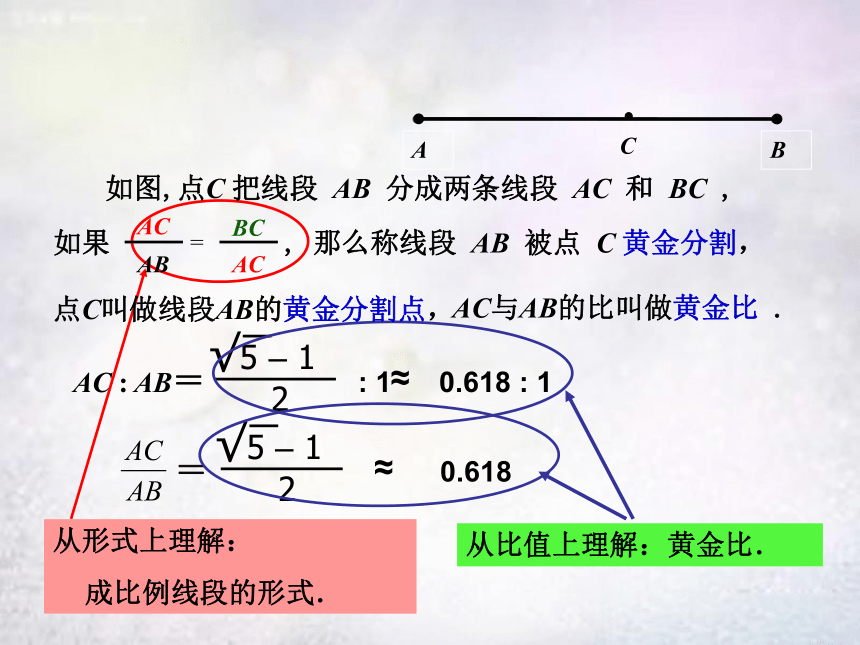
如果 , 那么称线段 AB 被点 C 黄金分割,
点C叫做线段AB的黄金分割点,
AC与AB的比叫做黄金比 .
如图,点C 把线段 AB 分成两条线段 AC 和 BC ,
A
B
利用一元二次方程知识可以解出x= ,
x2 + x–1=0
0.618
利用计算器计算 x = ≈ .(精确到千分位)
1–x
AC
AB
AC
BC
=
如果 , 那么称线段 AB 被点 C 黄金分割,
点C叫做线段AB的黄金分割点,
AC与AB的比叫做黄金比 .
如图,点C 把线段 AB 分成两条线段 AC 和 BC ,
C
A
B
活动二:探究黄金比.
设 AB=1,AC = x,则 BC= ,
由 列方程得: ,
化为整式方程: ,
1 – x
=
x
x
1
√5 – 1
2
≈
AC : AB= : 1 0.618 : 1
从形式上理解:
成比例线段的形式.
√5 – 1
2
≈
= 0.618
从比值上理解:黄金比.
AC
AB
AC
BC
=
如果 , 那么称线段 AB 被点 C 黄金分割,
点C叫做线段AB的黄金分割点,
AC与AB的比叫做黄金比 .
如图,点C 把线段 AB 分成两条线段 AC 和 BC ,
C
A
B
判断1:如图,线段AB上有一个点C,如果 ,
那么点C是线段AB的黄金分割点吗?
C
A
B
解:根据定义,如果 = ,那么点C叫作线段AB的
黄金分割点,
∵ , ∴ ,
∴ 点C是线段AB的黄金分割点.
=
活动三:运用黄金分割的概念进行判断.
判断2:如图,线段AB上有一个点C,如果AB=2,AC= ,
那么点C是线段AB的黄金分割点吗?
C
A
B
按照如下方法作图:
(1)经过点B作BD⊥AB,使BD= AB.
(2)连接AD,在AD上截取DE=DB.
(3)在AB上截取AC=AE.
1.已知线段AB,如何作出它的黄金分割点?
(1)如果设AB=2,那么BD= ,AD= ,AC= .
(2)计算 = .
2.根据上述作法回答下列问题:
3.点 C 是线段 AB 的黄金分割点吗
活动四:作图法确定线段的黄金分割点.
计算1:如图,点C是线段AB的黄金分割点,AC>BC,
如果AB=4,求线段AC的长度.
C
A
B
=
解:根据定义,如果点C是线段AB的黄金分割点,
那么 = ,
∵点C是线段AB的黄金分割点, ∴ ,
∴ AC= AB = .
×4 = 2( )
活动五:运用黄金分割的概念进行计算
计算2:
东方明珠塔,塔高463米.在设计的最初,设计师将塔身设计为直线型,后来,为了使平直单调的塔身变得丰富多彩,更协调、美观,设计师决定在靠近塔尖的黄金分割点处设计一个球体,请你计算这个球体距离地面的高度.(精确到百分位)
B
A
C
1.你身边有黄金分割的实例吗?
如何验证你的猜想呢?
活动六:寻找我们身边的黄金分割
分组测量,计算矩形1宽与长的比 .
1
2
3
宽与长的比是黄金比!
2.小实验:下列矩形中,哪个看起来更美?
你的身边有这样的矩形实例吗?
摄影构图通常运用的三分法就是黄金分割的演变,把长方形画面的长、宽各分成三等分,整个画面呈井字形分割,井字形分割的交叉点便是画面主体(视觉中心)的最佳位置,是最容易诱导人们视觉兴趣的视觉美点.
黄金分割的魅力
在人的面部,五官的分布越符合黄金分割,看起来就越美.
B
C
A
黄金分割的魅力
A
C
B
A
C
B
A
C
B
在礼品包装中,也经常用到黄金分割.
黄金分割的魅力
点滴收获
请你选择下面一个关键词,
谈谈你本节课的体会:
知识、思想、方法、收获、
喜悦、困惑、成功…...
E N D
黄金分割
(1)以下3张图片,哪张构图最美?
活动一:建立黄金分割的概念.
(2)芭蕾舞演员做相同的动作,踮脚尖和不踮脚尖,哪个更美?
(3)脸型相同,五官基本相同的3张脸,哪个更美?
B
A
C
AC
AB
AC
BC
=
如果 , 那么称线段 AB 被点 C 黄金分割,
点C叫做线段AB的黄金分割点,
AC与AB的比叫做黄金比 .
如图,点C 把线段 AB 分成两条线段 AC 和 BC ,
A
B
利用一元二次方程知识可以解出x= ,
x2 + x–1=0
0.618
利用计算器计算 x = ≈ .(精确到千分位)
1–x
AC
AB
AC
BC
=
如果 , 那么称线段 AB 被点 C 黄金分割,
点C叫做线段AB的黄金分割点,
AC与AB的比叫做黄金比 .
如图,点C 把线段 AB 分成两条线段 AC 和 BC ,
C
A
B
活动二:探究黄金比.
设 AB=1,AC = x,则 BC= ,
由 列方程得: ,
化为整式方程: ,
1 – x
=
x
x
1
√5 – 1
2
≈
AC : AB= : 1 0.618 : 1
从形式上理解:
成比例线段的形式.
√5 – 1
2
≈
= 0.618
从比值上理解:黄金比.
AC
AB
AC
BC
=
如果 , 那么称线段 AB 被点 C 黄金分割,
点C叫做线段AB的黄金分割点,
AC与AB的比叫做黄金比 .
如图,点C 把线段 AB 分成两条线段 AC 和 BC ,
C
A
B
判断1:如图,线段AB上有一个点C,如果 ,
那么点C是线段AB的黄金分割点吗?
C
A
B
解:根据定义,如果 = ,那么点C叫作线段AB的
黄金分割点,
∵ , ∴ ,
∴ 点C是线段AB的黄金分割点.
=
活动三:运用黄金分割的概念进行判断.
判断2:如图,线段AB上有一个点C,如果AB=2,AC= ,
那么点C是线段AB的黄金分割点吗?
C
A
B
按照如下方法作图:
(1)经过点B作BD⊥AB,使BD= AB.
(2)连接AD,在AD上截取DE=DB.
(3)在AB上截取AC=AE.
1.已知线段AB,如何作出它的黄金分割点?
(1)如果设AB=2,那么BD= ,AD= ,AC= .
(2)计算 = .
2.根据上述作法回答下列问题:
3.点 C 是线段 AB 的黄金分割点吗
活动四:作图法确定线段的黄金分割点.
计算1:如图,点C是线段AB的黄金分割点,AC>BC,
如果AB=4,求线段AC的长度.
C
A
B
=
解:根据定义,如果点C是线段AB的黄金分割点,
那么 = ,
∵点C是线段AB的黄金分割点, ∴ ,
∴ AC= AB = .
×4 = 2( )
活动五:运用黄金分割的概念进行计算
计算2:
东方明珠塔,塔高463米.在设计的最初,设计师将塔身设计为直线型,后来,为了使平直单调的塔身变得丰富多彩,更协调、美观,设计师决定在靠近塔尖的黄金分割点处设计一个球体,请你计算这个球体距离地面的高度.(精确到百分位)
B
A
C
1.你身边有黄金分割的实例吗?
如何验证你的猜想呢?
活动六:寻找我们身边的黄金分割
分组测量,计算矩形1宽与长的比 .
1
2
3
宽与长的比是黄金比!
2.小实验:下列矩形中,哪个看起来更美?
你的身边有这样的矩形实例吗?
摄影构图通常运用的三分法就是黄金分割的演变,把长方形画面的长、宽各分成三等分,整个画面呈井字形分割,井字形分割的交叉点便是画面主体(视觉中心)的最佳位置,是最容易诱导人们视觉兴趣的视觉美点.
黄金分割的魅力
在人的面部,五官的分布越符合黄金分割,看起来就越美.
B
C
A
黄金分割的魅力
A
C
B
A
C
B
A
C
B
在礼品包装中,也经常用到黄金分割.
黄金分割的魅力
点滴收获
请你选择下面一个关键词,
谈谈你本节课的体会:
知识、思想、方法、收获、
喜悦、困惑、成功…...
E N D
