沪科版 初中数学九年级上册 第22章 相似三角形的判定(共32张)
文档属性
| 名称 | 沪科版 初中数学九年级上册 第22章 相似三角形的判定(共32张) |  | |
| 格式 | zip | ||
| 文件大小 | 732.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 19:08:43 | ||
图片预览








文档简介
(共32张PPT)
22.2相似三角形的判定(第1课时)
本节课内容:
1.认识相似三角形,知道相似三角形的表示方
法及相似比.
2.学习一个定理:相似三角形判定的预备定理.
1.认识相似三角形:
回顾:什么样的两个多边形是相似多边形?
相似多边形:
边数相同
对应角相等
对应边长度的比相等
相似三角形:
对应角相等
对应边长度的比相等
相似三角形
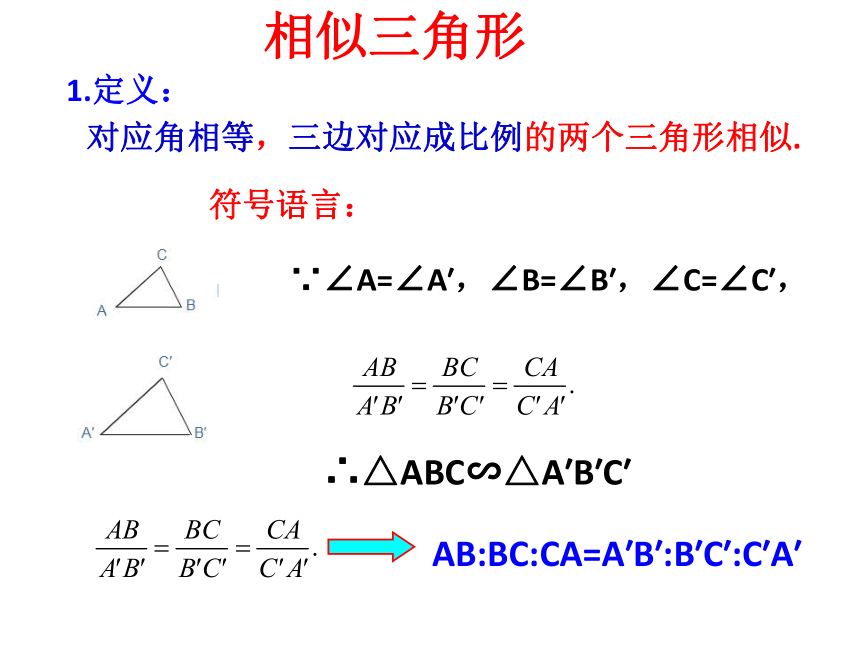
1.定义:
对应角相等,三边对应成比例的两个三角形相似.
符号语言:
∵∠A=∠A′,∠B=∠B′,∠C=∠C′,
∴△ABC∽△A′B′C′
AB:BC:CA=A′B′:B′C′:C′A′
2.
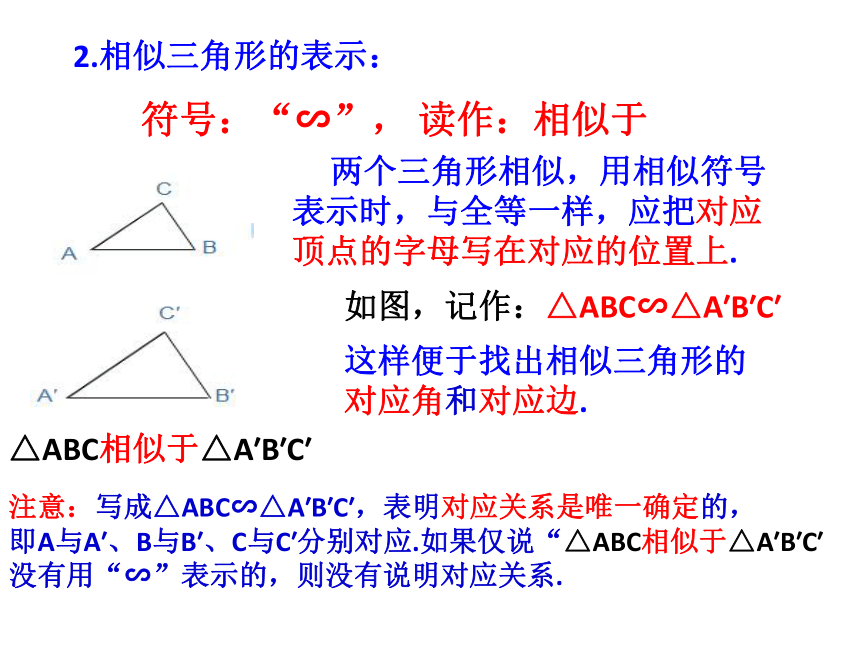
相似三角形的表示:
2.相似三角形的表示:
符号:“∽”,
读作:相似于
两个三角形相似,用相似符号表示时,与全等一样,应把对应顶点的字母写在对应的位置上.
△ABC相似于△A′B′C′
这样便于找出相似三角形的
对应角和对应边.
如图,记作:△ABC∽△A′B′C′
注意:写成△ABC∽△A′B′C′,表明对应关系是唯一确定的,
即A与A′、B与B′、C与C′分别对应.如果仅说“△ABC相似于△A′B′C′
没有用“∽”表示的,则没有说明对应关系.
3.
相似三角形的相似比:
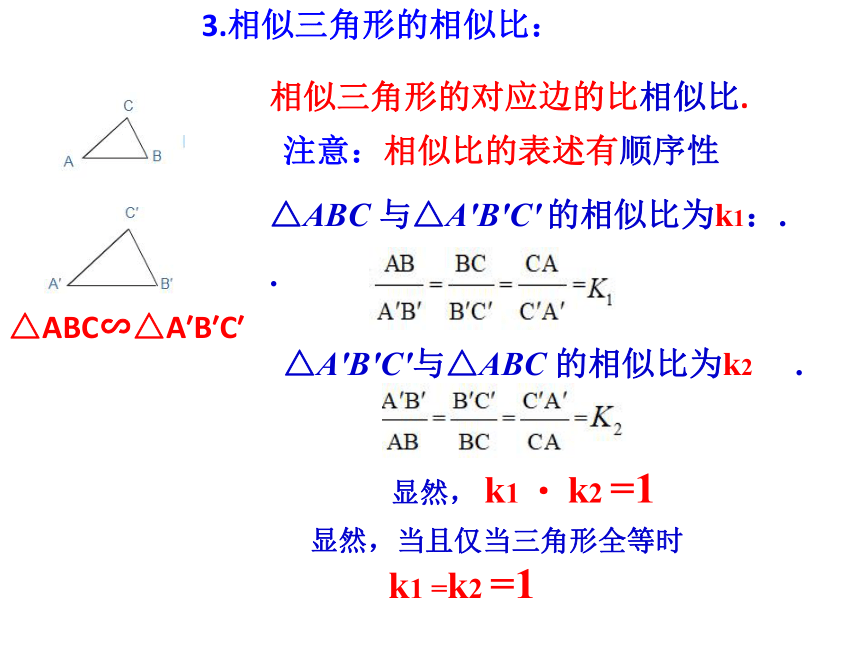
3.相似三角形的相似比:
△ABC∽△A′B′C′
相似三角形的对应边的比相似比.
注意:相似比的表述有顺序性
△ABC
与△A′B′C′
的相似比为k1:.
.
△A′B′C′与△ABC
的相似比为k2
.
显然,
k1
·
k2
=1
显然,当且仅当三角形全等时
k1
=k2
=1
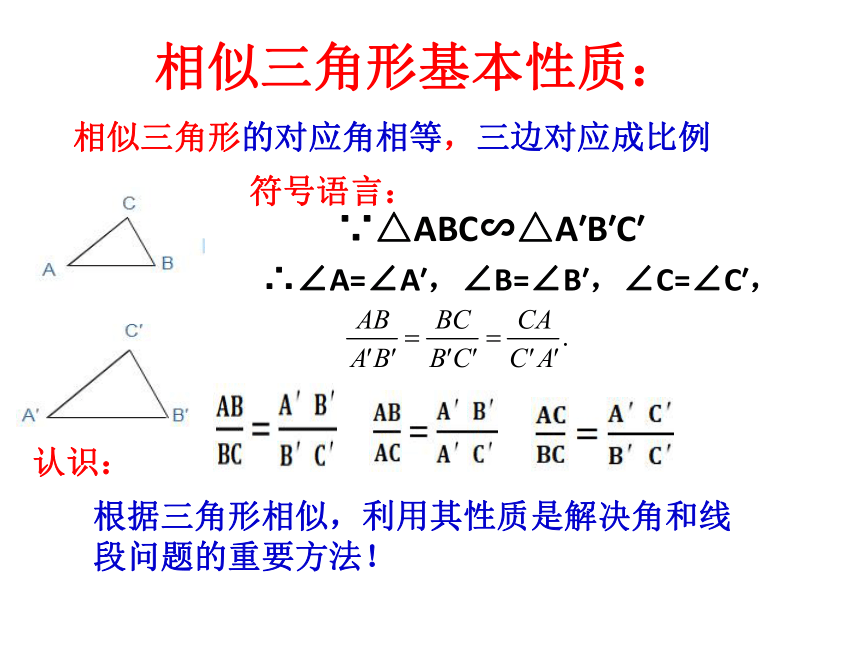
相似三角形基本性质:
相似三角形的对应角相等,三边对应成比例
符号语言:
∵△ABC∽△A′B′C′
∴∠A=∠A′,∠B=∠B′,∠C=∠C′,
认识:
根据三角形相似,利用其性质是解决角和线段问题的重要方法!
4.相似三角形判定的预备定理:
温故知新:
平行线分线段成比例定理的推论?
推论:平行于三角形一边的直线和其他两边
(或两边延长线)相交,截得的对应线段成比例
A
C
B
F
E
A
F
E
C
B
EF∥BC
大胆猜测:
△AEF与△ABC相似
平行于三角形一边的直线和其他两边(或两边的延长线)
相交,截的三角形与原三角形相似。
求证:
已知:DE//BC
求证:△ADE∽△ABC
1.根据相似三角形的定义△ADE与
△ABC相似必须满足哪些条件?
分析:
∠A=∠A,∠ADE=∠B,
∠
AED=∠C,
2.已经具备哪些条件?为什么?还需要什么条件?
已有条件:∠A=∠A,∠ADE=∠B,
∠AED=∠C
,
A
D
B
C
E
A
E
A
C
E
A
C
E
A
B
C
E
A
D
B
C
A
图2
还需条件:
分析:
3.关键:
A
D
E
B
C
启发:将DE平移到BC上
此时,DF∥AC
F
类比、转化思想!
实际作图,我们作DF∥AC
已知:DE//BC
求证:△ADE∽△ABC
证明:
F
作DF∥AC,交BC于点F
则DE=FC,
∵DE∥BC,
∴∠A=∠A,∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC
E
D
A
C
B
已知:DE//BC
求证:△ADE∽△ABC
F
证明:
作DF∥EC,交BC延长线于点F
∵DE∥BC,
∴△ADE∽△ABC
则DE=FC,
∴∠EAD=∠BAC,∠ADE=∠B,∠AED=∠ACB,
E
D
A
C
B
已知:DE//BC
求证:△ADE∽△ABC
F
证明:
在AB上截取AF=AE
G
作FG∥BC,交AC于点G
由前面结论,得△AFG∽△ABC
∵DE∥BC,
∴DE∥FG,
∴∠D=∠AFG,∠E=∠AGF,
∴△ADE≌△AFG
∴△ADE∽△ABC
E
D
A
C
B
∵DE∥BC,
∴△ADE∽△ABC
平行于三角形一边的直线和其他两边(或两边的延长线)
相交,截的三角形与三角形相似。
相似三角形判定的预备定理
符号语言:
“A”型
“X”型
E
D
A
C
B
∵DE∥BC,
∴△ADE∽△ABC
线段必须是边
例题巩固:
注意:
根据两个定理和推论,利用平行线得到线段成比例,是解决线段问题的重要方法!
教材P78.练习:
F
DE∥BC,
DF∥AC,
判断正误:
巩固练习
如图,在
ABCD中,DE交BC于F,交AB的延长线于点E.
(1)请写出图中相似的三角形;
(2)请由其中的一对相似三角形写出相应的比例式;
F
A
B
C
D
E
△CDF∽
△BEF
,
△BEF∽△AED
△CDF∽△AED
也可写成
△BEF∽△CDF∽△AED
(1)∵DE∥BC,
∴△ADE∽△ABC
(2)∵DE∥BC,
5EC=12
EC=2.4
2
3
4
6
4
∵CF=BF
如图,△ABC中BD是角平分线,过点D作DE∥AB交BC于E,AB=5cm,
BE=3cm,求EC的长.
A
B
C
D
E
1
2
5
3
x
解:∵DE∥AB,
∠2=∠3
3
∵∠1=∠2
∴∠1=∠3
∴DE=BE=3
3(x+3)=5x
x=4.5
∴△CDE∽△CAB
(1):证明:∵AB=2EB,
AB=2DC,
∴EB=DC,
又,BE∥DC,
∴四边形BCDE是平行四边形
∴DE∥BF,
∴△EDM∽△FBM,
(2):解:
∵△EDM∽△FBM,
x
2x
解:∵DE∥AC,
6-x
22.2相似三角形的判定(第1课时)
本节课内容:
1.认识相似三角形,知道相似三角形的表示方
法及相似比.
2.学习一个定理:相似三角形判定的预备定理.
1.认识相似三角形:
回顾:什么样的两个多边形是相似多边形?
相似多边形:
边数相同
对应角相等
对应边长度的比相等
相似三角形:
对应角相等
对应边长度的比相等
相似三角形
1.定义:
对应角相等,三边对应成比例的两个三角形相似.
符号语言:
∵∠A=∠A′,∠B=∠B′,∠C=∠C′,
∴△ABC∽△A′B′C′
AB:BC:CA=A′B′:B′C′:C′A′
2.
相似三角形的表示:
2.相似三角形的表示:
符号:“∽”,
读作:相似于
两个三角形相似,用相似符号表示时,与全等一样,应把对应顶点的字母写在对应的位置上.
△ABC相似于△A′B′C′
这样便于找出相似三角形的
对应角和对应边.
如图,记作:△ABC∽△A′B′C′
注意:写成△ABC∽△A′B′C′,表明对应关系是唯一确定的,
即A与A′、B与B′、C与C′分别对应.如果仅说“△ABC相似于△A′B′C′
没有用“∽”表示的,则没有说明对应关系.
3.
相似三角形的相似比:
3.相似三角形的相似比:
△ABC∽△A′B′C′
相似三角形的对应边的比相似比.
注意:相似比的表述有顺序性
△ABC
与△A′B′C′
的相似比为k1:.
.
△A′B′C′与△ABC
的相似比为k2
.
显然,
k1
·
k2
=1
显然,当且仅当三角形全等时
k1
=k2
=1
相似三角形基本性质:
相似三角形的对应角相等,三边对应成比例
符号语言:
∵△ABC∽△A′B′C′
∴∠A=∠A′,∠B=∠B′,∠C=∠C′,
认识:
根据三角形相似,利用其性质是解决角和线段问题的重要方法!
4.相似三角形判定的预备定理:
温故知新:
平行线分线段成比例定理的推论?
推论:平行于三角形一边的直线和其他两边
(或两边延长线)相交,截得的对应线段成比例
A
C
B
F
E
A
F
E
C
B
EF∥BC
大胆猜测:
△AEF与△ABC相似
平行于三角形一边的直线和其他两边(或两边的延长线)
相交,截的三角形与原三角形相似。
求证:
已知:DE//BC
求证:△ADE∽△ABC
1.根据相似三角形的定义△ADE与
△ABC相似必须满足哪些条件?
分析:
∠A=∠A,∠ADE=∠B,
∠
AED=∠C,
2.已经具备哪些条件?为什么?还需要什么条件?
已有条件:∠A=∠A,∠ADE=∠B,
∠AED=∠C
,
A
D
B
C
E
A
E
A
C
E
A
C
E
A
B
C
E
A
D
B
C
A
图2
还需条件:
分析:
3.关键:
A
D
E
B
C
启发:将DE平移到BC上
此时,DF∥AC
F
类比、转化思想!
实际作图,我们作DF∥AC
已知:DE//BC
求证:△ADE∽△ABC
证明:
F
作DF∥AC,交BC于点F
则DE=FC,
∵DE∥BC,
∴∠A=∠A,∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC
E
D
A
C
B
已知:DE//BC
求证:△ADE∽△ABC
F
证明:
作DF∥EC,交BC延长线于点F
∵DE∥BC,
∴△ADE∽△ABC
则DE=FC,
∴∠EAD=∠BAC,∠ADE=∠B,∠AED=∠ACB,
E
D
A
C
B
已知:DE//BC
求证:△ADE∽△ABC
F
证明:
在AB上截取AF=AE
G
作FG∥BC,交AC于点G
由前面结论,得△AFG∽△ABC
∵DE∥BC,
∴DE∥FG,
∴∠D=∠AFG,∠E=∠AGF,
∴△ADE≌△AFG
∴△ADE∽△ABC
E
D
A
C
B
∵DE∥BC,
∴△ADE∽△ABC
平行于三角形一边的直线和其他两边(或两边的延长线)
相交,截的三角形与三角形相似。
相似三角形判定的预备定理
符号语言:
“A”型
“X”型
E
D
A
C
B
∵DE∥BC,
∴△ADE∽△ABC
线段必须是边
例题巩固:
注意:
根据两个定理和推论,利用平行线得到线段成比例,是解决线段问题的重要方法!
教材P78.练习:
F
DE∥BC,
DF∥AC,
判断正误:
巩固练习
如图,在
ABCD中,DE交BC于F,交AB的延长线于点E.
(1)请写出图中相似的三角形;
(2)请由其中的一对相似三角形写出相应的比例式;
F
A
B
C
D
E
△CDF∽
△BEF
,
△BEF∽△AED
△CDF∽△AED
也可写成
△BEF∽△CDF∽△AED
(1)∵DE∥BC,
∴△ADE∽△ABC
(2)∵DE∥BC,
5EC=12
EC=2.4
2
3
4
6
4
∵CF=BF
如图,△ABC中BD是角平分线,过点D作DE∥AB交BC于E,AB=5cm,
BE=3cm,求EC的长.
A
B
C
D
E
1
2
5
3
x
解:∵DE∥AB,
∠2=∠3
3
∵∠1=∠2
∴∠1=∠3
∴DE=BE=3
3(x+3)=5x
x=4.5
∴△CDE∽△CAB
(1):证明:∵AB=2EB,
AB=2DC,
∴EB=DC,
又,BE∥DC,
∴四边形BCDE是平行四边形
∴DE∥BF,
∴△EDM∽△FBM,
(2):解:
∵△EDM∽△FBM,
x
2x
解:∵DE∥AC,
6-x
