六年级数学下册 一课一练《总复习-图形与几何》习题2-北师大版(含答案)
文档属性
| 名称 | 六年级数学下册 一课一练《总复习-图形与几何》习题2-北师大版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 262.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 10:31:29 | ||
图片预览




文档简介
《总复习-图形与几何》习题2
一、选择题
1.如图,大正方形的面积是10平方厘米,依次连接正方形各边的中点,那么,大圆与小正方形的面积比是( )
A.2π:1
B.4:1
C.π:1
D.8:1
2.在学习三角形的特征时,3名同学分别选取了3根小棒如图,则可以围成三角形的是( )
A.
B.
C.
3.角的两边是两条( )
A.直线
B.线段
C.射线
4.下面说法正确的有( )句.
①正方形和长方形都是特殊的平行四边形.
②一个三角形三个内角的度数比是1:1:2,这一定是一个等腰直角三角形.
③57和76的公因数只有1.
④钟表上分针转动的速度是时针的60倍.
⑤两个连续自然数的积一定是合数.
A.1
B.2
C.3
D.4
5.下面( )组中的三条线段可以围成一个三角形.
A.5cm、6cm、7cm
B.5cm、5cm、10cm
C.3cm、8cm、4cm
6.在三角形中,若∠1+∠2=∠3,那么这个三角形是( )三角形.
A.锐角
B.直角
C.钝角
D.等边
7.一个三角形最小的内角是55°,这个三角形一定是( )三角形.
A.锐角
B.直角
C.钝角
D.等边
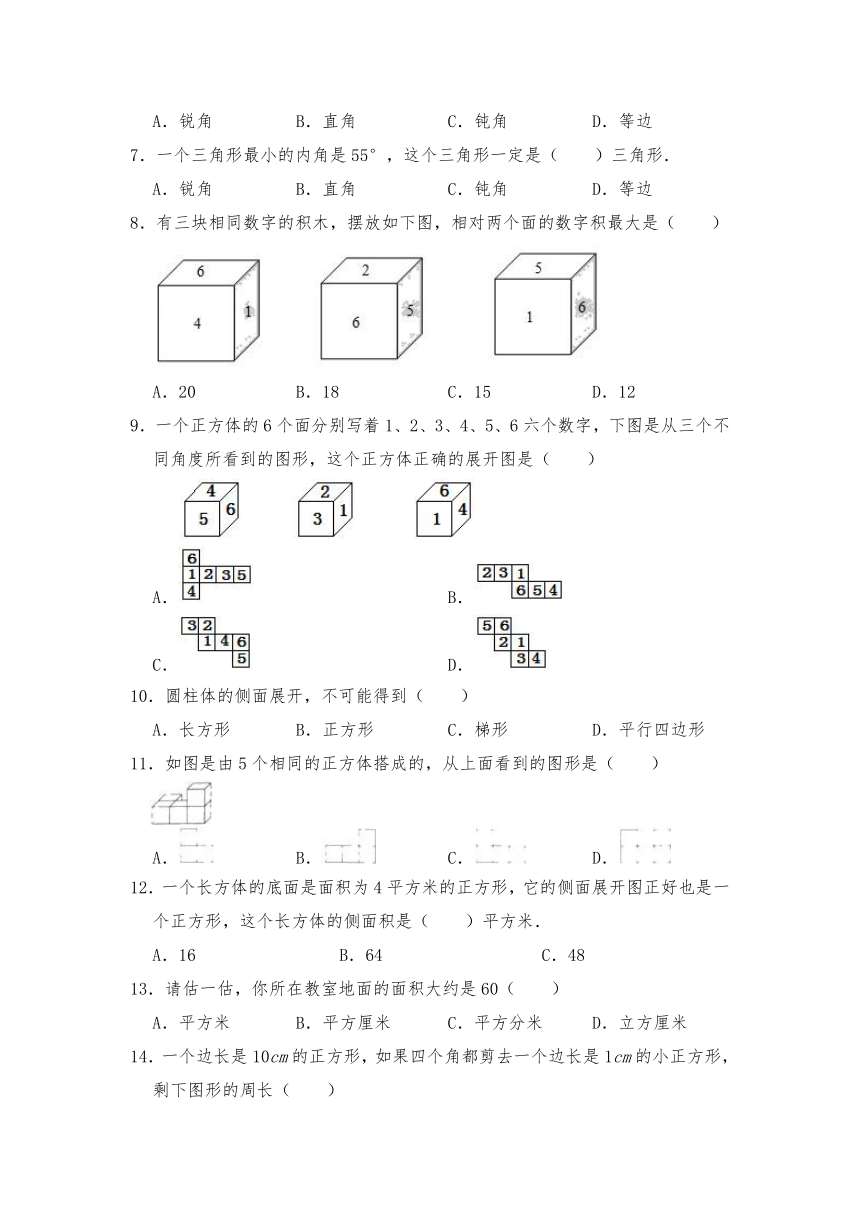
8.有三块相同数字的积木,摆放如下图,相对两个面的数字积最大是( )
A.20
B.18
C.15
D.12
9.一个正方体的6个面分别写着1、2、3、4、5、6六个数字,下图是从三个不同角度所看到的图形,这个正方体正确的展开图是( )
A.
B.
C.
D.
10.圆柱体的侧面展开,不可能得到( )
A.长方形
B.正方形
C.梯形
D.平行四边形
11.如图是由5个相同的正方体搭成的,从上面看到的图形是( )
A.
B.
C.
D.
12.一个长方体的底面是面积为4平方米的正方形,它的侧面展开图正好也是一个正方形,这个长方体的侧面积是( )平方米.
A.16
B.64
C.48
13.请估一估,你所在教室地面的面积大约是60( )
A.平方米
B.平方厘米
C.平方分米
D.立方厘米
14.一个边长是10cm的正方形,如果四个角都剪去一个边长是1cm的小正方形,剩下图形的周长( )
A.增加4cm
B.减少4cm
C.与原来相等
D.以上答案都不对
15.下列图中的四个正方形的边长均相等,其中阴影部分面积最大的图形是( )
A.
B.
C.
D.
16.一根彩绳和A、B、C三个钉子围成如图的三角形,如果将三角形一角顶点处的钉子去掉,并将这条彩绳钉成一个长方形,则所钉成的长方形的面积是( )
A.7或15
B.16或15
C.7或15或16
D.无数个答案
17.圆柱体积公式推导:把圆柱的底面分成许多相等的扇形,然后把它切开拼成一个近似的长方体,这个近似长方体的底面积等于圆柱的底面积,高等于圆柱的高……这个推导过程蕴含了( )的数学思想.
A.一一对应
B.数形结合
C.类比归纳
D.转化
二、填空题
1.在钟面上,分针转动一周,时针转动的角度是
度.
2.(单位:cm)以直角三角形的长直角边为轴旋转一周(如图)得到几何体是
,体积是
cm3.
3.观察下面用4个正方体搭成的图形,并填一填.
(1)从正面看到的图形是的有
.
(2)从侧面看到的图形是的有
.
(3)从上面看到的图形是的有
.
4.用8个棱长2厘米的立方体拼成长方体或大立方体(全部都要用上),拼成图形的棱长总和最小是
厘米,最大是
厘米.
5.有一根半径是2厘米,高是6厘米的圆柱形钢材,加工成与它等底等高的圆锥,要切去
立方厘米的钢材.
6.4平方米=
平方分米
8平方米30平方分米=
平方分米
307平方厘米=
平方分米
平方厘米.
7.在一张长12厘米、宽10厘米的彩纸上画一个最大的圆,这个圆的周长是
厘米,面积是
平方厘米.
三、判断题
1.直线没有端点.(判断对错)
2.角的两边越长,角的度数越大.(
)
3.任意一个四边形的内角和一定是360度.(
)
4.直径是圆内最长的线段.(
)
5.任意一个圆的周长与它的直径的比值是3.14.(
)
6.圆的周长总是它直径的π倍.
(
)
7.圆柱和圆锥的高都只有一条.(
)
8.一个圆柱的底面半径是8厘米,它的侧面展开图正好是一个正方形,这个圆柱的高是16厘米(
)
9.用4个圆心角都是90°的扇形,一定可以拼成一个圆.(
)
四、计算题
1.求如图阴影部分的周长和面积.
2.求阴影部分的周长.(单位:厘米)
五、应用题
1.如图,等腰直角三角形ABC和四分之一圆DEB,已知AB=5厘米,BE=2厘米,求图中阴影部分的面积。
2.如图是爸爸制作一个圆柱形油桶的资料图,阴影部分是制作油桶所用的铁皮,空白部分为边角料,请你根据右图计算这个油桶的容积是多少升.(接头处忽略不计,Π取3.14)
3.(1)在如图的水缸内拿走一架体积是360cm3的玩具车后,水位比之前下降了多少厘米?
(2)制作这个无盖的玻璃水缸,至少需要多大面积的玻璃?
六、操作题
1.如图,以长方形或三角形的一条边为轴旋转一周,会形成相应的立体图形,请用线连一连.
2.画出下面大人在路灯下的影子.
3.分别画出下面立体图形从正面、上面、左面看到的图形.
4.画一个周长为12.56厘米的圆.
七、解答题
1.画出下列图形底边上的高.
2.把下面这个展开图折成一个长方体.
(1)如果C面在底部,那么
面在上面.
(2)如果F面在前面,从左面看是B面,那么
面在上面.
(3)如果要求这个长方体的表面积和体积,至少要量出哪些边的长度?
3.同学们都知道三角形内角和是180°,四边形内角和是360°,请你求出99边形的内角和。
4.图中,直径为3厘米的半圆绕A逆时针旋转60°使AB到达AC的位置,求图中阴影部分的周长.
答案
一、选择题
1.C.2.B.3.C.4.B.5.A.6.B.7.A.8.A.
9.D.10.C.11.C。12.B。13.A.14.C.
15.B。16.C.17.D。
二、填空题
1.30.
2.圆锥体,37.68.
3.(3),(1)、(3)、(4),(1)、(4).
4.48,80.
5.50.24.
6.400,830,3,7.
7.31.4、78.5.
三、判断题
1.√.2.×.3.√4.√.5.×.6.√7.×.8.×.9.×.
四、计算题
1.解:周长:3.14×4×1.5+4
=18.84+4
=22.84(厘米)
面积:3.14×(4÷2)2÷2
=3.14×2
=6.28(平方厘米)
答:阴影部分的周长是22.84厘米,面积是6.28平方厘米.
2.解:3.14×10+10×2
=31.4+20
=51.4(厘米)
答:阴影部分的周长是51.4厘米.
五、应用题
1.解:5×5÷2﹣3.14×22÷4
=12.5﹣3.14
=9.36(平方厘米)
答:图中阴影部分的面积9.36平方厘米。
2.解:设圆的直径为d分米
d+πd=16.56
4.14d=16.56
4.14d÷4.14=16.56÷4.14
d=4
3.14×(4÷2)2×(4×2)
=3.14×4×8
=12.56×8
=100.48(立方分米)
100.48立方分米=100.48升
答:这个油桶的容积是100.48升。
3.解:(1)水位下降的高度为:
360÷(20×12)
=360÷240
=1.5(cm)
答:水位比之前下降了1.5厘米.
(2)需要玻璃的面积为:
15×20×2+15×12×2+20×12
=300×2+180×2+240
=600+360+240
=960+240
=1200(cm2)
答:至少需要1200平方厘米的玻璃.
六、操作题
1.解:长方形或三角形右面的一条边为轴,旋转一周,得到如下图形:
2.解:画出下面大人在路灯下的影子:
3.解:根据题干分析可得:
4.解:12.56÷3.14÷2=2(厘米)
作图如下:
七、解答题
1.解:作平行四边形、三角形的高如下:
2.E;C.
3.解:从四边形的一个顶点可以引出1条对角线,把四边形分成2个三角形,那么它的内角和是180°×2=360°,
从五边形的一个顶点可以引出2条对角线,把五边形分成3个三角形,那么它的内角和是180°×3=540°,
从六边形的一个顶点可以引出3条对角线,把六边形分成4个三角形,那么它的内角和是180°×4=720°,
…
从n(n大于或等于3)边形的一个顶点可以引出(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,那么n边形的内角和为180°×(n﹣2),
当n=99时,
180°×(99﹣2)
=180°×97
=17460°
答:99边形的内角和是17460°。
4.解:3.14×3+3.14×3,
=9.42+3.14,
=12.56(厘米);
答:阴影部分的周长是12.56厘米.
一、选择题
1.如图,大正方形的面积是10平方厘米,依次连接正方形各边的中点,那么,大圆与小正方形的面积比是( )
A.2π:1
B.4:1
C.π:1
D.8:1
2.在学习三角形的特征时,3名同学分别选取了3根小棒如图,则可以围成三角形的是( )
A.
B.
C.
3.角的两边是两条( )
A.直线
B.线段
C.射线
4.下面说法正确的有( )句.
①正方形和长方形都是特殊的平行四边形.
②一个三角形三个内角的度数比是1:1:2,这一定是一个等腰直角三角形.
③57和76的公因数只有1.
④钟表上分针转动的速度是时针的60倍.
⑤两个连续自然数的积一定是合数.
A.1
B.2
C.3
D.4
5.下面( )组中的三条线段可以围成一个三角形.
A.5cm、6cm、7cm
B.5cm、5cm、10cm
C.3cm、8cm、4cm
6.在三角形中,若∠1+∠2=∠3,那么这个三角形是( )三角形.
A.锐角
B.直角
C.钝角
D.等边
7.一个三角形最小的内角是55°,这个三角形一定是( )三角形.
A.锐角
B.直角
C.钝角
D.等边
8.有三块相同数字的积木,摆放如下图,相对两个面的数字积最大是( )
A.20
B.18
C.15
D.12
9.一个正方体的6个面分别写着1、2、3、4、5、6六个数字,下图是从三个不同角度所看到的图形,这个正方体正确的展开图是( )
A.
B.
C.
D.
10.圆柱体的侧面展开,不可能得到( )
A.长方形
B.正方形
C.梯形
D.平行四边形
11.如图是由5个相同的正方体搭成的,从上面看到的图形是( )
A.
B.
C.
D.
12.一个长方体的底面是面积为4平方米的正方形,它的侧面展开图正好也是一个正方形,这个长方体的侧面积是( )平方米.
A.16
B.64
C.48
13.请估一估,你所在教室地面的面积大约是60( )
A.平方米
B.平方厘米
C.平方分米
D.立方厘米
14.一个边长是10cm的正方形,如果四个角都剪去一个边长是1cm的小正方形,剩下图形的周长( )
A.增加4cm
B.减少4cm
C.与原来相等
D.以上答案都不对
15.下列图中的四个正方形的边长均相等,其中阴影部分面积最大的图形是( )
A.
B.
C.
D.
16.一根彩绳和A、B、C三个钉子围成如图的三角形,如果将三角形一角顶点处的钉子去掉,并将这条彩绳钉成一个长方形,则所钉成的长方形的面积是( )
A.7或15
B.16或15
C.7或15或16
D.无数个答案
17.圆柱体积公式推导:把圆柱的底面分成许多相等的扇形,然后把它切开拼成一个近似的长方体,这个近似长方体的底面积等于圆柱的底面积,高等于圆柱的高……这个推导过程蕴含了( )的数学思想.
A.一一对应
B.数形结合
C.类比归纳
D.转化
二、填空题
1.在钟面上,分针转动一周,时针转动的角度是
度.
2.(单位:cm)以直角三角形的长直角边为轴旋转一周(如图)得到几何体是
,体积是
cm3.
3.观察下面用4个正方体搭成的图形,并填一填.
(1)从正面看到的图形是的有
.
(2)从侧面看到的图形是的有
.
(3)从上面看到的图形是的有
.
4.用8个棱长2厘米的立方体拼成长方体或大立方体(全部都要用上),拼成图形的棱长总和最小是
厘米,最大是
厘米.
5.有一根半径是2厘米,高是6厘米的圆柱形钢材,加工成与它等底等高的圆锥,要切去
立方厘米的钢材.
6.4平方米=
平方分米
8平方米30平方分米=
平方分米
307平方厘米=
平方分米
平方厘米.
7.在一张长12厘米、宽10厘米的彩纸上画一个最大的圆,这个圆的周长是
厘米,面积是
平方厘米.
三、判断题
1.直线没有端点.(判断对错)
2.角的两边越长,角的度数越大.(
)
3.任意一个四边形的内角和一定是360度.(
)
4.直径是圆内最长的线段.(
)
5.任意一个圆的周长与它的直径的比值是3.14.(
)
6.圆的周长总是它直径的π倍.
(
)
7.圆柱和圆锥的高都只有一条.(
)
8.一个圆柱的底面半径是8厘米,它的侧面展开图正好是一个正方形,这个圆柱的高是16厘米(
)
9.用4个圆心角都是90°的扇形,一定可以拼成一个圆.(
)
四、计算题
1.求如图阴影部分的周长和面积.
2.求阴影部分的周长.(单位:厘米)
五、应用题
1.如图,等腰直角三角形ABC和四分之一圆DEB,已知AB=5厘米,BE=2厘米,求图中阴影部分的面积。
2.如图是爸爸制作一个圆柱形油桶的资料图,阴影部分是制作油桶所用的铁皮,空白部分为边角料,请你根据右图计算这个油桶的容积是多少升.(接头处忽略不计,Π取3.14)
3.(1)在如图的水缸内拿走一架体积是360cm3的玩具车后,水位比之前下降了多少厘米?
(2)制作这个无盖的玻璃水缸,至少需要多大面积的玻璃?
六、操作题
1.如图,以长方形或三角形的一条边为轴旋转一周,会形成相应的立体图形,请用线连一连.
2.画出下面大人在路灯下的影子.
3.分别画出下面立体图形从正面、上面、左面看到的图形.
4.画一个周长为12.56厘米的圆.
七、解答题
1.画出下列图形底边上的高.
2.把下面这个展开图折成一个长方体.
(1)如果C面在底部,那么
面在上面.
(2)如果F面在前面,从左面看是B面,那么
面在上面.
(3)如果要求这个长方体的表面积和体积,至少要量出哪些边的长度?
3.同学们都知道三角形内角和是180°,四边形内角和是360°,请你求出99边形的内角和。
4.图中,直径为3厘米的半圆绕A逆时针旋转60°使AB到达AC的位置,求图中阴影部分的周长.
答案
一、选择题
1.C.2.B.3.C.4.B.5.A.6.B.7.A.8.A.
9.D.10.C.11.C。12.B。13.A.14.C.
15.B。16.C.17.D。
二、填空题
1.30.
2.圆锥体,37.68.
3.(3),(1)、(3)、(4),(1)、(4).
4.48,80.
5.50.24.
6.400,830,3,7.
7.31.4、78.5.
三、判断题
1.√.2.×.3.√4.√.5.×.6.√7.×.8.×.9.×.
四、计算题
1.解:周长:3.14×4×1.5+4
=18.84+4
=22.84(厘米)
面积:3.14×(4÷2)2÷2
=3.14×2
=6.28(平方厘米)
答:阴影部分的周长是22.84厘米,面积是6.28平方厘米.
2.解:3.14×10+10×2
=31.4+20
=51.4(厘米)
答:阴影部分的周长是51.4厘米.
五、应用题
1.解:5×5÷2﹣3.14×22÷4
=12.5﹣3.14
=9.36(平方厘米)
答:图中阴影部分的面积9.36平方厘米。
2.解:设圆的直径为d分米
d+πd=16.56
4.14d=16.56
4.14d÷4.14=16.56÷4.14
d=4
3.14×(4÷2)2×(4×2)
=3.14×4×8
=12.56×8
=100.48(立方分米)
100.48立方分米=100.48升
答:这个油桶的容积是100.48升。
3.解:(1)水位下降的高度为:
360÷(20×12)
=360÷240
=1.5(cm)
答:水位比之前下降了1.5厘米.
(2)需要玻璃的面积为:
15×20×2+15×12×2+20×12
=300×2+180×2+240
=600+360+240
=960+240
=1200(cm2)
答:至少需要1200平方厘米的玻璃.
六、操作题
1.解:长方形或三角形右面的一条边为轴,旋转一周,得到如下图形:
2.解:画出下面大人在路灯下的影子:
3.解:根据题干分析可得:
4.解:12.56÷3.14÷2=2(厘米)
作图如下:
七、解答题
1.解:作平行四边形、三角形的高如下:
2.E;C.
3.解:从四边形的一个顶点可以引出1条对角线,把四边形分成2个三角形,那么它的内角和是180°×2=360°,
从五边形的一个顶点可以引出2条对角线,把五边形分成3个三角形,那么它的内角和是180°×3=540°,
从六边形的一个顶点可以引出3条对角线,把六边形分成4个三角形,那么它的内角和是180°×4=720°,
…
从n(n大于或等于3)边形的一个顶点可以引出(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,那么n边形的内角和为180°×(n﹣2),
当n=99时,
180°×(99﹣2)
=180°×97
=17460°
答:99边形的内角和是17460°。
4.解:3.14×3+3.14×3,
=9.42+3.14,
=12.56(厘米);
答:阴影部分的周长是12.56厘米.
