六年级数学下册 一课一练《总复习-图形与几何》习题3-北师大版(含答案)
文档属性
| 名称 | 六年级数学下册 一课一练《总复习-图形与几何》习题3-北师大版(含答案) | 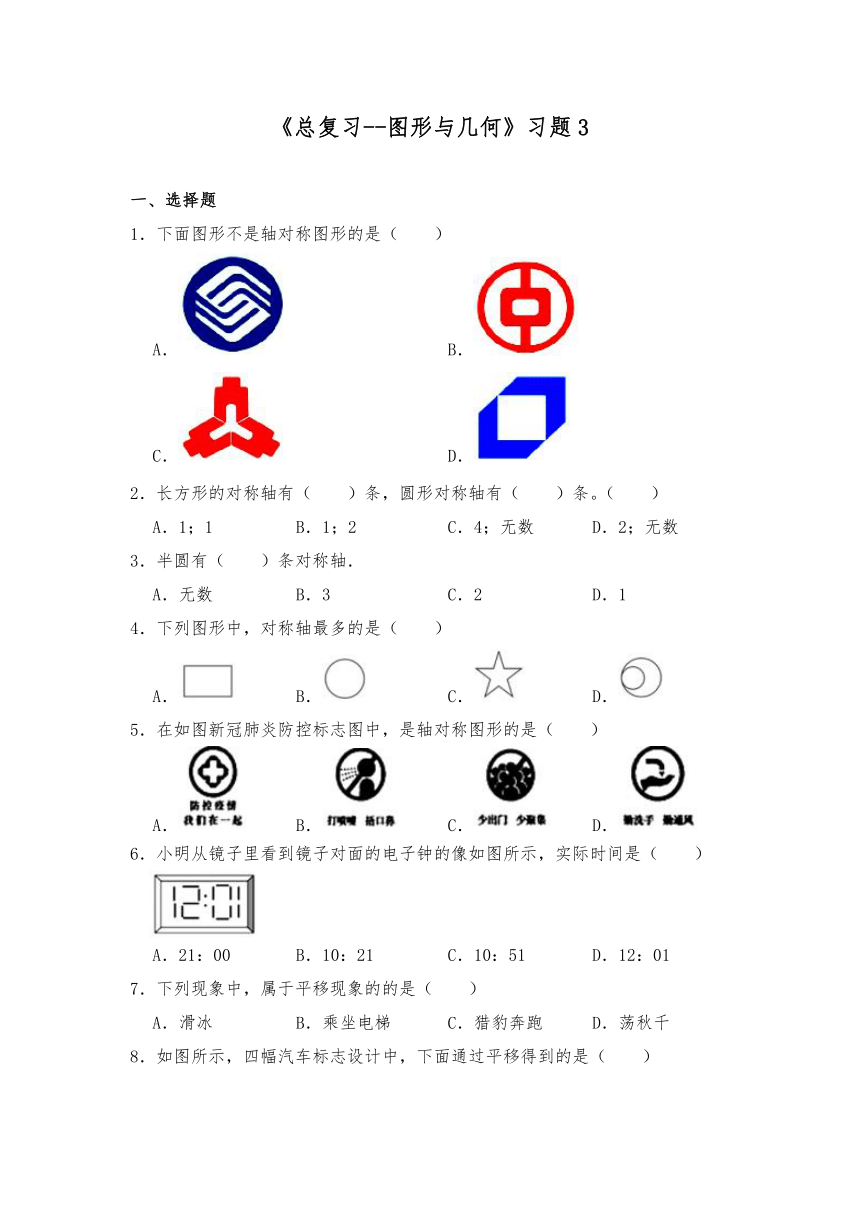 | |
| 格式 | zip | ||
| 文件大小 | 642.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 10:31:59 | ||
图片预览



文档简介
《总复习--图形与几何》习题3
一、选择题
1.下面图形不是轴对称图形的是( )
A.
B.
C.
D.
2.长方形的对称轴有( )条,圆形对称轴有( )条。( )
A.1;1
B.1;2
C.4;无数
D.2;无数
3.半圆有( )条对称轴.
A.无数
B.3
C.2
D.1
4.下列图形中,对称轴最多的是( )
A.
B.
C.
D.
5.在如图新冠肺炎防控标志图中,是轴对称图形的是( )
A.
B.
C.
D.
6.小明从镜子里看到镜子对面的电子钟的像如图所示,实际时间是( )
A.21:00
B.10:21
C.10:51
D.12:01
7.下列现象中,属于平移现象的的是( )
A.滑冰
B.乘坐电梯
C.猎豹奔跑
D.荡秋千
8.如图所示,四幅汽车标志设计中,下面通过平移得到的是( )
A.
B.
C.
D.
9.火车在铁轨上运动,车轮的运动是( )
A.旋转
B.平移
C.轴对称
D.既平移又旋转
10.将图案绕P点逆时针旋转90度,得到的图案是( )
A.
B.
C.
11.如图,长方形是按一定的比例放大或缩小,则x=( )
A.10
B.12
C.14
D.16
12.小华将一张正方形纸对折后剪去一个(如图),展开后是图( )
A.
B.
C.
D.
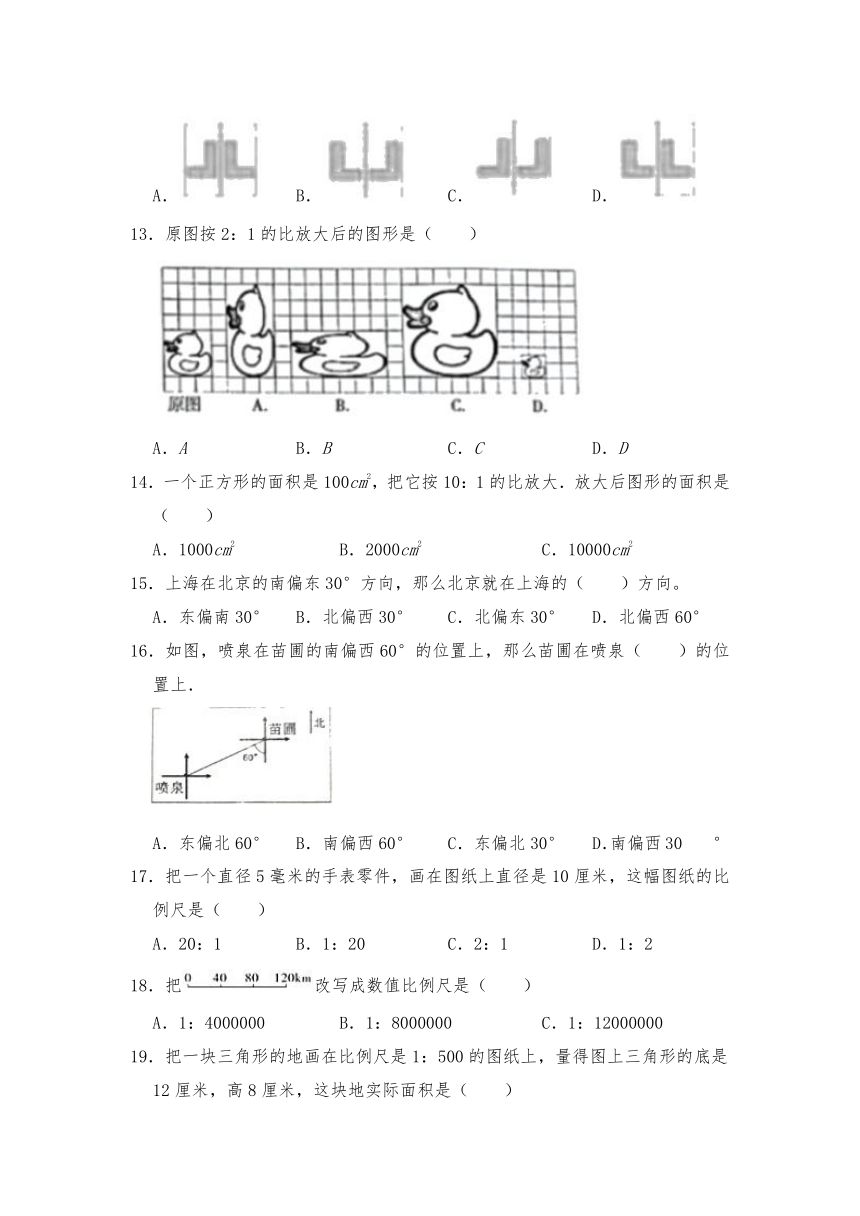
13.原图按2:1的比放大后的图形是( )
A.A
B.B
C.C
D.D
14.一个正方形的面积是100cm2,把它按10:1的比放大.放大后图形的面积是( )
A.1000cm2
B.2000cm2
C.10000cm2
15.上海在北京的南偏东30°方向,那么北京就在上海的( )方向。
A.东偏南30°
B.北偏西30°
C.北偏东30°
D.北偏西60°
16.如图,喷泉在苗圃的南偏西60°的位置上,那么苗圃在喷泉( )的位置上.
A.东偏北60°
B.南偏西60°
C.东偏北30°
D.南偏西30°
17.把一个直径5毫米的手表零件,画在图纸上直径是10厘米,这幅图纸的比例尺是( )
A.20:1
B.1:20
C.2:1
D.1:2
18.把改写成数值比例尺是( )
A.1:4000000
B.1:8000000
C.1:12000000
19.把一块三角形的地画在比例尺是1:500的图纸上,量得图上三角形的底是12厘米,高8厘米,这块地实际面积是( )
A.480平方米
B.240平方米
C.1200平方米
D.2400
平方米
二、填空题
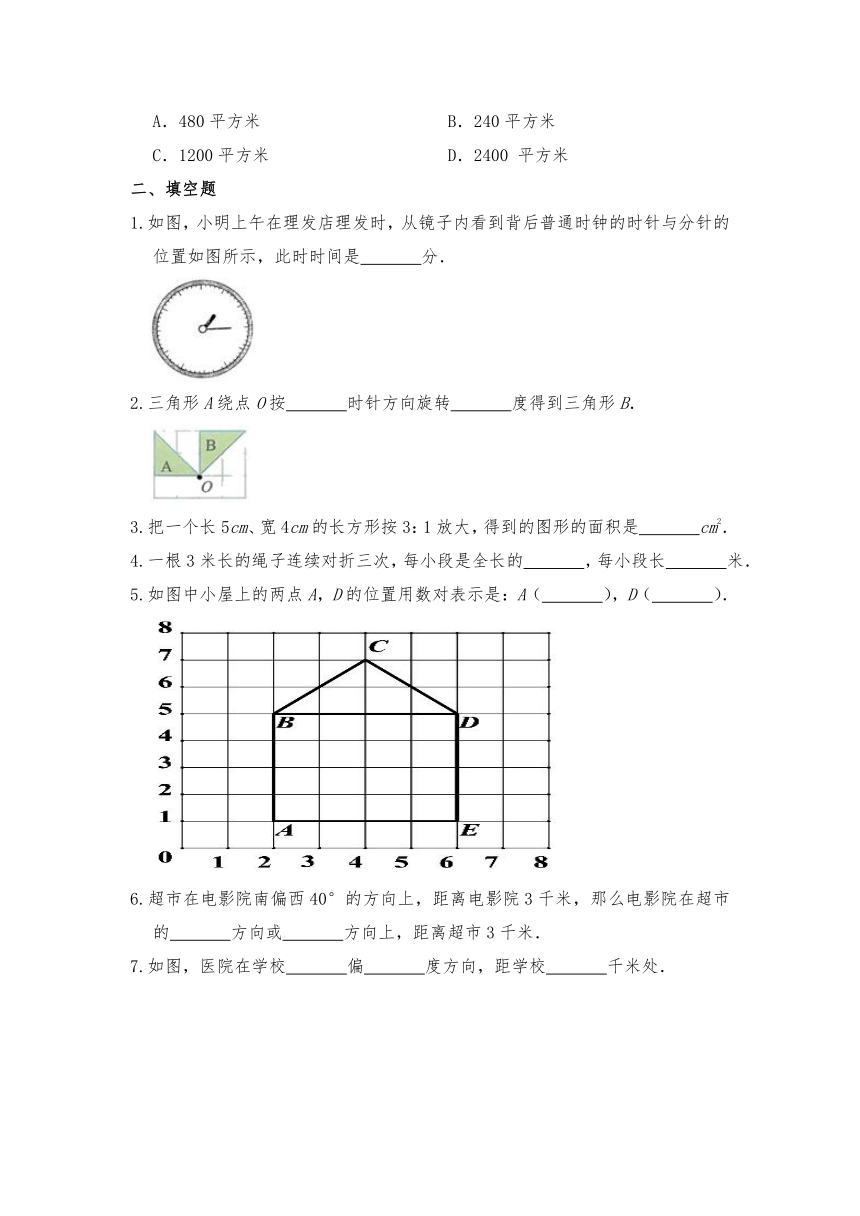
1.如图,小明上午在理发店理发时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是
分.
2.三角形A绕点O按
时针方向旋转
度得到三角形B.
3.把一个长5cm、宽4cm的长方形按3:1放大,得到的图形的面积是
cm2.
4.一根3米长的绳子连续对折三次,每小段是全长的
,每小段长
米.
5.如图中小屋上的两点A,D的位置用数对表示是:A(
),D(
).
6.超市在电影院南偏西40°的方向上,距离电影院3千米,那么电影院在超市的
方向或
方向上,距离超市3千米.
7.如图,医院在学校
偏
度方向,距学校
千米处.
8.如图,小玲在小明的西偏北60°方向上,则小明在小玲的
偏
°方向上.
9.一幅地图的比例尺是1:3000000,这幅地图上两个城市之间的距离是20cm,那么这两个城市之间的实际距离是
km.
10.在一幅比例尺是1:500000的地图上量得郑州到开封的距离是15.6cm.郑州到开封的实际距离是
km.一辆汽车在9时15分从郑州出发,以每小时65km的速度行驶,预计
时
分可以到达开封.
11.看图填空.
某路公共汽车从机场到图书馆的行驶路线是:向
行驶
站到红星广场,再向
行驶
站到动物园,再向
行驶
站到图书馆.
三、应用题
1.一幅地图的比例尺是1:6000000,在这幅地图上量得A地到B地的距离是9.6cm。一辆汽车从A地开往B地,每时行80km,多少小时能到达?
2.在比例尺为1:50000000的地图上,量得甲乙两地的距离是8厘米,一架飞机从甲地飞往乙地用4小时,这架飞机平均每小时飞行多少千米?
3.荆州城,曾名为“江陵城”,“千里江陵一日还”说的就是荆州城.荆州城现存明清重建城墙东西长3.75千米,在比例尺是1:20000的地图上长度约是多少厘米?在这幅地图上量得城墙南北最宽相距6厘米,南北的实际距离是多少千米?
4.在比例尺为1:500000的地图上,量得A.B两地的图上距离是6cm,一辆汽车上午8时从A地以90千米/时的速度开往B地,到达B地的时间是几时?
四、操作题
1.(1)画出图形①的轴对称图形.
(2)画出把三角形AOB向下平移6个格后的三角形A′O′B′.
(3)画出三角形AOB绕B点逆时针旋转90°后的图形.
2.按要求画图(每个小方格边长表示1cm).
(1)把图A补全,使它成为一个轴对称图形.
(2)把图B先向右平移6格,再向上平移3格.
(3)把图C绕点O按顺时针方向旋转90°.
(4)画出图D按3:1的比放大后的图形.
3.按要求在方格纸中作图.
①根据给定的对称轴画出图形A的另一半.
②画出图形B向右平移4格后的图形.
③画出将图形C按2:1放大后的图形.
4.在方格纸上按要求画出图形.
(1)图形A向右平移5格得到图形B.
(2)图形B绕平移后的点O1,顺时针旋转90°,得到图形C.
(3)画出图形C关于直线L的对称图形D.
5.
6.按要求在如图的点子图中画图.
(1)三角形A绕点O逆时针旋转90°得到图形B.
(2)图形B向右平移5个单位得到图形C.
(3)请将三角形A按1:2缩小画在点子图上.
7.在图中完成下列问题.
(1)科技馆在学校北偏东30°方向200米处.请在图中标出科技馆的位置,并标出图上距离.
(2)南京路经过电影院,与上海路平行.请用直线标出南京路的位置.
8.小芳家要修一条小路到公路上,该怎样修最近?在图中画出来.
9.按要求做题.图中1个小方格的面积为1平方厘米.
(1)把三角形绕点B逆时针旋转90o,画出旋转后的图形.
(2)标出点D(2,2)和点E(6,2)的位置.
(3)以DE为下底,画一个上底为2厘米,高为3厘米的等腰梯形.
(4)画出的梯形的面积是
平方厘米.
答案
一、选择题
1.A。2.D。3.D.4.B.5.A.6.C.7.B.8.A.9.A.
10.B.11.B.12.A.13.C.14.C.15.B。16.C。
17.A。18.A.19.C.
二、填空题
1.10时45.
2.顺,90.
3.180.
4.;.
5.2,1;6,5.
6.北偏东40°方向;东偏北50°.
7.北,西30,6.
8.东,南,60.
9.600。
10.78,10,27.
11.东,1,东北,1,北,3.
三、应用题
1.解:9.6
=9.6×6000000
=57600000(厘米)
57600000厘米=576千米
576÷80=7.2(小时)
答:7.2小时到达。
2.解:8400000000(厘米)
400000000厘米=4000千米
4000÷4=1000(千米)
答:这架飞机平均每小时飞行1000千米。
3.解:3.75千米=375000厘米
37500018.75(厘米)
6120000(厘米)
120000厘米=1.2千米
答:在比例尺是1:20000的地图上长度约是18.75厘米,南北的实际距离是1.2千米.
4.解:63000000(厘米)
3000000厘米=30千米
30÷90(小时)=20(分钟)
8时+20分钟=8时20分
答:辆汽车上午8时从A地以90千米/时的速度开往B地,到达B地的时间是8时20分.
四、操作题
1.解:(1)画出图形①的轴对称图形(图形②).
(2)画出把三角形AOB向下平移6个格后的三角形A′O′B′.
(3)画出三角形AOB绕B点逆时针旋转90°后的图形(三角形A″O″B).
2.解:(1)把图A补全,使它成为一个轴对称图形(图中红色部分).
(2)把图B先向右平移6格,再向上平移3格(图中绿色部分).
(3)把图C绕点O按顺时针方向旋转90°(图中黄色部分).
(4)画出图D按3:1的比放大后的图形(图中蓝色部分).
3.解:①根据给定的对称轴画出图形A的另一半(图形A′).
②画出图形B向右平移4格后的图形图形B′).
③画出将图形C按2:1放大后的图形(图形C′).
4.解:(1)图形A向右平移5格得到图形B(图中红色部分).
(2)图形B绕平移后的点O1,顺时针旋转90°,得到图形C(图中绿色部分).
(3)画出图形C关于直线L的对称图形D(图中蓝色部分).
5.解:
6.解:(1)三角形A绕点O逆时针旋转90°得到图形B(下图红色部分).
(2)图形B向右平移5个单位得到图形C(下图绿色部分).
(3)请将三角形A按1:2缩小画在点子图上(图形D,下图蓝色部分).
7.解:(1)科技馆离学校实际距离200米,由比例尺1:10000得:
200米=20000厘米
20000÷10000=2(厘米)
所以科技馆到学校的图上距离是2厘米.
科技馆在学校北偏东30°方向200米处.(作图如下)
(2)南京路经过电影院,与上海路平行.用直线标出南京路的位置.(如图)
8.解:
9.解:(1)把三角形绕点B逆时针旋转90o,画出旋转后的图形(三角形A′BC′).
(2)标出点D(2,2)和点E(6,2)的位置(下图).
(3)以DE为下底,画一个上底为2厘米,高为3厘米的等腰梯形(等腰梯形DEFG).
(4)画出的梯形的面积是:
(2+4)×3
=6×3
=9(平方厘米).
故答案为:9.
一、选择题
1.下面图形不是轴对称图形的是( )
A.
B.
C.
D.
2.长方形的对称轴有( )条,圆形对称轴有( )条。( )
A.1;1
B.1;2
C.4;无数
D.2;无数
3.半圆有( )条对称轴.
A.无数
B.3
C.2
D.1
4.下列图形中,对称轴最多的是( )
A.
B.
C.
D.
5.在如图新冠肺炎防控标志图中,是轴对称图形的是( )
A.
B.
C.
D.
6.小明从镜子里看到镜子对面的电子钟的像如图所示,实际时间是( )
A.21:00
B.10:21
C.10:51
D.12:01
7.下列现象中,属于平移现象的的是( )
A.滑冰
B.乘坐电梯
C.猎豹奔跑
D.荡秋千
8.如图所示,四幅汽车标志设计中,下面通过平移得到的是( )
A.
B.
C.
D.
9.火车在铁轨上运动,车轮的运动是( )
A.旋转
B.平移
C.轴对称
D.既平移又旋转
10.将图案绕P点逆时针旋转90度,得到的图案是( )
A.
B.
C.
11.如图,长方形是按一定的比例放大或缩小,则x=( )
A.10
B.12
C.14
D.16
12.小华将一张正方形纸对折后剪去一个(如图),展开后是图( )
A.
B.
C.
D.
13.原图按2:1的比放大后的图形是( )
A.A
B.B
C.C
D.D
14.一个正方形的面积是100cm2,把它按10:1的比放大.放大后图形的面积是( )
A.1000cm2
B.2000cm2
C.10000cm2
15.上海在北京的南偏东30°方向,那么北京就在上海的( )方向。
A.东偏南30°
B.北偏西30°
C.北偏东30°
D.北偏西60°
16.如图,喷泉在苗圃的南偏西60°的位置上,那么苗圃在喷泉( )的位置上.
A.东偏北60°
B.南偏西60°
C.东偏北30°
D.南偏西30°
17.把一个直径5毫米的手表零件,画在图纸上直径是10厘米,这幅图纸的比例尺是( )
A.20:1
B.1:20
C.2:1
D.1:2
18.把改写成数值比例尺是( )
A.1:4000000
B.1:8000000
C.1:12000000
19.把一块三角形的地画在比例尺是1:500的图纸上,量得图上三角形的底是12厘米,高8厘米,这块地实际面积是( )
A.480平方米
B.240平方米
C.1200平方米
D.2400
平方米
二、填空题
1.如图,小明上午在理发店理发时,从镜子内看到背后普通时钟的时针与分针的位置如图所示,此时时间是
分.
2.三角形A绕点O按
时针方向旋转
度得到三角形B.
3.把一个长5cm、宽4cm的长方形按3:1放大,得到的图形的面积是
cm2.
4.一根3米长的绳子连续对折三次,每小段是全长的
,每小段长
米.
5.如图中小屋上的两点A,D的位置用数对表示是:A(
),D(
).
6.超市在电影院南偏西40°的方向上,距离电影院3千米,那么电影院在超市的
方向或
方向上,距离超市3千米.
7.如图,医院在学校
偏
度方向,距学校
千米处.
8.如图,小玲在小明的西偏北60°方向上,则小明在小玲的
偏
°方向上.
9.一幅地图的比例尺是1:3000000,这幅地图上两个城市之间的距离是20cm,那么这两个城市之间的实际距离是
km.
10.在一幅比例尺是1:500000的地图上量得郑州到开封的距离是15.6cm.郑州到开封的实际距离是
km.一辆汽车在9时15分从郑州出发,以每小时65km的速度行驶,预计
时
分可以到达开封.
11.看图填空.
某路公共汽车从机场到图书馆的行驶路线是:向
行驶
站到红星广场,再向
行驶
站到动物园,再向
行驶
站到图书馆.
三、应用题
1.一幅地图的比例尺是1:6000000,在这幅地图上量得A地到B地的距离是9.6cm。一辆汽车从A地开往B地,每时行80km,多少小时能到达?
2.在比例尺为1:50000000的地图上,量得甲乙两地的距离是8厘米,一架飞机从甲地飞往乙地用4小时,这架飞机平均每小时飞行多少千米?
3.荆州城,曾名为“江陵城”,“千里江陵一日还”说的就是荆州城.荆州城现存明清重建城墙东西长3.75千米,在比例尺是1:20000的地图上长度约是多少厘米?在这幅地图上量得城墙南北最宽相距6厘米,南北的实际距离是多少千米?
4.在比例尺为1:500000的地图上,量得A.B两地的图上距离是6cm,一辆汽车上午8时从A地以90千米/时的速度开往B地,到达B地的时间是几时?
四、操作题
1.(1)画出图形①的轴对称图形.
(2)画出把三角形AOB向下平移6个格后的三角形A′O′B′.
(3)画出三角形AOB绕B点逆时针旋转90°后的图形.
2.按要求画图(每个小方格边长表示1cm).
(1)把图A补全,使它成为一个轴对称图形.
(2)把图B先向右平移6格,再向上平移3格.
(3)把图C绕点O按顺时针方向旋转90°.
(4)画出图D按3:1的比放大后的图形.
3.按要求在方格纸中作图.
①根据给定的对称轴画出图形A的另一半.
②画出图形B向右平移4格后的图形.
③画出将图形C按2:1放大后的图形.
4.在方格纸上按要求画出图形.
(1)图形A向右平移5格得到图形B.
(2)图形B绕平移后的点O1,顺时针旋转90°,得到图形C.
(3)画出图形C关于直线L的对称图形D.
5.
6.按要求在如图的点子图中画图.
(1)三角形A绕点O逆时针旋转90°得到图形B.
(2)图形B向右平移5个单位得到图形C.
(3)请将三角形A按1:2缩小画在点子图上.
7.在图中完成下列问题.
(1)科技馆在学校北偏东30°方向200米处.请在图中标出科技馆的位置,并标出图上距离.
(2)南京路经过电影院,与上海路平行.请用直线标出南京路的位置.
8.小芳家要修一条小路到公路上,该怎样修最近?在图中画出来.
9.按要求做题.图中1个小方格的面积为1平方厘米.
(1)把三角形绕点B逆时针旋转90o,画出旋转后的图形.
(2)标出点D(2,2)和点E(6,2)的位置.
(3)以DE为下底,画一个上底为2厘米,高为3厘米的等腰梯形.
(4)画出的梯形的面积是
平方厘米.
答案
一、选择题
1.A。2.D。3.D.4.B.5.A.6.C.7.B.8.A.9.A.
10.B.11.B.12.A.13.C.14.C.15.B。16.C。
17.A。18.A.19.C.
二、填空题
1.10时45.
2.顺,90.
3.180.
4.;.
5.2,1;6,5.
6.北偏东40°方向;东偏北50°.
7.北,西30,6.
8.东,南,60.
9.600。
10.78,10,27.
11.东,1,东北,1,北,3.
三、应用题
1.解:9.6
=9.6×6000000
=57600000(厘米)
57600000厘米=576千米
576÷80=7.2(小时)
答:7.2小时到达。
2.解:8400000000(厘米)
400000000厘米=4000千米
4000÷4=1000(千米)
答:这架飞机平均每小时飞行1000千米。
3.解:3.75千米=375000厘米
37500018.75(厘米)
6120000(厘米)
120000厘米=1.2千米
答:在比例尺是1:20000的地图上长度约是18.75厘米,南北的实际距离是1.2千米.
4.解:63000000(厘米)
3000000厘米=30千米
30÷90(小时)=20(分钟)
8时+20分钟=8时20分
答:辆汽车上午8时从A地以90千米/时的速度开往B地,到达B地的时间是8时20分.
四、操作题
1.解:(1)画出图形①的轴对称图形(图形②).
(2)画出把三角形AOB向下平移6个格后的三角形A′O′B′.
(3)画出三角形AOB绕B点逆时针旋转90°后的图形(三角形A″O″B).
2.解:(1)把图A补全,使它成为一个轴对称图形(图中红色部分).
(2)把图B先向右平移6格,再向上平移3格(图中绿色部分).
(3)把图C绕点O按顺时针方向旋转90°(图中黄色部分).
(4)画出图D按3:1的比放大后的图形(图中蓝色部分).
3.解:①根据给定的对称轴画出图形A的另一半(图形A′).
②画出图形B向右平移4格后的图形图形B′).
③画出将图形C按2:1放大后的图形(图形C′).
4.解:(1)图形A向右平移5格得到图形B(图中红色部分).
(2)图形B绕平移后的点O1,顺时针旋转90°,得到图形C(图中绿色部分).
(3)画出图形C关于直线L的对称图形D(图中蓝色部分).
5.解:
6.解:(1)三角形A绕点O逆时针旋转90°得到图形B(下图红色部分).
(2)图形B向右平移5个单位得到图形C(下图绿色部分).
(3)请将三角形A按1:2缩小画在点子图上(图形D,下图蓝色部分).
7.解:(1)科技馆离学校实际距离200米,由比例尺1:10000得:
200米=20000厘米
20000÷10000=2(厘米)
所以科技馆到学校的图上距离是2厘米.
科技馆在学校北偏东30°方向200米处.(作图如下)
(2)南京路经过电影院,与上海路平行.用直线标出南京路的位置.(如图)
8.解:
9.解:(1)把三角形绕点B逆时针旋转90o,画出旋转后的图形(三角形A′BC′).
(2)标出点D(2,2)和点E(6,2)的位置(下图).
(3)以DE为下底,画一个上底为2厘米,高为3厘米的等腰梯形(等腰梯形DEFG).
(4)画出的梯形的面积是:
(2+4)×3
=6×3
=9(平方厘米).
故答案为:9.
