六年级数学下册 一课一练《总复习-图形与几何》习题4-北师大版(含答案)
文档属性
| 名称 | 六年级数学下册 一课一练《总复习-图形与几何》习题4-北师大版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 674.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 00:00:00 | ||
图片预览



文档简介
《总复习-图形与几何》习题4
一、选择题
1.把一张正方形纸按如下方法对折两次后,在如图所示的位置上打一个孔,把纸展开后得到的应是( )
A.
B.
C.
D.
2.下面的图形中,对称轴条数最多的是( )
A.正方形
B.等边三角形
C.长方形
D.圆形
3.下列图形中,是轴对称图形的是( )
A.三角形
B.平行四边形
C.梯形
D.圆
4.如图的图象绕虚线旋转一周,可以得到的几何体是( )
A.
B.
C.
D.
5.如图一个直角三角形ABC,如以AB边为轴旋转一周,得到的立体图形,计算它的体积正确的算式是( )
A.32×4π
B.42×3π
C.32×4π
D.42×3π
6.把一个长是5厘米,宽是2厘米的长方形按3:1放大在图纸上后,得到的图形的面积是( )平方厘米.
A.90
B.42
C.14
D.10
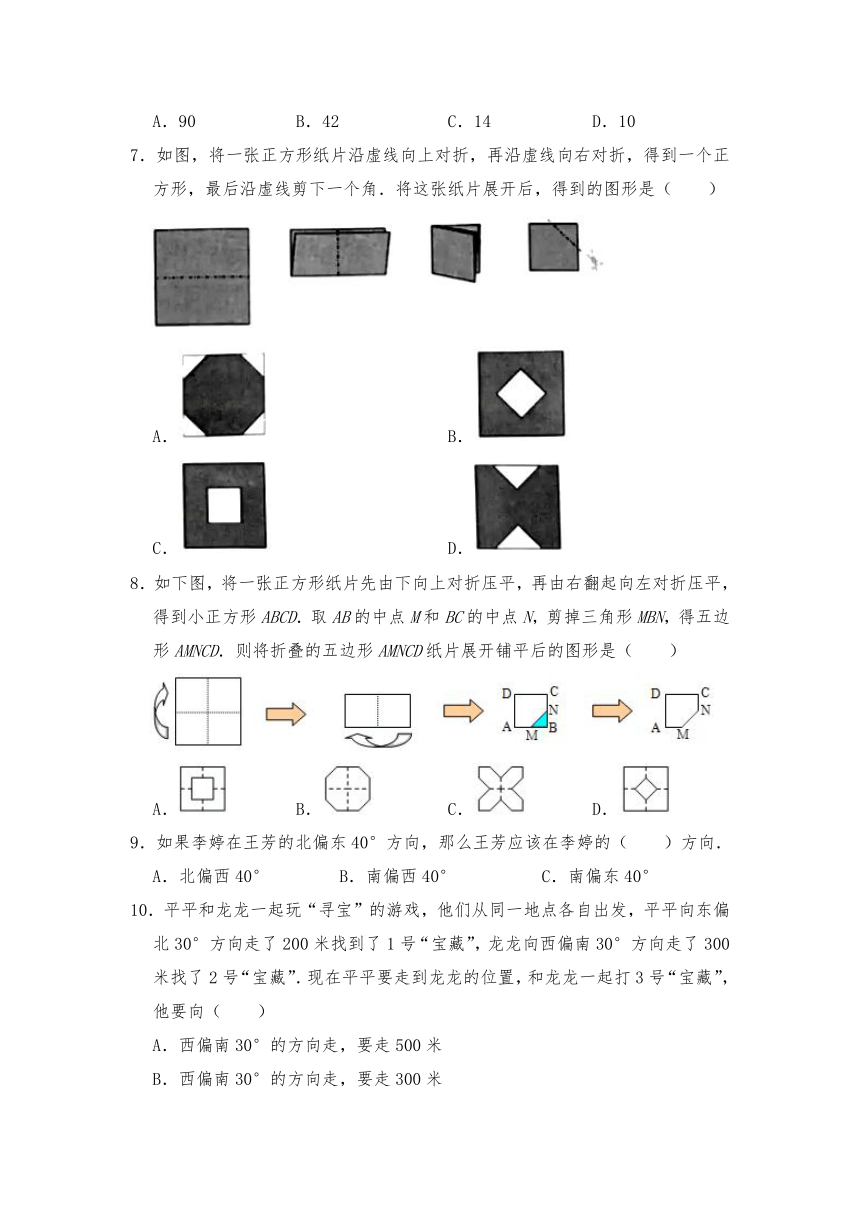
7.如图,将一张正方形纸片沿虚线向上对折,再沿虚线向右对折,得到一个正方形,最后沿虚线剪下一个角.将这张纸片展开后,得到的图形是( )
A.
B.
C.
D.
8.如下图,将一张正方形纸片先由下向上对折压平,再由右翻起向左对折压平,得到小正方形ABCD.取AB的中点M和BC的中点N,剪掉三角形MBN,得五边形AMNCD.则将折叠的五边形AMNCD纸片展开铺平后的图形是( )
A.
B.
C.
D.
9.如果李婷在王芳的北偏东40°方向,那么王芳应该在李婷的( )方向.
A.北偏西40°
B.南偏西40°
C.南偏东40°
10.平平和龙龙一起玩“寻宝”的游戏,他们从同一地点各自出发,平平向东偏北30°方向走了200米找到了1号“宝藏”,龙龙向西偏南30°方向走了300米找了2号“宝藏”.现在平平要走到龙龙的位置,和龙龙一起打3号“宝藏”,他要向( )
A.西偏南30°的方向走,要走500米
B.西偏南30°的方向走,要走300米
C.东偏北30°的方向走,要走500米
D.东偏北30°的方向走,要走300米
11.在平面图上,甲点和乙点(6,2)在同一行,与丙点(2,7)在同一列,甲点的位置用数对表示是( )
A.(2,2)
B.(7,6)
C.(6,7)
D.(2,6)
12.在中国象棋的棋盘上(如图),每枚棋子的行走路线都有自己的规则.如马走“日”,图中的“马”的位置在(6,3),它走一步,可以直接到达的位置有8个.那么,图中的“马”最少走( )步可以到达(7,2)呢?
A.1
B.2
C.3
D.4
13.小明座位的西南方向是张强的座位,那么小明在张强的( )方向.
A.东南
B.西北
C.东北
14.下列图形中对称轴最多的是( )
A.圆形
B.正方形
C.长方形
二、填空题
1.如图:把中间的长方形分别按一定比例缩小和放大得到了左右两个长方形.
(1)x=
cm,y=
cm
(2)根据得出的数据,写出一组比例
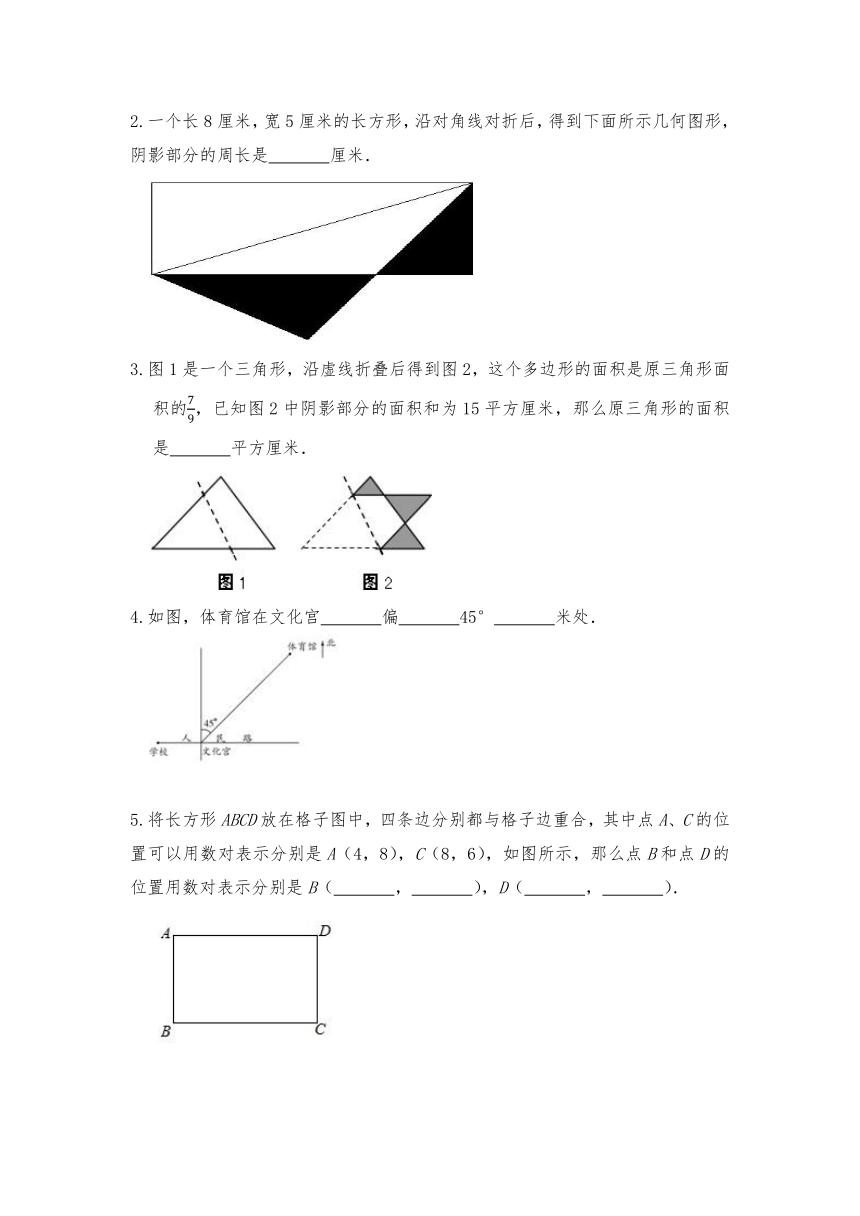
2.一个长8厘米,宽5厘米的长方形,沿对角线对折后,得到下面所示几何图形,阴影部分的周长是
厘米.
3.图1是一个三角形,沿虚线折叠后得到图2,这个多边形的面积是原三角形面积的,已知图2中阴影部分的面积和为15平方厘米,那么原三角形的面积是
平方厘米.
4.如图,体育馆在文化宫
偏
45°
米处.
5.将长方形ABCD放在格子图中,四条边分别都与格子边重合,其中点A、C的位置可以用数对表示分别是A(4,8),C(8,6),如图所示,那么点B和点D的位置用数对表示分别是B(
,
),D(
,
).
6.看图填空.某市中心广场四周建筑如图所示.
(1)医院距中心广场的图上距离是
cm,已知实际距离是200m,此图的比例尺是
.
(2)学校到图书馆的图上距离是
cm,实际距离是
m,如果淘气每分走50米,他从学校到图书馆需
分.
(3)笑笑从电影院出来后经中心广场到百货商店,实际走了
米.
7.四川广元昭化古城四面环山,三面临水,白龙江、嘉陵江在此交汇,形成了一个直径约5km的自然山水太极图.将此图画在比例尺是1:25000的地图上,直径是
cm,面积是
cm2.
8.在一幅比例尺是的地图上,量得两地距离是15厘米,这两地实际距离是
千米.
9.如右图,量一量福州与厦门两点间的图上距离是
厘米,这两个城市的实际距离是
千米.
10.小明面向正北方行走,走到十字路口处,转向右方继续行走,这时他面向的方向是
方。
三、判断题
1.由同一平面上的两个圆组成的图形一定是轴对称图形.(
)
2.一个长方形按2:1放大后,它的周长和面积都是原来的2倍.(
)
四、操作题
1.描点与画图.
(1)把平行四边形向下平移5格.
(2)图中点A的位置用数对表示是(
,
).把梯形绕点A逆时针旋转900,画出旋转后的图形.
(3)把三角形按3:1的比放大.
(4)画一个周长是16cm的长方形,长与宽的比是5:3.(图中每个小方格表示1cm2)
2.将图A绕“O”点按顺时针方向旋转90°后,得到图形B;再将图形B向右平移5格,得到图形C.在图中画出图形B与图形C.
3.(1)在方格图中画出一个三角形ABC,顶点分别是A(2,4),B(2,8),C(5,4).
(2)画出三角形ABC向右平移5格后的图形A′B′C′.
(3)画出三角形ABC绕点A顺时针旋转90°后的图形.
(4)按2:1画出三角形ABC放大后的图形.
4.量量、算算、画画.
下面三小丽以自己家为观测点,画出的一张平面图.
(1)汽车站在小丽家
方向
米处.
(2)商店在小丽家
偏
度方向
米处.
(3)学校在小丽家南偏西45°方向600米处,请标出学校的位置.
5.根据下面的描述画出路线图.(用1厘米的线段表示20米)
在金银岛西偏北45?距金银岛180米的地方停靠着一只小木船,小木船南偏东15?距小木船100米处是松树林,松树林的东偏北30?距松树林120米的位置是同学们的宿营地.
五、解答题
1.(1)图A是对称图形,请根据对称轴画出图形的另一半.
(2)画出图B先向右平移3格,再绕O点顺时针旋转90°后所得到的图形.
2.画出图形的另一半,使它成为一个轴对称图形.
3.在方格纸上按要求完成作业.
(1)将图A向左平移5格.
(2)将图B按点O顺时针方向旋转90°.
(3)以直线L为对称轴,画出已知图形C的轴对称图形.
4.画出三角形ABC绕B点顺时针旋转90°后的图形.
5.(1)按1:2的比画出三角形缩小后的图形.
(2)如果每个小方格的边长表示1厘米.缩小后三角形的面积是
平方厘米.
6.实践操作.
如图每个小正方形的边长表示1厘米.
(1)在正方形方格纸上有一个三角形ABC,用数对表示点C的位置是
.
(2)这个三角形的面积是
平方厘米.
(3)画出这个三角形绕C点顺时针旋转90°后得到的图形,再向右平移10格,只画出最终得到的图形.
(4)以点C(原图中的点C)为圆心画圆,所画圆的实际周长为188.4米,图上距离1厘米表示实际距离10米,在图中画出这个圆,并求出圆的图上面积.
7.甲地到乙地的实际距离是180千米,在一幅比例尺是1:6000000的地图上,应画多少厘米?
8.在一幅比例尺是1:2000000的地图上,量得甲、乙两个城市之间的高速公路的距离是5.5cm.在另一幅比例尺是1:5000000的地图上,这条公路的图上距离是多少厘米?
9.在比例尺1:6000000的地图上,量得甲乙两地的距离是8厘米,如果一辆汽车以每小时80千米的速度从甲地开出,几小时到达乙地?
10.①在图中标出你从A穿过机动车道的最短的线路
②求机动车道的实际宽度.
11.(1)三角形ABC
轴对称图形((填“是”或“不是”).
(2)如果图中点A表示为(1,1),点B表示为(4,1),那么点C表示为(
,
).
(3)三角形ABC绕点C逆时针旋转90°后,点A到达的位置A′点表示为(
,
).
(4)将三角形ABC按2:1放大,并画在方格纸上.放大后三角形的面积是
cm2.
12.图中每个小方格表示1平方厘米.
(1)把图中的三角形绕A点顺时针旋转90°,画出旋转后的图形.旋转后,B点的位置用数对表示是(
,
).
(2)按2:1的比画出三角形放大后的图形.放大后三角形的面积是
平方厘米.
答案
一、选择题
1.A。2.D.3.D.4.C。5.A.6.A。
7.A.8.D.9.B.10.A.11.A.12.B.13.C.14.A.
二、填空题
1.8;27;12:8=27:18.
2.26
3.27.
4.北、东、400.
5.4、6;8、8.
6.1.6,1:12500;5.5,687.5,13.75;375.
7.20、314.
8.900.
9.4.2,420.
10.东。
三、判断题
1.√.2.×.
四、操作题
1.解:(1)作图如下:
(2)A的位置用数对表示是(13,6).
作图如下:
(3)2×3=6(厘米),
作图如下:
(4)
作图如下:
16÷2=8(厘米),
5+3=8,
85(厘米),
83(厘米),
故答案为:13、6.
2.解:将图A绕“O”点按顺时针方向旋转90°后,得到图形B;再将图形B向右平移5格,得到图形C;如下图:
3.解:(1)三角形ABC三个顶点的位置分别是A(2,4),B(2,8),C(5,4)。作图如下:
(2)作图如下:
(3)作图如下:
(4)作图如下:
4.解:根据平面图中条件可得:
(1)200×4=800(米),
答:汽车站在小丽家正东方向800米处.
故答案为:正东;800.
(2)200×2=400(米),
答:商店在小丽家北偏西30°方向400米处.
故答案为:北;西30;400.
(3)在图中画出南偏西45°方向,根据题意可画出学校的位置如图所示.
5.解:因为图上距离1厘米表示实际距离20米,
则180÷20=9(厘米)
100÷20=5(厘米)
120÷20=6(厘米)
再据各个地点与金银岛的方向关系及小木船与松树林的方向关系,
画出方位图如下:
五、解答题
1.解:画图如下:
2.解:作图如下:
3.解:(1)将图A向左平移5格(下图).
(2)将图B按点O顺时针方向旋转90°(下图).
(3)以直线L为对称轴,画出已知图形C的轴对称图形(下图).
4.解:根据题干分析画图如下:
5.解:(1)4÷2=2(厘米)
6÷2=3(厘米)
作图如下:
(2)2×3÷2=3(平方厘米)
答:缩小后三角形的面积是3平方厘米.
故答案为:3.
6.解:(1)在正方形方格纸上有一个三角形ABC,用数对表示点C的位置是(3,4).
(2)2×3÷2=3(平方厘米)
答:这个三角形的面积是3平方厘米.
(3)画图如下:
(4)188.4÷3.14÷2=30(米)
30÷10=3(厘米)
3.14×3×3=28.26(平方厘米)
答:圆的图上面积是28.26平方厘米.
故答案为:(3,4);3,28.26平方厘米.
7.解:180千米=18000000厘米,
180000003(厘米);
答:应画3厘米.
8.解:5.5,
=11000000,
=2.2(厘米);
答:在另一幅比例尺是1:5000000的地图上,这条公路的图上距离是2.2厘米.
9.解:甲、乙两地的距离:
848000000(厘米)=480(千米)
从甲地开往乙地,需要:
480÷80=6(小时)
答:从甲地开往乙地,需要6小时.
10.解:(1)如图,
(2)量得机动车道的图上距离为1.5厘米,
解设机动车道的实际宽度为x厘米,根据题意得
1.5:x=1:1000,
x=1.5×1000,
x=1500
1500厘米=15米.
答:机动车道的实际宽度为15米.
11.解:(1)三角形ABC是轴对称图形.
(2)如果图中点A表示为(1,1),点B表示为(4,1),那么点C表示为(4,4).
(3)三角形ABC绕点C逆时针旋转90°后,点A到达的位置A′点表示为(7,1).
(4)放大后的底和高是:
3×2=6(厘米)
6×6÷2=18(平方厘米)
答:放大后三角形的面积是18平方厘米.
作图如下:
故答案为:是;4,4;7,1;18.
12.解:(1)作图如下:旋转后,B点的位置用数对表示是5,4;
(2)6×4÷2=12(平方厘米);
答:旋转后,B点的位置用数对表示是5,4;放大后三角形的面积是12平方厘米.
故答案为:5,4;12.
一、选择题
1.把一张正方形纸按如下方法对折两次后,在如图所示的位置上打一个孔,把纸展开后得到的应是( )
A.
B.
C.
D.
2.下面的图形中,对称轴条数最多的是( )
A.正方形
B.等边三角形
C.长方形
D.圆形
3.下列图形中,是轴对称图形的是( )
A.三角形
B.平行四边形
C.梯形
D.圆
4.如图的图象绕虚线旋转一周,可以得到的几何体是( )
A.
B.
C.
D.
5.如图一个直角三角形ABC,如以AB边为轴旋转一周,得到的立体图形,计算它的体积正确的算式是( )
A.32×4π
B.42×3π
C.32×4π
D.42×3π
6.把一个长是5厘米,宽是2厘米的长方形按3:1放大在图纸上后,得到的图形的面积是( )平方厘米.
A.90
B.42
C.14
D.10
7.如图,将一张正方形纸片沿虚线向上对折,再沿虚线向右对折,得到一个正方形,最后沿虚线剪下一个角.将这张纸片展开后,得到的图形是( )
A.
B.
C.
D.
8.如下图,将一张正方形纸片先由下向上对折压平,再由右翻起向左对折压平,得到小正方形ABCD.取AB的中点M和BC的中点N,剪掉三角形MBN,得五边形AMNCD.则将折叠的五边形AMNCD纸片展开铺平后的图形是( )
A.
B.
C.
D.
9.如果李婷在王芳的北偏东40°方向,那么王芳应该在李婷的( )方向.
A.北偏西40°
B.南偏西40°
C.南偏东40°
10.平平和龙龙一起玩“寻宝”的游戏,他们从同一地点各自出发,平平向东偏北30°方向走了200米找到了1号“宝藏”,龙龙向西偏南30°方向走了300米找了2号“宝藏”.现在平平要走到龙龙的位置,和龙龙一起打3号“宝藏”,他要向( )
A.西偏南30°的方向走,要走500米
B.西偏南30°的方向走,要走300米
C.东偏北30°的方向走,要走500米
D.东偏北30°的方向走,要走300米
11.在平面图上,甲点和乙点(6,2)在同一行,与丙点(2,7)在同一列,甲点的位置用数对表示是( )
A.(2,2)
B.(7,6)
C.(6,7)
D.(2,6)
12.在中国象棋的棋盘上(如图),每枚棋子的行走路线都有自己的规则.如马走“日”,图中的“马”的位置在(6,3),它走一步,可以直接到达的位置有8个.那么,图中的“马”最少走( )步可以到达(7,2)呢?
A.1
B.2
C.3
D.4
13.小明座位的西南方向是张强的座位,那么小明在张强的( )方向.
A.东南
B.西北
C.东北
14.下列图形中对称轴最多的是( )
A.圆形
B.正方形
C.长方形
二、填空题
1.如图:把中间的长方形分别按一定比例缩小和放大得到了左右两个长方形.
(1)x=
cm,y=
cm
(2)根据得出的数据,写出一组比例
2.一个长8厘米,宽5厘米的长方形,沿对角线对折后,得到下面所示几何图形,阴影部分的周长是
厘米.
3.图1是一个三角形,沿虚线折叠后得到图2,这个多边形的面积是原三角形面积的,已知图2中阴影部分的面积和为15平方厘米,那么原三角形的面积是
平方厘米.
4.如图,体育馆在文化宫
偏
45°
米处.
5.将长方形ABCD放在格子图中,四条边分别都与格子边重合,其中点A、C的位置可以用数对表示分别是A(4,8),C(8,6),如图所示,那么点B和点D的位置用数对表示分别是B(
,
),D(
,
).
6.看图填空.某市中心广场四周建筑如图所示.
(1)医院距中心广场的图上距离是
cm,已知实际距离是200m,此图的比例尺是
.
(2)学校到图书馆的图上距离是
cm,实际距离是
m,如果淘气每分走50米,他从学校到图书馆需
分.
(3)笑笑从电影院出来后经中心广场到百货商店,实际走了
米.
7.四川广元昭化古城四面环山,三面临水,白龙江、嘉陵江在此交汇,形成了一个直径约5km的自然山水太极图.将此图画在比例尺是1:25000的地图上,直径是
cm,面积是
cm2.
8.在一幅比例尺是的地图上,量得两地距离是15厘米,这两地实际距离是
千米.
9.如右图,量一量福州与厦门两点间的图上距离是
厘米,这两个城市的实际距离是
千米.
10.小明面向正北方行走,走到十字路口处,转向右方继续行走,这时他面向的方向是
方。
三、判断题
1.由同一平面上的两个圆组成的图形一定是轴对称图形.(
)
2.一个长方形按2:1放大后,它的周长和面积都是原来的2倍.(
)
四、操作题
1.描点与画图.
(1)把平行四边形向下平移5格.
(2)图中点A的位置用数对表示是(
,
).把梯形绕点A逆时针旋转900,画出旋转后的图形.
(3)把三角形按3:1的比放大.
(4)画一个周长是16cm的长方形,长与宽的比是5:3.(图中每个小方格表示1cm2)
2.将图A绕“O”点按顺时针方向旋转90°后,得到图形B;再将图形B向右平移5格,得到图形C.在图中画出图形B与图形C.
3.(1)在方格图中画出一个三角形ABC,顶点分别是A(2,4),B(2,8),C(5,4).
(2)画出三角形ABC向右平移5格后的图形A′B′C′.
(3)画出三角形ABC绕点A顺时针旋转90°后的图形.
(4)按2:1画出三角形ABC放大后的图形.
4.量量、算算、画画.
下面三小丽以自己家为观测点,画出的一张平面图.
(1)汽车站在小丽家
方向
米处.
(2)商店在小丽家
偏
度方向
米处.
(3)学校在小丽家南偏西45°方向600米处,请标出学校的位置.
5.根据下面的描述画出路线图.(用1厘米的线段表示20米)
在金银岛西偏北45?距金银岛180米的地方停靠着一只小木船,小木船南偏东15?距小木船100米处是松树林,松树林的东偏北30?距松树林120米的位置是同学们的宿营地.
五、解答题
1.(1)图A是对称图形,请根据对称轴画出图形的另一半.
(2)画出图B先向右平移3格,再绕O点顺时针旋转90°后所得到的图形.
2.画出图形的另一半,使它成为一个轴对称图形.
3.在方格纸上按要求完成作业.
(1)将图A向左平移5格.
(2)将图B按点O顺时针方向旋转90°.
(3)以直线L为对称轴,画出已知图形C的轴对称图形.
4.画出三角形ABC绕B点顺时针旋转90°后的图形.
5.(1)按1:2的比画出三角形缩小后的图形.
(2)如果每个小方格的边长表示1厘米.缩小后三角形的面积是
平方厘米.
6.实践操作.
如图每个小正方形的边长表示1厘米.
(1)在正方形方格纸上有一个三角形ABC,用数对表示点C的位置是
.
(2)这个三角形的面积是
平方厘米.
(3)画出这个三角形绕C点顺时针旋转90°后得到的图形,再向右平移10格,只画出最终得到的图形.
(4)以点C(原图中的点C)为圆心画圆,所画圆的实际周长为188.4米,图上距离1厘米表示实际距离10米,在图中画出这个圆,并求出圆的图上面积.
7.甲地到乙地的实际距离是180千米,在一幅比例尺是1:6000000的地图上,应画多少厘米?
8.在一幅比例尺是1:2000000的地图上,量得甲、乙两个城市之间的高速公路的距离是5.5cm.在另一幅比例尺是1:5000000的地图上,这条公路的图上距离是多少厘米?
9.在比例尺1:6000000的地图上,量得甲乙两地的距离是8厘米,如果一辆汽车以每小时80千米的速度从甲地开出,几小时到达乙地?
10.①在图中标出你从A穿过机动车道的最短的线路
②求机动车道的实际宽度.
11.(1)三角形ABC
轴对称图形((填“是”或“不是”).
(2)如果图中点A表示为(1,1),点B表示为(4,1),那么点C表示为(
,
).
(3)三角形ABC绕点C逆时针旋转90°后,点A到达的位置A′点表示为(
,
).
(4)将三角形ABC按2:1放大,并画在方格纸上.放大后三角形的面积是
cm2.
12.图中每个小方格表示1平方厘米.
(1)把图中的三角形绕A点顺时针旋转90°,画出旋转后的图形.旋转后,B点的位置用数对表示是(
,
).
(2)按2:1的比画出三角形放大后的图形.放大后三角形的面积是
平方厘米.
答案
一、选择题
1.A。2.D.3.D.4.C。5.A.6.A。
7.A.8.D.9.B.10.A.11.A.12.B.13.C.14.A.
二、填空题
1.8;27;12:8=27:18.
2.26
3.27.
4.北、东、400.
5.4、6;8、8.
6.1.6,1:12500;5.5,687.5,13.75;375.
7.20、314.
8.900.
9.4.2,420.
10.东。
三、判断题
1.√.2.×.
四、操作题
1.解:(1)作图如下:
(2)A的位置用数对表示是(13,6).
作图如下:
(3)2×3=6(厘米),
作图如下:
(4)
作图如下:
16÷2=8(厘米),
5+3=8,
85(厘米),
83(厘米),
故答案为:13、6.
2.解:将图A绕“O”点按顺时针方向旋转90°后,得到图形B;再将图形B向右平移5格,得到图形C;如下图:
3.解:(1)三角形ABC三个顶点的位置分别是A(2,4),B(2,8),C(5,4)。作图如下:
(2)作图如下:
(3)作图如下:
(4)作图如下:
4.解:根据平面图中条件可得:
(1)200×4=800(米),
答:汽车站在小丽家正东方向800米处.
故答案为:正东;800.
(2)200×2=400(米),
答:商店在小丽家北偏西30°方向400米处.
故答案为:北;西30;400.
(3)在图中画出南偏西45°方向,根据题意可画出学校的位置如图所示.
5.解:因为图上距离1厘米表示实际距离20米,
则180÷20=9(厘米)
100÷20=5(厘米)
120÷20=6(厘米)
再据各个地点与金银岛的方向关系及小木船与松树林的方向关系,
画出方位图如下:
五、解答题
1.解:画图如下:
2.解:作图如下:
3.解:(1)将图A向左平移5格(下图).
(2)将图B按点O顺时针方向旋转90°(下图).
(3)以直线L为对称轴,画出已知图形C的轴对称图形(下图).
4.解:根据题干分析画图如下:
5.解:(1)4÷2=2(厘米)
6÷2=3(厘米)
作图如下:
(2)2×3÷2=3(平方厘米)
答:缩小后三角形的面积是3平方厘米.
故答案为:3.
6.解:(1)在正方形方格纸上有一个三角形ABC,用数对表示点C的位置是(3,4).
(2)2×3÷2=3(平方厘米)
答:这个三角形的面积是3平方厘米.
(3)画图如下:
(4)188.4÷3.14÷2=30(米)
30÷10=3(厘米)
3.14×3×3=28.26(平方厘米)
答:圆的图上面积是28.26平方厘米.
故答案为:(3,4);3,28.26平方厘米.
7.解:180千米=18000000厘米,
180000003(厘米);
答:应画3厘米.
8.解:5.5,
=11000000,
=2.2(厘米);
答:在另一幅比例尺是1:5000000的地图上,这条公路的图上距离是2.2厘米.
9.解:甲、乙两地的距离:
848000000(厘米)=480(千米)
从甲地开往乙地,需要:
480÷80=6(小时)
答:从甲地开往乙地,需要6小时.
10.解:(1)如图,
(2)量得机动车道的图上距离为1.5厘米,
解设机动车道的实际宽度为x厘米,根据题意得
1.5:x=1:1000,
x=1.5×1000,
x=1500
1500厘米=15米.
答:机动车道的实际宽度为15米.
11.解:(1)三角形ABC是轴对称图形.
(2)如果图中点A表示为(1,1),点B表示为(4,1),那么点C表示为(4,4).
(3)三角形ABC绕点C逆时针旋转90°后,点A到达的位置A′点表示为(7,1).
(4)放大后的底和高是:
3×2=6(厘米)
6×6÷2=18(平方厘米)
答:放大后三角形的面积是18平方厘米.
作图如下:
故答案为:是;4,4;7,1;18.
12.解:(1)作图如下:旋转后,B点的位置用数对表示是5,4;
(2)6×4÷2=12(平方厘米);
答:旋转后,B点的位置用数对表示是5,4;放大后三角形的面积是12平方厘米.
故答案为:5,4;12.
