沪科版 初中数学九年级上册第22章 相似三角形复习课课件(15张)
文档属性
| 名称 | 沪科版 初中数学九年级上册第22章 相似三角形复习课课件(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 338.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 09:04:11 | ||
图片预览



文档简介
(共15张PPT)
相似三角形
复习课
一、复习:
1、相似三角形的定义是什么?
答:
对应角
相等,
对应边
成比例
的两个三角形叫做相似三角形.
2、判定两个三角形相似有哪些方法?
答:
A、用定义;
B、用预备定理;
C、用判定定理1、2、3.
D、直角三角形相似的判定定理
一.填空选择题:
1.(1)
△
ABC中,D、E分别是AB、AC上的点,且∠AED=
∠
B,那么△
AED
∽
△
ABC,从而
(2)
△
ABC中,AB的中点为E,AC的中点为D,连结ED,
则△
AED与△
ABC的相似比为______.
2.如图,DE∥BC,
AD:DB=2:3,
则△
AED和△
ABC
的相似比为___.
3.
已知三角形甲各边的比为3:4:6,
和它相似的三角形乙
的最大边为10cm,
则三角形乙的最短边为______cm.
4.等腰三角形ABC的腰长为18cm,底边长为6cm,在腰AC上取点D,
使△ABC∽
△BDC,
则DC=______.
AC
2:5
5
2cm
1:2
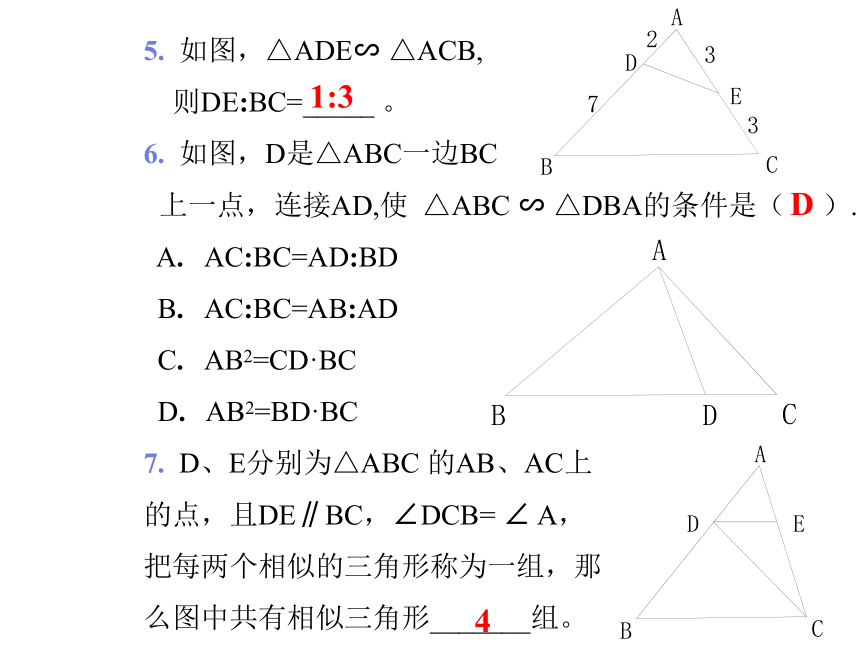
5.
如图,△ADE∽
△ACB,
则DE:BC=_____
。
6.
如图,D是△ABC一边BC
上一点,连接AD,使
△ABC
∽
△DBA的条件是(
).
A.
AC:BC=AD:BD
B.
AC:BC=AB:AD
C.
AB2=CD·BC
D.
AB2=BD·BC
7.
D、E分别为△ABC
的AB、AC上
的点,且DE∥BC,∠DCB=
∠
A,
把每两个相似的三角形称为一组,那
么图中共有相似三角形_______组。
1:3
D
4
二、证明题:
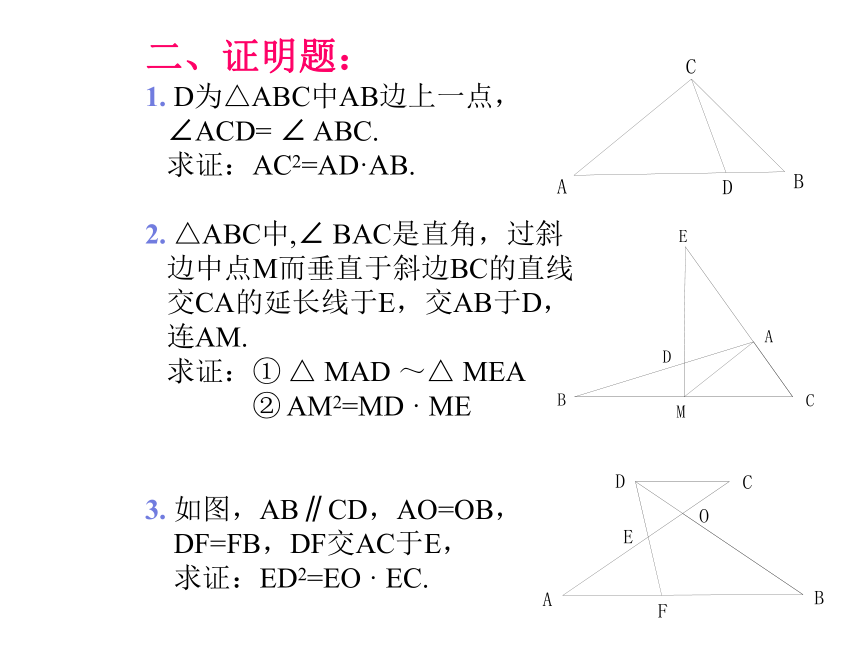
1.
D为△ABC中AB边上一点,
∠ACD=
∠
ABC.
求证:AC2=AD·AB.
2.
△ABC中,∠
BAC是直角,过斜
边中点M而垂直于斜边BC的直线
交CA的延长线于E,交AB于D,
连AM.
求证:①
△
MAD
~△
MEA
②
AM2=MD
·
ME
3.
如图,AB∥CD,AO=OB,
DF=FB,DF交AC于E,
求证:ED2=EO
·
EC.
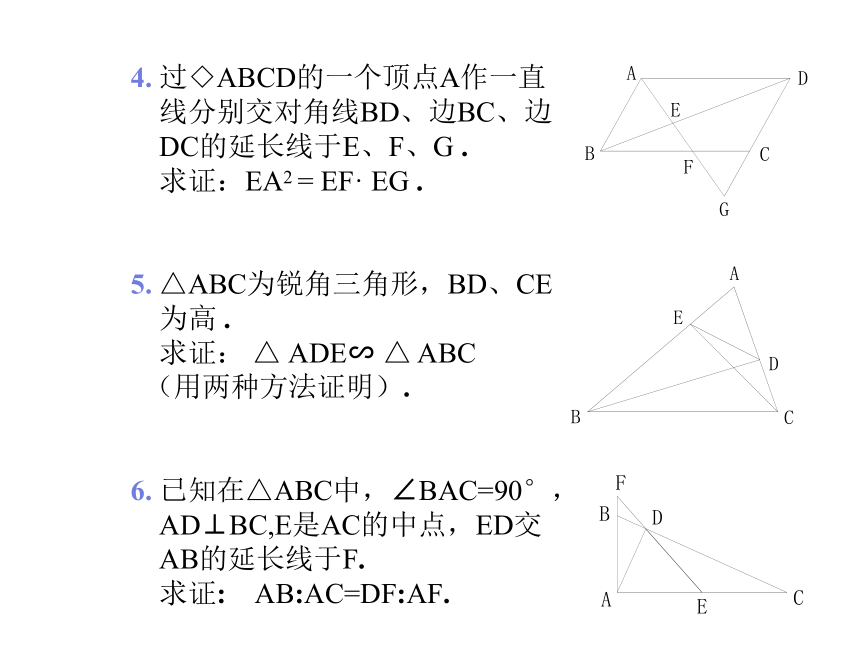
4.
过◇ABCD的一个顶点A作一直
线分别交对角线BD、边BC、边
DC的延长线于E、F、G
.
求证:EA2
=
EF·
EG
.
5.
△ABC为锐角三角形,BD、CE
为高
.
求证:
△
ADE∽
△
ABC
(用两种方法证明).
6.
已知在△ABC中,∠BAC=90°,
AD⊥BC,E是AC的中点,ED交
AB的延长线于F.
求证:
AB:AC=DF:AF.
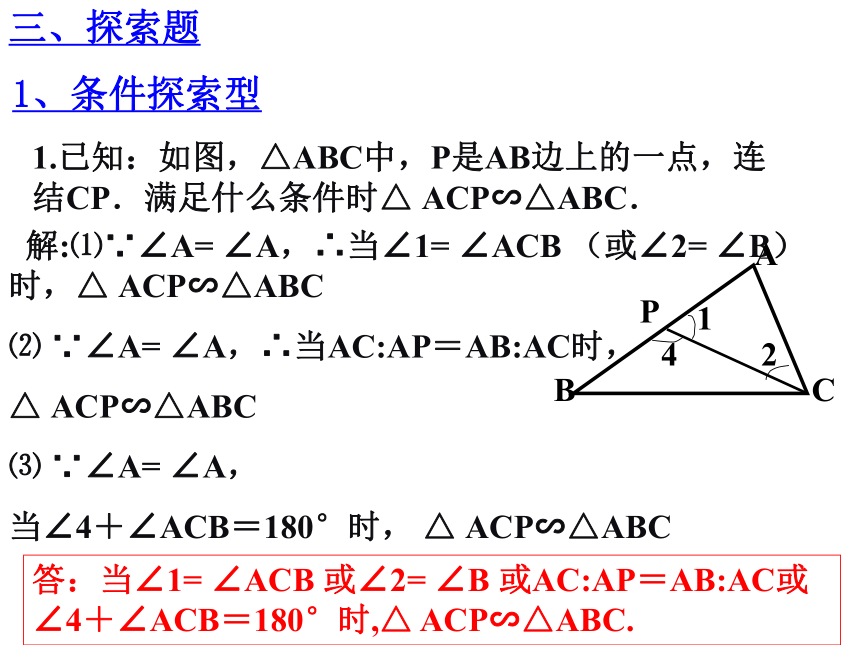
1.已知:如图,△ABC中,P是AB边上的一点,连结CP.满足什么条件时△
ACP∽△ABC.
解:⑴∵∠A=
∠A,∴当∠1=
∠ACB
(或∠2=
∠B)时,△
ACP∽△ABC
⑵
∵∠A=
∠A,∴当AC:AP=AB:AC时,
△
ACP∽△ABC
⑶
∵∠A=
∠A,
当∠4+∠ACB=180°时,
△
ACP∽△ABC
答:当∠1=
∠ACB
或∠2=
∠B
或AC:AP=AB:AC或∠4+∠ACB=180°时,△
ACP∽△ABC.
A
P
B
C
1
2
4
1、条件探索型
三、探索题
2.如图:已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b之间满足怎样的关系式时,两三角形相似
D
A
B
C
a
b
解:⑴∵
∠1=∠D=90°
∴当
时,即当
时,
△ABC∽
△CDB,∴
⑵∵
∠1=∠D=90°
∴当
时,即当
时,
△ABC∽
△BDC,
∴
答:略.
1
这类题型结论是明确的,而需要完备使结论成立的条件. 解题思路是:从给定结论出发,通过逆向思考寻求使结论成立的条件.
1.将两块完全相同的等腰直角三角板摆成如图的样子,假设图形中的所有点、线都在同一平面内,则图中有相似(不包括全等)三角形吗?如有,把它们一
一写出来.
C
解:有相似三角形,它们是:△ADE∽
△BAE,
△BAE
∽
△CDA
,△ADE∽
△CDA(
△ADE∽
△BAE
∽
△CDA)
2、结论探索型
A
B
D
E
G
F
1
2
2.△在ABC中,AB>AC,过AB上一点D作直线DE交另一边于E,使所得三角形与原三角形相似,画出满足条件的图形.
E
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
E
E
E
这类题型的特征是有条件而无结论,要确定这些条件下可能出现的结论. 解题思路是:从所给条件出发,通过分析、比较、猜想、寻求多种解法和结论,再进行证明.
3、存在探索型
如图,
DE是△ABC的中位线,在射线AF上是否存在点M,使△MEC与△ADE相似,若存在,请先确定点
M,再证明这两个三角形相似,若不存在,请说明理由.
A
D
B
C
E
F
证明:连结MC, ∵DE是△ABC的中位线, ∴DE∥BC,AE=EC, 又∵ME⊥AC,
∴AM=CM, ∴
∠1=
∠2
, ∵∠B=90°, ∴
∠4=
∠B=
90°,
∵AF
∥BC,AM
∥DE,
∴
∠1=
∠2
, ∴
∠3=
∠2
, ∵
∠ADE=
∠MEC=90
°
,
∴
△ADE
∽△MEC.
A
D
B
C
E
F
1
2
3
M
解:存在.过点E作AC的垂线,与AF交于一点,即M点(或作∠MCA=
∠AED).
4
所谓存在性问题,一般是要求确定满足某些特定要求的元素有或没有的问题. 解题思路是:先假定所需探索的对象存在或结论成立,以此为依据进行计算或推理,若由此推出矛盾,则假定是错误的,从而给出否定的结论,否则给出肯定的证明.
小
结
相
似
三
角
形
2.定义
3.性质
4.判定
5.应用
1.线段成比例
1.比例的基本性质
2.合比性质
3.等比性质
4.平行线分线段成比例定理及推论
1.AA
2.SAS
3.SSS
4.HL
对应高,中线,角平分线的比等于相似比
对应周长的比等于相似比
面积比等于相似比的平方
相似三角形
复习课
一、复习:
1、相似三角形的定义是什么?
答:
对应角
相等,
对应边
成比例
的两个三角形叫做相似三角形.
2、判定两个三角形相似有哪些方法?
答:
A、用定义;
B、用预备定理;
C、用判定定理1、2、3.
D、直角三角形相似的判定定理
一.填空选择题:
1.(1)
△
ABC中,D、E分别是AB、AC上的点,且∠AED=
∠
B,那么△
AED
∽
△
ABC,从而
(2)
△
ABC中,AB的中点为E,AC的中点为D,连结ED,
则△
AED与△
ABC的相似比为______.
2.如图,DE∥BC,
AD:DB=2:3,
则△
AED和△
ABC
的相似比为___.
3.
已知三角形甲各边的比为3:4:6,
和它相似的三角形乙
的最大边为10cm,
则三角形乙的最短边为______cm.
4.等腰三角形ABC的腰长为18cm,底边长为6cm,在腰AC上取点D,
使△ABC∽
△BDC,
则DC=______.
AC
2:5
5
2cm
1:2
5.
如图,△ADE∽
△ACB,
则DE:BC=_____
。
6.
如图,D是△ABC一边BC
上一点,连接AD,使
△ABC
∽
△DBA的条件是(
).
A.
AC:BC=AD:BD
B.
AC:BC=AB:AD
C.
AB2=CD·BC
D.
AB2=BD·BC
7.
D、E分别为△ABC
的AB、AC上
的点,且DE∥BC,∠DCB=
∠
A,
把每两个相似的三角形称为一组,那
么图中共有相似三角形_______组。
1:3
D
4
二、证明题:
1.
D为△ABC中AB边上一点,
∠ACD=
∠
ABC.
求证:AC2=AD·AB.
2.
△ABC中,∠
BAC是直角,过斜
边中点M而垂直于斜边BC的直线
交CA的延长线于E,交AB于D,
连AM.
求证:①
△
MAD
~△
MEA
②
AM2=MD
·
ME
3.
如图,AB∥CD,AO=OB,
DF=FB,DF交AC于E,
求证:ED2=EO
·
EC.
4.
过◇ABCD的一个顶点A作一直
线分别交对角线BD、边BC、边
DC的延长线于E、F、G
.
求证:EA2
=
EF·
EG
.
5.
△ABC为锐角三角形,BD、CE
为高
.
求证:
△
ADE∽
△
ABC
(用两种方法证明).
6.
已知在△ABC中,∠BAC=90°,
AD⊥BC,E是AC的中点,ED交
AB的延长线于F.
求证:
AB:AC=DF:AF.
1.已知:如图,△ABC中,P是AB边上的一点,连结CP.满足什么条件时△
ACP∽△ABC.
解:⑴∵∠A=
∠A,∴当∠1=
∠ACB
(或∠2=
∠B)时,△
ACP∽△ABC
⑵
∵∠A=
∠A,∴当AC:AP=AB:AC时,
△
ACP∽△ABC
⑶
∵∠A=
∠A,
当∠4+∠ACB=180°时,
△
ACP∽△ABC
答:当∠1=
∠ACB
或∠2=
∠B
或AC:AP=AB:AC或∠4+∠ACB=180°时,△
ACP∽△ABC.
A
P
B
C
1
2
4
1、条件探索型
三、探索题
2.如图:已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a、b之间满足怎样的关系式时,两三角形相似
D
A
B
C
a
b
解:⑴∵
∠1=∠D=90°
∴当
时,即当
时,
△ABC∽
△CDB,∴
⑵∵
∠1=∠D=90°
∴当
时,即当
时,
△ABC∽
△BDC,
∴
答:略.
1
这类题型结论是明确的,而需要完备使结论成立的条件. 解题思路是:从给定结论出发,通过逆向思考寻求使结论成立的条件.
1.将两块完全相同的等腰直角三角板摆成如图的样子,假设图形中的所有点、线都在同一平面内,则图中有相似(不包括全等)三角形吗?如有,把它们一
一写出来.
C
解:有相似三角形,它们是:△ADE∽
△BAE,
△BAE
∽
△CDA
,△ADE∽
△CDA(
△ADE∽
△BAE
∽
△CDA)
2、结论探索型
A
B
D
E
G
F
1
2
2.△在ABC中,AB>AC,过AB上一点D作直线DE交另一边于E,使所得三角形与原三角形相似,画出满足条件的图形.
E
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
E
E
E
这类题型的特征是有条件而无结论,要确定这些条件下可能出现的结论. 解题思路是:从所给条件出发,通过分析、比较、猜想、寻求多种解法和结论,再进行证明.
3、存在探索型
如图,
DE是△ABC的中位线,在射线AF上是否存在点M,使△MEC与△ADE相似,若存在,请先确定点
M,再证明这两个三角形相似,若不存在,请说明理由.
A
D
B
C
E
F
证明:连结MC, ∵DE是△ABC的中位线, ∴DE∥BC,AE=EC, 又∵ME⊥AC,
∴AM=CM, ∴
∠1=
∠2
, ∵∠B=90°, ∴
∠4=
∠B=
90°,
∵AF
∥BC,AM
∥DE,
∴
∠1=
∠2
, ∴
∠3=
∠2
, ∵
∠ADE=
∠MEC=90
°
,
∴
△ADE
∽△MEC.
A
D
B
C
E
F
1
2
3
M
解:存在.过点E作AC的垂线,与AF交于一点,即M点(或作∠MCA=
∠AED).
4
所谓存在性问题,一般是要求确定满足某些特定要求的元素有或没有的问题. 解题思路是:先假定所需探索的对象存在或结论成立,以此为依据进行计算或推理,若由此推出矛盾,则假定是错误的,从而给出否定的结论,否则给出肯定的证明.
小
结
相
似
三
角
形
2.定义
3.性质
4.判定
5.应用
1.线段成比例
1.比例的基本性质
2.合比性质
3.等比性质
4.平行线分线段成比例定理及推论
1.AA
2.SAS
3.SSS
4.HL
对应高,中线,角平分线的比等于相似比
对应周长的比等于相似比
面积比等于相似比的平方
