2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题(word解析版)
文档属性
| 名称 | 2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 168.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 16:43:14 | ||
图片预览


文档简介
2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题
一.选择题(共12小题,满分48分,每小题4分)
1.下列计算正确的是( )
A.(﹣3ab2)2=6a2b4
B.﹣6a3b÷3ab=﹣2a2b
C.(a2)3﹣(﹣a3)2=0
D.(a+1)2=a2+1
2.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90°
B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180°
D.∠α+∠β+∠γ=180°
3.下列计算中,正确的是( )
A.5a3?3a2=15a6
B.2x2?5x2=10x4
C.3x2?2x2=6x2
D.5y3?3y5=15y15
4.如图,已知直线上顺次三个点A、B、C,已知AB=10cm,BC=4cm.D是AC的中点,M是AB的中点,那么MD=( )cm
A.4
B.3
C.2
D.1
5.下列计算正确的是( )
A.(a﹣b)(﹣a﹣b)=a2﹣b2
B.2a3+3a3=5a6
C.6x3y2÷3x=2x2y2
D.(﹣2x2)3=﹣6x6
6.为了了解我县初一4300名学生在疫情期间“数学空课”的学习情况,全县组织了一次数学检测,从中抽取100名考生的成绩进行统计分析,以下说法正确的是( )
A.这100名考生是总体的一个样本
B.4300名考生是总体
C.每位学生的数学成绩是个体
D.100名学生是样本容量
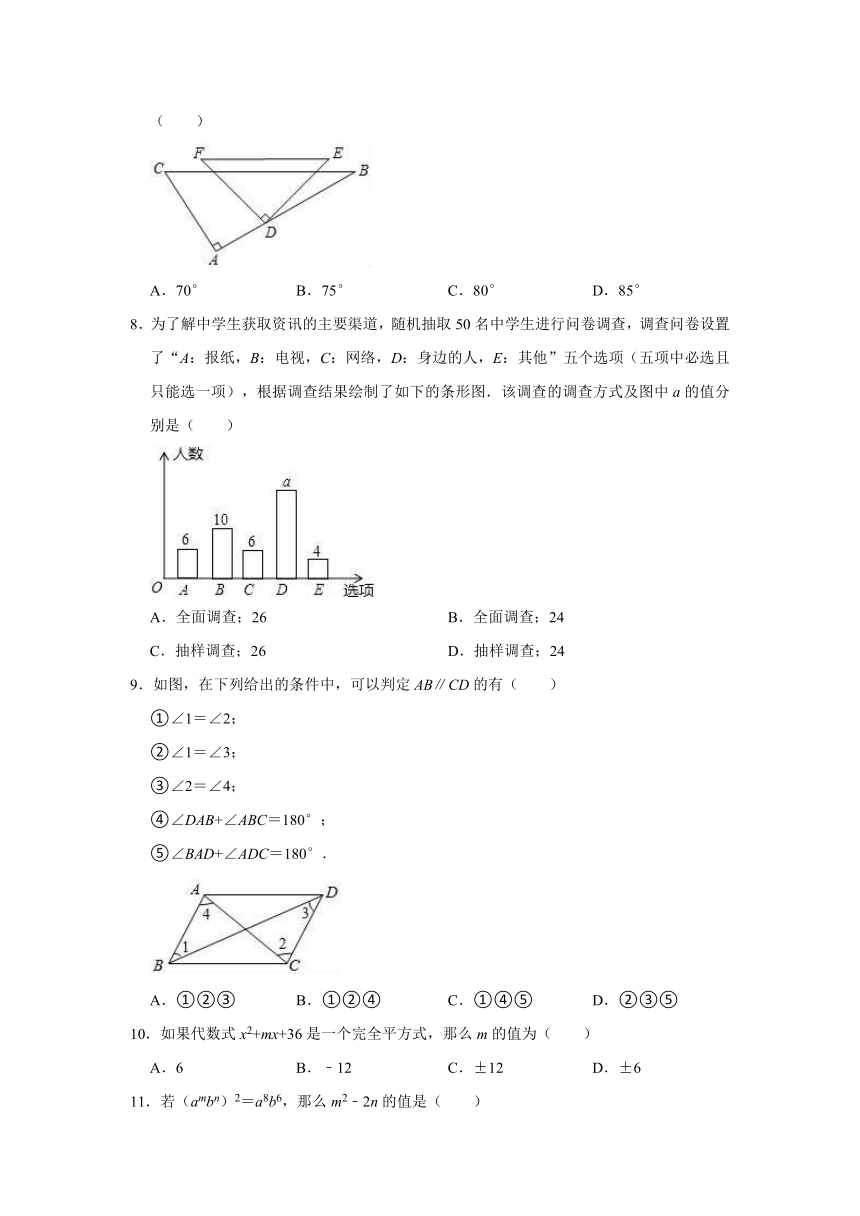
7.将一副直角三角板(∠A=∠FDE=90°,∠F=45°,∠C=60°,点D在边AB上)按图中所示位置摆放,两条斜边为EF,BC,且EF∥BC,则∠ADF等于
( )
A.70°
B.75°
C.80°
D.85°
8.为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该调查的调查方式及图中a的值分别是( )
A.全面调查;26
B.全面调查;24
C.抽样调查;26
D.抽样调查;24
9.如图,在下列给出的条件中,可以判定AB∥CD的有( )
①∠1=∠2;
②∠1=∠3;
③∠2=∠4;
④∠DAB+∠ABC=180°;
⑤∠BAD+∠ADC=180°.
A.①②③
B.①②④
C.①④⑤
D.②③⑤
10.如果代数式x2+mx+36是一个完全平方式,那么m的值为( )
A.6
B.﹣12
C.±12
D.±6
11.若(ambn)2=a8b6,那么m2﹣2n的值是( )
A.10
B.52
C.20
D.32
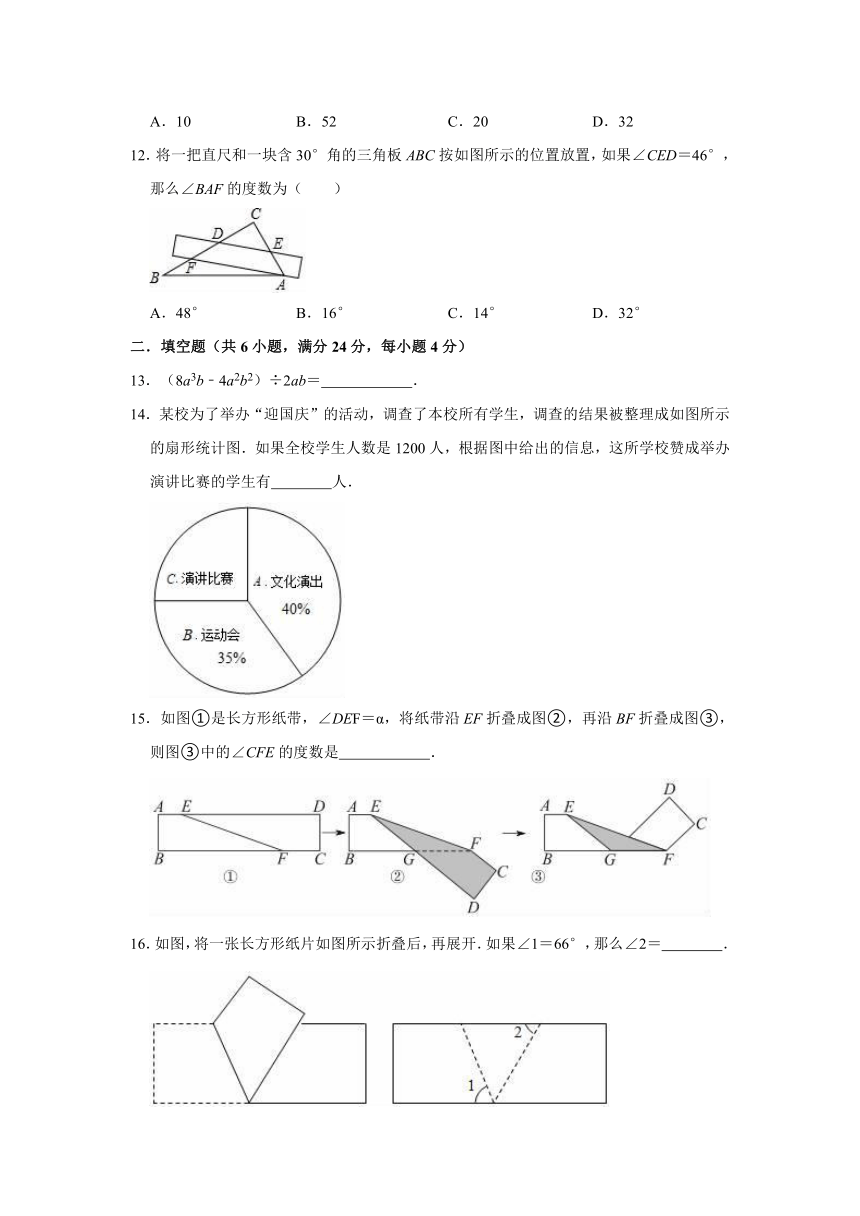
12.将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CED=46°,那么∠BAF的度数为( )
A.48°
B.16°
C.14°
D.32°
二.填空题(共6小题,满分24分,每小题4分)
13.(8a3b﹣4a2b2)÷2ab=
.
14.某校为了举办“迎国庆”的活动,调查了本校所有学生,调查的结果被整理成如图所示的扇形统计图.如果全校学生人数是1200人,根据图中给出的信息,这所学校赞成举办演讲比赛的学生有
人.
15.如图①是长方形纸带,∠DEF=α,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中的∠CFE的度数是
.
16.如图,将一张长方形纸片如图所示折叠后,再展开.如果∠1=66°,那么∠2=
.
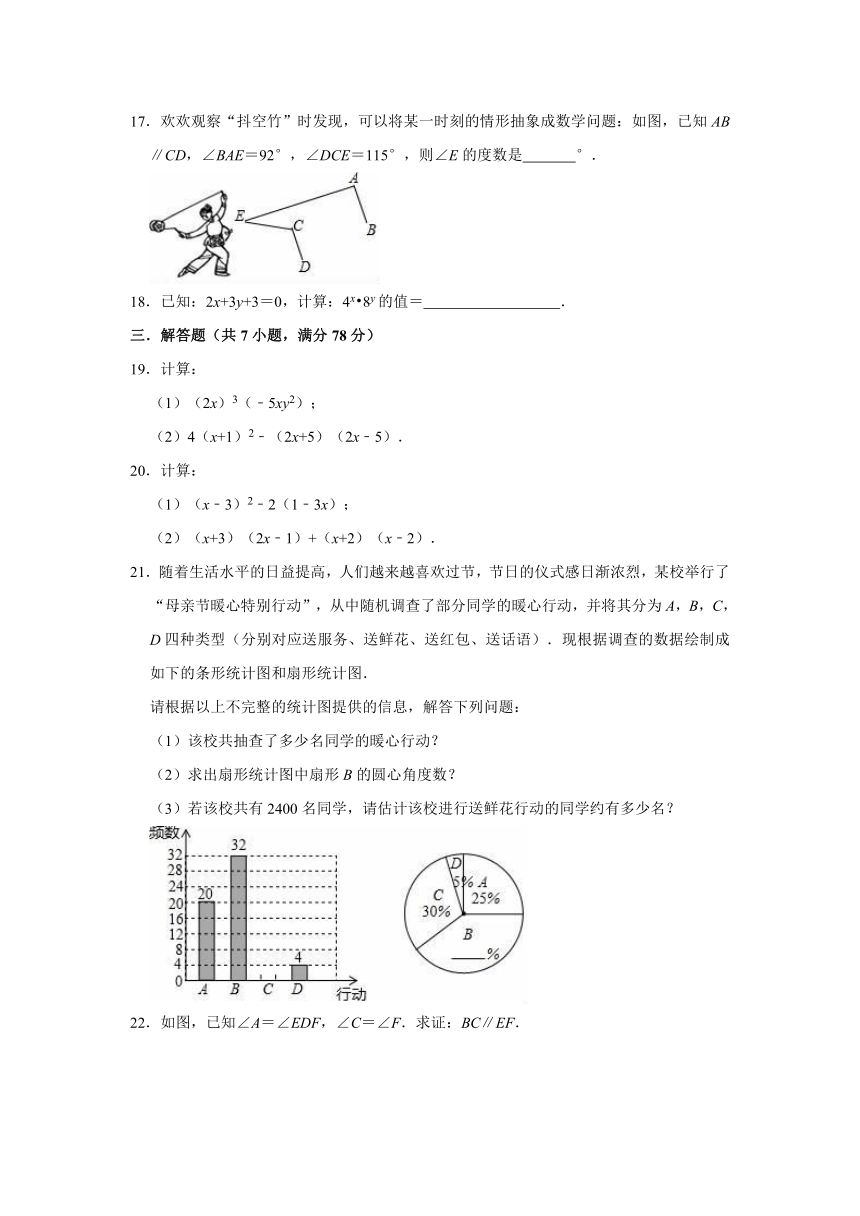
17.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是
°.
18.已知:2x+3y+3=0,计算:4x?8y的值=
.
三.解答题(共7小题,满分78分)
19.计算:
(1)(2x)3(﹣5xy2);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
20.计算:
(1)(x﹣3)2﹣2(1﹣3x);
(2)(x+3)(2x﹣1)+(x+2)(x﹣2).
21.随着生活水平的日益提高,人们越来越喜欢过节,节日的仪式感日渐浓烈,某校举行了“母亲节暖心特别行动”,从中随机调查了部分同学的暖心行动,并将其分为A,B,C,D四种类型(分别对应送服务、送鲜花、送红包、送话语).现根据调查的数据绘制成如下的条形统计图和扇形统计图.
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该校共抽查了多少名同学的暖心行动?
(2)求出扇形统计图中扇形B的圆心角度数?
(3)若该校共有2400名同学,请估计该校进行送鲜花行动的同学约有多少名?
22.如图,已知∠A=∠EDF,∠C=∠F.求证:BC∥EF.
23.先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
24.按要求完成下列证明:
已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知).
∴∠ADC=
.(垂直的定义)
∴∠1+
=90°.
∵∠1+∠2=90°(已知).
∴
=∠2(
).
∴DE∥BC(
).
25.如图,∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
在下列解答中,填空:
证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(
).
∴∠ABC=∠BCD(
).
∵∠P=∠Q(已知),
∴PB∥(
)(
).
∴∠PBC=(
)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(
),∠2=∠BCD﹣(
),
∴∠1=∠2(等量代换).
参考答案与试题解析
一.选择题(共12小题,满分48分,每小题4分)
1.解:A、原式=9a2b4,故A错误.
B、原式=﹣2a2,故B错误.
C、原式=a6﹣a6=0,故C正确.
D、原式=a2+2a+1,故D错误.
故选:C.
2.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
3.A、5a3?3a2=15a5,故选项错误;
B、2x2?5x2=10x4,故选项正确;
C、3x2?2x2=6x4,故选项错误;
D、5y3?3y5=15y8,故选项错误.
故选:B.
4.解:∵AB=10cm,BC=4cm.
∴AC=AB+BC=14cm,
∵D是AC的中点,
∴AD=AC=7cm;
∵M是AB的中点,
∴AM=AB=5cm,
∴DM=AD﹣AM=2cm.
故选:C.
5.解:(a﹣b)(﹣a﹣b)=b2﹣a2,故选项A错误;
2a3+3a3=5a3,故选项B错误;
6x3y2÷3x=2x2y2,故选项C正确;
(﹣2x2)3=﹣8x6,故选项D错误;
故选:C.
6.解:A.这100名考生的数学成绩是总体的一个样本,故本选项不合题意;
B.4300名考生的数学成绩是总体,故本选项不合题意;
C.每位学生的数学成绩是个体,故本选项符合题意;
D.100是样本容量,故本选项不合题意.
故选:C.
7.解:如图所示,CB与FD交点为G,
∵EF∥BC,
∴∠F=∠BGD=45°,
又∵∠ADG是△BDG的外角,∠B=30°,
∴∠ADG=∠B+∠BGD=30°+45°=75°,
故选:B.
8.解:本次调查方式为抽样调查,
a=50﹣6﹣10﹣6﹣4=24,
故选:D.
9.解:①∠1=∠2不能判定AB∥CD,不符合题意;
②∵∠1=∠3,∴AB∥CD,符合题意;
③∵∠2=∠4,∴AB∥CD,符合题意;
④∠DAB+∠ABC=180°;不能判定AB∥CD,不符合题意;
⑤∵∠BAD+∠ADC=180°,∴AB∥CD,符合题意.
故选:D.
10.解:∵x2+mx+36是一个完全平方式,
∴x2+mx+36=(x±6)2,
∴m=±12,
故选:C.
11.解:∵(ambn)2=a2mb2n,
∴a2mb2n=a8b6.
∴2m=8,2n=6.
∴m=4,n=3.
∴m2﹣2n=16﹣6=10.
故选:A.
12.解:∵DE∥AF,
∴∠CED=∠EAF=46°,
∵∠BAC=90°﹣30°=60°,
∴∠BAF=∠BAC﹣∠EAF=60°﹣46°=14°,
故选:C.
二.填空题(共6小题,满分24分,每小题4分)
13.解:(8a3b﹣4a2b2)÷2ab
=8a3b÷2ab﹣4a2b2÷2ab
=4a2﹣2ab.
故答案为:4a2﹣2ab.
14.解:由统计图可得,
这所学校赞成举办演讲比赛的学生有:1200×(1﹣40%﹣35%)=1200×25%=300(人),
故答案为:300.
15.解:∵AD∥BC,
∴∠BFE=∠DEF=α,∠CFE=180°﹣∠DEF=180°﹣α,
∴∠CFG=∠CFE﹣∠BFE=180°﹣α﹣α=180°﹣2α,
∴∠CFE=∠CFG﹣∠BFE=180°﹣2α﹣α=180°﹣3α.
故答案为:180°﹣3α.
16.解:由折叠的性质可知,
∠1=∠3,
∵∠1=66°,
∴∠3=66°,
∵长方形的两条长边平行,
∴∠2+∠1+∠3=180°,
∴∠2=48°,
故答案为:48°.
17.解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=92°,
∴∠CFE=92°,
又∵∠DCE=115°,
∴∠E=∠DCE﹣∠CFE=115°﹣92°=23°.
故答案为:23.
18.解:∵2x+3y+3=0,
∴2x+3y=﹣3,
4x?8y=22x?23y=2(2x+3y)=2﹣3=.
故答案为:.
三.解答题(共7小题,满分78分)
19.解:(1)(2x)3(﹣5xy2)
=8x3?(﹣5xy2)
=﹣40x4y2;
(2)4(x+1)2﹣(2x+5)(2x﹣5)
=4(x2+2x+1)﹣(4x2﹣25)
=4x2+8x+4﹣4x2+25
=8x+29.
20.解:(1)原式=x2﹣6x+9﹣2+6x
=x2+7.
(2)原式=2x2+5x﹣3+x2﹣4
=3x2+5x﹣7.
21.解:(1)20÷25%=80(人),
答:该校共抽查了80名同学的暖心行动.
(2)360°×=144°,
答:扇形统计图中扇形B的圆心角度数为144°.
(3)2400×=960(人),
答:该校2400名同学中进行送鲜花行动的约有960名.
22.证明:∵∠A=∠EDF(已知),
∴AC∥DF(同位角相等,两直线平行),
∴∠C=∠CGF(两直线平行,内错角相等).
又∵∠C=∠F(已知),
∴∠CGF=∠F(等量代换),
∴BC∥EF(内错角相等,两直线平行).
23.解:(1)6x2y(﹣2xy+y3)÷xy2,
=(﹣12x3y2+6x2y4)÷xy2
=﹣12x2+6xy2,
当x=2,y=﹣1时,
原式=﹣12×22+6×2×(﹣1)2
=﹣36;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y)
=x2﹣4y2+x2﹣4xy+4y2﹣3x2+xy
=﹣x2﹣3xy,
当x=﹣2,y=时,
原式=﹣(﹣2)2﹣3×(﹣2)×
=﹣4+3
=﹣1.
24.解:证明:∵CD⊥AB(已知),
∴∠ADC=90°(垂直的定义),
∴∠1+∠CDE=90°,
∵∠1+∠2=90°(已知),
∴∠CDE=∠2(同角的余角相等),
∴DE∥BC(内错角相等,两直线平行),
故答案为:90°;∠CDE;∠CDE,同角的余角相等;内错角相等,两直线平行.
25.证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠P=∠Q(已知),
∴PB∥(CQ)(内错角相等,两直线平行).
∴∠PBC=(∠BCQ)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(∠PBC),∠2=∠BCD﹣(∠BCQ),
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;CQ,内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ.
一.选择题(共12小题,满分48分,每小题4分)
1.下列计算正确的是( )
A.(﹣3ab2)2=6a2b4
B.﹣6a3b÷3ab=﹣2a2b
C.(a2)3﹣(﹣a3)2=0
D.(a+1)2=a2+1
2.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90°
B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180°
D.∠α+∠β+∠γ=180°
3.下列计算中,正确的是( )
A.5a3?3a2=15a6
B.2x2?5x2=10x4
C.3x2?2x2=6x2
D.5y3?3y5=15y15
4.如图,已知直线上顺次三个点A、B、C,已知AB=10cm,BC=4cm.D是AC的中点,M是AB的中点,那么MD=( )cm
A.4
B.3
C.2
D.1
5.下列计算正确的是( )
A.(a﹣b)(﹣a﹣b)=a2﹣b2
B.2a3+3a3=5a6
C.6x3y2÷3x=2x2y2
D.(﹣2x2)3=﹣6x6
6.为了了解我县初一4300名学生在疫情期间“数学空课”的学习情况,全县组织了一次数学检测,从中抽取100名考生的成绩进行统计分析,以下说法正确的是( )
A.这100名考生是总体的一个样本
B.4300名考生是总体
C.每位学生的数学成绩是个体
D.100名学生是样本容量
7.将一副直角三角板(∠A=∠FDE=90°,∠F=45°,∠C=60°,点D在边AB上)按图中所示位置摆放,两条斜边为EF,BC,且EF∥BC,则∠ADF等于
( )
A.70°
B.75°
C.80°
D.85°
8.为了解中学生获取资讯的主要渠道,随机抽取50名中学生进行问卷调查,调查问卷设置了“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项),根据调查结果绘制了如下的条形图.该调查的调查方式及图中a的值分别是( )
A.全面调查;26
B.全面调查;24
C.抽样调查;26
D.抽样调查;24
9.如图,在下列给出的条件中,可以判定AB∥CD的有( )
①∠1=∠2;
②∠1=∠3;
③∠2=∠4;
④∠DAB+∠ABC=180°;
⑤∠BAD+∠ADC=180°.
A.①②③
B.①②④
C.①④⑤
D.②③⑤
10.如果代数式x2+mx+36是一个完全平方式,那么m的值为( )
A.6
B.﹣12
C.±12
D.±6
11.若(ambn)2=a8b6,那么m2﹣2n的值是( )
A.10
B.52
C.20
D.32
12.将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置,如果∠CED=46°,那么∠BAF的度数为( )
A.48°
B.16°
C.14°
D.32°
二.填空题(共6小题,满分24分,每小题4分)
13.(8a3b﹣4a2b2)÷2ab=
.
14.某校为了举办“迎国庆”的活动,调查了本校所有学生,调查的结果被整理成如图所示的扇形统计图.如果全校学生人数是1200人,根据图中给出的信息,这所学校赞成举办演讲比赛的学生有
人.
15.如图①是长方形纸带,∠DEF=α,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中的∠CFE的度数是
.
16.如图,将一张长方形纸片如图所示折叠后,再展开.如果∠1=66°,那么∠2=
.
17.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是
°.
18.已知:2x+3y+3=0,计算:4x?8y的值=
.
三.解答题(共7小题,满分78分)
19.计算:
(1)(2x)3(﹣5xy2);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
20.计算:
(1)(x﹣3)2﹣2(1﹣3x);
(2)(x+3)(2x﹣1)+(x+2)(x﹣2).
21.随着生活水平的日益提高,人们越来越喜欢过节,节日的仪式感日渐浓烈,某校举行了“母亲节暖心特别行动”,从中随机调查了部分同学的暖心行动,并将其分为A,B,C,D四种类型(分别对应送服务、送鲜花、送红包、送话语).现根据调查的数据绘制成如下的条形统计图和扇形统计图.
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该校共抽查了多少名同学的暖心行动?
(2)求出扇形统计图中扇形B的圆心角度数?
(3)若该校共有2400名同学,请估计该校进行送鲜花行动的同学约有多少名?
22.如图,已知∠A=∠EDF,∠C=∠F.求证:BC∥EF.
23.先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
24.按要求完成下列证明:
已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知).
∴∠ADC=
.(垂直的定义)
∴∠1+
=90°.
∵∠1+∠2=90°(已知).
∴
=∠2(
).
∴DE∥BC(
).
25.如图,∠ABC+∠ECB=180°,∠P=∠Q.求证:∠1=∠2.
在下列解答中,填空:
证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(
).
∴∠ABC=∠BCD(
).
∵∠P=∠Q(已知),
∴PB∥(
)(
).
∴∠PBC=(
)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(
),∠2=∠BCD﹣(
),
∴∠1=∠2(等量代换).
参考答案与试题解析
一.选择题(共12小题,满分48分,每小题4分)
1.解:A、原式=9a2b4,故A错误.
B、原式=﹣2a2,故B错误.
C、原式=a6﹣a6=0,故C正确.
D、原式=a2+2a+1,故D错误.
故选:C.
2.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
3.A、5a3?3a2=15a5,故选项错误;
B、2x2?5x2=10x4,故选项正确;
C、3x2?2x2=6x4,故选项错误;
D、5y3?3y5=15y8,故选项错误.
故选:B.
4.解:∵AB=10cm,BC=4cm.
∴AC=AB+BC=14cm,
∵D是AC的中点,
∴AD=AC=7cm;
∵M是AB的中点,
∴AM=AB=5cm,
∴DM=AD﹣AM=2cm.
故选:C.
5.解:(a﹣b)(﹣a﹣b)=b2﹣a2,故选项A错误;
2a3+3a3=5a3,故选项B错误;
6x3y2÷3x=2x2y2,故选项C正确;
(﹣2x2)3=﹣8x6,故选项D错误;
故选:C.
6.解:A.这100名考生的数学成绩是总体的一个样本,故本选项不合题意;
B.4300名考生的数学成绩是总体,故本选项不合题意;
C.每位学生的数学成绩是个体,故本选项符合题意;
D.100是样本容量,故本选项不合题意.
故选:C.
7.解:如图所示,CB与FD交点为G,
∵EF∥BC,
∴∠F=∠BGD=45°,
又∵∠ADG是△BDG的外角,∠B=30°,
∴∠ADG=∠B+∠BGD=30°+45°=75°,
故选:B.
8.解:本次调查方式为抽样调查,
a=50﹣6﹣10﹣6﹣4=24,
故选:D.
9.解:①∠1=∠2不能判定AB∥CD,不符合题意;
②∵∠1=∠3,∴AB∥CD,符合题意;
③∵∠2=∠4,∴AB∥CD,符合题意;
④∠DAB+∠ABC=180°;不能判定AB∥CD,不符合题意;
⑤∵∠BAD+∠ADC=180°,∴AB∥CD,符合题意.
故选:D.
10.解:∵x2+mx+36是一个完全平方式,
∴x2+mx+36=(x±6)2,
∴m=±12,
故选:C.
11.解:∵(ambn)2=a2mb2n,
∴a2mb2n=a8b6.
∴2m=8,2n=6.
∴m=4,n=3.
∴m2﹣2n=16﹣6=10.
故选:A.
12.解:∵DE∥AF,
∴∠CED=∠EAF=46°,
∵∠BAC=90°﹣30°=60°,
∴∠BAF=∠BAC﹣∠EAF=60°﹣46°=14°,
故选:C.
二.填空题(共6小题,满分24分,每小题4分)
13.解:(8a3b﹣4a2b2)÷2ab
=8a3b÷2ab﹣4a2b2÷2ab
=4a2﹣2ab.
故答案为:4a2﹣2ab.
14.解:由统计图可得,
这所学校赞成举办演讲比赛的学生有:1200×(1﹣40%﹣35%)=1200×25%=300(人),
故答案为:300.
15.解:∵AD∥BC,
∴∠BFE=∠DEF=α,∠CFE=180°﹣∠DEF=180°﹣α,
∴∠CFG=∠CFE﹣∠BFE=180°﹣α﹣α=180°﹣2α,
∴∠CFE=∠CFG﹣∠BFE=180°﹣2α﹣α=180°﹣3α.
故答案为:180°﹣3α.
16.解:由折叠的性质可知,
∠1=∠3,
∵∠1=66°,
∴∠3=66°,
∵长方形的两条长边平行,
∴∠2+∠1+∠3=180°,
∴∠2=48°,
故答案为:48°.
17.解:如图,延长DC交AE于F,
∵AB∥CD,∠BAE=92°,
∴∠CFE=92°,
又∵∠DCE=115°,
∴∠E=∠DCE﹣∠CFE=115°﹣92°=23°.
故答案为:23.
18.解:∵2x+3y+3=0,
∴2x+3y=﹣3,
4x?8y=22x?23y=2(2x+3y)=2﹣3=.
故答案为:.
三.解答题(共7小题,满分78分)
19.解:(1)(2x)3(﹣5xy2)
=8x3?(﹣5xy2)
=﹣40x4y2;
(2)4(x+1)2﹣(2x+5)(2x﹣5)
=4(x2+2x+1)﹣(4x2﹣25)
=4x2+8x+4﹣4x2+25
=8x+29.
20.解:(1)原式=x2﹣6x+9﹣2+6x
=x2+7.
(2)原式=2x2+5x﹣3+x2﹣4
=3x2+5x﹣7.
21.解:(1)20÷25%=80(人),
答:该校共抽查了80名同学的暖心行动.
(2)360°×=144°,
答:扇形统计图中扇形B的圆心角度数为144°.
(3)2400×=960(人),
答:该校2400名同学中进行送鲜花行动的约有960名.
22.证明:∵∠A=∠EDF(已知),
∴AC∥DF(同位角相等,两直线平行),
∴∠C=∠CGF(两直线平行,内错角相等).
又∵∠C=∠F(已知),
∴∠CGF=∠F(等量代换),
∴BC∥EF(内错角相等,两直线平行).
23.解:(1)6x2y(﹣2xy+y3)÷xy2,
=(﹣12x3y2+6x2y4)÷xy2
=﹣12x2+6xy2,
当x=2,y=﹣1时,
原式=﹣12×22+6×2×(﹣1)2
=﹣36;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y)
=x2﹣4y2+x2﹣4xy+4y2﹣3x2+xy
=﹣x2﹣3xy,
当x=﹣2,y=时,
原式=﹣(﹣2)2﹣3×(﹣2)×
=﹣4+3
=﹣1.
24.解:证明:∵CD⊥AB(已知),
∴∠ADC=90°(垂直的定义),
∴∠1+∠CDE=90°,
∵∠1+∠2=90°(已知),
∴∠CDE=∠2(同角的余角相等),
∴DE∥BC(内错角相等,两直线平行),
故答案为:90°;∠CDE;∠CDE,同角的余角相等;内错角相等,两直线平行.
25.证明:∵∠ABC+∠ECB=180°(已知),
∴AB∥DE(同旁内角互补,两直线平行).
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠P=∠Q(已知),
∴PB∥(CQ)(内错角相等,两直线平行).
∴∠PBC=(∠BCQ)(两直线平行,内错角相等).
∵∠1=∠ABC﹣(∠PBC),∠2=∠BCD﹣(∠BCQ),
∴∠1=∠2(等量代换).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;CQ,内错角相等,两直线平行;∠BCQ;∠PBC;∠BCQ.
同课章节目录
