2020-2021学年鲁教五四新版七年级下册数学期末冲刺试题(word解析版)
文档属性
| 名称 | 2020-2021学年鲁教五四新版七年级下册数学期末冲刺试题(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 281.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 16:46:27 | ||
图片预览




文档简介
2020-2021学年鲁教五四新版七年级下册数学期末冲刺试题
一.选择题(共12小题,满分48分,每小题4分)
1.下列选项是二元一次方程组的是( )
A.
B.
C.
D.
2.在某个常规赛季中,科比罚球投篮的命中率大约是83.3%,下列说法错误的是( )
A.科比罚球投篮2次,一定全部命中
B.科比罚球投篮2次,不一定全部命中
C.科比罚球投篮1次,命中的可能性较大
D.科比罚球投篮1次,不命中的可能性较小
3.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )
A.
B.
C.
D.
4.气象台预明天下雨的概率为70%,则下列理解正确的是( )
A.明天30%的地区不会下雨
B.明天下雨的可能性较大
C.明天70%的时间会下雨
D.明天下雨是必然事件
5.已知关于x、y的方程x2m﹣n﹣2+ym+n+1=6是二元一次方程,则m,n的值为( )
A.m=1,n=﹣1
B.m=﹣1,n=1
C.m=,n=﹣
D.m=﹣,n=
6.如图,△ABC中,AB=AC,AD是∠BAC的平分线,已知AB=5,AD=3,则BC的长为( )
A.5
B.4
C.10
D.8
7.如图,正方形边长为2,分别以正方形的两个对角顶点为圆心,以2为半径画弧,构成如图的阴影部分,若在该正方形内随意抛一粒豆子,则豆子落在阴影部分的概率为( )
A.
B.π﹣2
C.π
D.
8.如图,Rt△ABC中,∠B=90°,ED垂直平分AC,ED交AC于点D,交BC于点E.已知△ABC的周长为24,△ABE的周长为14,则AC的长度为( )
A.10
B.14
C.24
D.25
9.用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是( )
A.SAS
B.ASA
C.AAS
D.SSS
10.《九章算术》中记载“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?此问题中羊价为( )
A.160钱
B.155钱
C.150钱
D.145钱
11.用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中( )
A.至少有两个内角是直角
B.没有一个内角是直角
C.至少有一个内角是直角
D.每一个内角都不是直角
12.若不等式组无解,则a的取值范围是( )
A.a≤1
B.a>1
C.a≥1
D.a<1
二.填空题(共6小题,满分24分,每小题4分)
13.关于x的不等式2x﹣a≤﹣1的解集如图所示,则a的值是
.
14.若关于x的不等式x﹣a>0恰好有两个负整数解,则a的范围为
.
15.如图,已知∠ACP=115°,∠B=65°,则∠A=
.
16.书架上有两套两样的教材,每套分上、下两册,在这四册教材中随机抽取两册,恰好组成一套教材的概率是
.
17.命题:“平行于同一条直线的两条直线平行”的题设是
,结论是
.
18.如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An.设∠A=θ.则:
(1)∠A1=
;
(2)∠An=
.
三.解答题(共7小题,满分78分)
19.解方程组:
(1)(代入法);
(2)(加减法).
20.解不等式组并在数轴上表示解集.
21.如图,在△ABC中,D是BC上一点,若AB=10,BD=6,AD=8,AC=17.
(1)求DC的长.
(2)求△ABC的面积.
22.为了缓解新冠病毒疫情带来的影响,某商场设立了一个可以自由转动的转盘吸引顾客,并规定:顾客每购买100元商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券.(转盘等分成16个扇形),如果冲冲的妈妈购物120元.
(1)她获得购物券的概率是多少?
(2)冲冲的妈妈获得100元、50元、20元购物券的概率分别是多少?
23.如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD;
(2)如图2,点F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数.
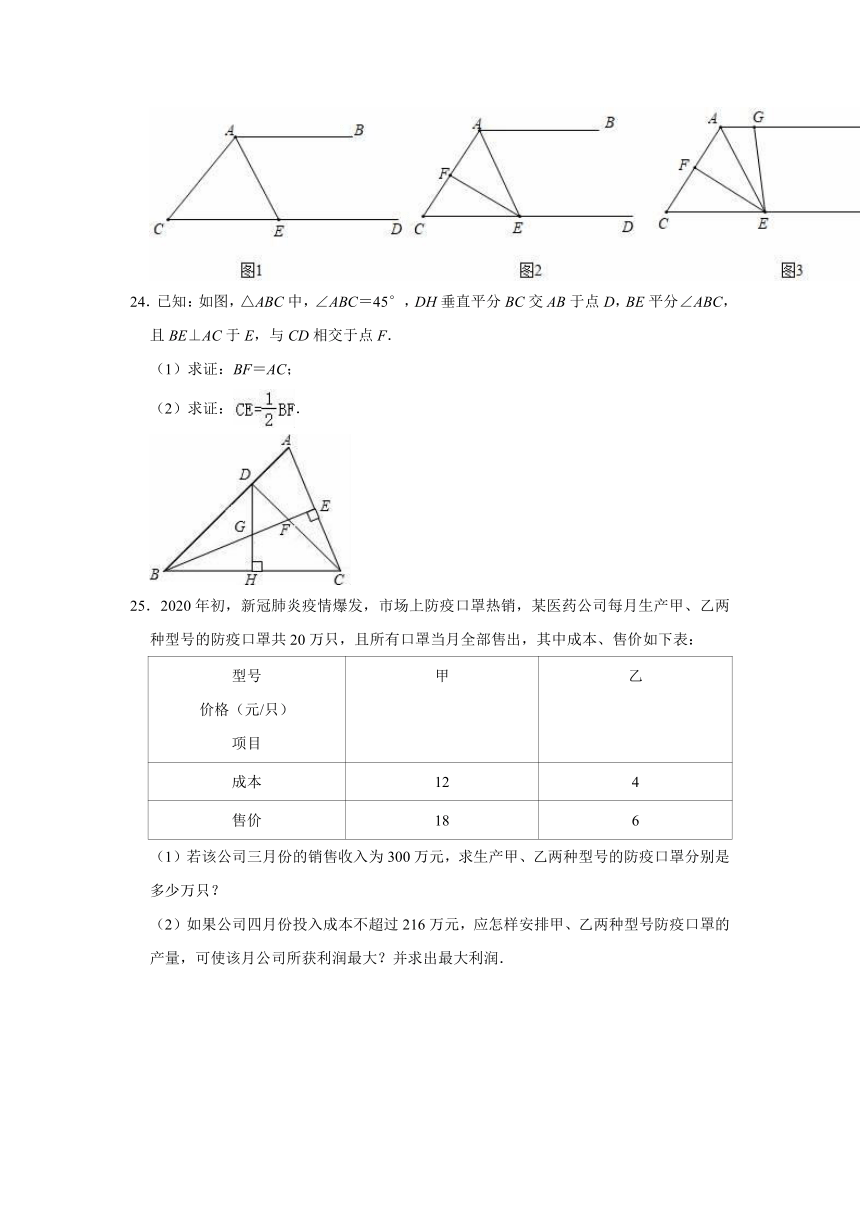
24.已知:如图,△ABC中,∠ABC=45°,DH垂直平分BC交AB于点D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F.
(1)求证:BF=AC;
(2)求证:.
25.2020年初,新冠肺炎疫情爆发,市场上防疫口罩热销,某医药公司每月生产甲、乙两种型号的防疫口罩共20万只,且所有口罩当月全部售出,其中成本、售价如下表:
型号价格(元/只)项目
甲
乙
成本
12
4
售价
18
6
(1)若该公司三月份的销售收入为300万元,求生产甲、乙两种型号的防疫口罩分别是多少万只?
(2)如果公司四月份投入成本不超过216万元,应怎样安排甲、乙两种型号防疫口罩的产量,可使该月公司所获利润最大?并求出最大利润.
参考答案与试题解析
一.选择题(共12小题,满分48分,每小题4分)
1.解:A、含有3个未知数,不是二元一次方程组,故此选项不合题意;
B、是二元一次方程组,故此选项符合题意;
C、含有3个未知数,不是二元一次方程组,故此选项不合题意;
D、含有分式,不是二元一次方程组,故此选项不合题意;
故选:B.
2.解:科比罚球投篮的命中率大约是83.3%,
科比罚球投篮2次,不一定全部命中,A选项错误、B选项正确;
科比罚球投篮1次,命中的可能性较大、不命中的可能性较小,C、D选项说法正确;
故选:A.
3.解:因为函数图象交点坐标为两函数解析式组成的方程组的解.
因此方程组的解是;
故选:B.
4.解:天气台预报明天下雨的概率为70%,说明明天下雨的可能性很大,故B正确.
故选:B.
5.解:∵关于x、y的方程x2m﹣n﹣2+ym+n+1=6是二元一次方程,
∴,
解得.
故选:A.
6.解:∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,BD=CD,
∵AB=5,AD=3,
∴BD==4,
∴BC=2BD=8,
故选:D.
7.解:S阴影=2S扇形﹣S正方形=2×﹣22=π×22﹣22=2(π﹣2).
所以在该正方形内随意抛一粒豆子,则豆子落在阴影部分的概率为=,
故选:A.
8.解:∵ED垂直平分AC,
∴EA=EC,
∵△ABC的周长为24,
∴AB+BC+AC=24,
∵△ABE的周长为14,
∴AB+BE+EA=AB+BE+EC=AB+BC=14,
∴AC=24﹣14=10,
故选:A.
9.解:设已知角为∠O,以顶点O为圆心,任意长为半径画弧,交角的两边分别为A,B两点;
画一条射线b,端点为M;
以M为圆心,OA长为半径画弧,交射线b于C点;以C为圆心,AB长为半径画弧,两弧交于点D;
作射线MD.
则∠COD就是所求的角.
由以上过程不难看出两个三角形中有三条边对应相等,
∴证明全等的方法是SSS.
故选:D.
10.解:设共有x人合伙买羊,羊价为y钱,
依题意,得:,
解得:.
故选:C.
11.解:用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中至少有两个内角是直角,
故选:A.
12.解:不等式组整理得:,
由不等式组无解,得到a+1≥2.
∴a≥1,
故选:C.
二.填空题(共6小题,满分24分,每小题4分)
13.解:2x﹣a≤﹣1,
2x≤a﹣1,
x≤,
∵x≤﹣1,
∴=﹣1,
解得:a=﹣1,
故答案为:﹣1.
14.解:∵x﹣a>0,
∴x>a,
∵不等式x﹣a>0恰有两个负整数解,
∴﹣3≤a<﹣2.
故答案为﹣3≤a<﹣2.
15.解:∵∠ACP=115°,∠B=65°,
∴∠A=∠ACP﹣∠B=115°﹣65°=50°.
故答案为:50°.
16.解:设第一套教材上册为a,下册为b,第二套教材为上册为x,下册为y.
共有12种情况,
恰好组成一套教材的情况数有4种,
所以能组成一套教材的概率为,
故答案为.
17.解:命题:“平行于同一条直线的两条直线平行”的题设是两条直线平行于同一条直线,结论是这两条直线平行.
18.解:(1)∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
∵∠A=θ,
∴∠A1=;
(2)同理可得∠A2=∠A1=?θ=,
所以∠An=.
故答案为:(1),(2).
三.解答题(共7小题,满分78分)
19.解:(1),
由①得:y=4﹣x③,
将③代入②得,
3x﹣2(4﹣x)=2,
5x﹣8=2,
5x=10,
x=2,
将x=2代入①得,
y=2,
∴方程组的解为:,
(2),
将①×2+②得,
5x=10,
x=2,
将x=2代入①得,
y=3,
∴方程组的解为:.
20.解:解不等式2x+1>0,得:x>﹣,
解不等式≥,得:x≤0,
则不等式组的解集为﹣<x≤0,
将不等式组的解集表示在数轴上如下:
21.解:(1)在△ABD中,AB=10,BD=6,AD=8,
∴AB2=BD2+AD2,
∴△ABD为直角三角形,
∴AD⊥BC,即∠ADC=90°,
在Rt△ADC中,AD=8,AC=17,
根据勾股定理得:DC==15;
(2)S△ABC=AD?BC=AD?(BD+DC)=84.
22.解:(1)她获得购物券的概率=;
(2)冲冲的妈妈获得100元的概率=;冲冲的妈妈获得50元的概率==;冲冲的妈妈获得20元的概率==.
23.(1)证明:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD;
(2)证明:过F作FM∥AB,如图,
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFM=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°;
(3)解:设∠GEF=∠C=x°,
∵∠GEF=∠C,∠GED=2∠GEF,
∴∠GED=2x°,
∵AB∥CD,
∴∠C+∠BAC=180°,
∴∠BAC=180°﹣x°,
∵AE平分∠BAC,
∴∠BAE=BAC=(180°﹣x°)=90°﹣x°,
由(1)知:AB∥CD,
∴∠BAE+∠AED=180°,
∵∠AEF=35°,
∴90﹣x+x﹣35+2x=180,
解得:x=50,
即∠C=50°.
24.证明:(1)∵DH垂直平分BC,且∠ABC=45°,
∴BD=DC,且∠BDC=90°,
∵∠A+∠ABF=90°,∠A+∠ACD=90°,
∴∠ABF=∠ACD,
在△BDF和△CDA中,
,
∴△BDF≌△CDA(ASA),
∴BF=AC.
(2)由(1)得BF=AC,
∵BE平分∠ABC,且BE⊥AC,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(ASA),
∴CE=AE=AC=BF.
25.解:(1)设生产甲、乙两种型号的防疫口罩分别是x万只和y万只,
由题意可得:,
解得:,
答:生产甲、乙两种型号的防疫口罩分别是15万只和5万只;
(2)设四月份生产甲、乙两种型号的防疫口罩分别是a万只和(20﹣a)万只,利润为w万元,
由题意可得:12a+4(20﹣a)≤216,
∴a≤17,
∵w=(18﹣12)a+(6﹣4)(20﹣a)=4a+40是一次函数,w随a的增大而增大,
∴a=17时,w有最大利润=108(万元),
答:安排生产甲种型号的防疫口罩17万只,乙种型号的防疫口罩3万只,最大利润为108万元.
一.选择题(共12小题,满分48分,每小题4分)
1.下列选项是二元一次方程组的是( )
A.
B.
C.
D.
2.在某个常规赛季中,科比罚球投篮的命中率大约是83.3%,下列说法错误的是( )
A.科比罚球投篮2次,一定全部命中
B.科比罚球投篮2次,不一定全部命中
C.科比罚球投篮1次,命中的可能性较大
D.科比罚球投篮1次,不命中的可能性较小
3.如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )
A.
B.
C.
D.
4.气象台预明天下雨的概率为70%,则下列理解正确的是( )
A.明天30%的地区不会下雨
B.明天下雨的可能性较大
C.明天70%的时间会下雨
D.明天下雨是必然事件
5.已知关于x、y的方程x2m﹣n﹣2+ym+n+1=6是二元一次方程,则m,n的值为( )
A.m=1,n=﹣1
B.m=﹣1,n=1
C.m=,n=﹣
D.m=﹣,n=
6.如图,△ABC中,AB=AC,AD是∠BAC的平分线,已知AB=5,AD=3,则BC的长为( )
A.5
B.4
C.10
D.8
7.如图,正方形边长为2,分别以正方形的两个对角顶点为圆心,以2为半径画弧,构成如图的阴影部分,若在该正方形内随意抛一粒豆子,则豆子落在阴影部分的概率为( )
A.
B.π﹣2
C.π
D.
8.如图,Rt△ABC中,∠B=90°,ED垂直平分AC,ED交AC于点D,交BC于点E.已知△ABC的周长为24,△ABE的周长为14,则AC的长度为( )
A.10
B.14
C.24
D.25
9.用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其运用全等的方法是( )
A.SAS
B.ASA
C.AAS
D.SSS
10.《九章算术》中记载“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?此问题中羊价为( )
A.160钱
B.155钱
C.150钱
D.145钱
11.用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中( )
A.至少有两个内角是直角
B.没有一个内角是直角
C.至少有一个内角是直角
D.每一个内角都不是直角
12.若不等式组无解,则a的取值范围是( )
A.a≤1
B.a>1
C.a≥1
D.a<1
二.填空题(共6小题,满分24分,每小题4分)
13.关于x的不等式2x﹣a≤﹣1的解集如图所示,则a的值是
.
14.若关于x的不等式x﹣a>0恰好有两个负整数解,则a的范围为
.
15.如图,已知∠ACP=115°,∠B=65°,则∠A=
.
16.书架上有两套两样的教材,每套分上、下两册,在这四册教材中随机抽取两册,恰好组成一套教材的概率是
.
17.命题:“平行于同一条直线的两条直线平行”的题设是
,结论是
.
18.如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An.设∠A=θ.则:
(1)∠A1=
;
(2)∠An=
.
三.解答题(共7小题,满分78分)
19.解方程组:
(1)(代入法);
(2)(加减法).
20.解不等式组并在数轴上表示解集.
21.如图,在△ABC中,D是BC上一点,若AB=10,BD=6,AD=8,AC=17.
(1)求DC的长.
(2)求△ABC的面积.
22.为了缓解新冠病毒疫情带来的影响,某商场设立了一个可以自由转动的转盘吸引顾客,并规定:顾客每购买100元商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得100元、50元、20元的购物券.(转盘等分成16个扇形),如果冲冲的妈妈购物120元.
(1)她获得购物券的概率是多少?
(2)冲冲的妈妈获得100元、50元、20元购物券的概率分别是多少?
23.如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD;
(2)如图2,点F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数.
24.已知:如图,△ABC中,∠ABC=45°,DH垂直平分BC交AB于点D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F.
(1)求证:BF=AC;
(2)求证:.
25.2020年初,新冠肺炎疫情爆发,市场上防疫口罩热销,某医药公司每月生产甲、乙两种型号的防疫口罩共20万只,且所有口罩当月全部售出,其中成本、售价如下表:
型号价格(元/只)项目
甲
乙
成本
12
4
售价
18
6
(1)若该公司三月份的销售收入为300万元,求生产甲、乙两种型号的防疫口罩分别是多少万只?
(2)如果公司四月份投入成本不超过216万元,应怎样安排甲、乙两种型号防疫口罩的产量,可使该月公司所获利润最大?并求出最大利润.
参考答案与试题解析
一.选择题(共12小题,满分48分,每小题4分)
1.解:A、含有3个未知数,不是二元一次方程组,故此选项不合题意;
B、是二元一次方程组,故此选项符合题意;
C、含有3个未知数,不是二元一次方程组,故此选项不合题意;
D、含有分式,不是二元一次方程组,故此选项不合题意;
故选:B.
2.解:科比罚球投篮的命中率大约是83.3%,
科比罚球投篮2次,不一定全部命中,A选项错误、B选项正确;
科比罚球投篮1次,命中的可能性较大、不命中的可能性较小,C、D选项说法正确;
故选:A.
3.解:因为函数图象交点坐标为两函数解析式组成的方程组的解.
因此方程组的解是;
故选:B.
4.解:天气台预报明天下雨的概率为70%,说明明天下雨的可能性很大,故B正确.
故选:B.
5.解:∵关于x、y的方程x2m﹣n﹣2+ym+n+1=6是二元一次方程,
∴,
解得.
故选:A.
6.解:∵AB=AC,AD是∠BAC的平分线,
∴AD⊥BC,BD=CD,
∵AB=5,AD=3,
∴BD==4,
∴BC=2BD=8,
故选:D.
7.解:S阴影=2S扇形﹣S正方形=2×﹣22=π×22﹣22=2(π﹣2).
所以在该正方形内随意抛一粒豆子,则豆子落在阴影部分的概率为=,
故选:A.
8.解:∵ED垂直平分AC,
∴EA=EC,
∵△ABC的周长为24,
∴AB+BC+AC=24,
∵△ABE的周长为14,
∴AB+BE+EA=AB+BE+EC=AB+BC=14,
∴AC=24﹣14=10,
故选:A.
9.解:设已知角为∠O,以顶点O为圆心,任意长为半径画弧,交角的两边分别为A,B两点;
画一条射线b,端点为M;
以M为圆心,OA长为半径画弧,交射线b于C点;以C为圆心,AB长为半径画弧,两弧交于点D;
作射线MD.
则∠COD就是所求的角.
由以上过程不难看出两个三角形中有三条边对应相等,
∴证明全等的方法是SSS.
故选:D.
10.解:设共有x人合伙买羊,羊价为y钱,
依题意,得:,
解得:.
故选:C.
11.解:用反证法证明“三角形中最多有一个内角是直角”应先假设这个三角形中至少有两个内角是直角,
故选:A.
12.解:不等式组整理得:,
由不等式组无解,得到a+1≥2.
∴a≥1,
故选:C.
二.填空题(共6小题,满分24分,每小题4分)
13.解:2x﹣a≤﹣1,
2x≤a﹣1,
x≤,
∵x≤﹣1,
∴=﹣1,
解得:a=﹣1,
故答案为:﹣1.
14.解:∵x﹣a>0,
∴x>a,
∵不等式x﹣a>0恰有两个负整数解,
∴﹣3≤a<﹣2.
故答案为﹣3≤a<﹣2.
15.解:∵∠ACP=115°,∠B=65°,
∴∠A=∠ACP﹣∠B=115°﹣65°=50°.
故答案为:50°.
16.解:设第一套教材上册为a,下册为b,第二套教材为上册为x,下册为y.
共有12种情况,
恰好组成一套教材的情况数有4种,
所以能组成一套教材的概率为,
故答案为.
17.解:命题:“平行于同一条直线的两条直线平行”的题设是两条直线平行于同一条直线,结论是这两条直线平行.
18.解:(1)∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
∵∠A=θ,
∴∠A1=;
(2)同理可得∠A2=∠A1=?θ=,
所以∠An=.
故答案为:(1),(2).
三.解答题(共7小题,满分78分)
19.解:(1),
由①得:y=4﹣x③,
将③代入②得,
3x﹣2(4﹣x)=2,
5x﹣8=2,
5x=10,
x=2,
将x=2代入①得,
y=2,
∴方程组的解为:,
(2),
将①×2+②得,
5x=10,
x=2,
将x=2代入①得,
y=3,
∴方程组的解为:.
20.解:解不等式2x+1>0,得:x>﹣,
解不等式≥,得:x≤0,
则不等式组的解集为﹣<x≤0,
将不等式组的解集表示在数轴上如下:
21.解:(1)在△ABD中,AB=10,BD=6,AD=8,
∴AB2=BD2+AD2,
∴△ABD为直角三角形,
∴AD⊥BC,即∠ADC=90°,
在Rt△ADC中,AD=8,AC=17,
根据勾股定理得:DC==15;
(2)S△ABC=AD?BC=AD?(BD+DC)=84.
22.解:(1)她获得购物券的概率=;
(2)冲冲的妈妈获得100元的概率=;冲冲的妈妈获得50元的概率==;冲冲的妈妈获得20元的概率==.
23.(1)证明:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD;
(2)证明:过F作FM∥AB,如图,
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFM=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°;
(3)解:设∠GEF=∠C=x°,
∵∠GEF=∠C,∠GED=2∠GEF,
∴∠GED=2x°,
∵AB∥CD,
∴∠C+∠BAC=180°,
∴∠BAC=180°﹣x°,
∵AE平分∠BAC,
∴∠BAE=BAC=(180°﹣x°)=90°﹣x°,
由(1)知:AB∥CD,
∴∠BAE+∠AED=180°,
∵∠AEF=35°,
∴90﹣x+x﹣35+2x=180,
解得:x=50,
即∠C=50°.
24.证明:(1)∵DH垂直平分BC,且∠ABC=45°,
∴BD=DC,且∠BDC=90°,
∵∠A+∠ABF=90°,∠A+∠ACD=90°,
∴∠ABF=∠ACD,
在△BDF和△CDA中,
,
∴△BDF≌△CDA(ASA),
∴BF=AC.
(2)由(1)得BF=AC,
∵BE平分∠ABC,且BE⊥AC,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(ASA),
∴CE=AE=AC=BF.
25.解:(1)设生产甲、乙两种型号的防疫口罩分别是x万只和y万只,
由题意可得:,
解得:,
答:生产甲、乙两种型号的防疫口罩分别是15万只和5万只;
(2)设四月份生产甲、乙两种型号的防疫口罩分别是a万只和(20﹣a)万只,利润为w万元,
由题意可得:12a+4(20﹣a)≤216,
∴a≤17,
∵w=(18﹣12)a+(6﹣4)(20﹣a)=4a+40是一次函数,w随a的增大而增大,
∴a=17时,w有最大利润=108(万元),
答:安排生产甲种型号的防疫口罩17万只,乙种型号的防疫口罩3万只,最大利润为108万元.
同课章节目录
