沪科版九年级数学上册23.1 锐角的三角函数课件(22张)
文档属性
| 名称 | 沪科版九年级数学上册23.1 锐角的三角函数课件(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 09:08:43 | ||
图片预览




文档简介
(共22张PPT)
沪科版九年级数学上册第二十三章
1
2
哪个轨道更陡?
你是如何判断的?
A
B
C
D
E
F
情境导入
3
探索新知
我们都有过走上坡路的经验,坡面有陡有平,在数学上该如何衡量坡面的倾斜程度呢?如图所示:
(二)
(一)
(1)
(1)
(2)
(2)
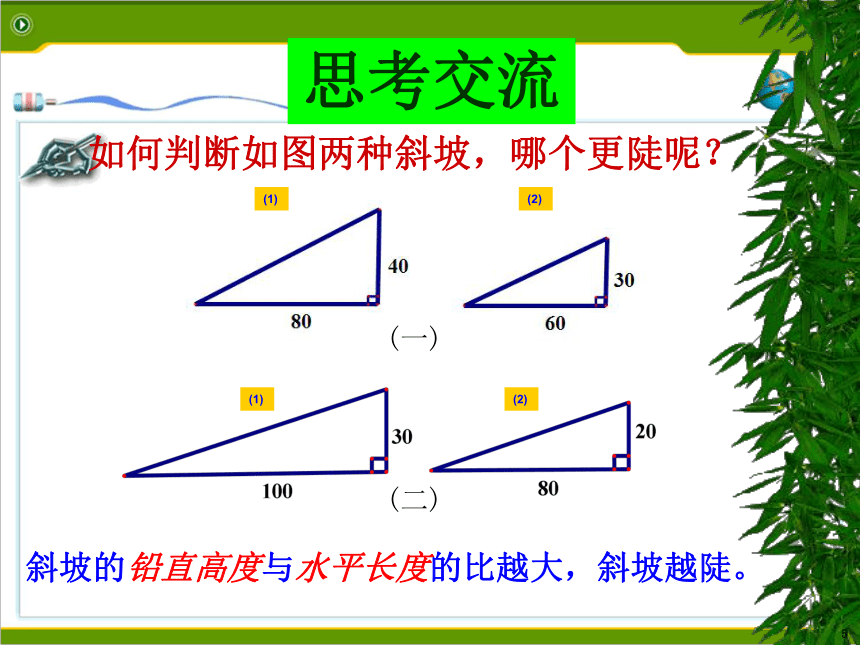
铅直高度
水平长度
4
如何判断如图两种斜坡,哪个更陡呢?
(1)
(2)
斜坡的铅直高度与水平长度的比越大,斜坡越陡。
5
思考交流
(1)
(2)
(一)
(二)
B1
C1
B2
C2
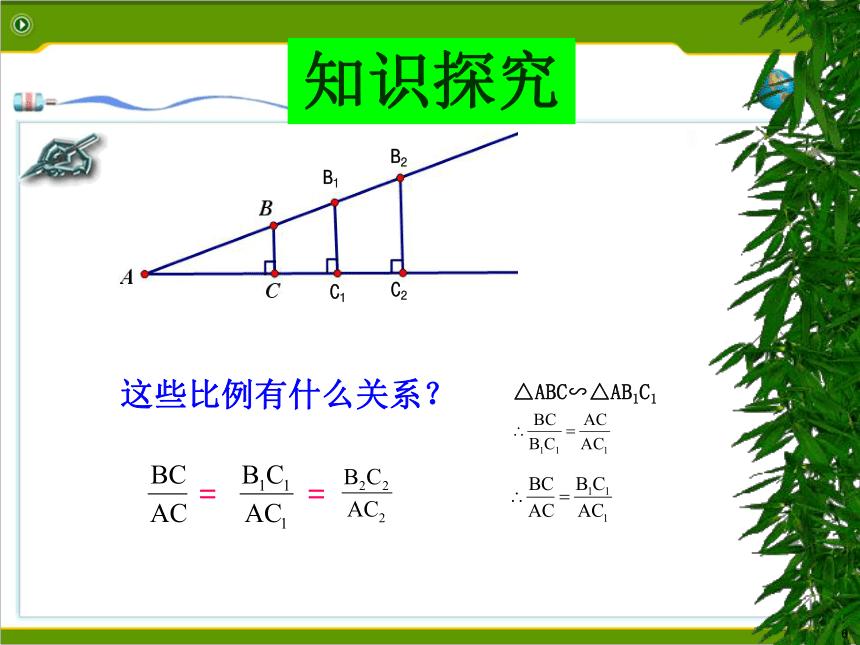
这些比例有什么关系?
=
=
△ABC∽△AB1C1
知识探究
6
B1
C1
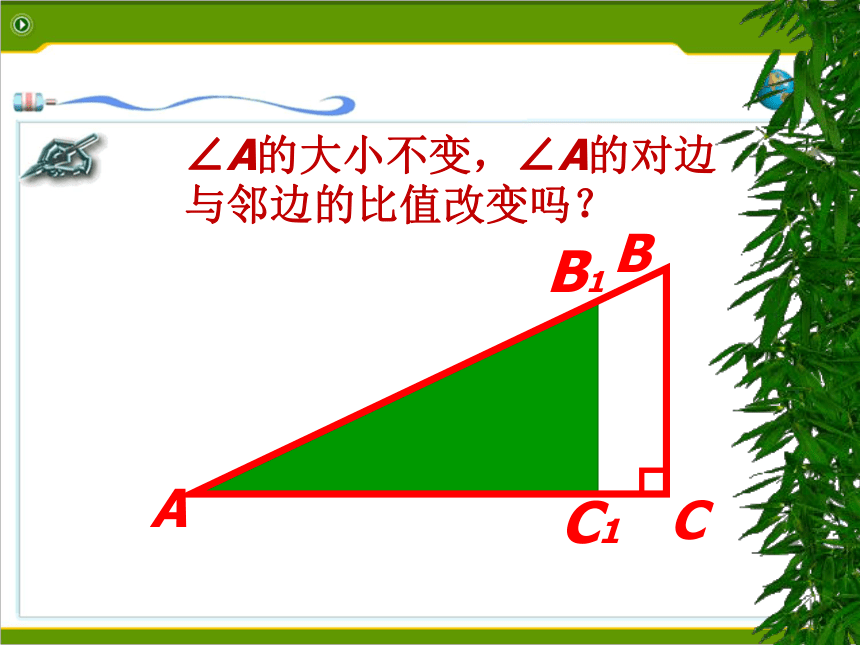
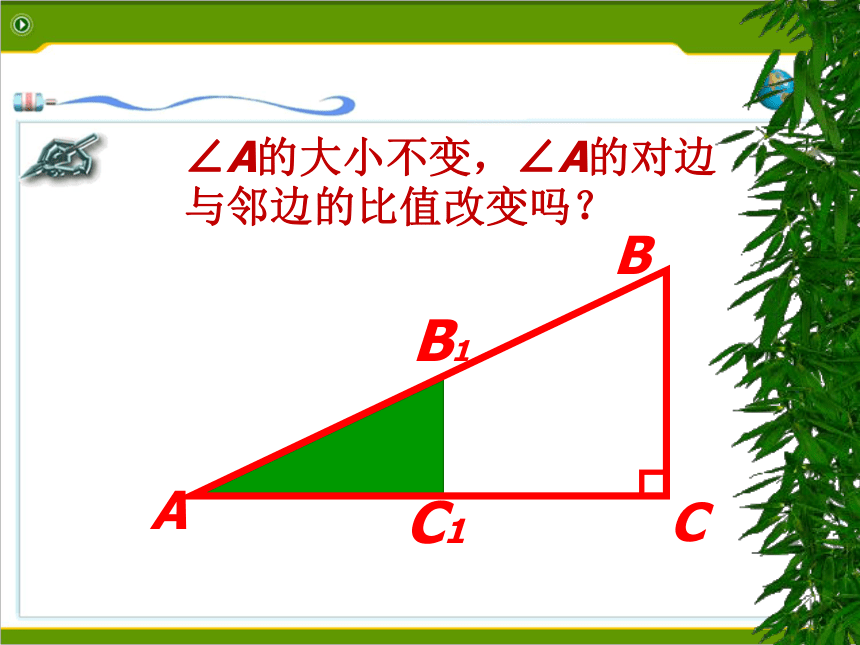
∠A的大小不变,∠A的对边与邻边的比值改变吗?
A
B
C
B1
C1
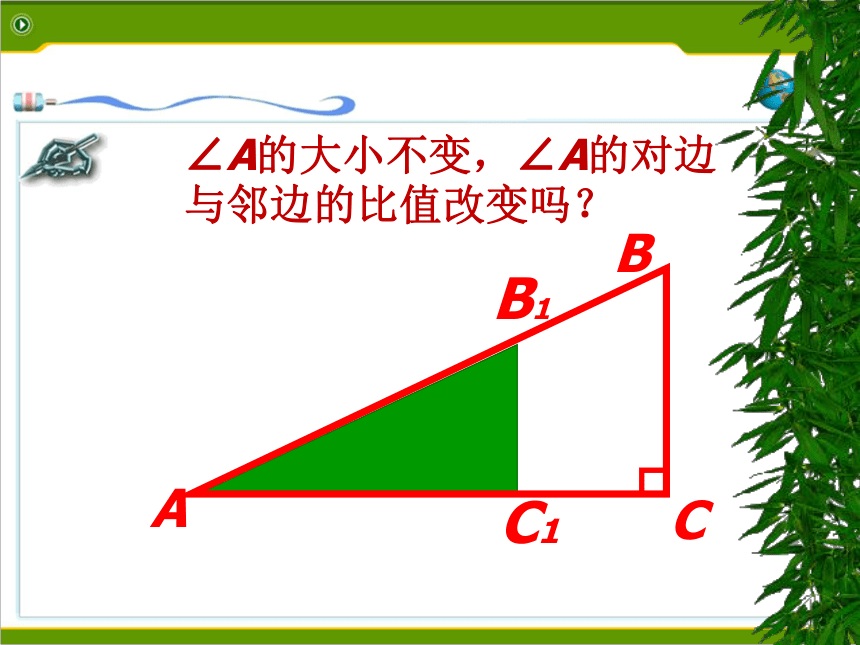
∠A的大小不变,∠A的对边与邻边的比值改变吗?
A
B
C
B1
C1
∠A的大小不变,∠A的对边与邻边的比值改变吗?
A
B
C
B1
C1
∠A的大小不变,∠A的对边与邻边的比值改变吗?
A
B
C
在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值。
定义:
在Rt△ABC中,我们把锐角A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即
tanA=
∠A的对边
∠A的邻边
注意:
1.
tanA是一个完整的符号,不表示tan乘以∠A。
2.∠A的正切表示为tanA
∠α的正切表示为tanα
∠BAC的正切要表示为tan∠BAC
∠1的正切表示为tan∠1
3.
tanA没有单位,它表示一个比值。
∠B的正切怎么表示?
∠A的邻边b
∠A的对边a
斜边c
新知引入
7
tanB=
∠B的对边
∠B的邻边
tanA
tanB=1
如何来描述坡面的坡度呢?
l
h
坡面的铅直高度h和水平长度l的比叫做坡面的坡度(或坡比)记作i,即
(坡度通常写成
的形式)
坡面与水平面的夹角叫做坡角(倾斜角),记作
于是有
新知引入
8
例1:如图,在Rt?ABC中,∠C=90°,AC=4,BC=3,
求tanA和tanB.
例题讲解
解:
9
例2.如图,某人从小山坡下的B点走了15米到达坡顶的A,已知点A到坡脚的垂直距离为9m,求坡的坡度.
例题讲解
A
B
C
解:根据题意可知:
直角三角形中AB=15,AC=9.
由勾股定理可得:BC=12
∴斜坡的坡度为3:4.
10
(1).tan
=
tan
=
(2).如图,∠ACB=90°CD⊥AB,
tan∠ACD=
tanB=
AC
B
A
应用新知
1.填空
11
tanA的大小只与∠A的大小有关,而与直角三角形的大小无关.
2.在Rt△ABC中,把它各边长度扩大为原来的20倍,tanA的值(
)
A.扩大为原来的20倍
B.缩小为原来的
C.不变
D.不能确定
C
学以致用
12
A
B
C
6
5
5
3
3
D
4
3.如图,求tanC=(
)
A.1
B.
C.
D.
C
在非直角三角形中求角的正切值,要作辅助线构造直角三角形来解决问题.
构造直角三角形
能力提升
14
1.谈谈本节课的收获.
2.你还有什么疑惑吗?
15
必做题:P114
练习
第2、3题.
布置作业
选做题:如图,△ABC是等腰直角三角形,∠C=90°.若AD是BC边上的角平分线,
求∠BAD的正切值.
16
正弦
sinA
“赛因A”
余弦
cosA
“抠赛因A”
正切
tanA
“谈进特A”
(1)若AC=9,AB=15,求tanA和tanB
AC=15
BC=20
tanA=
tanB=
在直角三角形中,已知任意两边的长度,可求两锐角的正切值.
在直角三角形中,已知任一边长度和一锐角正切值,可求另两边的长度.
A
B
C
(2).若AB=25,tanB=
,求AC和BC的长度.
3.在Rt△ABC中,∠C=90°
小试牛刀
13
沪科版九年级数学上册第二十三章
1
2
哪个轨道更陡?
你是如何判断的?
A
B
C
D
E
F
情境导入
3
探索新知
我们都有过走上坡路的经验,坡面有陡有平,在数学上该如何衡量坡面的倾斜程度呢?如图所示:
(二)
(一)
(1)
(1)
(2)
(2)
铅直高度
水平长度
4
如何判断如图两种斜坡,哪个更陡呢?
(1)
(2)
斜坡的铅直高度与水平长度的比越大,斜坡越陡。
5
思考交流
(1)
(2)
(一)
(二)
B1
C1
B2
C2
这些比例有什么关系?
=
=
△ABC∽△AB1C1
知识探究
6
B1
C1
∠A的大小不变,∠A的对边与邻边的比值改变吗?
A
B
C
B1
C1
∠A的大小不变,∠A的对边与邻边的比值改变吗?
A
B
C
B1
C1
∠A的大小不变,∠A的对边与邻边的比值改变吗?
A
B
C
B1
C1
∠A的大小不变,∠A的对边与邻边的比值改变吗?
A
B
C
在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与邻边的比是一个固定值。
定义:
在Rt△ABC中,我们把锐角A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即
tanA=
∠A的对边
∠A的邻边
注意:
1.
tanA是一个完整的符号,不表示tan乘以∠A。
2.∠A的正切表示为tanA
∠α的正切表示为tanα
∠BAC的正切要表示为tan∠BAC
∠1的正切表示为tan∠1
3.
tanA没有单位,它表示一个比值。
∠B的正切怎么表示?
∠A的邻边b
∠A的对边a
斜边c
新知引入
7
tanB=
∠B的对边
∠B的邻边
tanA
tanB=1
如何来描述坡面的坡度呢?
l
h
坡面的铅直高度h和水平长度l的比叫做坡面的坡度(或坡比)记作i,即
(坡度通常写成
的形式)
坡面与水平面的夹角叫做坡角(倾斜角),记作
于是有
新知引入
8
例1:如图,在Rt?ABC中,∠C=90°,AC=4,BC=3,
求tanA和tanB.
例题讲解
解:
9
例2.如图,某人从小山坡下的B点走了15米到达坡顶的A,已知点A到坡脚的垂直距离为9m,求坡的坡度.
例题讲解
A
B
C
解:根据题意可知:
直角三角形中AB=15,AC=9.
由勾股定理可得:BC=12
∴斜坡的坡度为3:4.
10
(1).tan
=
tan
=
(2).如图,∠ACB=90°CD⊥AB,
tan∠ACD=
tanB=
AC
B
A
应用新知
1.填空
11
tanA的大小只与∠A的大小有关,而与直角三角形的大小无关.
2.在Rt△ABC中,把它各边长度扩大为原来的20倍,tanA的值(
)
A.扩大为原来的20倍
B.缩小为原来的
C.不变
D.不能确定
C
学以致用
12
A
B
C
6
5
5
3
3
D
4
3.如图,求tanC=(
)
A.1
B.
C.
D.
C
在非直角三角形中求角的正切值,要作辅助线构造直角三角形来解决问题.
构造直角三角形
能力提升
14
1.谈谈本节课的收获.
2.你还有什么疑惑吗?
15
必做题:P114
练习
第2、3题.
布置作业
选做题:如图,△ABC是等腰直角三角形,∠C=90°.若AD是BC边上的角平分线,
求∠BAD的正切值.
16
正弦
sinA
“赛因A”
余弦
cosA
“抠赛因A”
正切
tanA
“谈进特A”
(1)若AC=9,AB=15,求tanA和tanB
AC=15
BC=20
tanA=
tanB=
在直角三角形中,已知任意两边的长度,可求两锐角的正切值.
在直角三角形中,已知任一边长度和一锐角正切值,可求另两边的长度.
A
B
C
(2).若AB=25,tanB=
,求AC和BC的长度.
3.在Rt△ABC中,∠C=90°
小试牛刀
13
