沪科版 九年级数学上册第23.2章解直角三角形及其应用课件(25张ppt)
文档属性
| 名称 | 沪科版 九年级数学上册第23.2章解直角三角形及其应用课件(25张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 987.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
2、如图,在Rt△ABC中,∠C=90°,
除了直角外,还有几个元素?
A
C
B
c
b
a
5个,两个锐角∠A
、∠B
、
三条边a、b、c
1、在三角形中共有几个基本元素?
6个,三个角,三条边
导入
引例
△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,你还能求出哪些未知元素呢?
A
B
C
a
b
c
3
30°
?
?
?
探究活动:
在直角三角形中除直角外至少需要已知几个元素就可以求出其余的元素呢?
观察思考
30°
30°
一个元素
一角
一边
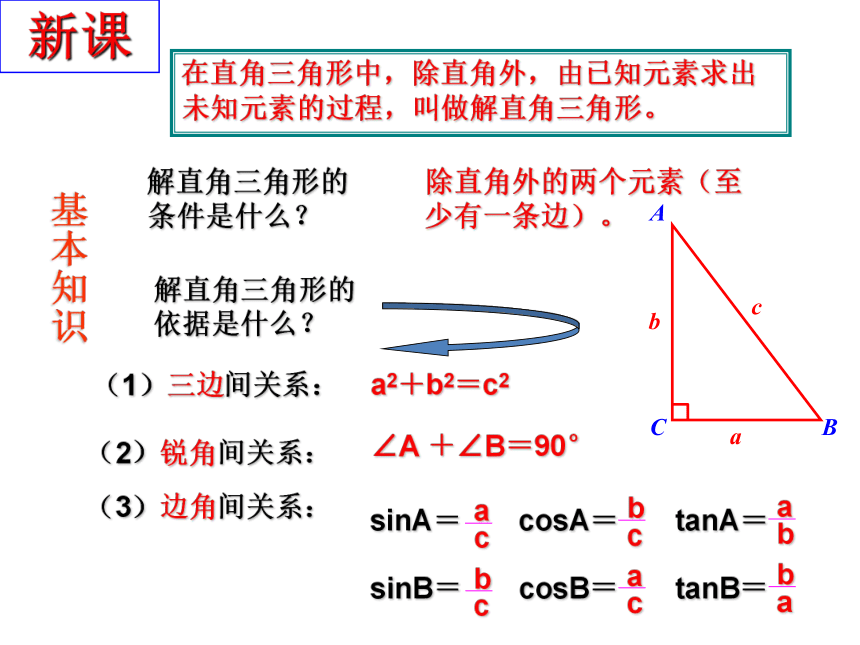
在Rt△ABC中,
(1)根据∠A=
60°,斜边AB=30,
A
在直角三角形的六个元素中,除直角外,如果知道两个元素,
就可以求出其余三个元素.
(其中至少有一个是边),
想
一
想
你发现了什么?
B
C
∠B
AC
BC
∠A
∠B
AB
一角一边
两边
(2)根据AC=
,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元
素吗?
不能
你能求出这个三角形的其他元素吗?
新课
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形。
解直角三角形的条件是什么?
解直角三角形的依据是什么?
除直角外的两个元素(至少有一条边)。
(1)三边间关系:
(2)锐角间关系:
(3)边角间关系:
a2+b2=c2
∠A
+∠B=90°
sinA= cosA= tanA=
a
c
b
c
a
b
sinB= cosB= tanB=
b
c
a
c
b
a
基本知识
A
B
a
b
c
C
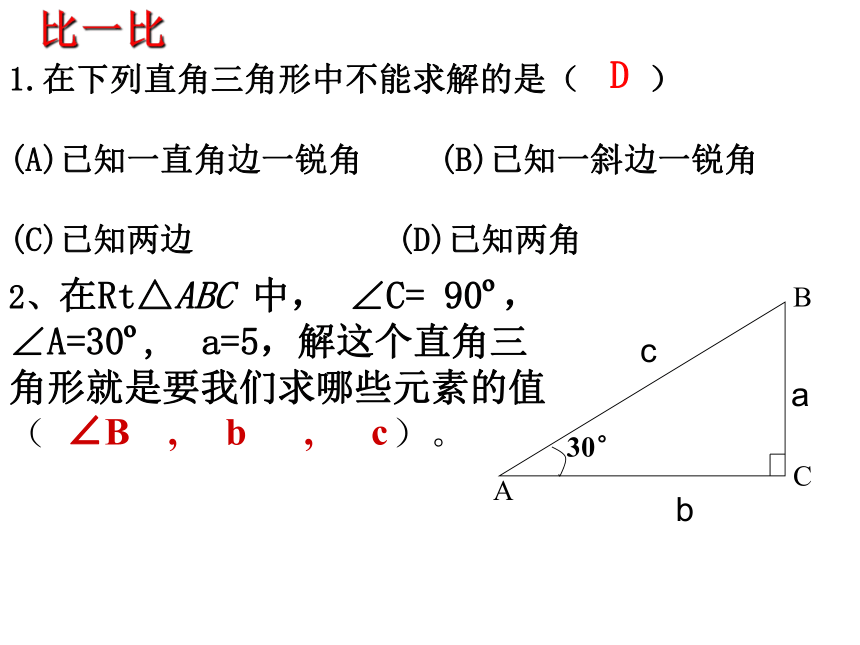
比一比
1.在下列直角三角形中不能求解的是(
)
(A)已知一直角边一锐角
(B)已知一斜边一锐角
(C)已知两边
(D)已知两角
D
2、在Rt△ABC
中,
∠C=
90?,∠A=30?,
a=5,解这个直角三角形就是要我们求哪些元素的值(
)。
∠B
,
b
,
c
A
B
C
30°
a
b
c
如图,在Rt△ABC中,∠C=90°
,
解这个直角三角形.
解:
A
B
C
例题讲解
例1、在Rt△ABC中,∠C=90°,∠B=42°6′,
c=287.4。解这个直角三角形(精确到0.1).
(cos42°6′=0.7420,
sin42°6′=0.6704)
解:如图
A
C
B
c
b
a
∠A
=90°
-
∠B
=
90°
-
42°6′=
47°54′
由cosB
=
得
a
=
c·cosB
=
287.4×0.7420≈213.3
由sinB
=
得
b=
c·sinB
=
287.4×0.6704≈192.7
例题拓展
例2、在△ABC中,∠A=550,b=20cm,c=30cm。求三角形的面积S△ABC
D
解:作AB边上的高CD
例题拓展
1、三角形的面积公式是什么?
2、本题已知什么?待求什么?
3、如何作高线,有几种方法?
是否每种方法都可行?
分析:
A
C
B
b
a
c
例2、在△ABC中,∠A=550,b=20cm,c=30cm。求三角形的面积S△ABC
(精确到0.1)
D
解:作AB边上的高CD,在Rt△ACD中
CD=AC·sinA=bsinA
当∠A=550,b=20cm,c=30cm时,有
例题拓展
△ABC的面积是否可以用a、c及夹角B或a、b及夹角C表示呢?
结论:
S
△ABC=
bc·sinA
=
ab·sinC
=
ac·sinB
A
C
B
b
a
c
例1:如图,在Rt△ABC中,∠C=90°,
∠B=30
°,
解这个直角三角形。
A
B
C
AB=8,
BC=4,
反思:
已知一边、一锐角
A
B
C
a
c
b
例2、如图:在Rt△ABC中,∠C=90°,BC=
,
AC=
解这个直角三角形。
B
A
C
已知
两边
反思:
A
B
C
a
c
b
小结方法:
解直角三角形选择公式时应遵循一个基本原则:
(2)有斜(斜边),用弦(正、余弦),无斜用切(正切),宁乘勿除,尽量采用原始数据。
(1)
有角先求角
无角先求边
解直角
三角形
∠A+
∠
B=90°
a2+b2=c2
三角函数
关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
归纳小结
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
通过本节课学习,我们有哪些收获?
方法小结:
通过本节课学习,我们学习了哪些内容?
1.利用直角三角形(除直角外)两个已知元素(至少有一个是边)去求其它元素。
2.解直角三角形的原则:
(1)
有角先求角
无角先求边
(2)
有斜用弦,
无斜用切;
宁乘勿除,
取原避中。
4.
本节课涉及到的解题的思想方法:
数形结合思想和转化思想.
3.三角面积的另一种计算公式
如图,在Rt△ABC中,∠C=90°
解这个直角三角形.
变式一
A
B
C
30°
BC还有其它求法吗?哪种求法更合适?
如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)
(参考数据:
)
变式二
A
B
C
a
b
c
20
35°
如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)
(参考数据:
)
解:∠A=90°-∠B=90°-35°=55°
A
B
C
a
b
c
20
35°
变式二
解直角三角形的原则:
有斜用弦,无斜用切,
宁乘勿除,取原避中。
练习
1、
△ABC中,
∠B=60°,
a=3cm,c=4cm。
则S
△ABC为多少?
2、平行四边形两邻边为4、6,夹角为30°,则其面
积为多少?
3、
△ABC中,
∠A=30°,
AB=4,AC=2
+2
。
求这个三角形的其它元素。
练习
在Rt△ABC
中,∠C=90°,根据下列条件解直角三角形;
(1)
a
=
30
,
b
=
20
(2)
∠B=72°,c
=
14
A
B
C
b=20
a=30
c
A
B
C
b
a
c=14
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a
=
30
,
b
=
20
;
练习
解:根据勾股定理
A
B
C
b=20
a=30
c
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(2)
∠B=72°,c
=
14.
A
B
C
b
a
c=14
解:
例3、在△ABC中,∠A=55°,b=20cm,c=30cm。求这个三角形的面积。(精确到0.1cm2)
A
C
B
b
a
c
2、三角形的面积公式是什么?
解:如图,作AB边上的高CD
在Rt△ACD中,CD=AC·sinA=b·sinA
∴S
△ABC=
AB·CD=
bc·sinA
当∠A=55°,b=20cm,c=30cm时,
∴S
△ABC=
bc·sinA
=
×20×30×sin
55°
=245.8(cm2)
=
×20×30×0.8192
1、本题已知什么?待求什么?
3、如何作高线,是否每种方法都可行?
△ABC的面积是否可以用a、c及夹角B或a、b及夹角C表示呢?
结论:
S
△ABC=
bc·sinA
=
ab·sinC
=
ac·sinB
D
方法小结:
1、利用直角三角形(除直角外)两个已知元素(至少有一个是边)去求其它元素。
4、三角形的另一种面积计算公式。
2、在遇到解直角三形的问题时,最好先画一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的.数形结合有利于分析解决问题。
3、解直角三角形的方法遵循“有斜用弦,无斜用切;
宁乘勿除,取原避中”的原则。
2、如图,在Rt△ABC中,∠C=90°,
除了直角外,还有几个元素?
A
C
B
c
b
a
5个,两个锐角∠A
、∠B
、
三条边a、b、c
1、在三角形中共有几个基本元素?
6个,三个角,三条边
导入
引例
△ABC中,∠C为直角,∠A,∠B,∠C所对的边分别为a,b,c,且b=3,∠A=30°,你还能求出哪些未知元素呢?
A
B
C
a
b
c
3
30°
?
?
?
探究活动:
在直角三角形中除直角外至少需要已知几个元素就可以求出其余的元素呢?
观察思考
30°
30°
一个元素
一角
一边
在Rt△ABC中,
(1)根据∠A=
60°,斜边AB=30,
A
在直角三角形的六个元素中,除直角外,如果知道两个元素,
就可以求出其余三个元素.
(其中至少有一个是边),
想
一
想
你发现了什么?
B
C
∠B
AC
BC
∠A
∠B
AB
一角一边
两边
(2)根据AC=
,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元
素吗?
不能
你能求出这个三角形的其他元素吗?
新课
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形。
解直角三角形的条件是什么?
解直角三角形的依据是什么?
除直角外的两个元素(至少有一条边)。
(1)三边间关系:
(2)锐角间关系:
(3)边角间关系:
a2+b2=c2
∠A
+∠B=90°
sinA= cosA= tanA=
a
c
b
c
a
b
sinB= cosB= tanB=
b
c
a
c
b
a
基本知识
A
B
a
b
c
C
比一比
1.在下列直角三角形中不能求解的是(
)
(A)已知一直角边一锐角
(B)已知一斜边一锐角
(C)已知两边
(D)已知两角
D
2、在Rt△ABC
中,
∠C=
90?,∠A=30?,
a=5,解这个直角三角形就是要我们求哪些元素的值(
)。
∠B
,
b
,
c
A
B
C
30°
a
b
c
如图,在Rt△ABC中,∠C=90°
,
解这个直角三角形.
解:
A
B
C
例题讲解
例1、在Rt△ABC中,∠C=90°,∠B=42°6′,
c=287.4。解这个直角三角形(精确到0.1).
(cos42°6′=0.7420,
sin42°6′=0.6704)
解:如图
A
C
B
c
b
a
∠A
=90°
-
∠B
=
90°
-
42°6′=
47°54′
由cosB
=
得
a
=
c·cosB
=
287.4×0.7420≈213.3
由sinB
=
得
b=
c·sinB
=
287.4×0.6704≈192.7
例题拓展
例2、在△ABC中,∠A=550,b=20cm,c=30cm。求三角形的面积S△ABC
D
解:作AB边上的高CD
例题拓展
1、三角形的面积公式是什么?
2、本题已知什么?待求什么?
3、如何作高线,有几种方法?
是否每种方法都可行?
分析:
A
C
B
b
a
c
例2、在△ABC中,∠A=550,b=20cm,c=30cm。求三角形的面积S△ABC
(精确到0.1)
D
解:作AB边上的高CD,在Rt△ACD中
CD=AC·sinA=bsinA
当∠A=550,b=20cm,c=30cm时,有
例题拓展
△ABC的面积是否可以用a、c及夹角B或a、b及夹角C表示呢?
结论:
S
△ABC=
bc·sinA
=
ab·sinC
=
ac·sinB
A
C
B
b
a
c
例1:如图,在Rt△ABC中,∠C=90°,
∠B=30
°,
解这个直角三角形。
A
B
C
AB=8,
BC=4,
反思:
已知一边、一锐角
A
B
C
a
c
b
例2、如图:在Rt△ABC中,∠C=90°,BC=
,
AC=
解这个直角三角形。
B
A
C
已知
两边
反思:
A
B
C
a
c
b
小结方法:
解直角三角形选择公式时应遵循一个基本原则:
(2)有斜(斜边),用弦(正、余弦),无斜用切(正切),宁乘勿除,尽量采用原始数据。
(1)
有角先求角
无角先求边
解直角
三角形
∠A+
∠
B=90°
a2+b2=c2
三角函数
关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
归纳小结
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
通过本节课学习,我们有哪些收获?
方法小结:
通过本节课学习,我们学习了哪些内容?
1.利用直角三角形(除直角外)两个已知元素(至少有一个是边)去求其它元素。
2.解直角三角形的原则:
(1)
有角先求角
无角先求边
(2)
有斜用弦,
无斜用切;
宁乘勿除,
取原避中。
4.
本节课涉及到的解题的思想方法:
数形结合思想和转化思想.
3.三角面积的另一种计算公式
如图,在Rt△ABC中,∠C=90°
解这个直角三角形.
变式一
A
B
C
30°
BC还有其它求法吗?哪种求法更合适?
如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)
(参考数据:
)
变式二
A
B
C
a
b
c
20
35°
如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)
(参考数据:
)
解:∠A=90°-∠B=90°-35°=55°
A
B
C
a
b
c
20
35°
变式二
解直角三角形的原则:
有斜用弦,无斜用切,
宁乘勿除,取原避中。
练习
1、
△ABC中,
∠B=60°,
a=3cm,c=4cm。
则S
△ABC为多少?
2、平行四边形两邻边为4、6,夹角为30°,则其面
积为多少?
3、
△ABC中,
∠A=30°,
AB=4,AC=2
+2
。
求这个三角形的其它元素。
练习
在Rt△ABC
中,∠C=90°,根据下列条件解直角三角形;
(1)
a
=
30
,
b
=
20
(2)
∠B=72°,c
=
14
A
B
C
b=20
a=30
c
A
B
C
b
a
c=14
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a
=
30
,
b
=
20
;
练习
解:根据勾股定理
A
B
C
b=20
a=30
c
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(2)
∠B=72°,c
=
14.
A
B
C
b
a
c=14
解:
例3、在△ABC中,∠A=55°,b=20cm,c=30cm。求这个三角形的面积。(精确到0.1cm2)
A
C
B
b
a
c
2、三角形的面积公式是什么?
解:如图,作AB边上的高CD
在Rt△ACD中,CD=AC·sinA=b·sinA
∴S
△ABC=
AB·CD=
bc·sinA
当∠A=55°,b=20cm,c=30cm时,
∴S
△ABC=
bc·sinA
=
×20×30×sin
55°
=245.8(cm2)
=
×20×30×0.8192
1、本题已知什么?待求什么?
3、如何作高线,是否每种方法都可行?
△ABC的面积是否可以用a、c及夹角B或a、b及夹角C表示呢?
结论:
S
△ABC=
bc·sinA
=
ab·sinC
=
ac·sinB
D
方法小结:
1、利用直角三角形(除直角外)两个已知元素(至少有一个是边)去求其它元素。
4、三角形的另一种面积计算公式。
2、在遇到解直角三形的问题时,最好先画一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的.数形结合有利于分析解决问题。
3、解直角三角形的方法遵循“有斜用弦,无斜用切;
宁乘勿除,取原避中”的原则。
