沪科版九年级数学上册第23章解直角三角形复习课件(22张ppt)
文档属性
| 名称 | 沪科版九年级数学上册第23章解直角三角形复习课件(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
1
2
考
试
内
容
考试要求目标
单
元
知
识
条
目
A
B
C
D
图
形
的
变
化
锐角三角函数的意义
?
√
?
?
30°、45°、60°角的三角函数值
?
√
?
?
解直角三角形及其简单的实际问题
?
?
√
?
A:了解
B:理解
C:掌握
D:运用
中考考纲要求
三边之间的关系:
锐角之间的关系:
边角之间的关系:
A
B
b
a
c
┏
C
解直角三角形的依据
正切值随着锐角的度数的增大而_____;
正弦值随着锐角的度数的增大而_____;
余弦值随着锐角的度数的增大而_____.
增大
增大
减小
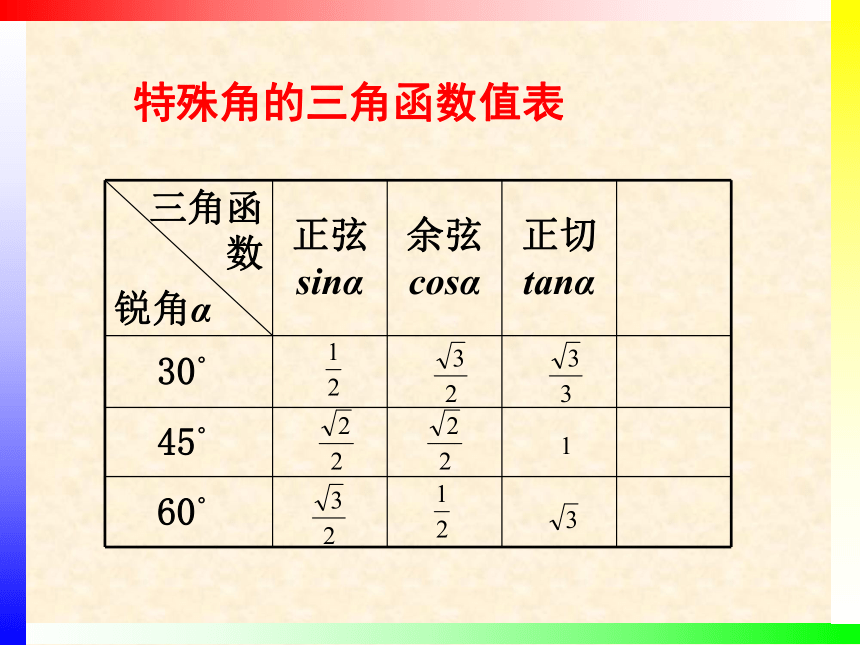
特殊角的三角函数值表
三角函数
锐角α
正弦sinα
余弦cosα
正切tanα
30°
45°
60°
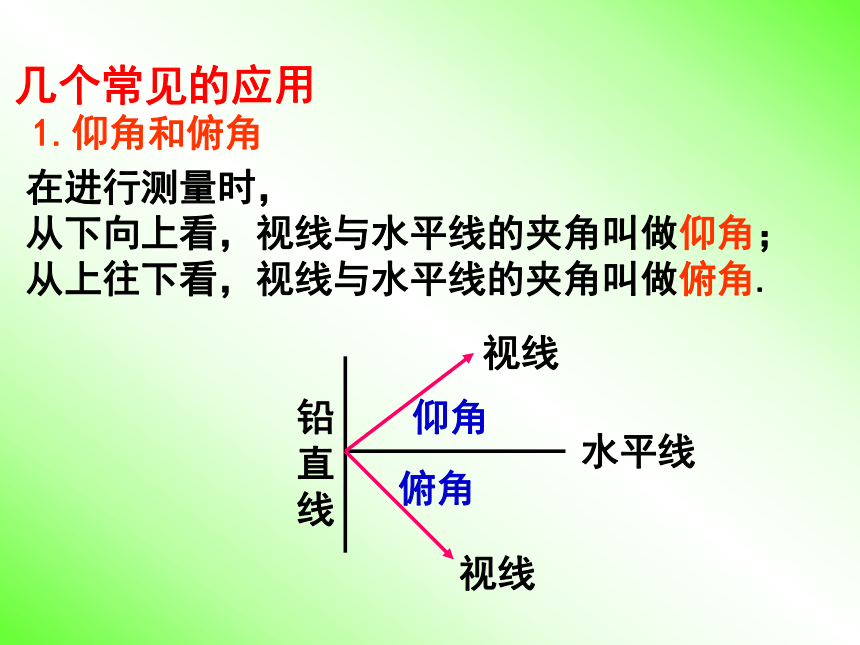
1.仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
几个常见的应用
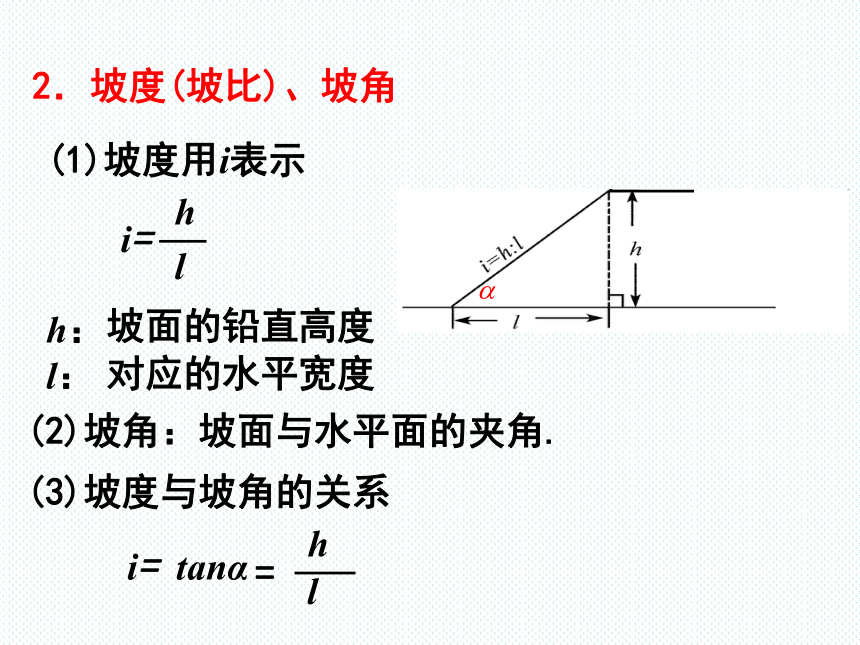
2.坡度(坡比)、坡角
(3)坡度与坡角的关系
(1)坡度用i表示
i=
h:
l:
(2)坡角:坡面与水平面的夹角.
i=
tanα
=
h
l
h
l
坡面的铅直高度
对应的水平宽度
8
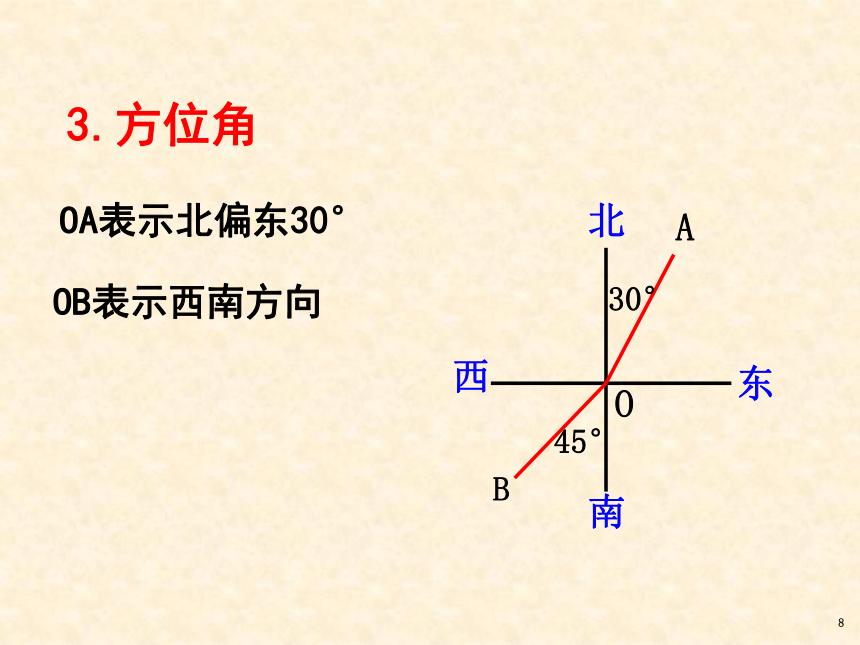
3.方位角
30°
45°
B
O
A
东
西
北
南
OA表示北偏东30°
OB表示西南方向
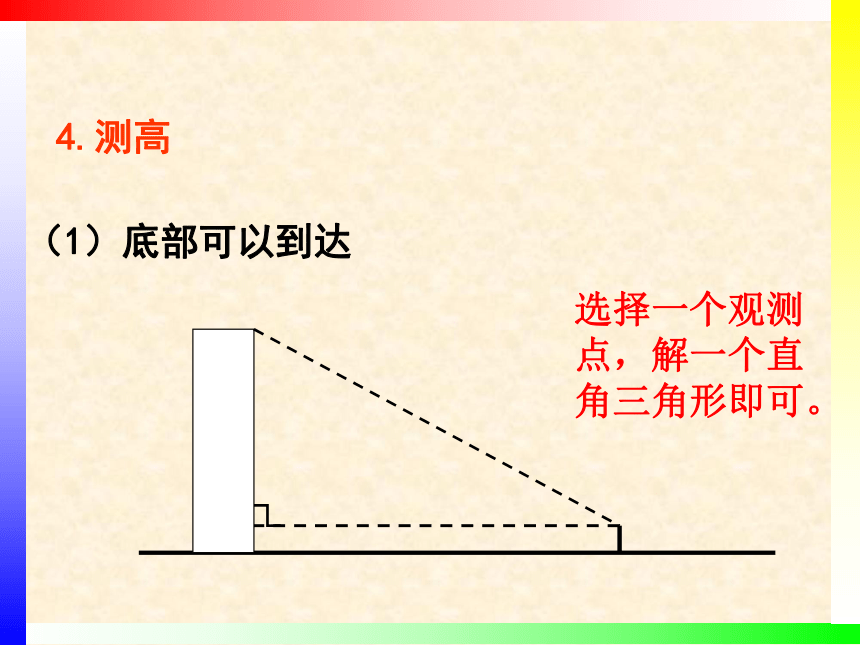
4.测高
(1)底部可以到达
选择一个观测点,解一个直角三角形即可。
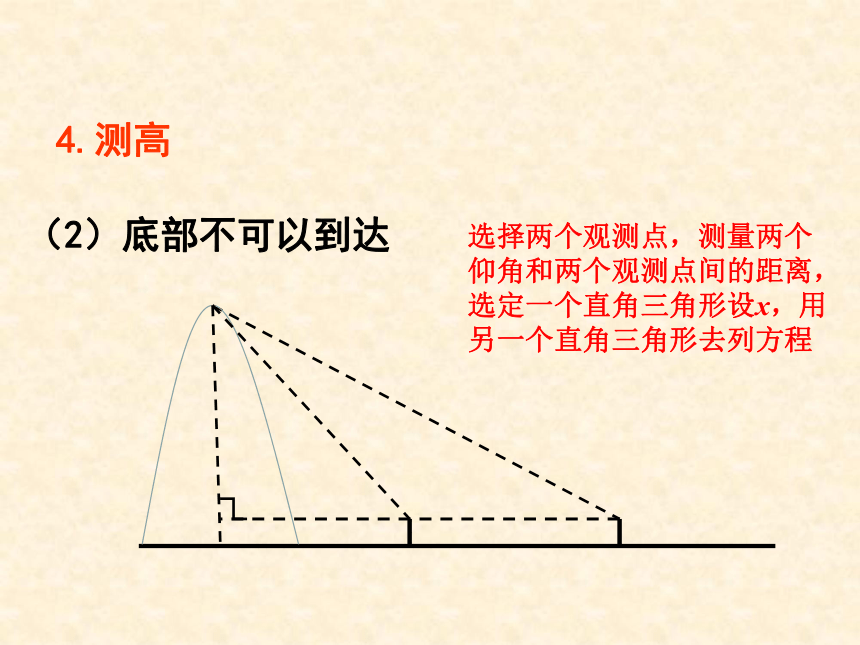
4.测高
(2)底部不可以到达
选择两个观测点,测量两个仰角和两个观测点间的距离,选定一个直角三角形设x,用另一个直角三角形去列方程
模型1
如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
模型2
如图,根据图中已知数据,求AD.
A
B
C
β
α
a
D
┌
A
B
C
α
β
a
两种模型
转化思想和方程思想
模型一:
30。
30。
30。
30。
60。
60。
45。
45。
a
a
a
a
转化思想
模型二:
45。
30。
60。
45。
60。
30。
a
提示:
1、利用45。角的直角三角形去设;
2、利用30。角的直角三角形列方程。
两个30。角的直角三角形组合
1、有可能出现等腰三角形;
2、如果用方程做,一般设较小的直角三角形的较短直角边为x
。
四个解直角三角形的典型变式图形
【化斜为直】,【善于转化】
2017年15题:
2016年15题:
2013年15题:
近几年安徽中考真题
2013年第19题:如图,防洪大堤的横截面是梯形ABCD,其中AD∥BC,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°.若原坡长AB=20m,求改造后的坡长AE.(结果保留根号)
F
2014年第18题:如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
E
F
G
2016年第19题:如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
∵DF⊥AF,
∴∠DFB=90°,
∴AC∥DF,
由已知l1∥l2,
∴CD∥AF,
∴四边形ACDF为矩形,CD=AF=AE+EF=30,
答:C、D两点间的距离为30m.
∵四边形BCEF是矩形,
∴EF=BC=156,
∴DE=DF+EF=423+156=579m.
答:DE的长为579m.
方法小结:
1.把实际问题转化成数学问题,这个转化为两个方面:
一是将实际问题的图形转化为几何图形,画出正确的平面或截面示意图.
二是将已知条件转化为示意图中的边、角或它们之间的关系.
2.把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形.
完成综合练习册相关内容
课后作业
独立完成作业的良好习惯,是成长过程中的良师益友。
1
2
考
试
内
容
考试要求目标
单
元
知
识
条
目
A
B
C
D
图
形
的
变
化
锐角三角函数的意义
?
√
?
?
30°、45°、60°角的三角函数值
?
√
?
?
解直角三角形及其简单的实际问题
?
?
√
?
A:了解
B:理解
C:掌握
D:运用
中考考纲要求
三边之间的关系:
锐角之间的关系:
边角之间的关系:
A
B
b
a
c
┏
C
解直角三角形的依据
正切值随着锐角的度数的增大而_____;
正弦值随着锐角的度数的增大而_____;
余弦值随着锐角的度数的增大而_____.
增大
增大
减小
特殊角的三角函数值表
三角函数
锐角α
正弦sinα
余弦cosα
正切tanα
30°
45°
60°
1.仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
几个常见的应用
2.坡度(坡比)、坡角
(3)坡度与坡角的关系
(1)坡度用i表示
i=
h:
l:
(2)坡角:坡面与水平面的夹角.
i=
tanα
=
h
l
h
l
坡面的铅直高度
对应的水平宽度
8
3.方位角
30°
45°
B
O
A
东
西
北
南
OA表示北偏东30°
OB表示西南方向
4.测高
(1)底部可以到达
选择一个观测点,解一个直角三角形即可。
4.测高
(2)底部不可以到达
选择两个观测点,测量两个仰角和两个观测点间的距离,选定一个直角三角形设x,用另一个直角三角形去列方程
模型1
如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
模型2
如图,根据图中已知数据,求AD.
A
B
C
β
α
a
D
┌
A
B
C
α
β
a
两种模型
转化思想和方程思想
模型一:
30。
30。
30。
30。
60。
60。
45。
45。
a
a
a
a
转化思想
模型二:
45。
30。
60。
45。
60。
30。
a
提示:
1、利用45。角的直角三角形去设;
2、利用30。角的直角三角形列方程。
两个30。角的直角三角形组合
1、有可能出现等腰三角形;
2、如果用方程做,一般设较小的直角三角形的较短直角边为x
。
四个解直角三角形的典型变式图形
【化斜为直】,【善于转化】
2017年15题:
2016年15题:
2013年15题:
近几年安徽中考真题
2013年第19题:如图,防洪大堤的横截面是梯形ABCD,其中AD∥BC,α=60°,汛期来临前对其进行了加固,改造后的背水面坡角β=45°.若原坡长AB=20m,求改造后的坡长AE.(结果保留根号)
F
2014年第18题:如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
E
F
G
2016年第19题:如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
∵DF⊥AF,
∴∠DFB=90°,
∴AC∥DF,
由已知l1∥l2,
∴CD∥AF,
∴四边形ACDF为矩形,CD=AF=AE+EF=30,
答:C、D两点间的距离为30m.
∵四边形BCEF是矩形,
∴EF=BC=156,
∴DE=DF+EF=423+156=579m.
答:DE的长为579m.
方法小结:
1.把实际问题转化成数学问题,这个转化为两个方面:
一是将实际问题的图形转化为几何图形,画出正确的平面或截面示意图.
二是将已知条件转化为示意图中的边、角或它们之间的关系.
2.把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形.
完成综合练习册相关内容
课后作业
独立完成作业的良好习惯,是成长过程中的良师益友。
