2020-2021学年人教版八年级下册同步练习:19.1.2 函数图象表示方法及其画法(Word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册同步练习:19.1.2 函数图象表示方法及其画法(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 558.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 18:05:51 | ||
图片预览




文档简介
19.1.2
函数图象表示方法及其画法
命题点
1 函数图象及其画法
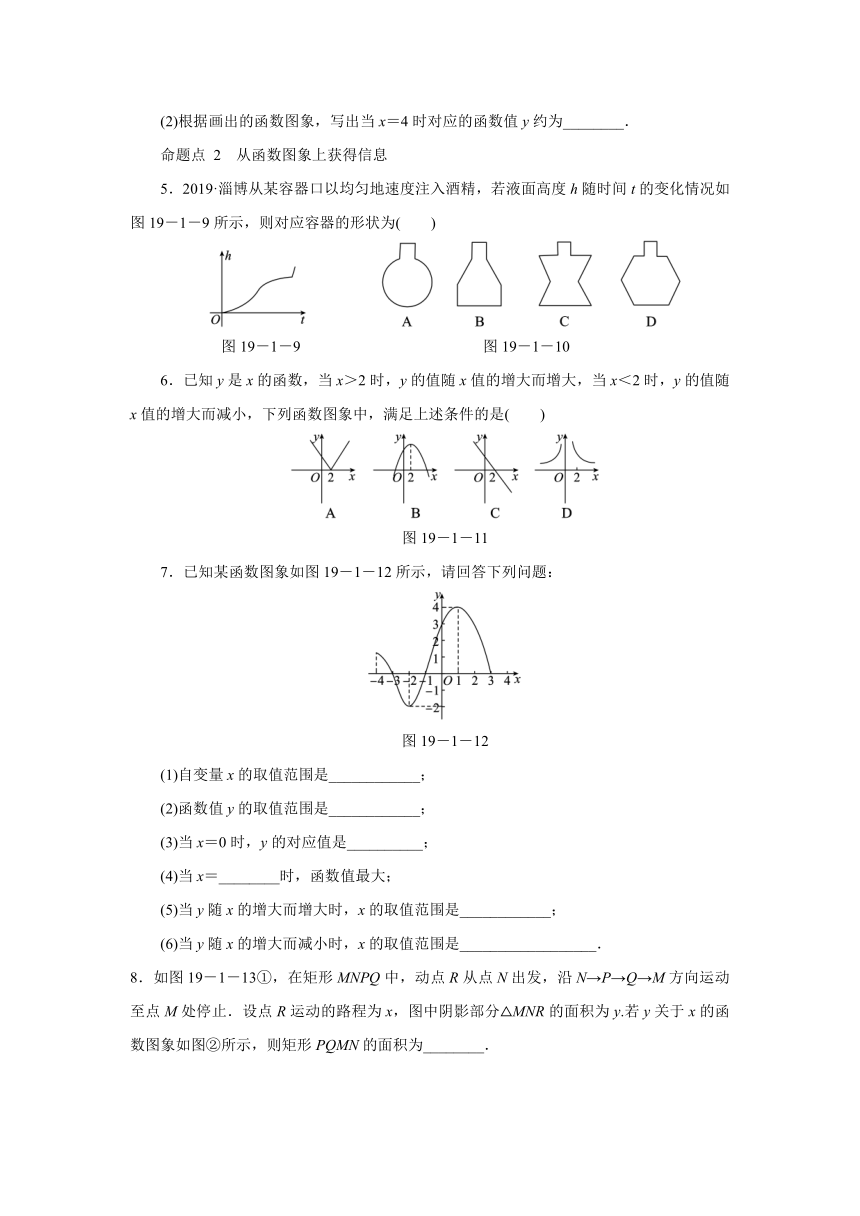
1.下列曲线中不能表示y是x的函数的是( )
图19-1-6
2.下列各点中,不在函数y=的图象上的是( )
A.(2,)
B.(1,1)
C.(-1,)
D.(0,-1)
3.函数y=+x的图象是( )
图19-1-7
4.已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值:
x
…
1
2
3
5
7
9
…
y
…
1.98
3.95
2.63
1.58
1.13
0.88
…
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图19-1-8,在平面直角坐标系xOy中,描出了以上面表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
图19-1-8
(2)根据画出的函数图象,写出当x=4时对应的函数值y约为________.
命题点
2 从函数图象上获得信息
5.2019·淄博从某容器口以均匀地速度注入酒精,若液面高度h随时间t的变化情况如图19-1-9所示,则对应容器的形状为( )
图19-1-9
图19-1-10
6.已知y是x的函数,当x>2时,y的值随x值的增大而增大,当x<2时,y的值随x值的增大而减小,下列函数图象中,满足上述条件的是( )
图19-1-11
7.已知某函数图象如图19-1-12所示,请回答下列问题:
图19-1-12
(1)自变量x的取值范围是____________;
(2)函数值y的取值范围是____________;
(3)当x=0时,y的对应值是__________;
(4)当x=________时,函数值最大;
(5)当y随x的增大而增大时,x的取值范围是____________;
(6)当y随x的增大而减小时,x的取值范围是__________________.
8.如图19-1-13①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,图中阴影部分△MNR的面积为y.若y关于x的函数图象如图②所示,则矩形PQMN的面积为________.
图19-1-13
9.某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分)之间的关系如图19-1-14所示,根据图象解答下列问题:
(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(2)洗衣机清洗衣服所用的时间是多少分钟?
图19-1-14
10.小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图19-1-15反映了他们两人离开学校的路程s(千米)与时间t(分)的关系,请根据图象提供的信息回答下列问题:
(1)l1和l2哪一条描述的是小凡的运动过程?说明你的理由;
(2)小凡和小光谁先出发,先出发了多少分钟?
(3)小凡与小光谁先到达图书馆,先到了多少分钟?
(4)小凡与小光从学校到图书馆的平均速度各是多少千米/时?(不包括中间停留的时间)
图19-1-15
命题点3 图象法、列表法、解析式法表示函数的综合应用
11.温度计有华氏、摄氏两种温标,华氏(℉)、摄氏(℃)温标的转换公式是F=1.8C+32,请填写下表:
华氏(℉)
摄氏(℃)
温度描述
212
水沸腾的温度
37
人体温度
68
舒适室温
0
水结冰的温度
12.某商场经营一批小商品,在经营中发现此商品的日销售单价与日销量之间的关系如下表:
日销售单价(元/件)
3
5
7
9
11
日销量(件)
18
14
10
6
2
如果用x表示日销售单价,y表示日销量,请求出y与x之间的关系式.(不需要写出自变量的取值范围)
13.如图19-1-17,在边长为12
cm的正方形的四个角上分别剪去一个形状和大小均相同的等腰直角三角形,当三角形的直角边长由小变大时,阴影部分的面积也随之发生变化.
三角形的
直角边长(cm)
1
2
3
4
5
6
阴影部分
的面积(cm2)
142
____
126
112
____
72
(1)将表中的数据补充完整;
(2)当等腰直角三角形的直角边长由1
cm增加到6
cm时,阴影部分的面积怎样变化?
(3)设等腰直角三角形的直角边长为a
cm,图中阴影部分的面积为S
cm2,写出S与a之间的关系式(不需要写出自变量的取值范围).
图19-1-17
14.八年级(2)班同学为了探索泥茶壶盛水喝起来凉的原因,对泥茶壶和塑料壶盛水散热情况进行对比试验.在同等情况下,把高于室温(25.5
℃)的水倒入两壶中,每隔一小时同时测量两壶水温,所得数据如下表:
时间t(h)
温度
y(℃)
名称
刚倒
入时
1
2
3
4
5
6
7
泥茶壶
34
27
25
23.5
23.0
22.5
22.5
22.5
塑料壶
34
30
27
26.0
25.5
25.5
25.5
25.5
(1)塑料壶水温变化曲线如图19-1-18,请在同一平面直角坐标系中,画出泥茶壶水温的变化曲线;
(2)写出泥茶壶和塑料壶中水温变化情况的不同点.
图19-1-18
15.某同学根据图19-1-19①所示的程序计算后,画出了图②中y与x之间的函数图象.
(1)当0≤x≤3时,y与x之间的函数解析式为__________;
(2)当x>3时,求出y与x之间的函数解析式.
图19-1-19
16.如图19-1-20①,在长方形ABCD中,AB=10
cm,BC=8
cm,点P从点A出发,沿A→B→C→D的路线运动,到点D时停止运动.点P开始运动时的速度为1
cm/s,a
s后变为b
cm/s,图②是点P出发x
s后,△APD的面积S(cm2)与x(s)之间的函数关系图象.
(1)当点P在AB边上运动时,△APD的面积________,当点P在BC边上运动时,△APD的面积________,当点P在CD边上运动时,△APD的面积________;(填“逐渐增大”“逐渐减小”或“不变”)
(2)根据图②中提供的信息,求a,b及图②中c的值;
(3)设点P离开点A的路程为y(cm),请写出动点P改变速度后y与运动时间x(s)之间的函数关系式.
图19-1-20
17.一游泳池长90米,甲、乙两人分别从两对边同时向所对的另一边游去,到达对边后,再返回,这样往复数次.图19-1-16中的实线和虚线分别表示甲、乙与游泳池固定一边的距离随游泳时间变化的情况,请根据图象回答:
(1)甲、乙两人分别游了几个来回?
(2)甲、乙两人在整个游泳过程中,谁曾休息过?休息了几次?
(3)甲游了多长时间?游泳的速度是多少?
(4)在整个游泳过程中,甲、乙两人相遇了几次?
图19-1-16
18.2020·秦皇岛海港模拟如图19-1-21①,某容器由A,B,C三个长方体组成,其中A,B,C的底面积分别为25
cm2,10
cm2,5
cm2,C的容积是该容器容积的(容器各面的厚度忽略不计).现以速度v(单位:
cm3/s)均匀地向容器内注水,直至注满为止.图②是注水全过程中容器的水面高度h(单位:
cm)与注水时间t(单位:s)之间的函数图象.
(1)在注水过程中,注满A所用时间为________s,再注满B又用了________s;
(2)求A的高度及注水的速度v;
(3)求注满容器所需时间及容器的高度.
图19-1-21
典题讲评与答案详析
1.C 2.C
3.C [解析]
因为x≠0,所以可排除A,B.因为当x=-1时,y=-2,所以可排除D.
4.解:(1)如图.
(2)1.98(答案合理即可)
5.C
6.A [解析]
过点(2,0)作一条垂直于x轴的直线x=2,当x>2时,y的值随x值的增大而增大,说明图象在直线x=2的右侧是上升的,当x<2时,y的值随x值的增大而减小,说明图象在直线x=2的左侧是下降的.
7.(1)-4≤x≤3 (2)-2≤y≤4
(3)3 (4)1
(5)-2≤x≤1
(6)-4≤x≤-2或1≤x≤3
8.20
9.解:(1)洗衣机的进水时间是4分钟,清洗时洗衣机中的水量是40升.
(2)由图象可知,洗衣机清洗衣服所用的时间是15-4=11(分).
10.解:(1)l1描述的是小凡的运动过程.理由:
因为小凡在路边超市买了一些学习用品,需要停留一段时间,此时间段内小凡距学校的路程没有变化,所以l1描述的是小凡的运动过程.
(2)观察两函数图象,发现:小凡先出发,比小光先出发了10分钟.
(3)60-50=10(分),所以小光先到达图书馆,比小凡先到了10分钟.
(4)小凡的平均速度为5÷=10(千米/时),小光的平均速度为5÷=7.5(千米/时).
答:小凡从学校到图书馆的平均速度是10千米/时,小光从学校到图书馆的平均速度是7.5千米/时.
11.表中从上到下依次填:100 98.6 20 32
12.解:根据表格能看出当日销售单价每增加1元/件时,日销售量减少2件,
因此y=18-2(x-3)=-2x+24,即y=-2x+24.
13.解:(1)136 94
(2)当等腰直角三角形的直角边长由1
cm增加到6
cm时,阴影部分的面积由142
cm2逐渐减小到72
cm2.
(3)S=122-4××a2=-2a2+144.
14.解:(1)如图.
(2)泥茶壶中水温开始时下降幅度比塑料壶中水温下降幅度大.当两壶中水温基本稳定后,泥茶壶中的水温低于室温,而塑料壶中水温等于室温.
15.解:(1)y=5x+3
(2)当x>3时,根据题意,得y=(x-7)2+m.
把(10,11)代入,得9+m=11,解得m=2,
所以当x>3时,y与x之间的函数解析式为y=(x-7)2+2.
16.解:(1)逐渐增大 不变 逐渐减小
(2)当点P与点B重合时,S=×8×10=40(cm2).
由图象可知,当x=a时,S=24,即此时点P在边AB上,
所以S=×8×AP=24,
解得AP=6
cm,
所以a=6,此时BP=4
cm.
当x=8时,S=40,
所以8-a=2,
则b==2.
c=8+=17.
(3)y=6+2(x-6)=2x-6(6≤x≤17).
17.解:(1)甲游了3个来回,乙游了2个来回.
(2)乙曾休息过,休息了两次.
(3)甲游了180秒,游泳的速度是90×6÷180=3(米/秒).
(4)甲、乙两人相遇了5次.
18.解:(1)10 8
(2)设A的高度为a
cm,列方程组为解得
答:A的高度为4
cm,注水的速度v为10
cm3/s.
(3)18÷1-=18÷=24(s).
则10×(24-18)=5×hc,解得hc=12.
∴容器的高度为12+12=24(cm).
答:注满容器所需时间为24
s,容器的高度为24
cm.
函数图象表示方法及其画法
命题点
1 函数图象及其画法
1.下列曲线中不能表示y是x的函数的是( )
图19-1-6
2.下列各点中,不在函数y=的图象上的是( )
A.(2,)
B.(1,1)
C.(-1,)
D.(0,-1)
3.函数y=+x的图象是( )
图19-1-7
4.已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值:
x
…
1
2
3
5
7
9
…
y
…
1.98
3.95
2.63
1.58
1.13
0.88
…
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图19-1-8,在平面直角坐标系xOy中,描出了以上面表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
图19-1-8
(2)根据画出的函数图象,写出当x=4时对应的函数值y约为________.
命题点
2 从函数图象上获得信息
5.2019·淄博从某容器口以均匀地速度注入酒精,若液面高度h随时间t的变化情况如图19-1-9所示,则对应容器的形状为( )
图19-1-9
图19-1-10
6.已知y是x的函数,当x>2时,y的值随x值的增大而增大,当x<2时,y的值随x值的增大而减小,下列函数图象中,满足上述条件的是( )
图19-1-11
7.已知某函数图象如图19-1-12所示,请回答下列问题:
图19-1-12
(1)自变量x的取值范围是____________;
(2)函数值y的取值范围是____________;
(3)当x=0时,y的对应值是__________;
(4)当x=________时,函数值最大;
(5)当y随x的增大而增大时,x的取值范围是____________;
(6)当y随x的增大而减小时,x的取值范围是__________________.
8.如图19-1-13①,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,图中阴影部分△MNR的面积为y.若y关于x的函数图象如图②所示,则矩形PQMN的面积为________.
图19-1-13
9.某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分)之间的关系如图19-1-14所示,根据图象解答下列问题:
(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(2)洗衣机清洗衣服所用的时间是多少分钟?
图19-1-14
10.小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图19-1-15反映了他们两人离开学校的路程s(千米)与时间t(分)的关系,请根据图象提供的信息回答下列问题:
(1)l1和l2哪一条描述的是小凡的运动过程?说明你的理由;
(2)小凡和小光谁先出发,先出发了多少分钟?
(3)小凡与小光谁先到达图书馆,先到了多少分钟?
(4)小凡与小光从学校到图书馆的平均速度各是多少千米/时?(不包括中间停留的时间)
图19-1-15
命题点3 图象法、列表法、解析式法表示函数的综合应用
11.温度计有华氏、摄氏两种温标,华氏(℉)、摄氏(℃)温标的转换公式是F=1.8C+32,请填写下表:
华氏(℉)
摄氏(℃)
温度描述
212
水沸腾的温度
37
人体温度
68
舒适室温
0
水结冰的温度
12.某商场经营一批小商品,在经营中发现此商品的日销售单价与日销量之间的关系如下表:
日销售单价(元/件)
3
5
7
9
11
日销量(件)
18
14
10
6
2
如果用x表示日销售单价,y表示日销量,请求出y与x之间的关系式.(不需要写出自变量的取值范围)
13.如图19-1-17,在边长为12
cm的正方形的四个角上分别剪去一个形状和大小均相同的等腰直角三角形,当三角形的直角边长由小变大时,阴影部分的面积也随之发生变化.
三角形的
直角边长(cm)
1
2
3
4
5
6
阴影部分
的面积(cm2)
142
____
126
112
____
72
(1)将表中的数据补充完整;
(2)当等腰直角三角形的直角边长由1
cm增加到6
cm时,阴影部分的面积怎样变化?
(3)设等腰直角三角形的直角边长为a
cm,图中阴影部分的面积为S
cm2,写出S与a之间的关系式(不需要写出自变量的取值范围).
图19-1-17
14.八年级(2)班同学为了探索泥茶壶盛水喝起来凉的原因,对泥茶壶和塑料壶盛水散热情况进行对比试验.在同等情况下,把高于室温(25.5
℃)的水倒入两壶中,每隔一小时同时测量两壶水温,所得数据如下表:
时间t(h)
温度
y(℃)
名称
刚倒
入时
1
2
3
4
5
6
7
泥茶壶
34
27
25
23.5
23.0
22.5
22.5
22.5
塑料壶
34
30
27
26.0
25.5
25.5
25.5
25.5
(1)塑料壶水温变化曲线如图19-1-18,请在同一平面直角坐标系中,画出泥茶壶水温的变化曲线;
(2)写出泥茶壶和塑料壶中水温变化情况的不同点.
图19-1-18
15.某同学根据图19-1-19①所示的程序计算后,画出了图②中y与x之间的函数图象.
(1)当0≤x≤3时,y与x之间的函数解析式为__________;
(2)当x>3时,求出y与x之间的函数解析式.
图19-1-19
16.如图19-1-20①,在长方形ABCD中,AB=10
cm,BC=8
cm,点P从点A出发,沿A→B→C→D的路线运动,到点D时停止运动.点P开始运动时的速度为1
cm/s,a
s后变为b
cm/s,图②是点P出发x
s后,△APD的面积S(cm2)与x(s)之间的函数关系图象.
(1)当点P在AB边上运动时,△APD的面积________,当点P在BC边上运动时,△APD的面积________,当点P在CD边上运动时,△APD的面积________;(填“逐渐增大”“逐渐减小”或“不变”)
(2)根据图②中提供的信息,求a,b及图②中c的值;
(3)设点P离开点A的路程为y(cm),请写出动点P改变速度后y与运动时间x(s)之间的函数关系式.
图19-1-20
17.一游泳池长90米,甲、乙两人分别从两对边同时向所对的另一边游去,到达对边后,再返回,这样往复数次.图19-1-16中的实线和虚线分别表示甲、乙与游泳池固定一边的距离随游泳时间变化的情况,请根据图象回答:
(1)甲、乙两人分别游了几个来回?
(2)甲、乙两人在整个游泳过程中,谁曾休息过?休息了几次?
(3)甲游了多长时间?游泳的速度是多少?
(4)在整个游泳过程中,甲、乙两人相遇了几次?
图19-1-16
18.2020·秦皇岛海港模拟如图19-1-21①,某容器由A,B,C三个长方体组成,其中A,B,C的底面积分别为25
cm2,10
cm2,5
cm2,C的容积是该容器容积的(容器各面的厚度忽略不计).现以速度v(单位:
cm3/s)均匀地向容器内注水,直至注满为止.图②是注水全过程中容器的水面高度h(单位:
cm)与注水时间t(单位:s)之间的函数图象.
(1)在注水过程中,注满A所用时间为________s,再注满B又用了________s;
(2)求A的高度及注水的速度v;
(3)求注满容器所需时间及容器的高度.
图19-1-21
典题讲评与答案详析
1.C 2.C
3.C [解析]
因为x≠0,所以可排除A,B.因为当x=-1时,y=-2,所以可排除D.
4.解:(1)如图.
(2)1.98(答案合理即可)
5.C
6.A [解析]
过点(2,0)作一条垂直于x轴的直线x=2,当x>2时,y的值随x值的增大而增大,说明图象在直线x=2的右侧是上升的,当x<2时,y的值随x值的增大而减小,说明图象在直线x=2的左侧是下降的.
7.(1)-4≤x≤3 (2)-2≤y≤4
(3)3 (4)1
(5)-2≤x≤1
(6)-4≤x≤-2或1≤x≤3
8.20
9.解:(1)洗衣机的进水时间是4分钟,清洗时洗衣机中的水量是40升.
(2)由图象可知,洗衣机清洗衣服所用的时间是15-4=11(分).
10.解:(1)l1描述的是小凡的运动过程.理由:
因为小凡在路边超市买了一些学习用品,需要停留一段时间,此时间段内小凡距学校的路程没有变化,所以l1描述的是小凡的运动过程.
(2)观察两函数图象,发现:小凡先出发,比小光先出发了10分钟.
(3)60-50=10(分),所以小光先到达图书馆,比小凡先到了10分钟.
(4)小凡的平均速度为5÷=10(千米/时),小光的平均速度为5÷=7.5(千米/时).
答:小凡从学校到图书馆的平均速度是10千米/时,小光从学校到图书馆的平均速度是7.5千米/时.
11.表中从上到下依次填:100 98.6 20 32
12.解:根据表格能看出当日销售单价每增加1元/件时,日销售量减少2件,
因此y=18-2(x-3)=-2x+24,即y=-2x+24.
13.解:(1)136 94
(2)当等腰直角三角形的直角边长由1
cm增加到6
cm时,阴影部分的面积由142
cm2逐渐减小到72
cm2.
(3)S=122-4××a2=-2a2+144.
14.解:(1)如图.
(2)泥茶壶中水温开始时下降幅度比塑料壶中水温下降幅度大.当两壶中水温基本稳定后,泥茶壶中的水温低于室温,而塑料壶中水温等于室温.
15.解:(1)y=5x+3
(2)当x>3时,根据题意,得y=(x-7)2+m.
把(10,11)代入,得9+m=11,解得m=2,
所以当x>3时,y与x之间的函数解析式为y=(x-7)2+2.
16.解:(1)逐渐增大 不变 逐渐减小
(2)当点P与点B重合时,S=×8×10=40(cm2).
由图象可知,当x=a时,S=24,即此时点P在边AB上,
所以S=×8×AP=24,
解得AP=6
cm,
所以a=6,此时BP=4
cm.
当x=8时,S=40,
所以8-a=2,
则b==2.
c=8+=17.
(3)y=6+2(x-6)=2x-6(6≤x≤17).
17.解:(1)甲游了3个来回,乙游了2个来回.
(2)乙曾休息过,休息了两次.
(3)甲游了180秒,游泳的速度是90×6÷180=3(米/秒).
(4)甲、乙两人相遇了5次.
18.解:(1)10 8
(2)设A的高度为a
cm,列方程组为解得
答:A的高度为4
cm,注水的速度v为10
cm3/s.
(3)18÷1-=18÷=24(s).
则10×(24-18)=5×hc,解得hc=12.
∴容器的高度为12+12=24(cm).
答:注满容器所需时间为24
s,容器的高度为24
cm.
