福建省厦门市思明区湖滨路高中2020-2021学年高二下学期期中考试数学试题 Word版含答案解析
文档属性
| 名称 | 福建省厦门市思明区湖滨路高中2020-2021学年高二下学期期中考试数学试题 Word版含答案解析 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 22:11:59 | ||
图片预览




文档简介
湖滨路高中2020---2021学年第二学期期中考
高二数学试卷
一、单选题
1.已知false为虚数单位,复数false满足false,则false的共轭复数false( )
A.false B.false C.false D.false
2.已知向量false, false, false,若false,则实数false的值为( )
A.false B.false C.false D.false
3.如图所示,已知false是平行六面体.设false, false是false上靠近点false的四等分点,若false,则false的值为( )
472440045720A.false B.false
C.false D.false
4.函数y=xlnx在(0,5)上是( )
A.单调增函数 B.在false上单调递增,在false上单调递减
C.单调减函数 D.在false上单调递减,在false上单调递增
43815005162555.已知false上可导函数false的图象如图,则不等式false的解集是(? )
A.false B.false
C.false D.false
48577507620006.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
A.false B.-false C.2 D.false
7.若false在x=1处取得极大值10,则false的值为( )
A.false或false B.false或false C.false D.false
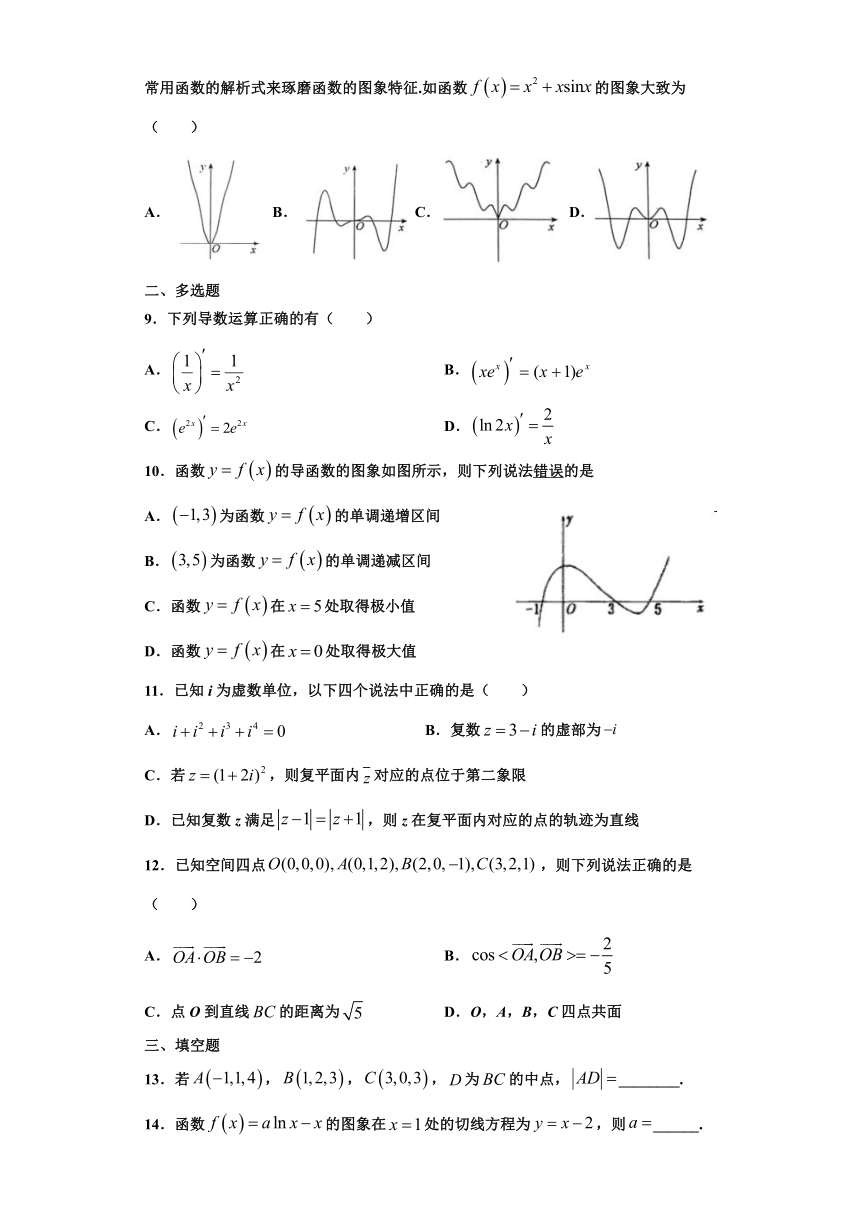
8.我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难人微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图像研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数false的图象大致为( )
A.B.C. D.
二、多选题
9.下列导数运算正确的有( )
A.false B.false
C.false D.false
10.函数false的导函数的图象如图所示,则下列说法错误的是
3238500165735A.false为函数false的单调递增区间
B.false为函数false的单调递减区间
C.函数false在false处取得极小值
D.函数false在false处取得极大值
11.已知i为虚数单位,以下四个说法中正确的是( )
A.false B.复数false的虚部为false
C.若false,则复平面内false对应的点位于第二象限
D.已知复数z满足false,则z在复平面内对应的点的轨迹为直线
12.已知空间四点false,则下列说法正确的是( )
A.false B.false
C.点O到直线false的距离为false D.O,A,B,C四点共面
三、填空题
13.若false,false,false,false为false的中点,false________.
14.函数false的图象在false处的切线方程为false,则false______.
15.定义在false上的连续函数false满足false,且false在false上的导函数false,则不等式false的解集为__________.
16.已知false在区间false上为单调递增函数,则实数false的取值范围是__________.
四、解答题
17.已知向量false与false的夹角false,且false,false.
(1)求false,false;
(2)求false与false的夹角的余弦值.
399097542291018.如图,四边形false为正方形,false平面false,点false分别为false的中点,且false,false.
(1)证明:false平面false;
(2)求二面角false的大小.
19.已知函数false在false处取得极值为false.
(1)求false、false的值;
(2)若false有极大值false,求false在false上的最大值.
20.某偏远贫困村积极响应国家“扶贫攻坚”政策,在对口帮扶单位的支持下建了一个工厂,已知每件产品的成本为false元,预计当每件产品的售价为false元false时,年销量为false万件.若每件产品的售价定为false元时,预计年利润为false万元
(1)试求每件产品的成本false的值;
(2)当每件产品的售价定为多少元时?年利润false(万元)最大,并求最大值.
339471070548521.如图1,在边长为2的菱形false中,false,false于点false,将false沿false折起到false的位置,使false,如图2.
(1)求证:false平面false;
(2)在线段false上是否存在点false,使平面false平面false?若存在,求false的值;若不存在,说明理由.
22.设函数false.
(1)当false时,求证:false;
(2)若false,使得不等式false成立,求实数a的取值范围.
高二数学试卷答案
一、单选题
1.已知false为虚数单位,复数false满足false,则false的共轭复数false
A.false B.false C.false D.false
【答案】A
【详解】
由false,得false,故选A.
2.已知向量false, false, false,若false,则实数false的值为( )
A.false B.false C.false D.false
【答案】A
3.如图所示,已知false是平行六面体.设false, false是false上靠近点false的四等分点,若false,则false的值为( )
A.false B.false
C.false D.false
【答案】A
【分析】
用空间向量运算法则,用基false表示出false即可获解.
【详解】
由题知false是false的中点,所以 false 又false是 false上靠近点 false的四等分点, 所以 false
所以 false
false
false
false
又false
所以 false
故选:A
4.函数y=xlnx在(0,5)上是( )
A.单调增函数 B.在false上单调递增,在false上单调递减
C.单调减函数 D.在false上单调递减,在false上单调递增
【答案】D
【详解】
false,由false,得极值点false当false时,false,函数是单调递减函数;当false时,false,函数是单调递增函数,即函数false 在false上单调递减,在false上单调递增,故选D.
5.已知false上可导函数false的图象如图,则不等式false的解集是(? )
A.false B.false
C.false D.false
【答案】D
【分析】
false则函数单调递增,所以从图中确定单调递增区间即可得解.
【详解】
由图可知false在false上单调递增,所以false的解集为false.
故选:D
【点睛】
本题考查导数的符号与函数单调性的关系,属于基础题.
6.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
A.false B.-false C.2 D.false
【答案】A
【分析】
如图所示,分别取false,false,false,false的中点false,false,false,false,则false,false,false,false或其补角 为异面直线false与false所成角.
【详解】
解:如图所示,
分别取false,false,false,false的中点false,false,false,false,则false,false,false,
false或其补角为异面直线false与false所成角.
设false,则false,false,
false,
false异面直线false与false所成角的余弦值为false,
故选:A.
【点睛】
平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:
①平移:平移异面直线中的一条或两条,作出异面直线所成的角;
②认定:证明作出的角就是所求异面直线所成的角;
③计算:求该角的值,常利用解三角形;
④取舍:由异面直线所成的角的取值范围是false,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.
7.若false在x=1处取得极大值10,则false的值为( )
A.false或false B.false或false C.false D.false
【答案】C
【解析】
【分析】
由于false,依题意知,false,false,于是有false,代入f(1)=10即可求得false,从而可得答案.
【详解】
∵false,∴false,
又false在x=1处取得极大值10,
∴false,false,
∴false,
∴false或false.
当false时,false,
当false<x<1时,false,当x>1时,false,
∴f(x)在x=1处取得极小值,与题意不符;
当false时,false,
当x<1时,false,当<x<3时,false,
∴f(x)在x=1处取得极大值,符合题意;则false,
故选C.
【点睛】
本题考查函数在某点取得极值的条件,求得false,利用false,f(1)=10求得false是关键,考查分析、推理与运算能力,属于中档题.
8.我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难人微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图像研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数false的图象大致为( )
A. B.
C. D.
【答案】A
【分析】
利用排除法,先判断函数的奇偶性,再判断函数的单调性即可
【详解】
由false可知,该函数为偶函数,false不对;可考虑false的情况,
false,因为false,又false
false.函数false在false上为增函数,
故选:A.
二、多选题
9.下列导数运算正确的有( )
A.false B.false
C.false D.false
【答案】BC
【分析】
根据导数的运算法则逐项运算排除可得答案.
【详解】
对于A,false,故错误;
对于B, false,故正确;
对于C, false,故正确;
对于D, false,故错误.
故选:BC.
10.函数false的导函数的图象如图所示,则下列说法错误的是
A.false为函数false的单调递增区间
B.false为函数false的单调递减区间
C.函数false在false处取得极小值
D.函数false在false处取得极大值
【答案】D
【分析】
利用导数和函数的单调性之间的关系,以及函数在某点取得极值的条件,即可求解,得到答案.
【详解】
由题意,函数false的导函数的图象可知:
当false时,false,函数false单调递减;
当false时,false,函数false单调递增;
当false时,false,函数false单调递减;
当false时,false,函数false单调递增;
所以函数false单调递减区间为false,递增区间为false,
且函数false在false和false取得极小值,在false取得极大值,
故选D.
【点睛】
本题主要考查了导函数与原函数的关系,以及函数的单调性与极值的判定,其中解答中根据导函数的图象得出原函数的单调性是解答的关键,着重考查了数形结合思想,以及推理与运算能力,属于基础题.
11.已知i为虚数单位,以下四个说法中正确的是( )
A.false
B.复数false的虚部为false
C.若false,则复平面内false对应的点位于第二象限
D.已知复数z满足false,则z在复平面内对应的点的轨迹为直线
【答案】AD
【分析】
根据复数的概念、运算对选项逐一分析,由此确定正确选项.
【详解】
A选项,false,故A选项正确.
B选项,false的虚部为false,故B选项错误.
C选项,false,对应坐标为false在第三象限,故C选项错误.
D选项,false表示false到false和false两点的距离相等,故false的轨迹是线段false的垂直平分线,故D选项正确.
故选:AD
12.已知空间四点false,则下列说法正确的是( )
A.false B.false
C.点O到直线false的距离为false D.O,A,B,C四点共面
【答案】ABC
【分析】
计算数量积判断A,求向量夹角判断B,利用向量垂直判断C,根据空间向量共面定理判断D.
【详解】
false,
false,A正确;
false,B正确;
false,false,所以false,false,所以点O到直线false的距离为false,C正确;
false,
假设若O,A,B,C四点共面,则false共面,设false,
则false,此方程组无解,所以O,A,B,C四点不共面,D错.
故选:ABC.
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.若false,false,false,false为false的中点,false________.
【答案】false
【分析】
由中点坐标公式得出false点坐标,再由空间两点距离公式得出距离
【详解】
false的坐标为false即false
falsefalse
故答案为:false
14.函数false的图象在false处的切线方程为false,则false______.
【答案】false
【分析】
利用导数和斜率的关系列方程,由此求得false的值.
【详解】
依题意false,由于函数false的图象在false处的切线方程为false,直线false的斜率为false,所以false.
故答案为:false
【点睛】
本小题主要考查根据切线方程求参数,属于基础题.
15.定义在false上的连续函数false满足false,且false在false上的导函数false,则不等式false的解集为__________.
【答案】false
【解析】
设false,则false,即false是单调递减函数,而false,所以false等价于false,即false,所以false,故不等式的解集为false,应填答案false.
点睛:本题的解答过程中,充分借助题设条件,巧妙地构造函数false,从而借助导数的求导法则及导数与函数单调性的关系,判断出该函数的单调递减函数,进而为解不等式创造出模型.解答本题的难点在于怎样观察并构造出函数,然后再用导数知识判断其单调性,进而将不等式进行等价转化.
16.已知false在区间false上为单调递增函数,则实数false的取值范围是__________.
【答案】false
【分析】
求出导函数false,由false在false上恒成立可得false的范围.
【详解】
false,由题意false在false时恒成立,
即false在false时恒成立,false,
由对勾函数性质知false在false单调递增,所以false,
所以false,即false.
故答案为:false.
【点睛】
本题考查用函数在某个区间上单调性,解题方法是把问题转化为不等式恒成立,再转化为求函数的最值.解题基础求出导函数.
四、解答题
17.已知向量false与false的夹角false,且false,false.
(1)求false,false;
(2)求false与false的夹角的余弦值.
【答案】(1)false,false;(2)false.
【分析】
(1)利用平面向量数量积的定义可计算得出false的值,利用平面向量数量积的运算性质计算得出false的值;
(2)计算出false的值,利用平面向量夹角的余弦公式可求得false与false的夹角的余弦值.
【详解】
(1)由已知,得false,
false;
(2)设false与false的夹角为false,
则false,
因此,false与false的夹角的余弦值为false.
18.如图,四边形false为正方形,false平面false,点false分别为false的中点,且false,false.
(1)证明:false平面false;
(2)求二面角false的大小.
【答案】(1)见解析(2)false.
【分析】
(1)取false的中点为false,连接false,可证四边形false为平行四边形,则false,即可得证;
(2)以false为坐标原点,false、false、false所在直线为false、false、false轴建立空间直角坐标系,利用空间向量法求出二面角的余弦值,再由特殊角的三角函数值求出角度;
【详解】
解:(1)证明:取false的中点为false,连接false
又false为false的中点,所以false,且false,
因为false,且false,
所以false,且false,
故四边形false为平行四边形,则false
又false平面false,false平面false,
所以false平面false,
(2)因为false,false,false平面false,所以false
而四边形false为正方形,所以可如图建立空间直角坐标系false
false,false,false,false
所以false,false,false
设平面false的一个法向量为false,则false
∴false,false
同理可得平面false的一个法向量为false
所以false,
由图知二面角false为钝角,则大小为false.
【点睛】
本题考查线面平行的判定,利用空间向量法求二面角,属于中档题.
19.已知函数false在false处取得极值为false.
(1)求false、false的值;
(2)若false有极大值false,求false在false上的最大值.
【答案】(1) false;(2) 最小值为false.
【解析】
试题分析:(1)false,有false,得false;(2)false在false处取得极大值false,在false处取得极小值false,最小值为false.
试题解析:
(1)因false故false由于false在点false处取得极值
故有false即false,化简得false解得false
(2).知false,false令false,得false,false
当false时,false故false在false上为增函数;
当false时,false故false在false上为减函数;
当false时,false,故false在false上为增函数.
由此可知false在false处取得极大值false.
false在false处取得极小值false
由题设条件知false得false
此时false,false,false
因此false上false的最小值为false.
20.某偏远贫困村积极响应国家“扶贫攻坚”政策,在对口帮扶单位的支持下建了一个工厂,已知每件产品的成本为false元,预计当每件产品的售价为false元false时,年销量为false万件.若每件产品的售价定为false元时,预计年利润为false万元
(1)试求每件产品的成本false的值;
(2)当每件产品的售价定为多少元时?年利润false(万元)最大,并求最大值.
【答案】(1)false;(2)每件产品的售价定为false元时,年利润false最大,最大值为false万元.
【分析】
(1)求得利润为false,代入点false可求得实数false的值;
(2)由(1)可得出false,false,利用导数求出false的最大值及其对应的false的值,即可得出结论.
【详解】
(1)由题意可知,该产品的年利润为false,false,
当false时,false,解得:false;
(2)由false,false,
得:false,
由false,得false或false(舍).
当false时,false,当false时,false.
所以当false时,false(万元)
即每件产品的售价定为false元时,年利润false最大,最大值为false万元.
【点睛】
思路点睛:解函数应用题的一般程序:
第一步:审题——弄清题意,分清条件和结论,理顺数量关系;
第二步:建模——将文字语言转化成数学语言,用数学知识建立相应的数学模型;
第三步:求模——求解数学模型,得到数学结论;
第四步:还原——将用数学方法得到的结论还原为实际问题的意义;
第五步:反思回顾——对于数学模型得到的数学结果,必须验证这个数学解对实际问题的合理性.
21.如图1,在边长为2的菱形false中,false,false于点false,将false沿false折起到false的位置,使false,如图2.
(1)求证:false平面false;
(2)在线段false上是否存在点false,使平面false平面false?若存在,求false的值;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在,且false
【分析】
(1)false,false,由线面垂直的判定定理得到false平面false,从而有false,又false,再由线面垂直的判定定理证明。
(2)假设在线段false上是否存在点false,使平面false平面false,根据(1)建立空间直角坐标系,设false,则false,所以false,若使平面false平面false,分别求得两个平面的法向量,再通过两个法向量数量积为零求解.
【详解】
(1)证明:因为false于点false,
所以false,
false,false,且false,
false平面false,
falsefalse,
false平面false.
(2)假设在线段false上是否存在点false,使平面false平面false.
根据(1)建立如图所示空间直角坐标系:
则false,false,
设false,
则false,所以false,
所以false,
设平面false一个法向量为:false,
则false,即false,
令false,所以false,
设平面false一个法向量为:false,
则false,即false,
令false,所以false,
因为平面false平面false,
所以false,即false
解得false.
所以在线段false上是否存在点false,使平面false平面false,且false.
【点睛】
本题主要考查了线面垂直的判定定理和面面垂直问题,还考查了逻辑推理,探究问题的能力,属于中档题.
22.设函数false.
(1)当false时,求证:false;
(2)若false,使得不等式false成立,求实数a的取值范围.
【答案】(1)证明见解析;(2)false.
【分析】
(1)令false,求导分析单调性求解最小值大于0即可证明;
(2)法一:令false,求导讨论分析单调性求解最小值小于或等于false即可;法二:用分析法分析每一步成立的充要条件即可求解.
【详解】
(1)证明:当false时,false,
令false,则false,
false,
false,
false函数false在false上单调递增,
false,即false.
(2)法一:令false,则false,
false,
①当false时,false恒成立,false在false上单调递增,
false,
由题意得false,解得false;
②当false时,false恒成立,false在false上单调递减,
false,
由题意得false,解得false;
③当false时,false时,false在false上单调递减;
false时,false在false上单调递增.
false,
由题意得false,即false,恒成立,
false.
综上,实数a的取值范围为false.
法二:false,使得不等式false成立
false成立
false成立,
令false,则false,
false在false上是增函数,false,
false,即实数a的取值范围为false.
【点睛】
方法点睛:已知不等式能恒成立求参数值(取值范围)问题常用的方法:
(1)函数法:讨论参数范围,借助函数单调性求解;
(2)分离参数法:先将参数分离,转化成求函数的值域或最值问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.
高二数学试卷
一、单选题
1.已知false为虚数单位,复数false满足false,则false的共轭复数false( )
A.false B.false C.false D.false
2.已知向量false, false, false,若false,则实数false的值为( )
A.false B.false C.false D.false
3.如图所示,已知false是平行六面体.设false, false是false上靠近点false的四等分点,若false,则false的值为( )
472440045720A.false B.false
C.false D.false
4.函数y=xlnx在(0,5)上是( )
A.单调增函数 B.在false上单调递增,在false上单调递减
C.单调减函数 D.在false上单调递减,在false上单调递增
43815005162555.已知false上可导函数false的图象如图,则不等式false的解集是(? )
A.false B.false
C.false D.false
48577507620006.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
A.false B.-false C.2 D.false
7.若false在x=1处取得极大值10,则false的值为( )
A.false或false B.false或false C.false D.false
8.我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难人微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图像研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数false的图象大致为( )
A.B.C. D.
二、多选题
9.下列导数运算正确的有( )
A.false B.false
C.false D.false
10.函数false的导函数的图象如图所示,则下列说法错误的是
3238500165735A.false为函数false的单调递增区间
B.false为函数false的单调递减区间
C.函数false在false处取得极小值
D.函数false在false处取得极大值
11.已知i为虚数单位,以下四个说法中正确的是( )
A.false B.复数false的虚部为false
C.若false,则复平面内false对应的点位于第二象限
D.已知复数z满足false,则z在复平面内对应的点的轨迹为直线
12.已知空间四点false,则下列说法正确的是( )
A.false B.false
C.点O到直线false的距离为false D.O,A,B,C四点共面
三、填空题
13.若false,false,false,false为false的中点,false________.
14.函数false的图象在false处的切线方程为false,则false______.
15.定义在false上的连续函数false满足false,且false在false上的导函数false,则不等式false的解集为__________.
16.已知false在区间false上为单调递增函数,则实数false的取值范围是__________.
四、解答题
17.已知向量false与false的夹角false,且false,false.
(1)求false,false;
(2)求false与false的夹角的余弦值.
399097542291018.如图,四边形false为正方形,false平面false,点false分别为false的中点,且false,false.
(1)证明:false平面false;
(2)求二面角false的大小.
19.已知函数false在false处取得极值为false.
(1)求false、false的值;
(2)若false有极大值false,求false在false上的最大值.
20.某偏远贫困村积极响应国家“扶贫攻坚”政策,在对口帮扶单位的支持下建了一个工厂,已知每件产品的成本为false元,预计当每件产品的售价为false元false时,年销量为false万件.若每件产品的售价定为false元时,预计年利润为false万元
(1)试求每件产品的成本false的值;
(2)当每件产品的售价定为多少元时?年利润false(万元)最大,并求最大值.
339471070548521.如图1,在边长为2的菱形false中,false,false于点false,将false沿false折起到false的位置,使false,如图2.
(1)求证:false平面false;
(2)在线段false上是否存在点false,使平面false平面false?若存在,求false的值;若不存在,说明理由.
22.设函数false.
(1)当false时,求证:false;
(2)若false,使得不等式false成立,求实数a的取值范围.
高二数学试卷答案
一、单选题
1.已知false为虚数单位,复数false满足false,则false的共轭复数false
A.false B.false C.false D.false
【答案】A
【详解】
由false,得false,故选A.
2.已知向量false, false, false,若false,则实数false的值为( )
A.false B.false C.false D.false
【答案】A
3.如图所示,已知false是平行六面体.设false, false是false上靠近点false的四等分点,若false,则false的值为( )
A.false B.false
C.false D.false
【答案】A
【分析】
用空间向量运算法则,用基false表示出false即可获解.
【详解】
由题知false是false的中点,所以 false 又false是 false上靠近点 false的四等分点, 所以 false
所以 false
false
false
false
又false
所以 false
故选:A
4.函数y=xlnx在(0,5)上是( )
A.单调增函数 B.在false上单调递增,在false上单调递减
C.单调减函数 D.在false上单调递减,在false上单调递增
【答案】D
【详解】
false,由false,得极值点false当false时,false,函数是单调递减函数;当false时,false,函数是单调递增函数,即函数false 在false上单调递减,在false上单调递增,故选D.
5.已知false上可导函数false的图象如图,则不等式false的解集是(? )
A.false B.false
C.false D.false
【答案】D
【分析】
false则函数单调递增,所以从图中确定单调递增区间即可得解.
【详解】
由图可知false在false上单调递增,所以false的解集为false.
故选:D
【点睛】
本题考查导数的符号与函数单调性的关系,属于基础题.
6.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC与BD所成角的余弦值为( )
A.false B.-false C.2 D.false
【答案】A
【分析】
如图所示,分别取false,false,false,false的中点false,false,false,false,则false,false,false,false或其补角 为异面直线false与false所成角.
【详解】
解:如图所示,
分别取false,false,false,false的中点false,false,false,false,则false,false,false,
false或其补角为异面直线false与false所成角.
设false,则false,false,
false,
false异面直线false与false所成角的余弦值为false,
故选:A.
【点睛】
平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:
①平移:平移异面直线中的一条或两条,作出异面直线所成的角;
②认定:证明作出的角就是所求异面直线所成的角;
③计算:求该角的值,常利用解三角形;
④取舍:由异面直线所成的角的取值范围是false,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.
7.若false在x=1处取得极大值10,则false的值为( )
A.false或false B.false或false C.false D.false
【答案】C
【解析】
【分析】
由于false,依题意知,false,false,于是有false,代入f(1)=10即可求得false,从而可得答案.
【详解】
∵false,∴false,
又false在x=1处取得极大值10,
∴false,false,
∴false,
∴false或false.
当false时,false,
当false<x<1时,false,当x>1时,false,
∴f(x)在x=1处取得极小值,与题意不符;
当false时,false,
当x<1时,false,当<x<3时,false,
∴f(x)在x=1处取得极大值,符合题意;则false,
故选C.
【点睛】
本题考查函数在某点取得极值的条件,求得false,利用false,f(1)=10求得false是关键,考查分析、推理与运算能力,属于中档题.
8.我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难人微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图像研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数false的图象大致为( )
A. B.
C. D.
【答案】A
【分析】
利用排除法,先判断函数的奇偶性,再判断函数的单调性即可
【详解】
由false可知,该函数为偶函数,false不对;可考虑false的情况,
false,因为false,又false
false.函数false在false上为增函数,
故选:A.
二、多选题
9.下列导数运算正确的有( )
A.false B.false
C.false D.false
【答案】BC
【分析】
根据导数的运算法则逐项运算排除可得答案.
【详解】
对于A,false,故错误;
对于B, false,故正确;
对于C, false,故正确;
对于D, false,故错误.
故选:BC.
10.函数false的导函数的图象如图所示,则下列说法错误的是
A.false为函数false的单调递增区间
B.false为函数false的单调递减区间
C.函数false在false处取得极小值
D.函数false在false处取得极大值
【答案】D
【分析】
利用导数和函数的单调性之间的关系,以及函数在某点取得极值的条件,即可求解,得到答案.
【详解】
由题意,函数false的导函数的图象可知:
当false时,false,函数false单调递减;
当false时,false,函数false单调递增;
当false时,false,函数false单调递减;
当false时,false,函数false单调递增;
所以函数false单调递减区间为false,递增区间为false,
且函数false在false和false取得极小值,在false取得极大值,
故选D.
【点睛】
本题主要考查了导函数与原函数的关系,以及函数的单调性与极值的判定,其中解答中根据导函数的图象得出原函数的单调性是解答的关键,着重考查了数形结合思想,以及推理与运算能力,属于基础题.
11.已知i为虚数单位,以下四个说法中正确的是( )
A.false
B.复数false的虚部为false
C.若false,则复平面内false对应的点位于第二象限
D.已知复数z满足false,则z在复平面内对应的点的轨迹为直线
【答案】AD
【分析】
根据复数的概念、运算对选项逐一分析,由此确定正确选项.
【详解】
A选项,false,故A选项正确.
B选项,false的虚部为false,故B选项错误.
C选项,false,对应坐标为false在第三象限,故C选项错误.
D选项,false表示false到false和false两点的距离相等,故false的轨迹是线段false的垂直平分线,故D选项正确.
故选:AD
12.已知空间四点false,则下列说法正确的是( )
A.false B.false
C.点O到直线false的距离为false D.O,A,B,C四点共面
【答案】ABC
【分析】
计算数量积判断A,求向量夹角判断B,利用向量垂直判断C,根据空间向量共面定理判断D.
【详解】
false,
false,A正确;
false,B正确;
false,false,所以false,false,所以点O到直线false的距离为false,C正确;
false,
假设若O,A,B,C四点共面,则false共面,设false,
则false,此方程组无解,所以O,A,B,C四点不共面,D错.
故选:ABC.
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
13.若false,false,false,false为false的中点,false________.
【答案】false
【分析】
由中点坐标公式得出false点坐标,再由空间两点距离公式得出距离
【详解】
false的坐标为false即false
falsefalse
故答案为:false
14.函数false的图象在false处的切线方程为false,则false______.
【答案】false
【分析】
利用导数和斜率的关系列方程,由此求得false的值.
【详解】
依题意false,由于函数false的图象在false处的切线方程为false,直线false的斜率为false,所以false.
故答案为:false
【点睛】
本小题主要考查根据切线方程求参数,属于基础题.
15.定义在false上的连续函数false满足false,且false在false上的导函数false,则不等式false的解集为__________.
【答案】false
【解析】
设false,则false,即false是单调递减函数,而false,所以false等价于false,即false,所以false,故不等式的解集为false,应填答案false.
点睛:本题的解答过程中,充分借助题设条件,巧妙地构造函数false,从而借助导数的求导法则及导数与函数单调性的关系,判断出该函数的单调递减函数,进而为解不等式创造出模型.解答本题的难点在于怎样观察并构造出函数,然后再用导数知识判断其单调性,进而将不等式进行等价转化.
16.已知false在区间false上为单调递增函数,则实数false的取值范围是__________.
【答案】false
【分析】
求出导函数false,由false在false上恒成立可得false的范围.
【详解】
false,由题意false在false时恒成立,
即false在false时恒成立,false,
由对勾函数性质知false在false单调递增,所以false,
所以false,即false.
故答案为:false.
【点睛】
本题考查用函数在某个区间上单调性,解题方法是把问题转化为不等式恒成立,再转化为求函数的最值.解题基础求出导函数.
四、解答题
17.已知向量false与false的夹角false,且false,false.
(1)求false,false;
(2)求false与false的夹角的余弦值.
【答案】(1)false,false;(2)false.
【分析】
(1)利用平面向量数量积的定义可计算得出false的值,利用平面向量数量积的运算性质计算得出false的值;
(2)计算出false的值,利用平面向量夹角的余弦公式可求得false与false的夹角的余弦值.
【详解】
(1)由已知,得false,
false;
(2)设false与false的夹角为false,
则false,
因此,false与false的夹角的余弦值为false.
18.如图,四边形false为正方形,false平面false,点false分别为false的中点,且false,false.
(1)证明:false平面false;
(2)求二面角false的大小.
【答案】(1)见解析(2)false.
【分析】
(1)取false的中点为false,连接false,可证四边形false为平行四边形,则false,即可得证;
(2)以false为坐标原点,false、false、false所在直线为false、false、false轴建立空间直角坐标系,利用空间向量法求出二面角的余弦值,再由特殊角的三角函数值求出角度;
【详解】
解:(1)证明:取false的中点为false,连接false
又false为false的中点,所以false,且false,
因为false,且false,
所以false,且false,
故四边形false为平行四边形,则false
又false平面false,false平面false,
所以false平面false,
(2)因为false,false,false平面false,所以false
而四边形false为正方形,所以可如图建立空间直角坐标系false
false,false,false,false
所以false,false,false
设平面false的一个法向量为false,则false
∴false,false
同理可得平面false的一个法向量为false
所以false,
由图知二面角false为钝角,则大小为false.
【点睛】
本题考查线面平行的判定,利用空间向量法求二面角,属于中档题.
19.已知函数false在false处取得极值为false.
(1)求false、false的值;
(2)若false有极大值false,求false在false上的最大值.
【答案】(1) false;(2) 最小值为false.
【解析】
试题分析:(1)false,有false,得false;(2)false在false处取得极大值false,在false处取得极小值false,最小值为false.
试题解析:
(1)因false故false由于false在点false处取得极值
故有false即false,化简得false解得false
(2).知false,false令false,得false,false
当false时,false故false在false上为增函数;
当false时,false故false在false上为减函数;
当false时,false,故false在false上为增函数.
由此可知false在false处取得极大值false.
false在false处取得极小值false
由题设条件知false得false
此时false,false,false
因此false上false的最小值为false.
20.某偏远贫困村积极响应国家“扶贫攻坚”政策,在对口帮扶单位的支持下建了一个工厂,已知每件产品的成本为false元,预计当每件产品的售价为false元false时,年销量为false万件.若每件产品的售价定为false元时,预计年利润为false万元
(1)试求每件产品的成本false的值;
(2)当每件产品的售价定为多少元时?年利润false(万元)最大,并求最大值.
【答案】(1)false;(2)每件产品的售价定为false元时,年利润false最大,最大值为false万元.
【分析】
(1)求得利润为false,代入点false可求得实数false的值;
(2)由(1)可得出false,false,利用导数求出false的最大值及其对应的false的值,即可得出结论.
【详解】
(1)由题意可知,该产品的年利润为false,false,
当false时,false,解得:false;
(2)由false,false,
得:false,
由false,得false或false(舍).
当false时,false,当false时,false.
所以当false时,false(万元)
即每件产品的售价定为false元时,年利润false最大,最大值为false万元.
【点睛】
思路点睛:解函数应用题的一般程序:
第一步:审题——弄清题意,分清条件和结论,理顺数量关系;
第二步:建模——将文字语言转化成数学语言,用数学知识建立相应的数学模型;
第三步:求模——求解数学模型,得到数学结论;
第四步:还原——将用数学方法得到的结论还原为实际问题的意义;
第五步:反思回顾——对于数学模型得到的数学结果,必须验证这个数学解对实际问题的合理性.
21.如图1,在边长为2的菱形false中,false,false于点false,将false沿false折起到false的位置,使false,如图2.
(1)求证:false平面false;
(2)在线段false上是否存在点false,使平面false平面false?若存在,求false的值;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在,且false
【分析】
(1)false,false,由线面垂直的判定定理得到false平面false,从而有false,又false,再由线面垂直的判定定理证明。
(2)假设在线段false上是否存在点false,使平面false平面false,根据(1)建立空间直角坐标系,设false,则false,所以false,若使平面false平面false,分别求得两个平面的法向量,再通过两个法向量数量积为零求解.
【详解】
(1)证明:因为false于点false,
所以false,
false,false,且false,
false平面false,
falsefalse,
false平面false.
(2)假设在线段false上是否存在点false,使平面false平面false.
根据(1)建立如图所示空间直角坐标系:
则false,false,
设false,
则false,所以false,
所以false,
设平面false一个法向量为:false,
则false,即false,
令false,所以false,
设平面false一个法向量为:false,
则false,即false,
令false,所以false,
因为平面false平面false,
所以false,即false
解得false.
所以在线段false上是否存在点false,使平面false平面false,且false.
【点睛】
本题主要考查了线面垂直的判定定理和面面垂直问题,还考查了逻辑推理,探究问题的能力,属于中档题.
22.设函数false.
(1)当false时,求证:false;
(2)若false,使得不等式false成立,求实数a的取值范围.
【答案】(1)证明见解析;(2)false.
【分析】
(1)令false,求导分析单调性求解最小值大于0即可证明;
(2)法一:令false,求导讨论分析单调性求解最小值小于或等于false即可;法二:用分析法分析每一步成立的充要条件即可求解.
【详解】
(1)证明:当false时,false,
令false,则false,
false,
false,
false函数false在false上单调递增,
false,即false.
(2)法一:令false,则false,
false,
①当false时,false恒成立,false在false上单调递增,
false,
由题意得false,解得false;
②当false时,false恒成立,false在false上单调递减,
false,
由题意得false,解得false;
③当false时,false时,false在false上单调递减;
false时,false在false上单调递增.
false,
由题意得false,即false,恒成立,
false.
综上,实数a的取值范围为false.
法二:false,使得不等式false成立
false成立
false成立,
令false,则false,
false在false上是增函数,false,
false,即实数a的取值范围为false.
【点睛】
方法点睛:已知不等式能恒成立求参数值(取值范围)问题常用的方法:
(1)函数法:讨论参数范围,借助函数单调性求解;
(2)分离参数法:先将参数分离,转化成求函数的值域或最值问题加以解决;
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.
同课章节目录
