湘教版2020--2021学年度八年级下期末数学模拟试卷2(含解析)
文档属性
| 名称 | 湘教版2020--2021学年度八年级下期末数学模拟试卷2(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 06:22:21 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
湘教教版八年级下期末模拟试卷2
姓名:__________班级:__________考号:__________总分__________
、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
在平面直角坐标系中,点P在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
在学习《图形变化的简单应用》这一节时,老师要求同学们利用图形变化设计图案.下列设计的图案中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方B点共四圈,已知易拉罐底面周长是12cm,高是20cm,那么所需彩带最短的是( )
A.13cm B.4cm C.4cm D.52cm
菱形,矩形,正方形都具有的性质是( )
A.对角线相等且互相平分 B.对角线相等且互相垂直平分
C.对角线互相平分 D.四条边相等,四个角相等
某地区用电量与应缴电费之间的关系如表:
用电量(千瓦·时) 1 2 3 4 …
应缴电费(元) 0.55 1.10 1.65 2.20 …
则下列叙述错误的是( )
A.若所缴电费为2.75元,则用电量为6千瓦·时
B.若用电量为8千瓦·时,则应缴电费4.4元
C.用电量每增加1千瓦·时,电费增加0.55元
D.所缴电费随用电量的增加而增加
正比例函数y=﹣3x的大致图象是( )
为了描述我国近年来GDP(国内生产总值)的变化趋势,选用的统计图最好是( )
A.条形统计图 B.折线统计图 C.扇形统计图 D.直方图
如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得 AM的长为1.2km,则M,C两点间的距离为(?? )
A.0.5 km????B.0.6 km????C.0.9 km?????D.1.2 km
平面直角坐标系中,点A(-3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的长度最小时点C的坐标为( )
A. B. C. D.
在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
A.∠ADE=20° B.∠ADE=30° C.∠ADE=∠ADC D.∠ADE=∠ADC
如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A. B. C. D.
x为任意实数,令F(x)表示{2x+1,x+2,﹣x+6}中的最小值,则F(x)的最大值是( )
A.0 B.2 C.4 D.6
、填空题(本大题共6小题,每小题3分,共18分)
八边形的内角和为 .
如图,△ABC中,∠A=∠ABC,AC=6,BD⊥AC于点D,E为BC的中点,连接DE.则DE=____________.
气象局要统计一昼夜气温变化情况,应选用___统计图.
函数中,自变量的取值范围是_____.
在平面直角坐标系中,点A是y轴上一点,若它的坐标为(a﹣1,a+1),另一点B的坐标为(a+3,a﹣5),则点B的坐标是 .
如图,边长为2a的正方形EFGH在边长为6a的正方形ABCD所在平面上移动,始终保持EF∥AB,线段CF的中点为M,DH的中点为N,则线段MN的长为 .
、解答题(本大题共8小题,共66分)
正方形的边长为2,建立适当的直角坐标系,使它的一个顶点的坐标为(,0),并写出另外三个顶点的坐标.
如图,在中,,点在上,若,平分.
(1)求的长;
(2)若是中点,求线段的长.
已知:如图,正比例函数y=kx的图象经过点A,
(1)请你求出该正比例函数的解析式;
(2)若这个函数的图象还经过点B(m,m+3),请你求出m的值;
(3)请你判断点P(﹣,1)是否在这个函数的图象上,为什么?
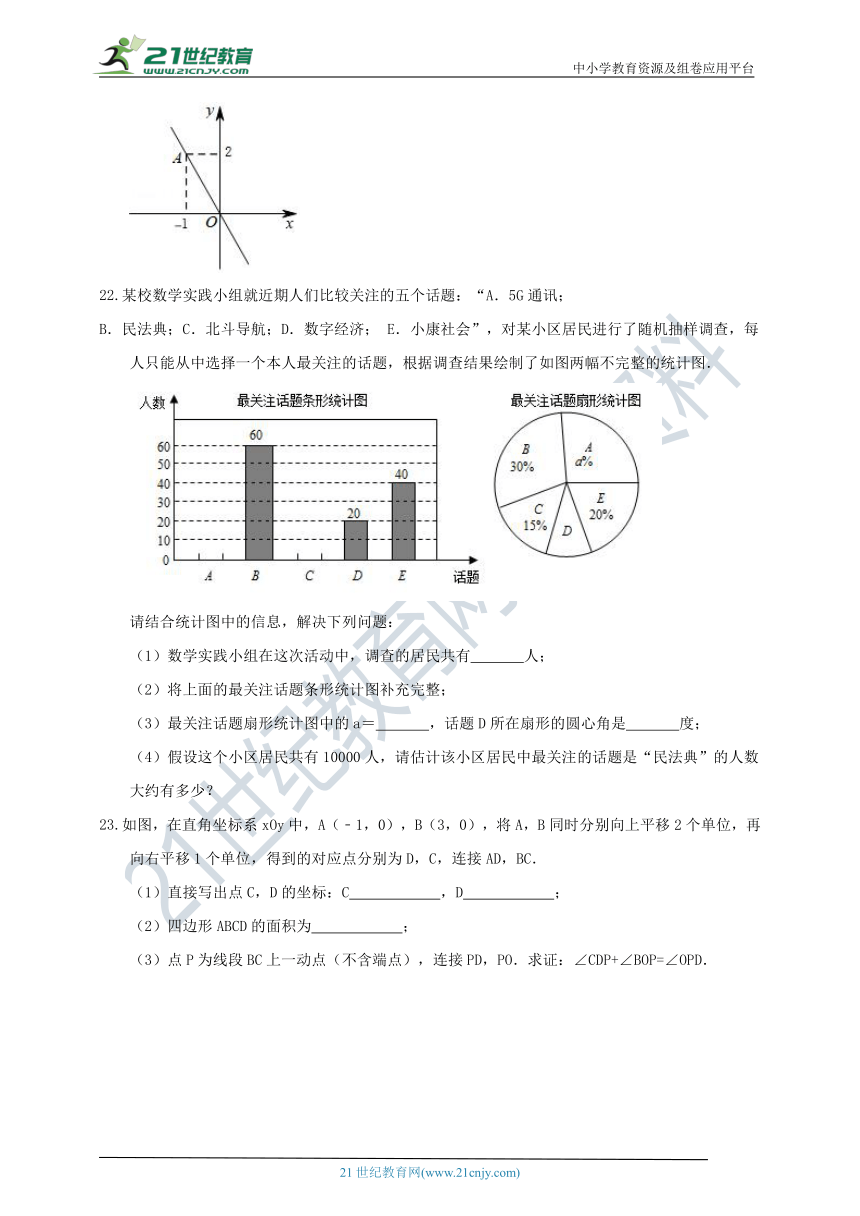
某校数学实践小组就近期人们比较关注的五个话题:“A.5G通讯;
B.民法典;C.北斗导航;D.数字经济; E.小康社会”,对某小区居民进行了随机抽样调查,每人只能从中选择一个本人最关注的话题,根据调查结果绘制了如图两幅不完整的统计图.
请结合统计图中的信息,解决下列问题:
(1)数学实践小组在这次活动中,调查的居民共有 人;
(2)将上面的最关注话题条形统计图补充完整;
(3)最关注话题扇形统计图中的a= ,话题D所在扇形的圆心角是 度;
(4)假设这个小区居民共有10000人,请估计该小区居民中最关注的话题是“民法典”的人数大约有多少?
如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.
(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
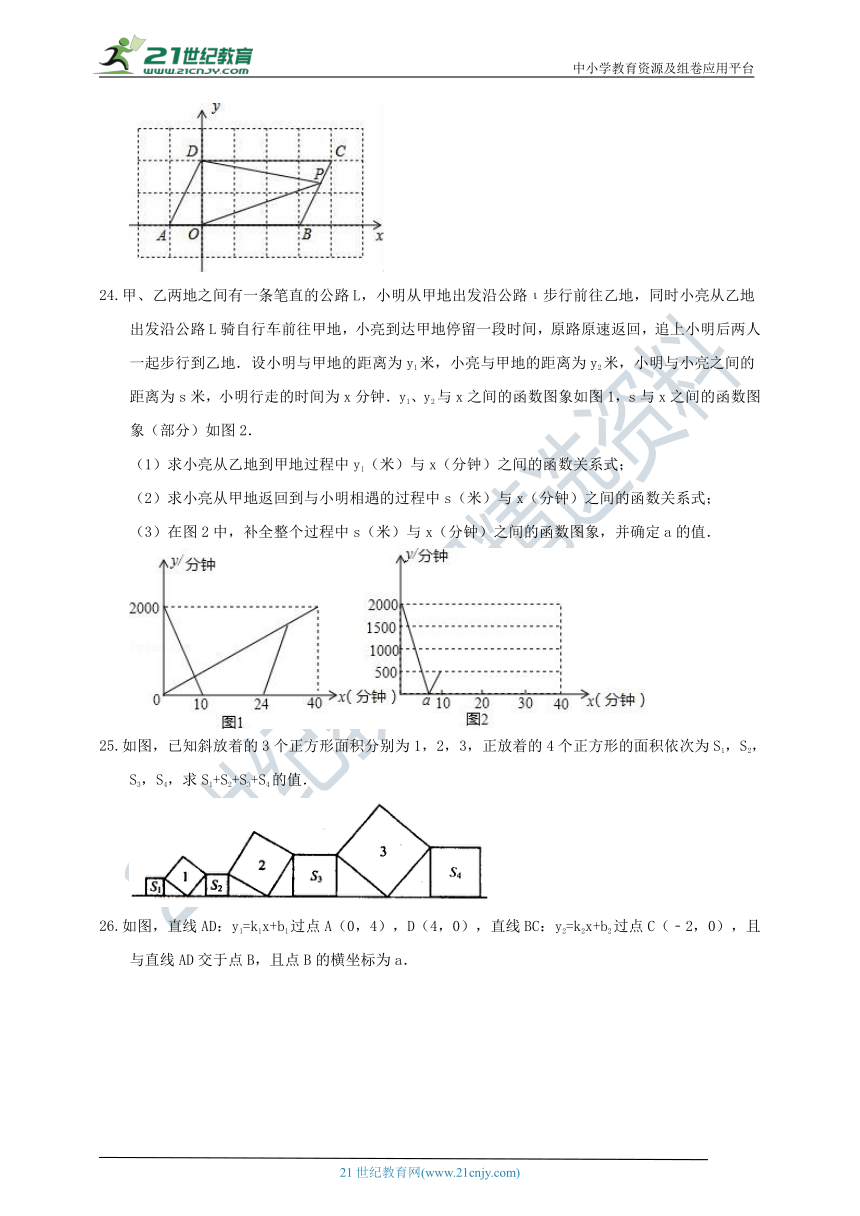
甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路ι步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.
(1)求小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式;
(2)求小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
(3)在图2中,补全整个过程中s(米)与x(分钟)之间的函数图象,并确定a的值.
如图,已知斜放着的3个正方形面积分别为1,2,3,正放着的4个正方形的面积依次为S1,S2,S3,S4,求S1+S2+S3+S4的值.
如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(﹣2,0),且与直线AD交于点B,且点B的横坐标为a.
(1)当a=1时,求直线BC的解析式;
(2)在(1)的条件下,请直接写出k1x+b1>k2x+b2时,对应的x的取值范围;
(3)设的面积为S,用含a的代数式表示S,并求出当直线CB把的面积分为1:2的两部分时,对应a的值.
答案解析
、选择题
【考点】点的坐标.
【分析】点P的横、纵坐标均为正,可确定在第一象限.
解:点P的横、纵坐标均为正,所以点P在第一象限,故选A.
【点评】本题主要考查了平面直角坐标系中第二象限的点的坐标的符号特点.四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
【考点】中心对称图形,轴对称图形
【分析】根据轴对称图形与中心对称图形的概念求解.
解:A.是轴对称图形,不是中心对称图形,故此选项错误;
B、是轴对称图形,也是中心对称图形,故此选项错误;
C、不是轴对称图形,是中心对称图形,故此选项正确;
D、是轴对称图形,也是中心对称图形,故此选项错误.
故选:C.
【点评】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
【考点】平面展开﹣最短路径问题.
【分析】要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理.
解:由图可知,彩带从易拉罐底端的A处绕易拉罐4圈后到达顶端的B处,将易拉罐表面切开展开呈长方形,则螺旋线长为四个长方形并排后的长方形的对角线长,
∵易拉罐底面周长是12cm,高是20cm,
∴x2=(12×4)2+202,
所以彩带最短是52cm.
故选D
【点评】本题考查了平面展开-最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.
【考点】正方形的性质;菱形的性质;矩形的性质.
【分析】对菱形对角线相互垂直平分,矩形对角线平分相等,正方形对角线相互垂直平分相等的性质进行分析从而得到其共有的性质.
解:A.不正确,菱形的对角线不相等;
B、不正确,菱形的对角线不相等,矩形的对角线不垂直;
C、正确,三者均具有此性质;
D、不正确,矩形的四边不相等,菱形的四个角不相等;
故选C.
【点评】熟练掌握菱形,矩形,正方形都具有的性质是解决本题的关键.
【考点】用表格表示变量之间的关系
【分析】电量从1千瓦·时到2千瓦·时,电费增加了1.1-0.55=0.55元,从2千瓦·时到3千瓦·时,电费增加了1.65-1.1=0.55元,从3千瓦·时到4千瓦·时,电费增加了2.20-1.65=0.55元,故用电量每增加1千瓦·时,电费增加0.55元,据此可回答问题.
解:A. 若所缴电费为2.75元时,电费为2.75÷0.55=5千瓦·时,故本选项错误;
B. 若用电量为8千瓦·时,电费为8×0.55=4.4元,故本选项正确;
C. 用电量每增加1千瓦·时,电费增加0.55元,故本选项正确;
D. 随着用电量增加,电费在逐渐增长,故本选项正确.
所以选A.
【点评】本题考查用表格表示变量之间的关系,解决本类题的关键是要观察表格,因变量是如何随着自变量改变的.
【考点】正比例函数的图象
【分析】正比例函数图象是经过原点的一条直线,根据y=kx中k的符号确定其所经过的象限.
解:正比例函数y=﹣3x的图象是经过原点的一条直线.
∵﹣3<0,
∴该直线经过第二、四象限.
观察选项,只有C选项符合条件.
故选:C.
【点评】考查了正比例函数的图象,正比例函数y=kx的图象是直线,当k>0时,直线经过第一、三象限;当k<0时,直线经过第二、四象限.
【考点】统计图的选择
【分析】根据统计图的特点进行选择:扇形统计图表示的是部分在总体中所占的百分比;折线统计图表示的是事物的变化情况;而条形统计图和直方图能清楚地表示出每个项目的具体数目;直方图能够清楚地表示出每组的具体数目,分组的时候,数据是连续的.
解:为了描述我国近年来GDP(国内生产总值)的变化趋势,选用的统计图最好是折线统计图.
所以B选项是正确的.
【点睛】本题考查了统计图的选择,属于简单题,熟悉统计图的特点是解题关键.
【考点】直角三角形斜边上的中线
【分析】根据直角三角形斜边的中线等于斜边的一半即可解决问题.
解:在Rt△ACB中, ∵∠ACB=90°,AM=BM,
∴CM= AB=AM,
∵AM=1.2km,
∴CM=1.2km,
故选D.
【点评】本题考查直角三角形的性质,解题的关键是掌握直角三角形斜边的中线等于斜边的一半的应用,属于中考常考题型.
【考点】坐标与图形的性质,垂线段的性质
【分析】由AC∥x轴,可得点C与点A的纵坐标相同,再根据垂线段最短可知BC⊥AC时,BC有最小值,从而可确定点C的坐标.
解:如图所示:
由垂线段最短可知:当BC⊥AC时,BC有最小值.
所以点C的坐标为(3,2),线段的最小值为2.
故选B.
【点睛】本题主要考查的是两点间的距离公式、垂线段的性质、点的坐标的定义,掌握垂线段的性质是解题的关键.
【考点】多边形内角与外角;三角形内角和定理.
【分析】利用三角形的内角和为180°,四边形的内角和为360°,分别表示出∠A,∠B,∠C,根据∠A=∠B=∠C,得到∠ADE=∠EDC,因为∠ADC=∠ADE+∠EDC=∠EDC+∠EDC=∠EDC,所以∠ADE=∠ADC,即可解答.
解:如图,
在△AED中,∠AED=60°,
∴∠A=180°﹣∠AED﹣∠ADE=120°﹣∠ADE,
在四边形DEBC中,∠DEB=180°﹣∠AED=180°﹣60°=120°,
∴∠B=∠C=(360°﹣∠DEB﹣∠EDC)÷2=120°﹣∠EDC,
∵∠A=∠B=∠C,
∴120°﹣∠ADE=120°﹣∠EDC,
∴∠ADE=∠EDC,
∵∠ADC=∠ADE+∠EDC=∠EDC+∠EDC=∠EDC,
∴∠ADE=∠ADC,
故选:D.
【点评】本题考查了多边形的内角和,解决本题的关键是熟记四边形的内角和为360°.
【考点】菱形的性质,轴对称-最短路线问题
【分析】作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP=NQ最小,NQ为所求,当NQ⊥AB时,NQ最小,继而利用面积法求出NQ长即可得答案.
解:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP=NQ最小,NQ为所求,当NQ⊥AB时,NQ最小,
∵四边形ABCD是菱形,AC=6,DB=8,
∴OA=3,OB=4,AC⊥BD,
在Rt△AOB中,AB==5,
∵S菱形ABCD=,
∴,
∴NQ=,
∴PM+PN的最小值为,
故选D.
【点睛】本题考查了菱形的性质,轴对称确定最短路线问题,熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键.
【考点】一次函数综合应用以及一次函数增减
【分析】根据已知设y1=2x+1,y2=x+2,y3=﹣x+6,进而求出图象交点坐标,进而得出此时的最值,最后比较得出答案.
解:设y1=2x+1,y2=x+2,y3=﹣x+6,
∵2x+1=x+2,
解得:x=1,则y=3,
∴y1,y2,交于(1,3),
∵x+2=﹣x+6,
解得:x=2,则y=4,
∴y2,y3交于(2,4),
∵2x+1=﹣x+6,
解得:x=,则y=,
∴y1,y3交于(,),
根据图象当x<1,F(x)=y1,此时函数的最值小于3,
当1≤x<,F(x)=y2,此时函数的最值小于,
当x≥2,F(x)=y3,此时函数的最值小于等于4,
故F(x)的最大值是4.
故选;C.
【点评】此题主要考查了一次函数综合应用以及一次函数增减性,利用数形结合得出是解题关键.
、填空题
【考点】多边形内角与外角.
【分析】根据多边形的内角和公式(n﹣2)?180°进行计算即可得解.
解:(8﹣2)?180°=6×180°=1080°.
故答案为:1080°.
【点评】本题考查了多边形的内角和,熟记内角和公式是解题的关键.
【考点】直角三角形斜边上的中线,等腰三角形的判定与性质
【分析】利用等腰三角形的判定与性质求出CA=CB=6,再利用直角三角形斜边上的中线求出BC=2DE,得出DE
解:∵∠A=∠ABC,
∴CA=CB,
∵BD⊥AC,
∴∠BDC=90°.
∵E为CB的中点,
∴BC=2DE,
∴6=2DE,
则DE=3.
故本题应填3.
【点评】直角三角形斜边上的中线,等腰三角形的判定与性质,熟练掌握各性质定理是解题的关键
【考点】统计图的选择
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.
解:因为折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况,
所以要统计一昼夜气温变化情况,应选用折线统计图;
故答案为:折线.
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.
【考点】函数自变量的取值范围
【分析】根据被开方式是非负数列式求解即可.
解:依题意,得,
解得:,
故答案为.
【点睛】本题考查了函数自变量的取值范围,函数有意义时字母的取值范围一般从几个方面考虑:①当函数解析式是整式时,字母可取全体实数;②当函数解析式是分式时,考虑分式的分母不能为0;③当函数解析式是二次根式时,被开方数为非负数.④对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.
【考点】点的坐标.
【分析】点在y轴上,则其横坐标是0.
解:∵点A(a﹣1,a+1)是y轴上一点,
∴a﹣1=0,
解得a=1,
∴a+3=1+3=4,a﹣5=1﹣5=﹣4,
∴点B的坐标是(4,﹣4).故答案填:(4,﹣4).
【点评】本题考查了坐标轴上的点的坐标的特征:点在y轴上时,其横坐标是0.
【考点】三角形中位线定理;全等三角形的判定与性质;勾股定理;正方形的性质.
【分析】因为题目没有确定正方形EFGH的位置,所以我们可以将正方形EFGH的位置特殊化,使点H与点A重合,重新作出图形,这样有利于我们解题,过点M作MO⊥ED与O,则可得出OM是梯形FEDC的中位线,从而可求出ON、OM,然后在RT△MON中利用勾股定理可求出MN.
解:如图,将正方形EFGH的位置特殊化,使点H与点A重合,过点M作MO⊥ED与O,则MO是梯形FEDC的中位线,
∴EO=OD=4a,MO=(EF+CD)=4a.
∵点N、M分别是AD、FC的中点,
∴AN=ND=3a,
∴ON=OD﹣ND=4a﹣3a=a.
在Rt△MON中,MN2=MO2+ON2,即MN===a.
故答案是: a.
【点评】本题考查了梯形的中位线定理、正方形的性质及勾股定理的知识,属于综合性题目,对待这样既有动态因素又不确定位置的题目,一定要将位置特殊化,这样不影响结果且解题过程简单,同学们要学会在以后的解题中利用这种思想.
、解答题
【考点】正方形的性质;坐标与图形性质.
【分析】先找到A(,0),根据正方形的对称性,可知A点的对称点C的坐标,同样可得出B和D的坐标.
解:建立坐标轴,使正方形的对称中心为原点,
则A(,0),C(﹣,0),
那么B的坐标是(0,),
其对称点D的坐标是(0,﹣).
【点评】本题利用了正方形既是轴对称图形又是中心对称图形的性质.
【考点】三角形中位线定理,等边三角形的性质
【分析】(1)先证明△ABD是等腰三角形,再根据三线合一得到,利用勾股定理求得AE的长;
(2)利用三角线的中位线定理可得:,再进行求解.
解:(1)
∴
∵平分,
∴
根据勾股定理,得
(2)由(1),知,
又∵,
∴.
【点睛】考查了三角形中位线定理,解题关键是利用三线合一和三角形的中位线.
【考点】一次函数图象上点的坐标特征;待定系数法求正比例函数解析式
【分析】(1)将点A(﹣1,2)代入y=kx求得k的值即可得;
(2)将点B坐标代入函数解析式可得m的方程,解之即可得;
(3)在所求函数解析式中求出x=﹣时y的值,看是否等于1即可得出结论.
解:(1)由图可知点A(﹣1,2),代入y=kx得:
﹣k=2,k=﹣2,
则正比例函数解析式为y=﹣2x;
(2)将点B(m,m+3)代入y=﹣2x,得:﹣2m=m+3,
解得:m=﹣1;
(3)当x=﹣时,y=﹣2×(﹣)=3≠1,
所以点P不在这个函数图象上.
【点评】本题主要考查待定系数法求出一次函数解析式,解题的关键是熟练掌握待定系数法求函数解析式及一次函数图象上点的坐标特征.
【考点】条形统计图,扇形统计图,用样本估计总体
【分析】(1)根据选择B的人数和所占的百分比,可以求得本次调查的居民人数;(2)根据(1)中的结果和统计图中的数据,可以计算出选择A和C的人数,从而可以将条形统计图补充完整;(3)根据统计图中的数据,可以得到a和话题D所在扇形的圆心角的度数;(4)根据题意和统计图中的数据,可以计算出计该小区居民中最关注的话题是“民法典”的人数大约有多少.
解:(1)200 (2)如图 (3)25,36
(4)10000×30%=3000(人),
答:该小区居民中最关注的话题是“民法典”的人数大约有3000人.
(1)调查的居民共有:60÷30%=200(人),
(2)选C的有:200×15%=30(人),选A的有:200﹣60﹣30﹣20﹣40=50(人),
(3)a%=50÷200×100%=25%,话题D所在扇形的圆心角是:360°×=36°,
(4)10000×30%=3000(人),
答:该小区居民中最关注的话题是“民法典”的人数大约有3000人.
【点评】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
【考点】坐标与图形变化-平移
【分析】(1)根据C、D两点在坐标系中的位置即可得出此两点坐标;
(2)先判断出四边形ABCD是平行四边形,再求出其面积即可;
(3)过点P作PQ∥AB,故可得出CD∥PQ,AB∥PQ,由平形线的性质即可得出结论.
解:(1)由图可知,C(4,2),D(0,2).
故答案为:(4,2),(0,2);
(2)∵线段CD由线段BA平移而成,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴S平行四边形ABCD=4×2=8.
故答案为:8;
(3)证明:如图,过点P作PQ∥AB,
∵CD∥AB,
∴CD∥PQ,AB∥PQ,
∴∠CDP=∠1,∠BOP=∠2,
∴∠CDP+∠BOP=∠1+∠2=∠OPD.
【点评】本题考查的是作图﹣平移变换,熟知图形平移的性质是解答此题的关键.
【考点】一次函数的应用
【分析】(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由待定系数法根据图象就可以求出解析式。
(2)先根据函数图象求出甲乙的速度,然后与追击问题就可以求出小亮追上小明的时间,就可以求出小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式。
(3)先根据相遇问题建立方程就可以求出a值,10分钟甲、乙走的路程就是相距的距离,14分钟小明走的路程和小亮追到小明时的时间就可以补充完图象。
解:(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由图象,得
,
解得:,
∴y1=﹣200x+2000;
(2)由题意,得
小明的速度为:2000÷40=50米/分,
小亮的速度为:2000÷10=200米/分,
∴小亮从甲地追上小明的时间为24×50÷(200﹣50)=8分钟,
∴24分钟时两人的距离为:S=24×50=1200,32分钟时S=0,
设S与x之间的函数关系式为:S=kx+b,由题意,得
,
解得:,
∴S=﹣150x+4800;
(3)由题意,得
a=2000÷(200+50)=8分钟,
当x=24时,S=1200
当x=32时,S=0.
故描出相应的点就可以补全图象.
如图:
【点评】本题时一道一次函数的综合试题,考查了待定系数法求一次函数的解析式的运用,追击问题与相遇问题在实际问题中的运用,描点法画函数图象的运用,解答时灵活运用路程、速度、时间之间的数量关系是关键.
【考点】全等三角形的证明,勾股定理的运用
【分析】如图,易证△ABC≌△CDE,得AB2+DE2=DE2+CD2=CE2,同理FG2+LK2=HL2,S1+S2+S3+S4=1+3=4.
解:
∵依次摆放着七个正方形,
∴EC=AC,∠EDC=∠ABC=∠ECA=90°,
∴∠ECD+∠ACB=90°,∠ECD+∠DEC=90°,
∴∠ECD=∠CAB,∠ACB=∠CED,
在△ABC和△CDE中,
∵
∴△ABC≌△CDE,
∴AB=CD,BC=DE,
∴AB2+DE2=DE2+CD2=CE2=3,
同理可证FG2+LK2=HL2=1,
∴S1+S2+S3+S4=CE2+HL2=1+3=4.
故答案为:4.
【点睛】本题考查全等三角形的证明,考查了勾股定理的灵活运用,本题中证明AB2+DE2=DE2+CD2=CE2是解题关键.
【考点】一次函数综合题
【分析】(1)先求出直线AD的解析式,再求得B点的纵坐标,再代入求得直线BC的解析式;
(2)根据一次函数的增减性,并结合函数图象可以求得不等式的解集;
(3)分三种情况分别求出△ABC的面积函数关系式.
解:(1)由题意得:直线AD过点A(0,4),D(4,0),直线AD为y1=k1x+b1
∴
解得:.
∴直线AD的解析式为y1=?x+4
又因为点B在AD上,且B点的横坐标为a=1,所以纵坐标为3,即B(1,3)
由题意的直线BC过点B(1,3),C(?2,0),直线BC为y2=k2x+b2
∴
解得:.
∴直线BC的解析式为y2=x+2
(2)因为直线AD与直线BC相交于点B(1,3)
由图象得:k1x+b1>k2x+b2时x的取值范围为x<1.
(3)△ABC的面积计算有三种形式,分别为点B在点A上方、在AD中间、在点D下方.
①点B在点A上方,即a≤0时:S△ABC=S△BCO+S△BAO?S△ACO
∴S=×2×(?a+4)+×4×(?a)? ×2×4=?3a
②当点B在点A和点D中间,即0<a<4时,:S△ABC=S△ACD?S△BCD
∴S=×6×4? ×6×(?a+4)=3a
③当点B在点D下方,即a≥4时,:S△ABC=S△ACD+S△BCD
∴S=×6×4+×6×(?(?a+4))=3a
综上所述得:S=
当直线CB把△ACD的面积分为1:2两部分时,即B点在点A和点D中间时.
此时S△ABC=3a,S△ACD=12.
当S△ABC:S△ACD=1:3时,即3a:12=1:3,
∴a=;
当S△ABC:S△ACD=2:3时,即3a:12=2:3,
∴a=.
【点睛】本题是一次函数的综合应用.综合性较强,注意第(3)题分三种情况分别求出△ABC的面积函数关系式.
_21?????????è?????(www.21cnjy.com)_
湘教教版八年级下期末模拟试卷2
姓名:__________班级:__________考号:__________总分__________
、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
在平面直角坐标系中,点P在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
在学习《图形变化的简单应用》这一节时,老师要求同学们利用图形变化设计图案.下列设计的图案中,是中心对称图形但不是轴对称图形的是( )
A. B. C. D.
如图,小红想用一条彩带缠绕易拉罐,正好从A点绕到正上方B点共四圈,已知易拉罐底面周长是12cm,高是20cm,那么所需彩带最短的是( )
A.13cm B.4cm C.4cm D.52cm
菱形,矩形,正方形都具有的性质是( )
A.对角线相等且互相平分 B.对角线相等且互相垂直平分
C.对角线互相平分 D.四条边相等,四个角相等
某地区用电量与应缴电费之间的关系如表:
用电量(千瓦·时) 1 2 3 4 …
应缴电费(元) 0.55 1.10 1.65 2.20 …
则下列叙述错误的是( )
A.若所缴电费为2.75元,则用电量为6千瓦·时
B.若用电量为8千瓦·时,则应缴电费4.4元
C.用电量每增加1千瓦·时,电费增加0.55元
D.所缴电费随用电量的增加而增加
正比例函数y=﹣3x的大致图象是( )
为了描述我国近年来GDP(国内生产总值)的变化趋势,选用的统计图最好是( )
A.条形统计图 B.折线统计图 C.扇形统计图 D.直方图
如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开.若测得 AM的长为1.2km,则M,C两点间的距离为(?? )
A.0.5 km????B.0.6 km????C.0.9 km?????D.1.2 km
平面直角坐标系中,点A(-3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的长度最小时点C的坐标为( )
A. B. C. D.
在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
A.∠ADE=20° B.∠ADE=30° C.∠ADE=∠ADC D.∠ADE=∠ADC
如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的动点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A. B. C. D.
x为任意实数,令F(x)表示{2x+1,x+2,﹣x+6}中的最小值,则F(x)的最大值是( )
A.0 B.2 C.4 D.6
、填空题(本大题共6小题,每小题3分,共18分)
八边形的内角和为 .
如图,△ABC中,∠A=∠ABC,AC=6,BD⊥AC于点D,E为BC的中点,连接DE.则DE=____________.
气象局要统计一昼夜气温变化情况,应选用___统计图.
函数中,自变量的取值范围是_____.
在平面直角坐标系中,点A是y轴上一点,若它的坐标为(a﹣1,a+1),另一点B的坐标为(a+3,a﹣5),则点B的坐标是 .
如图,边长为2a的正方形EFGH在边长为6a的正方形ABCD所在平面上移动,始终保持EF∥AB,线段CF的中点为M,DH的中点为N,则线段MN的长为 .
、解答题(本大题共8小题,共66分)
正方形的边长为2,建立适当的直角坐标系,使它的一个顶点的坐标为(,0),并写出另外三个顶点的坐标.
如图,在中,,点在上,若,平分.
(1)求的长;
(2)若是中点,求线段的长.
已知:如图,正比例函数y=kx的图象经过点A,
(1)请你求出该正比例函数的解析式;
(2)若这个函数的图象还经过点B(m,m+3),请你求出m的值;
(3)请你判断点P(﹣,1)是否在这个函数的图象上,为什么?
某校数学实践小组就近期人们比较关注的五个话题:“A.5G通讯;
B.民法典;C.北斗导航;D.数字经济; E.小康社会”,对某小区居民进行了随机抽样调查,每人只能从中选择一个本人最关注的话题,根据调查结果绘制了如图两幅不完整的统计图.
请结合统计图中的信息,解决下列问题:
(1)数学实践小组在这次活动中,调查的居民共有 人;
(2)将上面的最关注话题条形统计图补充完整;
(3)最关注话题扇形统计图中的a= ,话题D所在扇形的圆心角是 度;
(4)假设这个小区居民共有10000人,请估计该小区居民中最关注的话题是“民法典”的人数大约有多少?
如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.
(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路ι步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.
(1)求小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式;
(2)求小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
(3)在图2中,补全整个过程中s(米)与x(分钟)之间的函数图象,并确定a的值.
如图,已知斜放着的3个正方形面积分别为1,2,3,正放着的4个正方形的面积依次为S1,S2,S3,S4,求S1+S2+S3+S4的值.
如图,直线AD:y1=k1x+b1过点A(0,4),D(4,0),直线BC:y2=k2x+b2过点C(﹣2,0),且与直线AD交于点B,且点B的横坐标为a.
(1)当a=1时,求直线BC的解析式;
(2)在(1)的条件下,请直接写出k1x+b1>k2x+b2时,对应的x的取值范围;
(3)设的面积为S,用含a的代数式表示S,并求出当直线CB把的面积分为1:2的两部分时,对应a的值.
答案解析
、选择题
【考点】点的坐标.
【分析】点P的横、纵坐标均为正,可确定在第一象限.
解:点P的横、纵坐标均为正,所以点P在第一象限,故选A.
【点评】本题主要考查了平面直角坐标系中第二象限的点的坐标的符号特点.四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
【考点】中心对称图形,轴对称图形
【分析】根据轴对称图形与中心对称图形的概念求解.
解:A.是轴对称图形,不是中心对称图形,故此选项错误;
B、是轴对称图形,也是中心对称图形,故此选项错误;
C、不是轴对称图形,是中心对称图形,故此选项正确;
D、是轴对称图形,也是中心对称图形,故此选项错误.
故选:C.
【点评】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.
【考点】平面展开﹣最短路径问题.
【分析】要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理.
解:由图可知,彩带从易拉罐底端的A处绕易拉罐4圈后到达顶端的B处,将易拉罐表面切开展开呈长方形,则螺旋线长为四个长方形并排后的长方形的对角线长,
∵易拉罐底面周长是12cm,高是20cm,
∴x2=(12×4)2+202,
所以彩带最短是52cm.
故选D
【点评】本题考查了平面展开-最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.
【考点】正方形的性质;菱形的性质;矩形的性质.
【分析】对菱形对角线相互垂直平分,矩形对角线平分相等,正方形对角线相互垂直平分相等的性质进行分析从而得到其共有的性质.
解:A.不正确,菱形的对角线不相等;
B、不正确,菱形的对角线不相等,矩形的对角线不垂直;
C、正确,三者均具有此性质;
D、不正确,矩形的四边不相等,菱形的四个角不相等;
故选C.
【点评】熟练掌握菱形,矩形,正方形都具有的性质是解决本题的关键.
【考点】用表格表示变量之间的关系
【分析】电量从1千瓦·时到2千瓦·时,电费增加了1.1-0.55=0.55元,从2千瓦·时到3千瓦·时,电费增加了1.65-1.1=0.55元,从3千瓦·时到4千瓦·时,电费增加了2.20-1.65=0.55元,故用电量每增加1千瓦·时,电费增加0.55元,据此可回答问题.
解:A. 若所缴电费为2.75元时,电费为2.75÷0.55=5千瓦·时,故本选项错误;
B. 若用电量为8千瓦·时,电费为8×0.55=4.4元,故本选项正确;
C. 用电量每增加1千瓦·时,电费增加0.55元,故本选项正确;
D. 随着用电量增加,电费在逐渐增长,故本选项正确.
所以选A.
【点评】本题考查用表格表示变量之间的关系,解决本类题的关键是要观察表格,因变量是如何随着自变量改变的.
【考点】正比例函数的图象
【分析】正比例函数图象是经过原点的一条直线,根据y=kx中k的符号确定其所经过的象限.
解:正比例函数y=﹣3x的图象是经过原点的一条直线.
∵﹣3<0,
∴该直线经过第二、四象限.
观察选项,只有C选项符合条件.
故选:C.
【点评】考查了正比例函数的图象,正比例函数y=kx的图象是直线,当k>0时,直线经过第一、三象限;当k<0时,直线经过第二、四象限.
【考点】统计图的选择
【分析】根据统计图的特点进行选择:扇形统计图表示的是部分在总体中所占的百分比;折线统计图表示的是事物的变化情况;而条形统计图和直方图能清楚地表示出每个项目的具体数目;直方图能够清楚地表示出每组的具体数目,分组的时候,数据是连续的.
解:为了描述我国近年来GDP(国内生产总值)的变化趋势,选用的统计图最好是折线统计图.
所以B选项是正确的.
【点睛】本题考查了统计图的选择,属于简单题,熟悉统计图的特点是解题关键.
【考点】直角三角形斜边上的中线
【分析】根据直角三角形斜边的中线等于斜边的一半即可解决问题.
解:在Rt△ACB中, ∵∠ACB=90°,AM=BM,
∴CM= AB=AM,
∵AM=1.2km,
∴CM=1.2km,
故选D.
【点评】本题考查直角三角形的性质,解题的关键是掌握直角三角形斜边的中线等于斜边的一半的应用,属于中考常考题型.
【考点】坐标与图形的性质,垂线段的性质
【分析】由AC∥x轴,可得点C与点A的纵坐标相同,再根据垂线段最短可知BC⊥AC时,BC有最小值,从而可确定点C的坐标.
解:如图所示:
由垂线段最短可知:当BC⊥AC时,BC有最小值.
所以点C的坐标为(3,2),线段的最小值为2.
故选B.
【点睛】本题主要考查的是两点间的距离公式、垂线段的性质、点的坐标的定义,掌握垂线段的性质是解题的关键.
【考点】多边形内角与外角;三角形内角和定理.
【分析】利用三角形的内角和为180°,四边形的内角和为360°,分别表示出∠A,∠B,∠C,根据∠A=∠B=∠C,得到∠ADE=∠EDC,因为∠ADC=∠ADE+∠EDC=∠EDC+∠EDC=∠EDC,所以∠ADE=∠ADC,即可解答.
解:如图,
在△AED中,∠AED=60°,
∴∠A=180°﹣∠AED﹣∠ADE=120°﹣∠ADE,
在四边形DEBC中,∠DEB=180°﹣∠AED=180°﹣60°=120°,
∴∠B=∠C=(360°﹣∠DEB﹣∠EDC)÷2=120°﹣∠EDC,
∵∠A=∠B=∠C,
∴120°﹣∠ADE=120°﹣∠EDC,
∴∠ADE=∠EDC,
∵∠ADC=∠ADE+∠EDC=∠EDC+∠EDC=∠EDC,
∴∠ADE=∠ADC,
故选:D.
【点评】本题考查了多边形的内角和,解决本题的关键是熟记四边形的内角和为360°.
【考点】菱形的性质,轴对称-最短路线问题
【分析】作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP=NQ最小,NQ为所求,当NQ⊥AB时,NQ最小,继而利用面积法求出NQ长即可得答案.
解:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP=NQ最小,NQ为所求,当NQ⊥AB时,NQ最小,
∵四边形ABCD是菱形,AC=6,DB=8,
∴OA=3,OB=4,AC⊥BD,
在Rt△AOB中,AB==5,
∵S菱形ABCD=,
∴,
∴NQ=,
∴PM+PN的最小值为,
故选D.
【点睛】本题考查了菱形的性质,轴对称确定最短路线问题,熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键.
【考点】一次函数综合应用以及一次函数增减
【分析】根据已知设y1=2x+1,y2=x+2,y3=﹣x+6,进而求出图象交点坐标,进而得出此时的最值,最后比较得出答案.
解:设y1=2x+1,y2=x+2,y3=﹣x+6,
∵2x+1=x+2,
解得:x=1,则y=3,
∴y1,y2,交于(1,3),
∵x+2=﹣x+6,
解得:x=2,则y=4,
∴y2,y3交于(2,4),
∵2x+1=﹣x+6,
解得:x=,则y=,
∴y1,y3交于(,),
根据图象当x<1,F(x)=y1,此时函数的最值小于3,
当1≤x<,F(x)=y2,此时函数的最值小于,
当x≥2,F(x)=y3,此时函数的最值小于等于4,
故F(x)的最大值是4.
故选;C.
【点评】此题主要考查了一次函数综合应用以及一次函数增减性,利用数形结合得出是解题关键.
、填空题
【考点】多边形内角与外角.
【分析】根据多边形的内角和公式(n﹣2)?180°进行计算即可得解.
解:(8﹣2)?180°=6×180°=1080°.
故答案为:1080°.
【点评】本题考查了多边形的内角和,熟记内角和公式是解题的关键.
【考点】直角三角形斜边上的中线,等腰三角形的判定与性质
【分析】利用等腰三角形的判定与性质求出CA=CB=6,再利用直角三角形斜边上的中线求出BC=2DE,得出DE
解:∵∠A=∠ABC,
∴CA=CB,
∵BD⊥AC,
∴∠BDC=90°.
∵E为CB的中点,
∴BC=2DE,
∴6=2DE,
则DE=3.
故本题应填3.
【点评】直角三角形斜边上的中线,等腰三角形的判定与性质,熟练掌握各性质定理是解题的关键
【考点】统计图的选择
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可.
解:因为折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况,
所以要统计一昼夜气温变化情况,应选用折线统计图;
故答案为:折线.
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答.
【考点】函数自变量的取值范围
【分析】根据被开方式是非负数列式求解即可.
解:依题意,得,
解得:,
故答案为.
【点睛】本题考查了函数自变量的取值范围,函数有意义时字母的取值范围一般从几个方面考虑:①当函数解析式是整式时,字母可取全体实数;②当函数解析式是分式时,考虑分式的分母不能为0;③当函数解析式是二次根式时,被开方数为非负数.④对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.
【考点】点的坐标.
【分析】点在y轴上,则其横坐标是0.
解:∵点A(a﹣1,a+1)是y轴上一点,
∴a﹣1=0,
解得a=1,
∴a+3=1+3=4,a﹣5=1﹣5=﹣4,
∴点B的坐标是(4,﹣4).故答案填:(4,﹣4).
【点评】本题考查了坐标轴上的点的坐标的特征:点在y轴上时,其横坐标是0.
【考点】三角形中位线定理;全等三角形的判定与性质;勾股定理;正方形的性质.
【分析】因为题目没有确定正方形EFGH的位置,所以我们可以将正方形EFGH的位置特殊化,使点H与点A重合,重新作出图形,这样有利于我们解题,过点M作MO⊥ED与O,则可得出OM是梯形FEDC的中位线,从而可求出ON、OM,然后在RT△MON中利用勾股定理可求出MN.
解:如图,将正方形EFGH的位置特殊化,使点H与点A重合,过点M作MO⊥ED与O,则MO是梯形FEDC的中位线,
∴EO=OD=4a,MO=(EF+CD)=4a.
∵点N、M分别是AD、FC的中点,
∴AN=ND=3a,
∴ON=OD﹣ND=4a﹣3a=a.
在Rt△MON中,MN2=MO2+ON2,即MN===a.
故答案是: a.
【点评】本题考查了梯形的中位线定理、正方形的性质及勾股定理的知识,属于综合性题目,对待这样既有动态因素又不确定位置的题目,一定要将位置特殊化,这样不影响结果且解题过程简单,同学们要学会在以后的解题中利用这种思想.
、解答题
【考点】正方形的性质;坐标与图形性质.
【分析】先找到A(,0),根据正方形的对称性,可知A点的对称点C的坐标,同样可得出B和D的坐标.
解:建立坐标轴,使正方形的对称中心为原点,
则A(,0),C(﹣,0),
那么B的坐标是(0,),
其对称点D的坐标是(0,﹣).
【点评】本题利用了正方形既是轴对称图形又是中心对称图形的性质.
【考点】三角形中位线定理,等边三角形的性质
【分析】(1)先证明△ABD是等腰三角形,再根据三线合一得到,利用勾股定理求得AE的长;
(2)利用三角线的中位线定理可得:,再进行求解.
解:(1)
∴
∵平分,
∴
根据勾股定理,得
(2)由(1),知,
又∵,
∴.
【点睛】考查了三角形中位线定理,解题关键是利用三线合一和三角形的中位线.
【考点】一次函数图象上点的坐标特征;待定系数法求正比例函数解析式
【分析】(1)将点A(﹣1,2)代入y=kx求得k的值即可得;
(2)将点B坐标代入函数解析式可得m的方程,解之即可得;
(3)在所求函数解析式中求出x=﹣时y的值,看是否等于1即可得出结论.
解:(1)由图可知点A(﹣1,2),代入y=kx得:
﹣k=2,k=﹣2,
则正比例函数解析式为y=﹣2x;
(2)将点B(m,m+3)代入y=﹣2x,得:﹣2m=m+3,
解得:m=﹣1;
(3)当x=﹣时,y=﹣2×(﹣)=3≠1,
所以点P不在这个函数图象上.
【点评】本题主要考查待定系数法求出一次函数解析式,解题的关键是熟练掌握待定系数法求函数解析式及一次函数图象上点的坐标特征.
【考点】条形统计图,扇形统计图,用样本估计总体
【分析】(1)根据选择B的人数和所占的百分比,可以求得本次调查的居民人数;(2)根据(1)中的结果和统计图中的数据,可以计算出选择A和C的人数,从而可以将条形统计图补充完整;(3)根据统计图中的数据,可以得到a和话题D所在扇形的圆心角的度数;(4)根据题意和统计图中的数据,可以计算出计该小区居民中最关注的话题是“民法典”的人数大约有多少.
解:(1)200 (2)如图 (3)25,36
(4)10000×30%=3000(人),
答:该小区居民中最关注的话题是“民法典”的人数大约有3000人.
(1)调查的居民共有:60÷30%=200(人),
(2)选C的有:200×15%=30(人),选A的有:200﹣60﹣30﹣20﹣40=50(人),
(3)a%=50÷200×100%=25%,话题D所在扇形的圆心角是:360°×=36°,
(4)10000×30%=3000(人),
答:该小区居民中最关注的话题是“民法典”的人数大约有3000人.
【点评】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
【考点】坐标与图形变化-平移
【分析】(1)根据C、D两点在坐标系中的位置即可得出此两点坐标;
(2)先判断出四边形ABCD是平行四边形,再求出其面积即可;
(3)过点P作PQ∥AB,故可得出CD∥PQ,AB∥PQ,由平形线的性质即可得出结论.
解:(1)由图可知,C(4,2),D(0,2).
故答案为:(4,2),(0,2);
(2)∵线段CD由线段BA平移而成,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴S平行四边形ABCD=4×2=8.
故答案为:8;
(3)证明:如图,过点P作PQ∥AB,
∵CD∥AB,
∴CD∥PQ,AB∥PQ,
∴∠CDP=∠1,∠BOP=∠2,
∴∠CDP+∠BOP=∠1+∠2=∠OPD.
【点评】本题考查的是作图﹣平移变换,熟知图形平移的性质是解答此题的关键.
【考点】一次函数的应用
【分析】(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由待定系数法根据图象就可以求出解析式。
(2)先根据函数图象求出甲乙的速度,然后与追击问题就可以求出小亮追上小明的时间,就可以求出小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式。
(3)先根据相遇问题建立方程就可以求出a值,10分钟甲、乙走的路程就是相距的距离,14分钟小明走的路程和小亮追到小明时的时间就可以补充完图象。
解:(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由图象,得
,
解得:,
∴y1=﹣200x+2000;
(2)由题意,得
小明的速度为:2000÷40=50米/分,
小亮的速度为:2000÷10=200米/分,
∴小亮从甲地追上小明的时间为24×50÷(200﹣50)=8分钟,
∴24分钟时两人的距离为:S=24×50=1200,32分钟时S=0,
设S与x之间的函数关系式为:S=kx+b,由题意,得
,
解得:,
∴S=﹣150x+4800;
(3)由题意,得
a=2000÷(200+50)=8分钟,
当x=24时,S=1200
当x=32时,S=0.
故描出相应的点就可以补全图象.
如图:
【点评】本题时一道一次函数的综合试题,考查了待定系数法求一次函数的解析式的运用,追击问题与相遇问题在实际问题中的运用,描点法画函数图象的运用,解答时灵活运用路程、速度、时间之间的数量关系是关键.
【考点】全等三角形的证明,勾股定理的运用
【分析】如图,易证△ABC≌△CDE,得AB2+DE2=DE2+CD2=CE2,同理FG2+LK2=HL2,S1+S2+S3+S4=1+3=4.
解:
∵依次摆放着七个正方形,
∴EC=AC,∠EDC=∠ABC=∠ECA=90°,
∴∠ECD+∠ACB=90°,∠ECD+∠DEC=90°,
∴∠ECD=∠CAB,∠ACB=∠CED,
在△ABC和△CDE中,
∵
∴△ABC≌△CDE,
∴AB=CD,BC=DE,
∴AB2+DE2=DE2+CD2=CE2=3,
同理可证FG2+LK2=HL2=1,
∴S1+S2+S3+S4=CE2+HL2=1+3=4.
故答案为:4.
【点睛】本题考查全等三角形的证明,考查了勾股定理的灵活运用,本题中证明AB2+DE2=DE2+CD2=CE2是解题关键.
【考点】一次函数综合题
【分析】(1)先求出直线AD的解析式,再求得B点的纵坐标,再代入求得直线BC的解析式;
(2)根据一次函数的增减性,并结合函数图象可以求得不等式的解集;
(3)分三种情况分别求出△ABC的面积函数关系式.
解:(1)由题意得:直线AD过点A(0,4),D(4,0),直线AD为y1=k1x+b1
∴
解得:.
∴直线AD的解析式为y1=?x+4
又因为点B在AD上,且B点的横坐标为a=1,所以纵坐标为3,即B(1,3)
由题意的直线BC过点B(1,3),C(?2,0),直线BC为y2=k2x+b2
∴
解得:.
∴直线BC的解析式为y2=x+2
(2)因为直线AD与直线BC相交于点B(1,3)
由图象得:k1x+b1>k2x+b2时x的取值范围为x<1.
(3)△ABC的面积计算有三种形式,分别为点B在点A上方、在AD中间、在点D下方.
①点B在点A上方,即a≤0时:S△ABC=S△BCO+S△BAO?S△ACO
∴S=×2×(?a+4)+×4×(?a)? ×2×4=?3a
②当点B在点A和点D中间,即0<a<4时,:S△ABC=S△ACD?S△BCD
∴S=×6×4? ×6×(?a+4)=3a
③当点B在点D下方,即a≥4时,:S△ABC=S△ACD+S△BCD
∴S=×6×4+×6×(?(?a+4))=3a
综上所述得:S=
当直线CB把△ACD的面积分为1:2两部分时,即B点在点A和点D中间时.
此时S△ABC=3a,S△ACD=12.
当S△ABC:S△ACD=1:3时,即3a:12=1:3,
∴a=;
当S△ABC:S△ACD=2:3时,即3a:12=2:3,
∴a=.
【点睛】本题是一次函数的综合应用.综合性较强,注意第(3)题分三种情况分别求出△ABC的面积函数关系式.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
