第九章《统计》单元检测卷B - 2020-2021学年高一下学期数学人教A版(2019)必修第二册(Word含答案解析)
文档属性
| 名称 | 第九章《统计》单元检测卷B - 2020-2021学年高一下学期数学人教A版(2019)必修第二册(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 679.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 00:00:00 | ||
图片预览




文档简介
第九章《统计》
单元检测卷B
一.单项选择题:本大题共4小题,每小题7分,共28分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)《高中数学课程标准》(版)规定了数学直观想象学科的六大核心素养,为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是 (注:雷达图,又可称为戴布拉图、蜘蛛网图,可用于对研究对象的多维分析)
A.甲的数据分析素养高于乙
B.甲的数学建模素养优于数学抽象素养
C.乙的六大素养中逻辑推理最差
D.乙的六大素养整体水平优于甲
(2)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该 折线图,下列结论正确的是
A.月接待游客逐月增加
B.年接待游客量逐年减少
C.各年的月接待游客量高峰期大致在6、7月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性较小,变化比较稳定
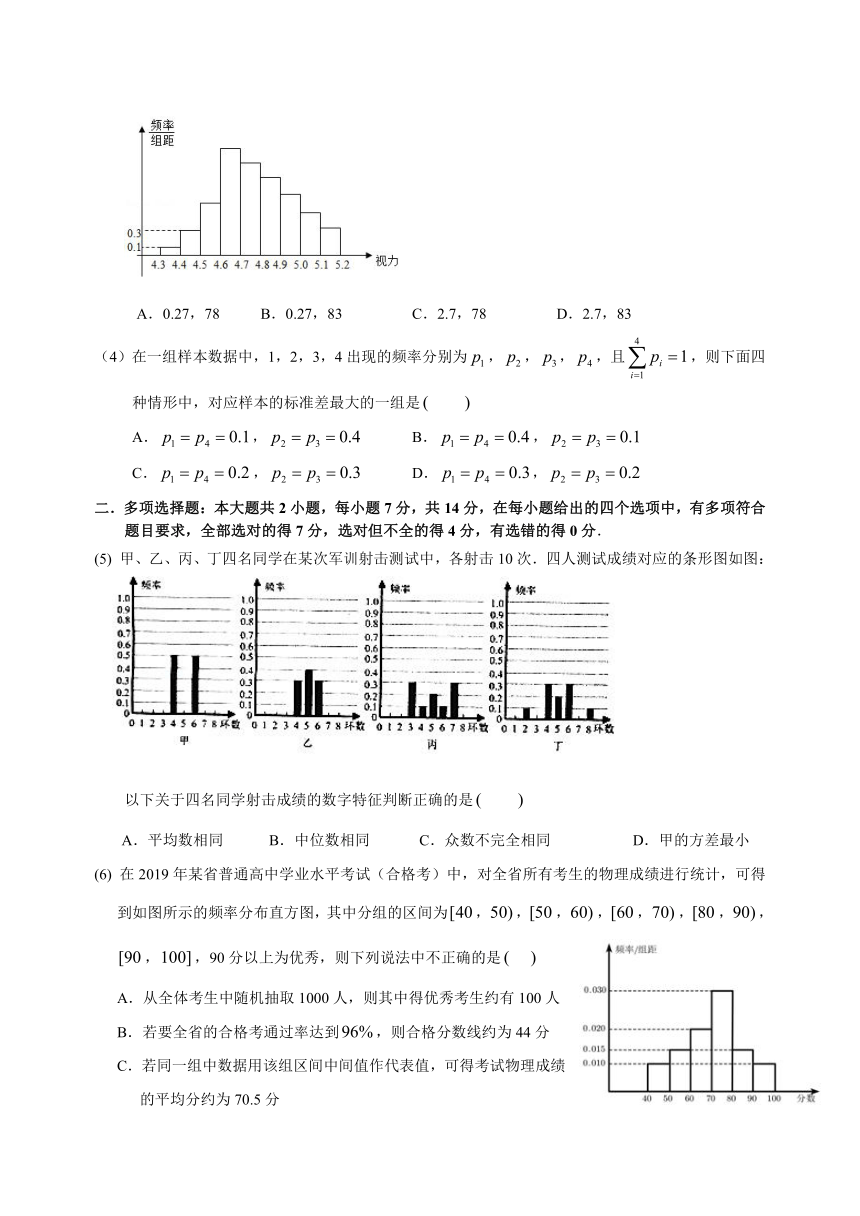
(3)为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,但知道前4组的频数分别是,,,,且满足,后6组的频数为,,,,满足,设最大频率为,视力在4.6到5.0之间的学生数为,则,的值分别为
A.0.27,78 B.0.27,83 C.2.7,78 D.2.7,83
(4)在一组样本数据中,1,2,3,4出现的频率分别为,,,,且,则下面四种情形中,对应样本的标准差最大的一组是
A., B.,
C., D.,
二.多项选择题:本大题共2小题,每小题7分,共14分,在每小题给出的四个选项中,有多项符合题目要求,全部选对的得7分,选对但不全的得4分,有选错的得0分.
(5) 甲、乙、丙、丁四名同学在某次军训射击测试中,各射击10次.四人测试成绩对应的条形图如图:
以下关于四名同学射击成绩的数字特征判断正确的是
A.平均数相同 B.中位数相同 C.众数不完全相同 D.甲的方差最小
(6) 在2019年某省普通高中学业水平考试(合格考)中,对全省所有考生的物理成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为,,,,,,,,,,90分以上为优秀,则下列说法中不正确的是
A.从全体考生中随机抽取1000人,则其中得优秀考生约有100人
B.若要全省的合格考通过率达到,则合格分数线约为44分
C.若同一组中数据用该组区间中间值作代表值,可得考试物理成绩
的平均分约为70.5分
D.该省考生物理成绩的中位数为75分
三、填空题:本大题共4题,每小题7分,共28分.
(7) 某市新上了一批便民公共自行车,有绿色和橙黄色两种颜色,且绿色公共自行车和橙黄色公共自行车的数量比为,现在按照分层抽样的方法抽取36辆这样的公共自行车放在某校门口,则其中绿色公共自行车的辆数是 .
(8) 从某工厂生产线上随机抽取16件零件,测量其内径数据从小到大依次排列如下(单位:,1.15,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42.据此可估计该生产线上大约有的零件内径小于等于 ,大约有的零件内径大于 .
(9) 已知样本,,,的平均数为;样本,,,的平均数为,若样本,,,,,,,的平均数;其中,则,的大小关系为 .
(10)在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各个选项中,一定符合上述指标的是 .
①平均数;②标准差;③平均数且标准差;
④平均数且极差小于或等于2;⑤众数等于1且极差小于或等于4.
四、解答题:本大题共3小题,共30分,解答应写出文字说明,证明过程或演算步骤.
(11)(本小题满分8分)
为了解某小区7月用电量情况,通过抽样,获得了100户居民7月用电量(单位:度),将数据按照,,,,,,分成六组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中的值;
(2)已知该小区有1000户居民,估计该小区7月用电量不低于200度的户数,并说明理由;
(3)估计该小区的居民7月用电量的值,并说明理由.
(12)(本小题满分10分)
小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(1)请分别求出甲、乙两种薪酬方案中日薪(单位:元)与送货单数的函数关系式;
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数与天数满足以下表格:
日均派送单数 52 54 56 58 60
频数(天 20 30 20 20 10
回答下列问题:
①根据以上数据,设每名派送员的日薪为(单位:元),试分别求出这100天中甲、乙两种方案的日薪平均数及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据:,,,,,,,,
(13)(本小题满分12分)
某玻璃工艺品加工厂有2条生产线用于生产某款产品,每条生产线一天能生产200件该产品,该产品市场评级规定:评分在10分及以上的为等品,低于10分的为等品.厂家将等品售价定为2000元件,等品售价定为1200元件.
下面是检验员在现有生产线上随机抽取的16件产品的评分:
9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得,,其中为抽取的第件产品的评分,,2,,16.
该厂计划通过增加生产工序来改进生产工艺,已知对一条生产线增加生产工序每年需花费1500万元,改进后该条生产线产能不变,但生产出的每件产品评分均提高0.05.已知该厂现有一笔1500万元的资金.
(1)若厂家用这1500万元改进一条生产线,根据随机抽取的16件产品的评分,
估计改进后该生产线生产的产品中等品所占的比例;
估计改进后该厂生产的所有产品评分的平均数和方差.
(2)某金融机构向该厂推销一款年收益率为的理财产品.请你利用所学知识分析,将这1500万元用于购买该款理财产品所获得的收益,与通过改进一条生产线使产品评分提高所增加的收益相对比,一年后哪种方案的收益更大?(一年按365天计算)
2023届漳州市高一下数学第九章《统计》
单元检测卷B参考答案
一.单项选择题:本大题共4小题,每小题7分,共28分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)答案:D
【解析】对于A选项,甲的数据分析为3分,乙的数据分析为5分,即甲的数据分析素养低于乙,故选项A错误,
对于B选项,甲的数学建模素养为3分,数学抽象素养为3分,即甲的数学建模素养与数学抽象素养同一水平,故选项B错误,
对于C选项,由雷达图可知,乙的六大素养中数学建模、数学抽象、数学运算最差,故选项C错误,
对于D选项,乙的六大素养中只有数学运算比甲差,其余都由于甲,即乙的六大素养整体水平优于甲,故选项D正确,故选:D.
(2)答案:D
【解析】由已有中2014年1月至2016年12月期间月接待游客量(单位:万人)的数据可得:月接待游客量逐月有增有减,故A错误;年接待游客量逐年增加,故B错误;
各年的月接待游客量高峰期大致在7,8月,故C错误;各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D正确;故选:D.
(3)答案:A
【解析】由频率分布直方图知组矩为0.1,间的频数为.
间的频数为. 根据后6组频数,且共有人.
从而间的频数最大,且为,,设,
则.,从而.故选:A.
(4)答案:B
【解析】选项,
所以;
同理选项,;选项,;
选项,;故选:B.
二.多项选择题:本大题共2小题,每小题7分,共14分,在每小题给出的四个选项中,有多项符合题目要求,全部选对的得7分,选对但不全的得4分,有选错的得0分.
(5) 答案: ABC
【解析】由条形图知,甲射击成绩为:4,4,4,4,4,6,6,6,6,6;
所以甲的平均数是5,中位数是5,众数是4,6,方差是1;乙射击成绩为:4,4,4,5,5,5,5,6,6,6;乙的平均数是5,中位数是5,众数是5,方差是0.6;丙射击成绩为:3,3,3,4,5,5,6,7,7,7;丙的平均数是5,中位数是5,众数是3,7,方差是1.8;
丁射击成绩为:2,4,4,4,5,5,6,6,6,8;丁的平均数是5,中位数是5,众数是4,6,方差是2.4;所以它们的平均数相同,中位数相同,众数不完全相同,乙的方差最小.故选:ABC.
(6) 答案:BD
【解析】对于A,90分以上为优秀,由频率分布直方图得优秀的频率为,
所以从全体考生中随机抽取1000人,则其中得优秀考试生约有:人,故正确;对于B,由频率分布直方图得,的频率为,,的频率为:,所以若要全省的合格考通过率达到,则合格分数线约为44分,故正确;
对于C,若同一组中数据用该组区间中间值作代表值,可得考试物理成绩的平均分约为:
分,故C正确;对于D,,的频率为:,
,的频率为,所以该省考生物理成绩的中位数为:
分,故D错误.故选:BD.
三、填空题:本大题共4题,每小题7分,共28分.
(7) 答案:
【解析】根据题意,绿色公共自行车和橙黄色公共自行车的数量比为,所以样本中绿色公共自行车和橙黄色公共自行车的数量比也为,所以绿色公共自行车的辆数为,故答案为.
(8) 答案:,
【解析】从某工厂生产线上随机抽取16件零件,测量其内径数据从小到大依次排列如下(单位:1.12,1.15,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42.,,据此可估计该生产线上大约有的零件内径小于等于,大约有的零件内径大于.故答案为:,.
(9) 答案:
【解析】由样本,,,的平均数为,样本,,的平均数为,
样本,,,,,,的平均数,其中,
因为,所以,又时,,
所以 ,所以.
(10) 答案: ④⑤
【解析】①错.举反例:0,0,0,0,2,6,6;其平均数,不符合条件;
②错.举反倒:6,6,6,6,6,6,6;其标准差,不符合条件;
③错.举反倒:0,3,3,3,3,3,6;其平均数且标准差,不符合条件;
④对.若极差小于2,显然符合条件;若极差小于或等于2,有可能(1)0,1,2;(2)1,2,3;(3)2,3,4;(4)3,4,5;(5)4,5,6.在平均数的条件下,只有(1)(2)(3)成立,符合条件;⑤对.在众数等于1且极差小于或等于4时,其最大数不超过5,符合条件.
故答案为:④⑤.
四、解答题:本大题共3小题,共30分,解答应写出文字说明,证明过程或演算步骤.
(11)(本小题满分8分)
【解析】(1)由频率分布直方图可得:,解得:.
(2)由频率分布直方图可得,100户居民7月用电量不低于200度的频率为
,由此可以估计该小区有1000户居民7月用电量不低于200度
的户数为.
(3)由频率分布直方图可得,7月用电量低于250度的频率为0.82,7月用电量低于300度的频率为0.94,所以分位数一定位于区间内,由.由此估计该小区的居民7月用电量约为262.5度.
(12)(本小题满分10分)
【解析】(1)甲方案中派送员日薪(单位:元)与送货单数的函数关系式为:,,乙方案中派送员日薪(单位:元)与送单数的函数关系式为:
.
(2)①、由表格可知,甲方案中,日薪为152元的有20天,日薪为154元的有30天,
日薪为156元的有20天,日薪为158元的有20天,日薪为160元的有10天,
,
,
乙方案中,日薪为140元的有50天,日薪为152元的有20天,日薪为176元的有20天,日薪为200元的有10天,,
.
②答案一:
由以上的计算可知,虽然,但两者相差不大,且远小于,
即甲方案日工资收入波动相对较小,所以小明应选择甲方案.
答案二:
由以上的计算结果可以看出,,
即甲方案日工资期望小于乙方案日工资期望,所以小明应选择乙方案.
(13)(本小题满分12分)
【解析】(1)改进后,随机抽取的16件产品的评分依次变为:
10.00 10.17 10.01 10.01 10.06 9.97 10.03 10.09
10.31 9.96 10.18 10.07 9.27 10.09 10.10 10.00
其中,等品共有13个,
所以估计改进后该生产线生产的新产品中等品所占的比例为.
设一条生产线改进前一天生产出的产品评分为,2,3,,,
改进后该天生产出的产品评分设为,2,3,,,其中,
由已知得用样本估计总体可知,所以,所以估计改进一条生产线后该厂生产的所有产品评分的平均数为:.由已知得用样本估计总体可知,估计改进后该厂的所有产品评分的方差为:
,
,,
同理,,
式
.
(2)将这1500万元用于改进一条生产线,一年后因产品评分提高而增加的收益为:
(元,将这1500万元购买该款理财产品,一年后的收益为:(元,
,将这1500万元用于改进一条生产线一年后收益更大.
单元检测卷B
一.单项选择题:本大题共4小题,每小题7分,共28分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)《高中数学课程标准》(版)规定了数学直观想象学科的六大核心素养,为了比较甲、乙两名高二学生的数学核心素养水平,现以六大素养为指标对二人进行了测验,根据测验结果绘制了雷达图(如图,每项指标值满分为5分,分值高者为优),则下面叙述正确的是 (注:雷达图,又可称为戴布拉图、蜘蛛网图,可用于对研究对象的多维分析)
A.甲的数据分析素养高于乙
B.甲的数学建模素养优于数学抽象素养
C.乙的六大素养中逻辑推理最差
D.乙的六大素养整体水平优于甲
(2)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该 折线图,下列结论正确的是
A.月接待游客逐月增加
B.年接待游客量逐年减少
C.各年的月接待游客量高峰期大致在6、7月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性较小,变化比较稳定
(3)为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图,由于不慎将部分数据丢失,但知道前4组的频数分别是,,,,且满足,后6组的频数为,,,,满足,设最大频率为,视力在4.6到5.0之间的学生数为,则,的值分别为
A.0.27,78 B.0.27,83 C.2.7,78 D.2.7,83
(4)在一组样本数据中,1,2,3,4出现的频率分别为,,,,且,则下面四种情形中,对应样本的标准差最大的一组是
A., B.,
C., D.,
二.多项选择题:本大题共2小题,每小题7分,共14分,在每小题给出的四个选项中,有多项符合题目要求,全部选对的得7分,选对但不全的得4分,有选错的得0分.
(5) 甲、乙、丙、丁四名同学在某次军训射击测试中,各射击10次.四人测试成绩对应的条形图如图:
以下关于四名同学射击成绩的数字特征判断正确的是
A.平均数相同 B.中位数相同 C.众数不完全相同 D.甲的方差最小
(6) 在2019年某省普通高中学业水平考试(合格考)中,对全省所有考生的物理成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为,,,,,,,,,,90分以上为优秀,则下列说法中不正确的是
A.从全体考生中随机抽取1000人,则其中得优秀考生约有100人
B.若要全省的合格考通过率达到,则合格分数线约为44分
C.若同一组中数据用该组区间中间值作代表值,可得考试物理成绩
的平均分约为70.5分
D.该省考生物理成绩的中位数为75分
三、填空题:本大题共4题,每小题7分,共28分.
(7) 某市新上了一批便民公共自行车,有绿色和橙黄色两种颜色,且绿色公共自行车和橙黄色公共自行车的数量比为,现在按照分层抽样的方法抽取36辆这样的公共自行车放在某校门口,则其中绿色公共自行车的辆数是 .
(8) 从某工厂生产线上随机抽取16件零件,测量其内径数据从小到大依次排列如下(单位:,1.15,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42.据此可估计该生产线上大约有的零件内径小于等于 ,大约有的零件内径大于 .
(9) 已知样本,,,的平均数为;样本,,,的平均数为,若样本,,,,,,,的平均数;其中,则,的大小关系为 .
(10)在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各个选项中,一定符合上述指标的是 .
①平均数;②标准差;③平均数且标准差;
④平均数且极差小于或等于2;⑤众数等于1且极差小于或等于4.
四、解答题:本大题共3小题,共30分,解答应写出文字说明,证明过程或演算步骤.
(11)(本小题满分8分)
为了解某小区7月用电量情况,通过抽样,获得了100户居民7月用电量(单位:度),将数据按照,,,,,,分成六组,制成了如图所示的频率分布直方图.
(1)求频率分布直方图中的值;
(2)已知该小区有1000户居民,估计该小区7月用电量不低于200度的户数,并说明理由;
(3)估计该小区的居民7月用电量的值,并说明理由.
(12)(本小题满分10分)
小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(1)请分别求出甲、乙两种薪酬方案中日薪(单位:元)与送货单数的函数关系式;
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数与天数满足以下表格:
日均派送单数 52 54 56 58 60
频数(天 20 30 20 20 10
回答下列问题:
①根据以上数据,设每名派送员的日薪为(单位:元),试分别求出这100天中甲、乙两种方案的日薪平均数及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据:,,,,,,,,
(13)(本小题满分12分)
某玻璃工艺品加工厂有2条生产线用于生产某款产品,每条生产线一天能生产200件该产品,该产品市场评级规定:评分在10分及以上的为等品,低于10分的为等品.厂家将等品售价定为2000元件,等品售价定为1200元件.
下面是检验员在现有生产线上随机抽取的16件产品的评分:
9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得,,其中为抽取的第件产品的评分,,2,,16.
该厂计划通过增加生产工序来改进生产工艺,已知对一条生产线增加生产工序每年需花费1500万元,改进后该条生产线产能不变,但生产出的每件产品评分均提高0.05.已知该厂现有一笔1500万元的资金.
(1)若厂家用这1500万元改进一条生产线,根据随机抽取的16件产品的评分,
估计改进后该生产线生产的产品中等品所占的比例;
估计改进后该厂生产的所有产品评分的平均数和方差.
(2)某金融机构向该厂推销一款年收益率为的理财产品.请你利用所学知识分析,将这1500万元用于购买该款理财产品所获得的收益,与通过改进一条生产线使产品评分提高所增加的收益相对比,一年后哪种方案的收益更大?(一年按365天计算)
2023届漳州市高一下数学第九章《统计》
单元检测卷B参考答案
一.单项选择题:本大题共4小题,每小题7分,共28分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)答案:D
【解析】对于A选项,甲的数据分析为3分,乙的数据分析为5分,即甲的数据分析素养低于乙,故选项A错误,
对于B选项,甲的数学建模素养为3分,数学抽象素养为3分,即甲的数学建模素养与数学抽象素养同一水平,故选项B错误,
对于C选项,由雷达图可知,乙的六大素养中数学建模、数学抽象、数学运算最差,故选项C错误,
对于D选项,乙的六大素养中只有数学运算比甲差,其余都由于甲,即乙的六大素养整体水平优于甲,故选项D正确,故选:D.
(2)答案:D
【解析】由已有中2014年1月至2016年12月期间月接待游客量(单位:万人)的数据可得:月接待游客量逐月有增有减,故A错误;年接待游客量逐年增加,故B错误;
各年的月接待游客量高峰期大致在7,8月,故C错误;各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D正确;故选:D.
(3)答案:A
【解析】由频率分布直方图知组矩为0.1,间的频数为.
间的频数为. 根据后6组频数,且共有人.
从而间的频数最大,且为,,设,
则.,从而.故选:A.
(4)答案:B
【解析】选项,
所以;
同理选项,;选项,;
选项,;故选:B.
二.多项选择题:本大题共2小题,每小题7分,共14分,在每小题给出的四个选项中,有多项符合题目要求,全部选对的得7分,选对但不全的得4分,有选错的得0分.
(5) 答案: ABC
【解析】由条形图知,甲射击成绩为:4,4,4,4,4,6,6,6,6,6;
所以甲的平均数是5,中位数是5,众数是4,6,方差是1;乙射击成绩为:4,4,4,5,5,5,5,6,6,6;乙的平均数是5,中位数是5,众数是5,方差是0.6;丙射击成绩为:3,3,3,4,5,5,6,7,7,7;丙的平均数是5,中位数是5,众数是3,7,方差是1.8;
丁射击成绩为:2,4,4,4,5,5,6,6,6,8;丁的平均数是5,中位数是5,众数是4,6,方差是2.4;所以它们的平均数相同,中位数相同,众数不完全相同,乙的方差最小.故选:ABC.
(6) 答案:BD
【解析】对于A,90分以上为优秀,由频率分布直方图得优秀的频率为,
所以从全体考生中随机抽取1000人,则其中得优秀考试生约有:人,故正确;对于B,由频率分布直方图得,的频率为,,的频率为:,所以若要全省的合格考通过率达到,则合格分数线约为44分,故正确;
对于C,若同一组中数据用该组区间中间值作代表值,可得考试物理成绩的平均分约为:
分,故C正确;对于D,,的频率为:,
,的频率为,所以该省考生物理成绩的中位数为:
分,故D错误.故选:BD.
三、填空题:本大题共4题,每小题7分,共28分.
(7) 答案:
【解析】根据题意,绿色公共自行车和橙黄色公共自行车的数量比为,所以样本中绿色公共自行车和橙黄色公共自行车的数量比也为,所以绿色公共自行车的辆数为,故答案为.
(8) 答案:,
【解析】从某工厂生产线上随机抽取16件零件,测量其内径数据从小到大依次排列如下(单位:1.12,1.15,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42.,,据此可估计该生产线上大约有的零件内径小于等于,大约有的零件内径大于.故答案为:,.
(9) 答案:
【解析】由样本,,,的平均数为,样本,,的平均数为,
样本,,,,,,的平均数,其中,
因为,所以,又时,,
所以 ,所以.
(10) 答案: ④⑤
【解析】①错.举反例:0,0,0,0,2,6,6;其平均数,不符合条件;
②错.举反倒:6,6,6,6,6,6,6;其标准差,不符合条件;
③错.举反倒:0,3,3,3,3,3,6;其平均数且标准差,不符合条件;
④对.若极差小于2,显然符合条件;若极差小于或等于2,有可能(1)0,1,2;(2)1,2,3;(3)2,3,4;(4)3,4,5;(5)4,5,6.在平均数的条件下,只有(1)(2)(3)成立,符合条件;⑤对.在众数等于1且极差小于或等于4时,其最大数不超过5,符合条件.
故答案为:④⑤.
四、解答题:本大题共3小题,共30分,解答应写出文字说明,证明过程或演算步骤.
(11)(本小题满分8分)
【解析】(1)由频率分布直方图可得:,解得:.
(2)由频率分布直方图可得,100户居民7月用电量不低于200度的频率为
,由此可以估计该小区有1000户居民7月用电量不低于200度
的户数为.
(3)由频率分布直方图可得,7月用电量低于250度的频率为0.82,7月用电量低于300度的频率为0.94,所以分位数一定位于区间内,由.由此估计该小区的居民7月用电量约为262.5度.
(12)(本小题满分10分)
【解析】(1)甲方案中派送员日薪(单位:元)与送货单数的函数关系式为:,,乙方案中派送员日薪(单位:元)与送单数的函数关系式为:
.
(2)①、由表格可知,甲方案中,日薪为152元的有20天,日薪为154元的有30天,
日薪为156元的有20天,日薪为158元的有20天,日薪为160元的有10天,
,
,
乙方案中,日薪为140元的有50天,日薪为152元的有20天,日薪为176元的有20天,日薪为200元的有10天,,
.
②答案一:
由以上的计算可知,虽然,但两者相差不大,且远小于,
即甲方案日工资收入波动相对较小,所以小明应选择甲方案.
答案二:
由以上的计算结果可以看出,,
即甲方案日工资期望小于乙方案日工资期望,所以小明应选择乙方案.
(13)(本小题满分12分)
【解析】(1)改进后,随机抽取的16件产品的评分依次变为:
10.00 10.17 10.01 10.01 10.06 9.97 10.03 10.09
10.31 9.96 10.18 10.07 9.27 10.09 10.10 10.00
其中,等品共有13个,
所以估计改进后该生产线生产的新产品中等品所占的比例为.
设一条生产线改进前一天生产出的产品评分为,2,3,,,
改进后该天生产出的产品评分设为,2,3,,,其中,
由已知得用样本估计总体可知,所以,所以估计改进一条生产线后该厂生产的所有产品评分的平均数为:.由已知得用样本估计总体可知,估计改进后该厂的所有产品评分的方差为:
,
,,
同理,,
式
.
(2)将这1500万元用于改进一条生产线,一年后因产品评分提高而增加的收益为:
(元,将这1500万元购买该款理财产品,一年后的收益为:(元,
,将这1500万元用于改进一条生产线一年后收益更大.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
