2020-2021学年八年级数学人教版下册18.1.1平行四边形的性质课后培优(Word版含解析)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册18.1.1平行四边形的性质课后培优(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 643.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 18:13:35 | ||
图片预览

文档简介
平行四边形的性质
一、单选题
1.在平行四边形ABCD中,∠A+∠C=200°,则∠A的度数为( )
A.130°
B.100°
C.80°
D.70°
2.若平行四边形中两个内角的度数比为1:2,则其中较大的内角为(
)
A.90°
B.120°
C.135°
D.150°
3.已知平面直角坐标系中有O、A、B、C
四个点,其中点O
(0,0),
A(3,0),
B(1,1),若四边形OABC是平行四边形,则点C
的坐标为
(
)
A.(4,-1)
B.(4,1)
C.(2,-1)
D.(-2,1)
4.如图,平行四边形ABCD的周长为36cm,ABC的周长为28cm,则对角线AC的长为( )
A.28cm
B.18cm
C.10cm
D.8cm
5.如图,平行四边形ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,若平行四边形ABCD的周长为18,则△ABE的周长为(
)
A.8
B.9
C.10
D.18
6.如图,点O是的对称中心,,E、F是边上的点,且,G、H是边上的点,且,若分别表示和的面积,则与之间的等量关系是(
)
A.
B.
C.
D.
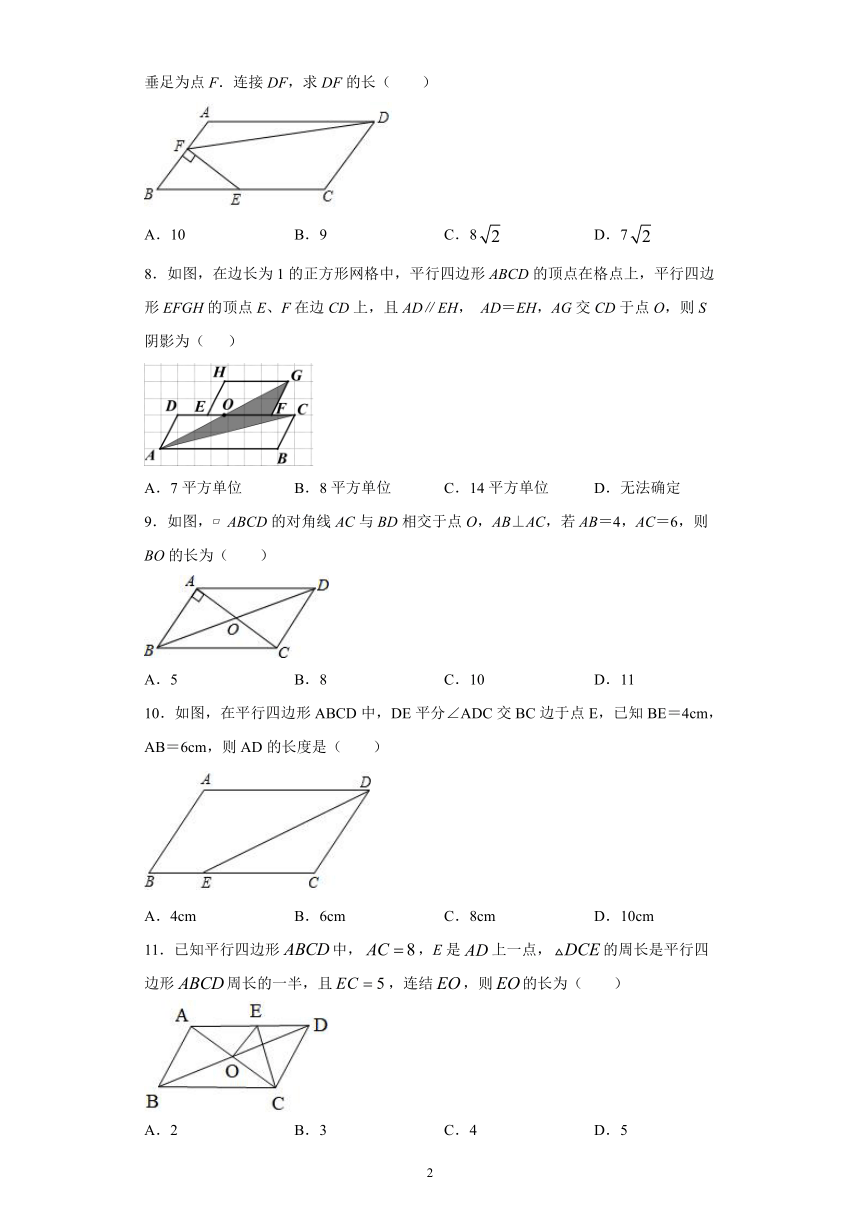
7.如图:在平行四边形ABCD中,AB=5,AD=10,BF=3,过BC的中点E作EF⊥AB,垂足为点F.连接DF,求DF的长( )
A.10
B.9
C.8
D.7
8.如图,在边长为1的正方形网格中,平行四边形ABCD的顶点在格点上,平行四边形EFGH的顶点E、F在边CD上,且AD∥EH,
AD=EH,AG交CD于点O,则S阴影为(
)
A.7平方单位
B.8平方单位
C.14平方单位
D.无法确定
9.如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BO的长为( )
A.5
B.8
C.10
D.11
10.如图,在平行四边形ABCD中,DE平分∠ADC交BC边于点E,已知BE=4cm,AB=6cm,则AD的长度是(
)
A.4cm
B.6cm
C.8cm
D.10cm
11.已知平行四边形中,,E是上一点,的周长是平行四边形周长的一半,且,连结,则的长为(
)
A.2
B.3
C.4
D.5
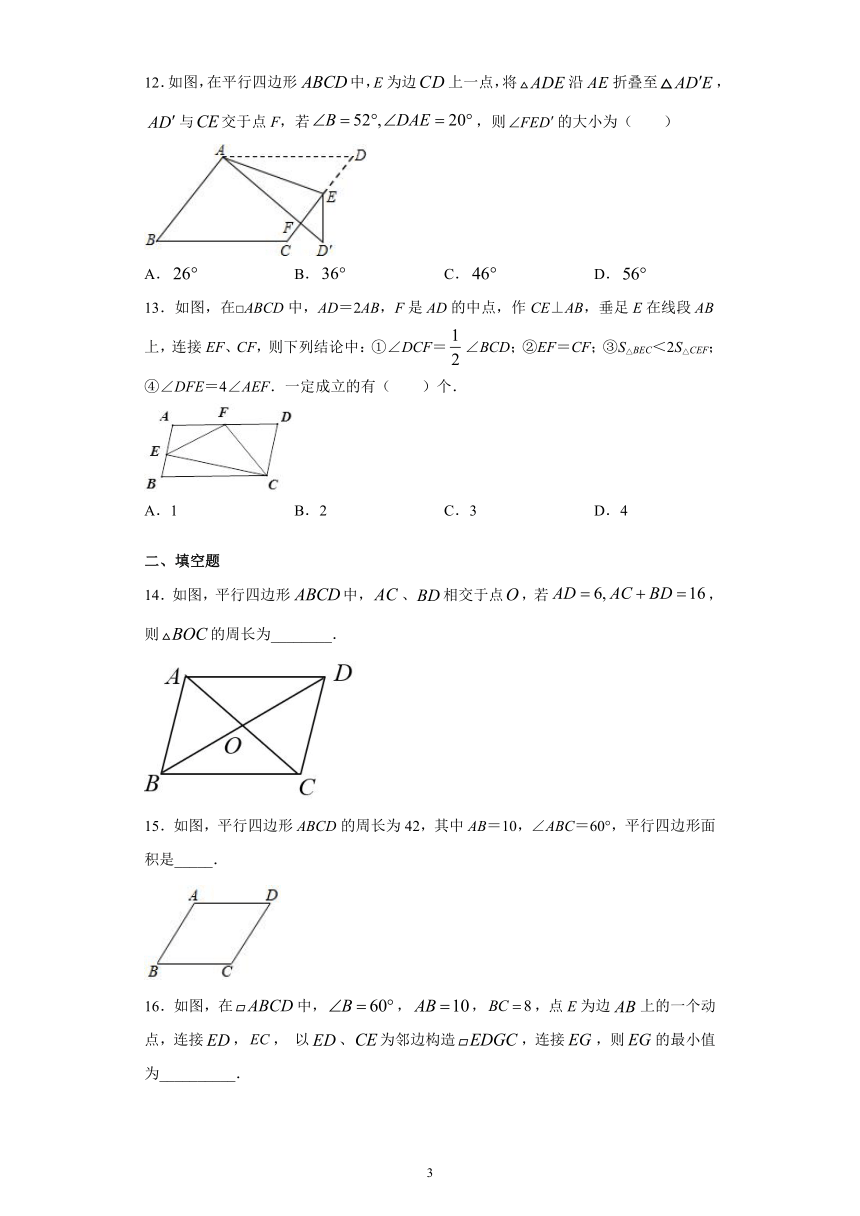
12.如图,在平行四边形中,E为边上一点,将沿折叠至,与交于点F,若,则的大小为(
)
A.
B.
C.
D.
13.如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中:①∠DCF=∠BCD;②EF=CF;③S△BEC<2S△CEF;④∠DFE=4∠AEF.一定成立的有( )个.
A.1
B.2
C.3
D.4
二、填空题
14.如图,平行四边形中,、相交于点,若,则的周长为________.
15.如图,平行四边形ABCD的周长为42,其中AB=10,∠ABC=60°,平行四边形面积是_____.
16.如图,在中,,,,点E为边上的一个动点,连接,,
以、为邻边构造,连接,则的最小值为__________.
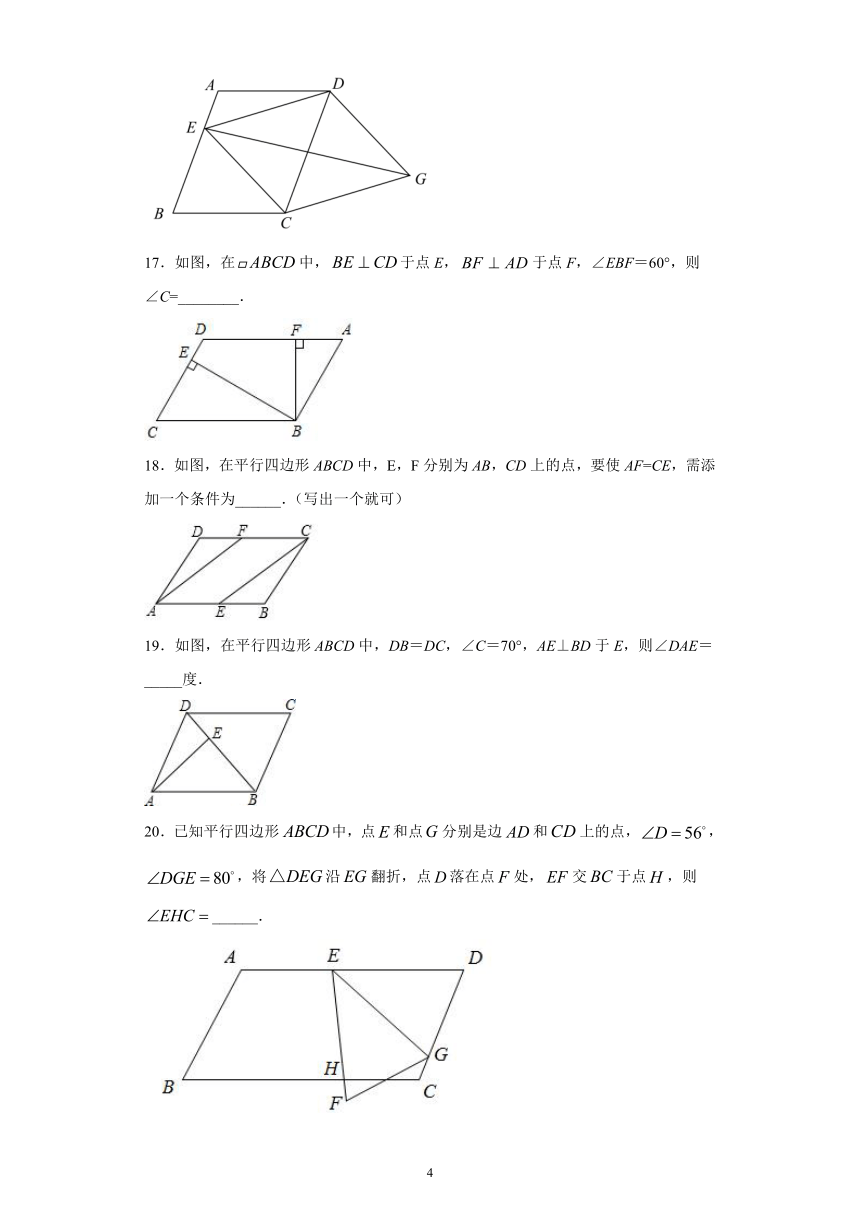
17.如图,在中,于点E,于点F,∠EBF=60°,则∠C=________.
18.如图,在平行四边形ABCD中,E,F分别为AB,CD上的点,要使AF=CE,需添加一个条件为______.(写出一个就可)
19.如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=_____度.
20.已知平行四边形中,点和点分别是边和上的点,,,将沿翻折,点落在点处,交于点,则______.
三、解答题
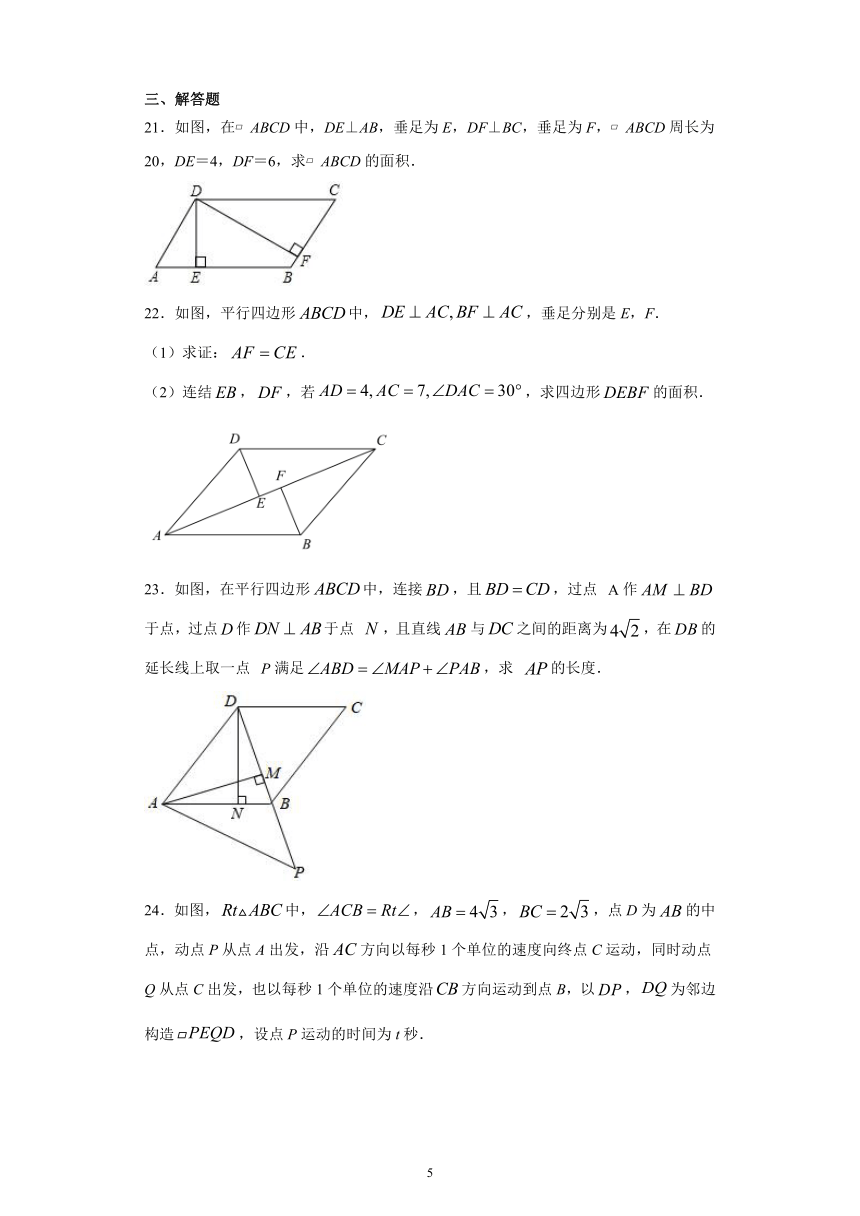
21.如图,在?ABCD中,DE⊥AB,垂足为E,DF⊥BC,垂足为F,?ABCD周长为20,DE=4,DF=6,求?ABCD的面积.
22.如图,平行四边形中,,垂足分别是E,F.
(1)求证:.
(2)连结,,若,求四边形的面积.
23.如图,在平行四边形中,连接,且,过点
作于点,过点作于点
,且直线与之间的距离为,在的延长线上取一点
满足,求
的长度.
24.如图,中,,,,点D为的中点,动点P从点A出发,沿方向以每秒1个单位的速度向终点C运动,同时动点Q从点C出发,也以每秒1个单位的速度沿方向运动到点B,以,为邻边构造,设点P运动的时间为t秒.
(1)当时,求的长;
(2)如图2,当点Q运动至点B时,连结,求证:.
(3)如图3,连结,当点E恰好落在的边上时,求所有满足要求的t值.
参考答案
1.B
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
又∵∠A+∠C=200°,
∴∠A=100°.
2.B
解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠B:∠C=1:2,
∴∠C=23×180°=120°,
3.D
解:如图,∵四边形OABC是平行四边形,点O
(0,0),
A(3,0),
B(1,1),
∴BC=AO=3,
故点C
的坐标为B(1-3,1),即(-2,1)
4.C
解:∵?ABCD的周长是36cm,
∴AB+AD=18m,
∵△ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=(AB+BC+AC)﹣(AB+AC)=28﹣18=10(cm).
5.B
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC,
∵平行四边形ABCD的周长是18cm,
∴AB+AD=9cm,
∵OE⊥BD,OB=OD,
∴BE是BD的垂直平分线,
∴BE=DE,
∴△ABE的周长为:AB+AE+BE=AB+AE+DE=AB+AD=9cm.
6.B
解:如图,连接OA,OB,OC.设平行四边形的面积为4s.
∵点O是平行四边形ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD=s,
∵EF=AB,3GH=BC,
∴S1=s,S2=s,
∴,
7.C
解:延长,,交于点,
四边形是平行四边形,
,,,
,.
,,
,.
是的中点,
,
在和中
,
,.
,
,
,
在中,,
则由勾股定理可得:,
,,
在中,,
则由勾股定理可得:
.
8.A
解:∵四边形ABCD是平行四边形,
∴四边形ABCD的面积=7×2=14,
∵四边形EFGH是平行四边形,
∴EH//GF,EH=GF,
∵AD//EH,
AD=EH,
∴AD//GF,EH=AD,
∴∠DAO=∠FGO,
∵∠DOA=∠FOG,
∴△DOA≌△FOG
∴,
∴,
9.A
解:∵四边形ABCD是平行四边形,
∴AO=CO=AC=3,
∵AB⊥AC,AB=4,
∴BO=,
10.D
解:已知平行四边形ABCD,DE平分∠ADC,
∴AD∥BC,CD=AB=6cm,∠EDC=∠ADE,AD=BC,
∴∠DEC=∠ADE,
∴∠DEC=∠CDE,
∴CE=CD=6cm,
∴BC=BE+CE=4+6=10cm,
∴AD=BC=10cm,
11.B
解:∵的周长是平行四边形周长的一半,即AD+CD=CD+DE+EC,
∴AE=EC=5,即为等腰三角形.
∵点O是平行四边形对角线交点,
∴点O为AC中点.
∴EO垂直平分AC.
∴AO=4.
在中,.
12.B
解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°-∠EAD′-∠D′=108°,
∴∠FED′=108°-72°=36°;
13.C
解:①∵F是AD的中点,
∴AF=FD,
∵在中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵
,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=
∠BCD,
故①正确;
②延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,即,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∴
∵,
∴CF=EF,
故②正确;
③∵EF=FM,
∴,
∴,
∵MC>BE,
∴
∴故③正确;
④设∠FEC=x,
∵CE⊥AB,,
∴,
∵F
是EM的中点,
∴FC=FE,
∴∠FCE=x,
∴,
∵
∴∠FCB=∠DFC
∵∠DCF=∠FCB;
∴∠DCF=∠DFC
∴
∴,
∴,
∵,
∴∠DFE=3∠AEF,故④错误.
综上所述正确的是:①②③.
14.14
解:∵四边形ABCD是平行四边形,
∴AD=BC=6,OA=OC,OB=OD,
∵AC+BD=16,
∴OB+OC=8,
∴△BOC的周长=BC+OB+OC=6+8=14.
15.55
解:如图,过点A作AE⊥BC于点E,
∵AB=10,∠ABC=60°,
∴∠BAE=90°-∠ABC=30°,
∴BE=AB=5,
∴AE==BE=5,
平行四边形ABCD的周长为42,
∴AB+BC=21,
∴BC=21﹣10=11,
∴平行四边形面积是BC?AE=11×5=55.
16.
解:∵四边形EDGC是平行四边形,
∴EF=FG,
∴当EF⊥CD时,EF最小,此时EG最小,
过点C作CH⊥AB于点H,则CH=EF,
∵∠B=60°,
∴∠BCH=30°,
∵BC=8,
∴BH=4,
∴CH==,
∴EF的最小值为,
∴EG的最小值为,
17.60°
解:∵BE⊥CD,BF⊥AD,
∴∠BED=∠BFD=90°,
在四边形BEDF中,∠D=360°?∠BED
?∠BFD
?∠EBF=360°?90°?90°?60°=120°,
在?ABCD中,∠C=180°?∠D=180°?120°=60°.
18.BE=DF
(答案非唯一)
解:添加条件BE=DF.
∵平行四边形ABCD,
∴BC=AD,∠B=∠D
在△EBC和△FDA中
∵BC=AD,∠B=∠D,BE=DF
∴△EBC≌△FDA(SAS)
∴AF=CE
19.20
解:∵DB=DC,∠C=70°,
∴∠DBC=∠C=70°,
∵四边形ABCD是平行四边形,AE⊥BD,
∴AD∥BC,
∠AED=90°,
∴∠ADB=∠DBC=∠C=70°,
∴∠DAE=90°﹣70°=20°.
20.
解:∵,
∴
∵沿翻折
∴
∴
∵四边形是平行四边形
∴
∴.
21.24
解:?ABCD周长为20,
,
设,则,根据平行四边形的面积公式可得:,
解之得,
即,
,,
平行四边形的面积等于.
22.(1)见解析;(2)
解:(1)∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠DCE=∠BAF,
∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°,
∴△CDE≌△ABF(AAS),
∴CE=AF;
(2)∵AD=4,∠DAC=30°,∠DEA=90°,
∴DE=2,
∴AE==,
同理:CF=,BF=DE=2,
∵AC=7,
∴EF=AC-AE-CF=7-,
∴四边形DEBF的面积==.
23.8.
解:在平行四边形中,,
∵
之间的距离为
(外角)
又
中,
24.(1);(2)见详解;(3)当点E恰好落在的边上时,t的值为或.
(1)解:由题意可得:,
∵,,,
∴,
∵点D为的中点,
∴,
过点P作PH⊥AB于点H,如图所示:
∵,
∴,
∴,
在Rt△AHP中,,
∴,
∴在Rt△PHD中,;
(2)证明:∵点Q运动至点B时,四边形是平行四边形,
∴PE∥BD,PE=BD,
∵点D为的中点,
∴,
∴PE∥AD,PE=AD,
∴四边形是平行四边形,
∴;
(3)由题意得:,
∵,,,
∴,
当点E恰好落在的边上时,则可分:
①当点E恰好落在的边上时,如图,
∵四边形是平行四边形,
∴PE=DQ,PD=QE,DQ∥AC,
∵∠ACB=90°,
∴,
∵点D为的中点,
∴,
∴,
∴,
∴,即;
②当点E恰好落在的边上时,如图,过点D、E分别作DN⊥BC,EM⊥AC,垂足分别为N、M,
∴,
∵四边形PEQD是平行四边形,
∴,
∴,
∵点D为的中点,
∴,
∴CN=BN,
∴,
由(1)得:,
∴,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴在Rt△CME中,,
∵,
∴,
解得:;
由题意可知点E恰好落在的边上是不存在的,
综上所述:当点E恰好落在的边上时,t的值为或.
一、单选题
1.在平行四边形ABCD中,∠A+∠C=200°,则∠A的度数为( )
A.130°
B.100°
C.80°
D.70°
2.若平行四边形中两个内角的度数比为1:2,则其中较大的内角为(
)
A.90°
B.120°
C.135°
D.150°
3.已知平面直角坐标系中有O、A、B、C
四个点,其中点O
(0,0),
A(3,0),
B(1,1),若四边形OABC是平行四边形,则点C
的坐标为
(
)
A.(4,-1)
B.(4,1)
C.(2,-1)
D.(-2,1)
4.如图,平行四边形ABCD的周长为36cm,ABC的周长为28cm,则对角线AC的长为( )
A.28cm
B.18cm
C.10cm
D.8cm
5.如图,平行四边形ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,若平行四边形ABCD的周长为18,则△ABE的周长为(
)
A.8
B.9
C.10
D.18
6.如图,点O是的对称中心,,E、F是边上的点,且,G、H是边上的点,且,若分别表示和的面积,则与之间的等量关系是(
)
A.
B.
C.
D.
7.如图:在平行四边形ABCD中,AB=5,AD=10,BF=3,过BC的中点E作EF⊥AB,垂足为点F.连接DF,求DF的长( )
A.10
B.9
C.8
D.7
8.如图,在边长为1的正方形网格中,平行四边形ABCD的顶点在格点上,平行四边形EFGH的顶点E、F在边CD上,且AD∥EH,
AD=EH,AG交CD于点O,则S阴影为(
)
A.7平方单位
B.8平方单位
C.14平方单位
D.无法确定
9.如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BO的长为( )
A.5
B.8
C.10
D.11
10.如图,在平行四边形ABCD中,DE平分∠ADC交BC边于点E,已知BE=4cm,AB=6cm,则AD的长度是(
)
A.4cm
B.6cm
C.8cm
D.10cm
11.已知平行四边形中,,E是上一点,的周长是平行四边形周长的一半,且,连结,则的长为(
)
A.2
B.3
C.4
D.5
12.如图,在平行四边形中,E为边上一点,将沿折叠至,与交于点F,若,则的大小为(
)
A.
B.
C.
D.
13.如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中:①∠DCF=∠BCD;②EF=CF;③S△BEC<2S△CEF;④∠DFE=4∠AEF.一定成立的有( )个.
A.1
B.2
C.3
D.4
二、填空题
14.如图,平行四边形中,、相交于点,若,则的周长为________.
15.如图,平行四边形ABCD的周长为42,其中AB=10,∠ABC=60°,平行四边形面积是_____.
16.如图,在中,,,,点E为边上的一个动点,连接,,
以、为邻边构造,连接,则的最小值为__________.
17.如图,在中,于点E,于点F,∠EBF=60°,则∠C=________.
18.如图,在平行四边形ABCD中,E,F分别为AB,CD上的点,要使AF=CE,需添加一个条件为______.(写出一个就可)
19.如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE=_____度.
20.已知平行四边形中,点和点分别是边和上的点,,,将沿翻折,点落在点处,交于点,则______.
三、解答题
21.如图,在?ABCD中,DE⊥AB,垂足为E,DF⊥BC,垂足为F,?ABCD周长为20,DE=4,DF=6,求?ABCD的面积.
22.如图,平行四边形中,,垂足分别是E,F.
(1)求证:.
(2)连结,,若,求四边形的面积.
23.如图,在平行四边形中,连接,且,过点
作于点,过点作于点
,且直线与之间的距离为,在的延长线上取一点
满足,求
的长度.
24.如图,中,,,,点D为的中点,动点P从点A出发,沿方向以每秒1个单位的速度向终点C运动,同时动点Q从点C出发,也以每秒1个单位的速度沿方向运动到点B,以,为邻边构造,设点P运动的时间为t秒.
(1)当时,求的长;
(2)如图2,当点Q运动至点B时,连结,求证:.
(3)如图3,连结,当点E恰好落在的边上时,求所有满足要求的t值.
参考答案
1.B
解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
又∵∠A+∠C=200°,
∴∠A=100°.
2.B
解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠B:∠C=1:2,
∴∠C=23×180°=120°,
3.D
解:如图,∵四边形OABC是平行四边形,点O
(0,0),
A(3,0),
B(1,1),
∴BC=AO=3,
故点C
的坐标为B(1-3,1),即(-2,1)
4.C
解:∵?ABCD的周长是36cm,
∴AB+AD=18m,
∵△ABC的周长是28cm,
∴AB+BC+AC=28cm,
∴AC=(AB+BC+AC)﹣(AB+AC)=28﹣18=10(cm).
5.B
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC,
∵平行四边形ABCD的周长是18cm,
∴AB+AD=9cm,
∵OE⊥BD,OB=OD,
∴BE是BD的垂直平分线,
∴BE=DE,
∴△ABE的周长为:AB+AE+BE=AB+AE+DE=AB+AD=9cm.
6.B
解:如图,连接OA,OB,OC.设平行四边形的面积为4s.
∵点O是平行四边形ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD=s,
∵EF=AB,3GH=BC,
∴S1=s,S2=s,
∴,
7.C
解:延长,,交于点,
四边形是平行四边形,
,,,
,.
,,
,.
是的中点,
,
在和中
,
,.
,
,
,
在中,,
则由勾股定理可得:,
,,
在中,,
则由勾股定理可得:
.
8.A
解:∵四边形ABCD是平行四边形,
∴四边形ABCD的面积=7×2=14,
∵四边形EFGH是平行四边形,
∴EH//GF,EH=GF,
∵AD//EH,
AD=EH,
∴AD//GF,EH=AD,
∴∠DAO=∠FGO,
∵∠DOA=∠FOG,
∴△DOA≌△FOG
∴,
∴,
9.A
解:∵四边形ABCD是平行四边形,
∴AO=CO=AC=3,
∵AB⊥AC,AB=4,
∴BO=,
10.D
解:已知平行四边形ABCD,DE平分∠ADC,
∴AD∥BC,CD=AB=6cm,∠EDC=∠ADE,AD=BC,
∴∠DEC=∠ADE,
∴∠DEC=∠CDE,
∴CE=CD=6cm,
∴BC=BE+CE=4+6=10cm,
∴AD=BC=10cm,
11.B
解:∵的周长是平行四边形周长的一半,即AD+CD=CD+DE+EC,
∴AE=EC=5,即为等腰三角形.
∵点O是平行四边形对角线交点,
∴点O为AC中点.
∴EO垂直平分AC.
∴AO=4.
在中,.
12.B
解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°-∠EAD′-∠D′=108°,
∴∠FED′=108°-72°=36°;
13.C
解:①∵F是AD的中点,
∴AF=FD,
∵在中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵
,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=
∠BCD,
故①正确;
②延长EF,交CD延长线于M,
∵四边形ABCD是平行四边形,
∴,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,即,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∴
∵,
∴CF=EF,
故②正确;
③∵EF=FM,
∴,
∴,
∵MC>BE,
∴
∴故③正确;
④设∠FEC=x,
∵CE⊥AB,,
∴,
∵F
是EM的中点,
∴FC=FE,
∴∠FCE=x,
∴,
∵
∴∠FCB=∠DFC
∵∠DCF=∠FCB;
∴∠DCF=∠DFC
∴
∴,
∴,
∵,
∴∠DFE=3∠AEF,故④错误.
综上所述正确的是:①②③.
14.14
解:∵四边形ABCD是平行四边形,
∴AD=BC=6,OA=OC,OB=OD,
∵AC+BD=16,
∴OB+OC=8,
∴△BOC的周长=BC+OB+OC=6+8=14.
15.55
解:如图,过点A作AE⊥BC于点E,
∵AB=10,∠ABC=60°,
∴∠BAE=90°-∠ABC=30°,
∴BE=AB=5,
∴AE==BE=5,
平行四边形ABCD的周长为42,
∴AB+BC=21,
∴BC=21﹣10=11,
∴平行四边形面积是BC?AE=11×5=55.
16.
解:∵四边形EDGC是平行四边形,
∴EF=FG,
∴当EF⊥CD时,EF最小,此时EG最小,
过点C作CH⊥AB于点H,则CH=EF,
∵∠B=60°,
∴∠BCH=30°,
∵BC=8,
∴BH=4,
∴CH==,
∴EF的最小值为,
∴EG的最小值为,
17.60°
解:∵BE⊥CD,BF⊥AD,
∴∠BED=∠BFD=90°,
在四边形BEDF中,∠D=360°?∠BED
?∠BFD
?∠EBF=360°?90°?90°?60°=120°,
在?ABCD中,∠C=180°?∠D=180°?120°=60°.
18.BE=DF
(答案非唯一)
解:添加条件BE=DF.
∵平行四边形ABCD,
∴BC=AD,∠B=∠D
在△EBC和△FDA中
∵BC=AD,∠B=∠D,BE=DF
∴△EBC≌△FDA(SAS)
∴AF=CE
19.20
解:∵DB=DC,∠C=70°,
∴∠DBC=∠C=70°,
∵四边形ABCD是平行四边形,AE⊥BD,
∴AD∥BC,
∠AED=90°,
∴∠ADB=∠DBC=∠C=70°,
∴∠DAE=90°﹣70°=20°.
20.
解:∵,
∴
∵沿翻折
∴
∴
∵四边形是平行四边形
∴
∴.
21.24
解:?ABCD周长为20,
,
设,则,根据平行四边形的面积公式可得:,
解之得,
即,
,,
平行四边形的面积等于.
22.(1)见解析;(2)
解:(1)∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠DCE=∠BAF,
∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°,
∴△CDE≌△ABF(AAS),
∴CE=AF;
(2)∵AD=4,∠DAC=30°,∠DEA=90°,
∴DE=2,
∴AE==,
同理:CF=,BF=DE=2,
∵AC=7,
∴EF=AC-AE-CF=7-,
∴四边形DEBF的面积==.
23.8.
解:在平行四边形中,,
∵
之间的距离为
(外角)
又
中,
24.(1);(2)见详解;(3)当点E恰好落在的边上时,t的值为或.
(1)解:由题意可得:,
∵,,,
∴,
∵点D为的中点,
∴,
过点P作PH⊥AB于点H,如图所示:
∵,
∴,
∴,
在Rt△AHP中,,
∴,
∴在Rt△PHD中,;
(2)证明:∵点Q运动至点B时,四边形是平行四边形,
∴PE∥BD,PE=BD,
∵点D为的中点,
∴,
∴PE∥AD,PE=AD,
∴四边形是平行四边形,
∴;
(3)由题意得:,
∵,,,
∴,
当点E恰好落在的边上时,则可分:
①当点E恰好落在的边上时,如图,
∵四边形是平行四边形,
∴PE=DQ,PD=QE,DQ∥AC,
∵∠ACB=90°,
∴,
∵点D为的中点,
∴,
∴,
∴,
∴,即;
②当点E恰好落在的边上时,如图,过点D、E分别作DN⊥BC,EM⊥AC,垂足分别为N、M,
∴,
∵四边形PEQD是平行四边形,
∴,
∴,
∵点D为的中点,
∴,
∴CN=BN,
∴,
由(1)得:,
∴,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴在Rt△CME中,,
∵,
∴,
解得:;
由题意可知点E恰好落在的边上是不存在的,
综上所述:当点E恰好落在的边上时,t的值为或.
