2020-2021学年人教版八年级数学下册第18章平行四边形期末练习(Word版含解析)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册第18章平行四边形期末练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 11:08:10 | ||
图片预览

文档简介
平行四边形期末练习
一、单选题(每小题3分,共36分)
1.如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.OA=OC,OB=OD
D.AB∥DC,AD=BC
2.如图,两把完全一样的直尺叠放在起,重合的部分构成一个四边形,给出以下四个论断:①这个四边形可能是正方形;②这个四边形一定是菱形;③这个四边形不可能是矩形;④这个四边形一定是轴对称图形,其中正确的论断是(
)
A.①②
B.③④
C.①②④
D.①②③④
3.如图,四边形和均为正方形,点在对角线上,点在边上,连结和.若知道正方形和的面积,则一定能求出(
)
A.四边形的周长
B.四边形的周长
C.四边形的周长
D.四边形的周长
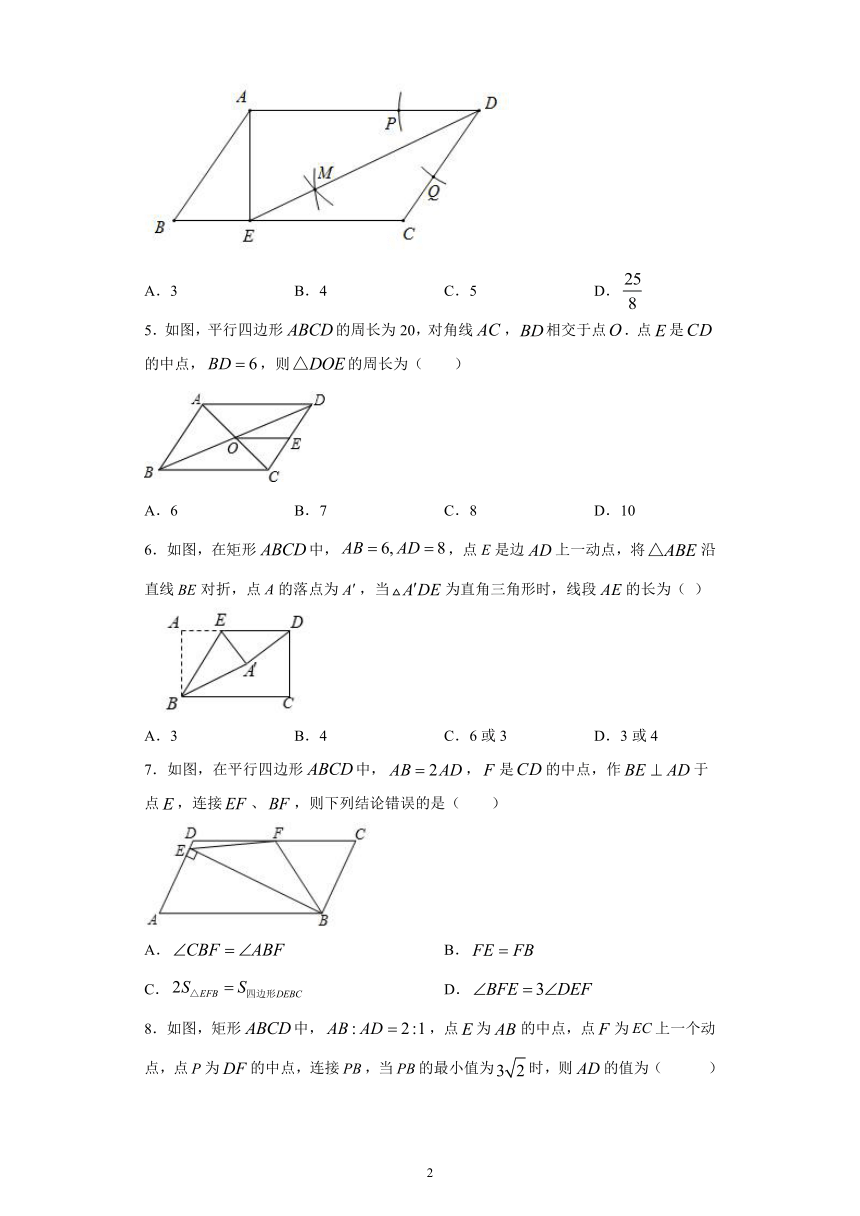
4.如图,在平行四边形ABCD中,AB=5,BC=8,以点D为圆心,任意长为半径画弧,交AD于点P,交CD于点Q,分别以P、Q为圆心,大于PQ为半径画弧交于点M,连接DM并延长,交BC于点E,连接AE,恰好有AE⊥BC,则AE的长为(
)
A.3
B.4
C.5
D.
5.如图,平行四边形的周长为20,对角线,相交于点.点是的中点,,则的周长为(
)
A.6
B.7
C.8
D.10
6.如图,在矩形中,,点E是边上一动点,将沿直线对折,点A的落点为,当为直角三角形时,线段的长为(
)
A.3
B.4
C.6或3
D.3或4
7.如图,在平行四边形中,,是的中点,作于点,连接、,则下列结论错误的是(
)
A.
B.
C.
D.
8.如图,矩形中,,点为的中点,点为上一个动点,点为的中点,连接,当的最小值为时,则的值为(
)
A.2
B.3
C.4
D.6
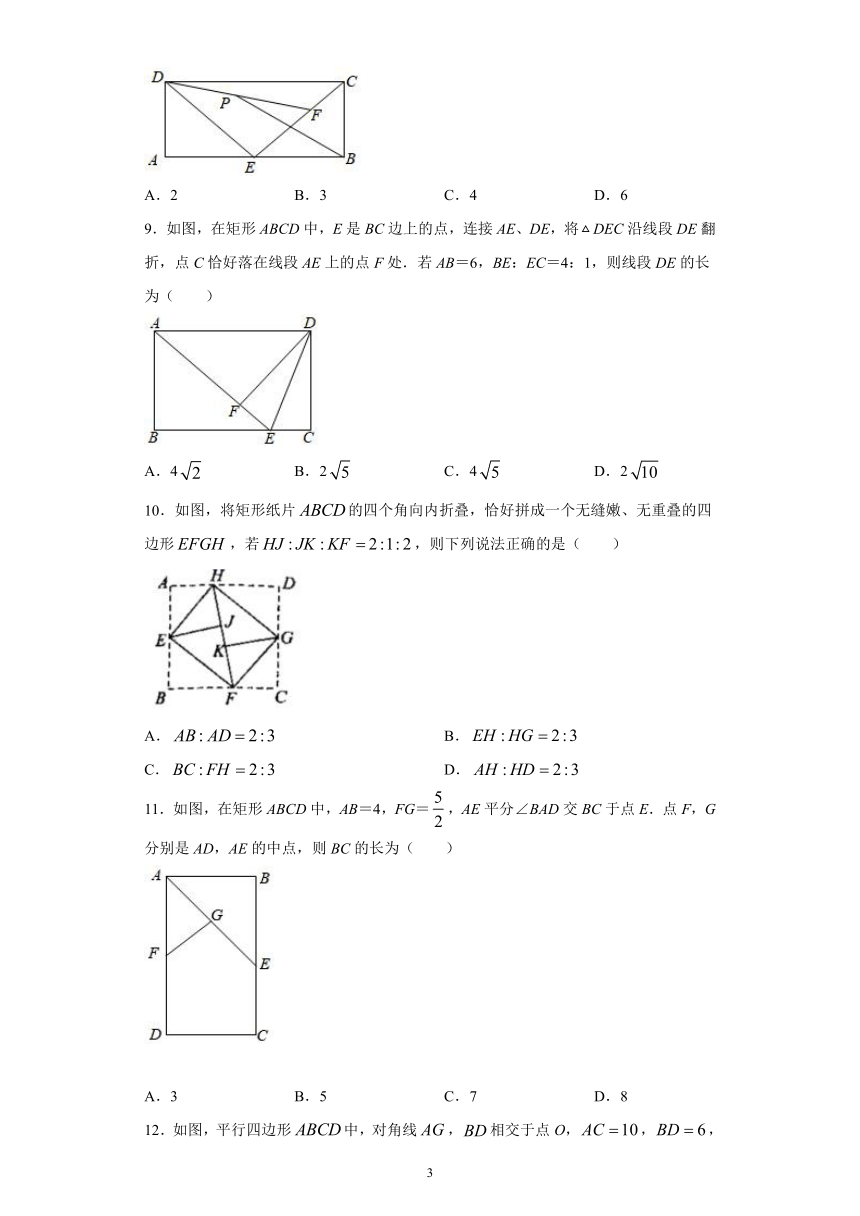
9.如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE:EC=4:1,则线段DE的长为(
)
A.4
B.2
C.4
D.2
10.如图,将矩形纸片的四个角向内折叠,恰好拼成一个无缝嫩、无重叠的四边形,若,则下列说法正确的是(
)
A.
B.
C.
D.
11.如图,在矩形ABCD中,AB=4,FG=,AE平分∠BAD交BC于点E.点F,G分别是AD,AE的中点,则BC的长为( )
A.3
B.5
C.7
D.8
12.如图,平行四边形中,对角线,相交于点O,,,.在边上取一点E,使,则的面积为(
)
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
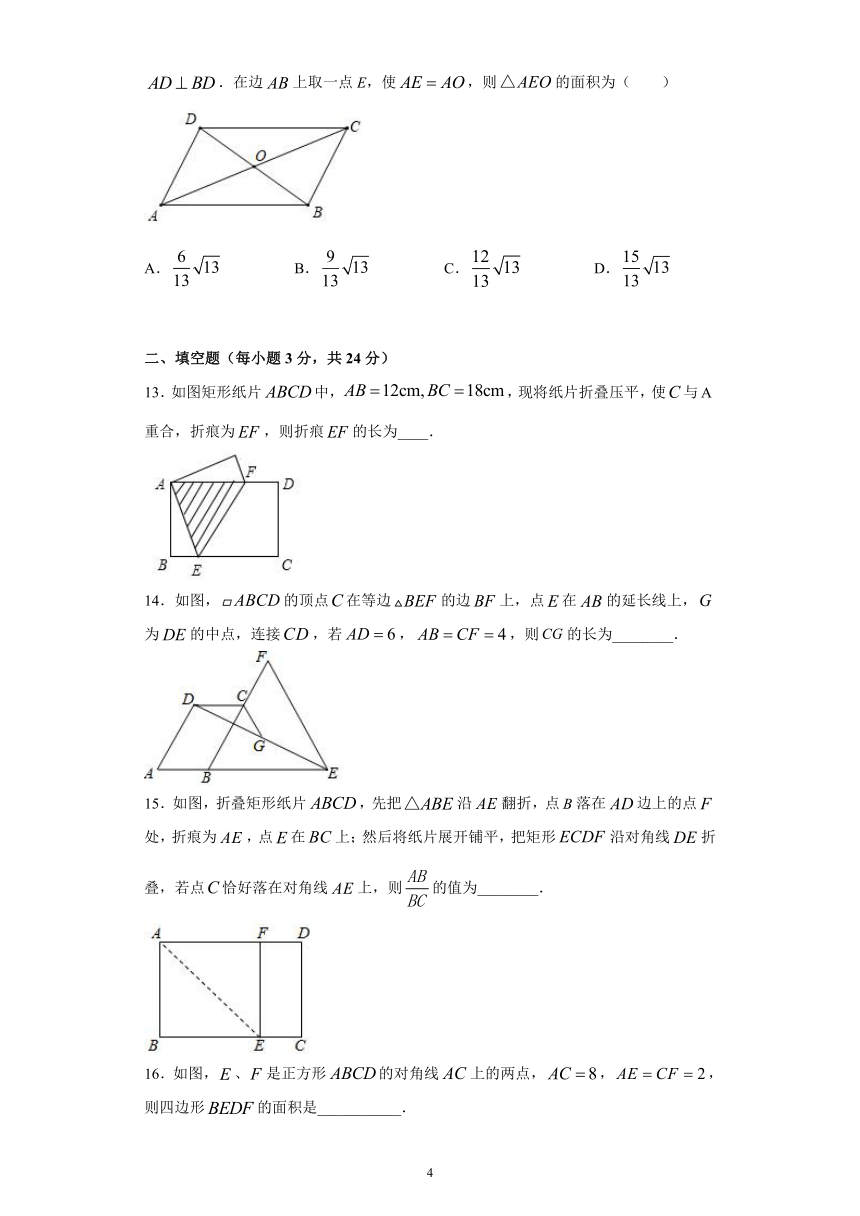
13.如图矩形纸片中,,现将纸片折叠压平,使与重合,折痕为,则折痕的长为____.
14.如图,的顶点在等边的边上,点在的延长线上,为的中点,连接,若,,则的长为________.
15.如图,折叠矩形纸片,先把沿翻折,点落在边上的点处,折痕为,点在上;然后将纸片展开铺平,把矩形沿对角线折叠,若点恰好落在对角线上,则的值为________.
16.如图,、是正方形的对角线上的两点,,,则四边形的面积是___________.
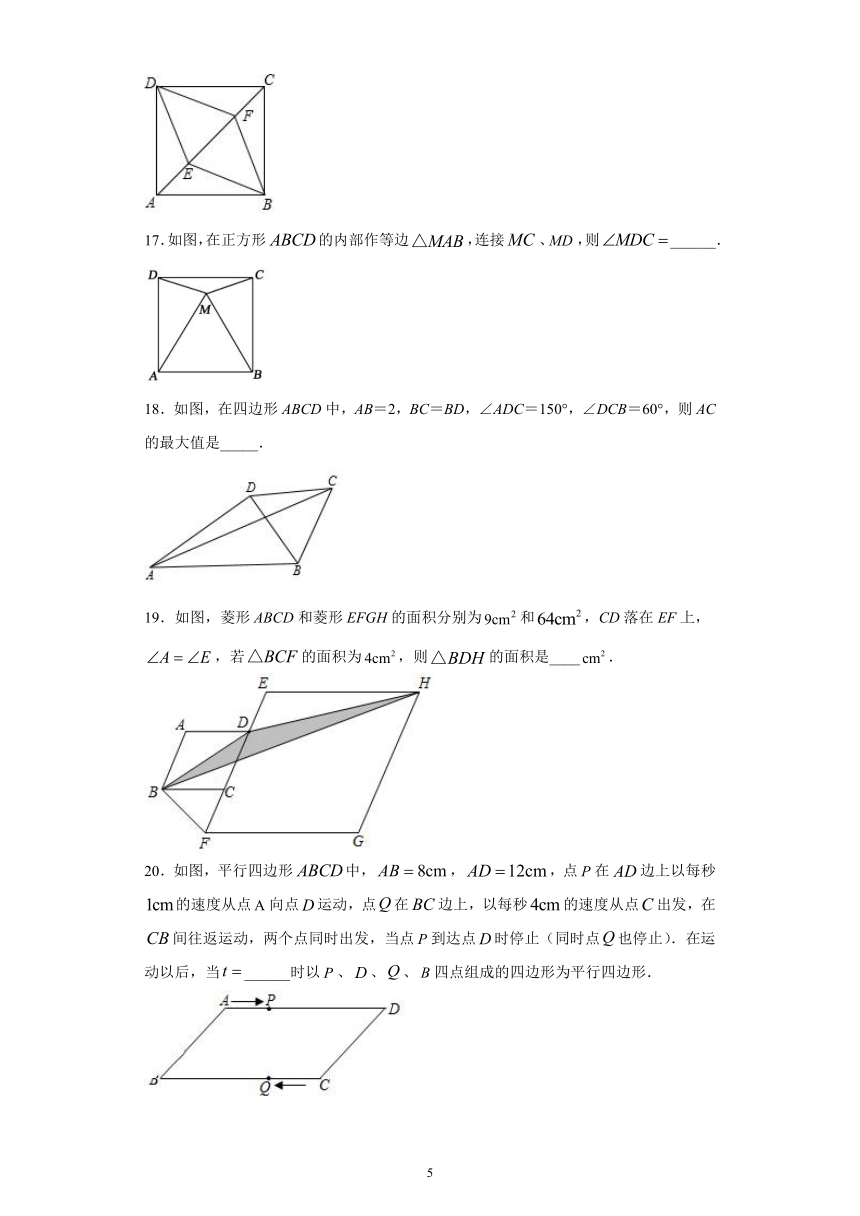
17.如图,在正方形的内部作等边,连接、,则______.
18.如图,在四边形ABCD中,AB=2,BC=BD,∠ADC=150°,∠DCB=60°,则AC的最大值是_____.
19.如图,菱形ABCD和菱形EFGH的面积分别为和,CD落在EF上,,若的面积为,则的面积是____.
20.如图,平行四边形中,,,点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点出发,在间往返运动,两个点同时出发,当点到达点时停止(同时点也停止).在运动以后,当______时以、、、四点组成的四边形为平行四边形.
三、解答题(本大题共60分)
21.(8分)如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F.
求证:AE=DF.
22.(8分)已知:平行四边形ABCD,过点A、C分别作AD、BC的垂线,交BD于E、F两点,连接AF、CE.
(1)如图1,求证:四边形AECF是平行四边形;
(2)如图2,当点F为DE中点时,请直接写出图2中与四边形AECF面积相等的所有三角形.
23.(8分)如图,在菱形ABCD中,AC,BD相交于点O,过B,C两点分别作AC,BD的平行线,相交于点E.
(1)求证:四边形BOCE是矩形;
(2)连接EO交BC于点F,连接AF,若∠ABC=60°,AB=2,求AF的长.
24.(8分)如图1,已知四边形是平行四边形,并且.
(1)求证:四边形为矩形;
(2)如图2,点E是边的中点,F为边上一点,.若,,求的长.
25(8分)如图,在四边形中,,对角线的垂直平分线与边分别相交于点M、N.
(1)求证:四边形是菱形;
(2)若,菱形的面积为120,求菱形的周长.
26.(10分)已知,点E在正方形ABCD的AB边上(不与点A,B重合),BD是对角线,延长AB到点F,使BF=AE,过点E作BD的垂线,垂足为M,连接AM,CF.
(1)根据题意补全图形,并证明MB=ME;
(2)①用等式表示线段AM与CF的数量关系,并证明;
②直接用等式表示线段AM,BM,DM之间的数量关系.
27.(10分)如图,在正方形中,是上一点,是延长线上一点,且.
(1)求证:;
(2)点在上,连结,,若,求此时的大小.
参考答案
1.D
解:∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,
故选项A不符合题意;
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形,
故选项B不符合题意;
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
故选项C不符合题意;
∵AB∥DC,AD=BC,
∴四边形ABCD不一定是平行四边形,也可能是等腰梯形,故选项D符合题意,
2.C
解:过点作于,于.
两张长方形直尺的宽度相等,
,
又平行四边形的面积,
,
平行四边形为菱形.故②正确
当时,这个四边形是正方形,故①正确,③不正确
这个四边形一定是轴对称图形,故④正确
3.B
解:四边形和均为正方形,
,
.
四边形的周长
.
因为知道正方形和的面积,
所以它们的边长和对角线均可确定,
即与确定,一定能求出四边形的周长,其他选项不符合;
4.B
根据作图可知DE为的角平分线,即,
∵四边形ABCD为平行四边形,
∴,
∴,
∴,
∴,
∴,
∴在中,.
5.C
解:的周长为20,
,则.
四边形是平行四边形,对角线,相交于点,,
.
点是的中点,
是的中位线,,
,
的周长,
即的周长为8.
6.C
解:∵四边形ABCD是矩形
∴∠A=∠C=90°,AB=6,AD=8
∴
当为直角三角形时,有两种情况:
①当点在矩形内部时,如图1所示,
由折叠的性质得,,
设,则,
∴
在Rt中,
∴
解得,x=3
∴AE=3;
②当点落在边BC上时,如图2所示,
此时四边形是正方形,
∴AE=AB=6
7.D
解:如图延长交的延长线于,取的中点,连接.
∵,
∴,
∵是的中点,
∴,
∴,
∴,
∵,
∴,
∴,故A正确,
∵,
∴,
∵,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,故B正确,
∵,
∴
,故C正确,
∵,,,
∴,
∵,
∴四边形是平行四边形,
∵,
∴四边形是菱形,
∴,
∵,,,
∴,
∴,
∴,故D错误,
8.B
解:如图,
当点F与点C重合时,点P在P1处,CP1=DP1,
当点F与点E重合时,点P在P2处,EP2=DP2,
∴P1P2∥CE且P1P2=CE.
且当点F在EC上除点C、E的位置处时,有DP=FP.
由中位线定理可知:P1P∥CE且P1P=CF,
∴点P的运动轨迹是线段P1P2,
.∴当BP⊥P1P2时,PB取得最小值.
∵矩形ABCD中,AB:AD=2:1,设AB=2t,则AD=t,
∵E为AB的中点,
∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=t,
∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.
∴∠DP2P1=90°.
∴∠DP1P2=45°.
∴∠P2P1B=90°,即BP1⊥P1P2,
∴BP的最小值为BP1的长.
在等腰直角△BCP1中,CP1=BC=t,
∴BP1=t=,
∴t=3.
9.D
解:由矩形ABCD,得∠B=∠C=90°,CD=AB,AD=BC,AD∥BC.
由△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处,得△DFE≌△DCE,
∴DF=DC,∠DFE=∠C=90°,
∴DF=AB,∠AFD=90°,
∴∠AFD=∠B,
由AD∥BC得∠DAF=∠AEB,
在△ABE与△DFA中,
,
∴△ABE≌△DFA(AAS).
∵BE:CE=4:1,
∴设CE=x,BE=4x,则AD=BC=5x,
由△ABE≌△DFA,得AF=BE=4x,
在Rt△ADF中,由勾股定理可得DF=3x,
又∵DF=CD=AB=6,
∴x=2,
在Rt△DCE中,DE===2.
10.D
解:∵HJ:JK:KF=2:1:2,
∴设HJ=2x,JK=x,KF=2x,
由折叠的性质得:AH=HJ=2x,
DH
=HK=3x,AE=EJ=
BE,
∴FH=5x,
∴AH:HD=2:3,
故D说法正确;
11.C
解:连接DE,
∵FG=且F、G分别为AD、AE中点,
∴DE=2FG=5,
∵四边形ABCD为矩形,
∴CD=AB=4,
在△CDE中,CE==3,
∵AE平分∠BAD,四边形ABCD为矩形,
∴∠BAD=∠ABE=90°,
∴∠BAE=∠BAD=45°,
在△ABE中,∠AEB=90°﹣∠AEB=45°,
∴∠BAE=∠AEB=45°,
△ABE为等腰直角三角形,
∴BE=AB=4,
又∵CE=3,
∴BC=BE+CE=4+3=7.
12.D
解:如图所示,过作于,过作于,
平行四边形中,,,
,,
又,
中,,
中,,
,
,
,,
,
又,
,
13.
如图所示:过点F作FN⊥BC交BC于点N,
设BE=xcm,则AE=BC=18-x,
在Rt△ABE中,,即
,
解得x=5,
∴AE=,
在矩形纸片中,则AE//MF,AD//BC,AB=AM,
∴∠AEB=∠FAE=∠AFM,
在△ABE和△AMF中
,
∴△ABE≌△AMF(AAS),
∴AF=AE=13cm,
∴DF=AD-AF=5,
∴EN=BC-BE-CN=BC-BE-DF=8,
在Rt△ENF中,EF=
.
14.3
解:如图,延长交于点,
四边形是平行四边形,
,,,
,,
,,
,
是等边三角形,为的中点,
,,
,
,
在和中,
,
,
,,
,,
,,
,,
是等边三角形,
,
,
15.
解:连接DE,如图,
由折叠可得,EF=BE,∠AFE=90°,∠AED=∠CED,
∵矩形ABCD,
∴BC=AD,∠BAF=∠B=90°,AD∥BC,
∴∠BAF=∠B=∠AFE=90°,∠ADE=∠DEC,
∴四边形ABEF为正方形,∠ADE=∠AED,
∴AB=BE=EF=AF,AD=AE,
设AB=a,则BC=AD=AE=a,
∴,
16.16
解:如图,连接BD交AC于点O,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC,
∵AE=CF=2,
∴OA-AE=OC-CF,即OE=OF,
∴四边形BEDF为平行四边形,且BD⊥EF,
∴四边形BEDF为菱形,
∴DE=DF=BE=BF,
∵AC=BD=8,OE=OF=,
∴EF=4,
∴四边形BEDF的面积为EF·BD==16,
17.15°
解:∵是等边三角形,
∴AM=AB=BM,∠MAB=60°,
∵四边形ABCD为正方形,
∴AD=AB,∠ADC=∠DAB=90°,
∴AM=AD,∠DAM=90°-∠MAB=90°-60°=30°,
∴∠ADM=∠AMD=,
∴∠MDC=∠ADC-∠ADM=90°-75°=15°.
18.1+
取AB的中点F,连接DF,
∠DCB=60°,BC=BD,
∠ADC=150°,AB=2,
以为边作等边,如图,连接,
则
为中点,
,
当且仅当过时,最长
此时.
19.8.5
解:连接FH,在菱形和菱形中,,
,
,
,
和同底等高,
菱形的面积为,,
,
,
20.4.8s或8s或9.6s
解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C-B,方程为12-4t=12-t,
此时方程t=0,此时不符合题意;
②点Q的运动路线是C-B-C,方程为4t-12=12-t,
解得:t=4.8;
③点Q的运动路线是C-B-C-B,方程为12-(4t-24)=12-t,
解得:t=8;
④点Q的运动路线是C-B-C-B-C,方程为4t-36=12-t,
解得:t=9.6;
综上所述,t=4.8s或8s或9.6s时,以P、D、Q、B四点组成的四边形为平行四边形,
21.见解析
证明:∵四边形ABCD是矩形,对角线AC,BD相交于点O,
∴OA=OC=OB=OD,
∵AE⊥BD,DF⊥AC,
∴∠AEO=∠DFO=90°,
在△AOE和△DOF中,
,
∴△AOE≌△DOF(AAS),
∴AE=DF.
22.(1)见解析;(2)△ABE,△ADE,△BCF,△DCE
证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,ADBC,
∴∠ADE=∠CBD,
∵AE⊥AD,CF⊥BC,
∴∠EAD=∠BCF=90°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
∴CF=AE,DE=BF,∠AEF=∠CFE,
∴AECF,
∴四边形AECF是平行四边形;
(2)∵点F为DE中点,
∴DF=EF,
∵BF=DE,
∴BE=DF=EF,
∴与四边形AECF面积相等有△ABF,△ADE,△BCF,△DCE.
23.(1)见解析;(2)
解:(1)∵BE∥AC,EC∥BD,
∴四边形BOCE是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠BOC=90°.
∴四边形BOCE是矩形.
(2)∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形.
∵四边形BOCE是矩形,
∴BF=BC=AB=1.
∴∠AFB=90°.
∴AF=.
24.(1)见解析;(2)
解:(1)∵四边形是平行四边形,
∴.
∵,
∴.
∴四边形是矩形.
(2)延长交于点G.
∵四边形是矩形,
∴,.
∴.
∵E是边的中点即,
∴.
∴.
∴.
∵,
∴.
∵,
∴.
∴.
设,由勾股定理得,
即:.解得.
25.(1)见解析;(2)52
解:(1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,
,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴四边形BNDM是菱形;
(2)∵BD=24,菱形BNDM的面积为120,
∴MN=120×2÷24=10,
∴BM=BN=DM=DN,OB=BD=12,OM=MN=5,
在Rt△BOM中,由勾股定理得:BM==13,
∴菱形BNDM的周长=4BM=4×13=52.
26.(1)见解析;(2)①,证明见解析;②
解:(1)如图所示,
四边形是正方形,是对角线,
,
,
是等腰直角三角形,
;
(2)①如图所示,连接、,
是等腰直角三角形,
,,
,
又,
,
,
,
,
,
,,
,
是等腰直角三角形,
,
即;
②,理由如下:
如图,连接,
,
,
又且,
,,
四边形是平行四边形,
,
,,
,
又,,
,
则.
27.(1)见解析;(2)45°
(1)证明:在正方形中,
∵,,,
∴.
∴.
(2)解:∵,
∴.
∵,,
∴.
∴,
∵,
又∵,
∴.
一、单选题(每小题3分,共36分)
1.如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是( )
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.OA=OC,OB=OD
D.AB∥DC,AD=BC
2.如图,两把完全一样的直尺叠放在起,重合的部分构成一个四边形,给出以下四个论断:①这个四边形可能是正方形;②这个四边形一定是菱形;③这个四边形不可能是矩形;④这个四边形一定是轴对称图形,其中正确的论断是(
)
A.①②
B.③④
C.①②④
D.①②③④
3.如图,四边形和均为正方形,点在对角线上,点在边上,连结和.若知道正方形和的面积,则一定能求出(
)
A.四边形的周长
B.四边形的周长
C.四边形的周长
D.四边形的周长
4.如图,在平行四边形ABCD中,AB=5,BC=8,以点D为圆心,任意长为半径画弧,交AD于点P,交CD于点Q,分别以P、Q为圆心,大于PQ为半径画弧交于点M,连接DM并延长,交BC于点E,连接AE,恰好有AE⊥BC,则AE的长为(
)
A.3
B.4
C.5
D.
5.如图,平行四边形的周长为20,对角线,相交于点.点是的中点,,则的周长为(
)
A.6
B.7
C.8
D.10
6.如图,在矩形中,,点E是边上一动点,将沿直线对折,点A的落点为,当为直角三角形时,线段的长为(
)
A.3
B.4
C.6或3
D.3或4
7.如图,在平行四边形中,,是的中点,作于点,连接、,则下列结论错误的是(
)
A.
B.
C.
D.
8.如图,矩形中,,点为的中点,点为上一个动点,点为的中点,连接,当的最小值为时,则的值为(
)
A.2
B.3
C.4
D.6
9.如图,在矩形ABCD中,E是BC边上的点,连接AE、DE,将DEC沿线段DE翻折,点C恰好落在线段AE上的点F处.若AB=6,BE:EC=4:1,则线段DE的长为(
)
A.4
B.2
C.4
D.2
10.如图,将矩形纸片的四个角向内折叠,恰好拼成一个无缝嫩、无重叠的四边形,若,则下列说法正确的是(
)
A.
B.
C.
D.
11.如图,在矩形ABCD中,AB=4,FG=,AE平分∠BAD交BC于点E.点F,G分别是AD,AE的中点,则BC的长为( )
A.3
B.5
C.7
D.8
12.如图,平行四边形中,对角线,相交于点O,,,.在边上取一点E,使,则的面积为(
)
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
13.如图矩形纸片中,,现将纸片折叠压平,使与重合,折痕为,则折痕的长为____.
14.如图,的顶点在等边的边上,点在的延长线上,为的中点,连接,若,,则的长为________.
15.如图,折叠矩形纸片,先把沿翻折,点落在边上的点处,折痕为,点在上;然后将纸片展开铺平,把矩形沿对角线折叠,若点恰好落在对角线上,则的值为________.
16.如图,、是正方形的对角线上的两点,,,则四边形的面积是___________.
17.如图,在正方形的内部作等边,连接、,则______.
18.如图,在四边形ABCD中,AB=2,BC=BD,∠ADC=150°,∠DCB=60°,则AC的最大值是_____.
19.如图,菱形ABCD和菱形EFGH的面积分别为和,CD落在EF上,,若的面积为,则的面积是____.
20.如图,平行四边形中,,,点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点出发,在间往返运动,两个点同时出发,当点到达点时停止(同时点也停止).在运动以后,当______时以、、、四点组成的四边形为平行四边形.
三、解答题(本大题共60分)
21.(8分)如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F.
求证:AE=DF.
22.(8分)已知:平行四边形ABCD,过点A、C分别作AD、BC的垂线,交BD于E、F两点,连接AF、CE.
(1)如图1,求证:四边形AECF是平行四边形;
(2)如图2,当点F为DE中点时,请直接写出图2中与四边形AECF面积相等的所有三角形.
23.(8分)如图,在菱形ABCD中,AC,BD相交于点O,过B,C两点分别作AC,BD的平行线,相交于点E.
(1)求证:四边形BOCE是矩形;
(2)连接EO交BC于点F,连接AF,若∠ABC=60°,AB=2,求AF的长.
24.(8分)如图1,已知四边形是平行四边形,并且.
(1)求证:四边形为矩形;
(2)如图2,点E是边的中点,F为边上一点,.若,,求的长.
25(8分)如图,在四边形中,,对角线的垂直平分线与边分别相交于点M、N.
(1)求证:四边形是菱形;
(2)若,菱形的面积为120,求菱形的周长.
26.(10分)已知,点E在正方形ABCD的AB边上(不与点A,B重合),BD是对角线,延长AB到点F,使BF=AE,过点E作BD的垂线,垂足为M,连接AM,CF.
(1)根据题意补全图形,并证明MB=ME;
(2)①用等式表示线段AM与CF的数量关系,并证明;
②直接用等式表示线段AM,BM,DM之间的数量关系.
27.(10分)如图,在正方形中,是上一点,是延长线上一点,且.
(1)求证:;
(2)点在上,连结,,若,求此时的大小.
参考答案
1.D
解:∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,
故选项A不符合题意;
∵AB=DC,AD=BC,
∴四边形ABCD是平行四边形,
故选项B不符合题意;
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
故选项C不符合题意;
∵AB∥DC,AD=BC,
∴四边形ABCD不一定是平行四边形,也可能是等腰梯形,故选项D符合题意,
2.C
解:过点作于,于.
两张长方形直尺的宽度相等,
,
又平行四边形的面积,
,
平行四边形为菱形.故②正确
当时,这个四边形是正方形,故①正确,③不正确
这个四边形一定是轴对称图形,故④正确
3.B
解:四边形和均为正方形,
,
.
四边形的周长
.
因为知道正方形和的面积,
所以它们的边长和对角线均可确定,
即与确定,一定能求出四边形的周长,其他选项不符合;
4.B
根据作图可知DE为的角平分线,即,
∵四边形ABCD为平行四边形,
∴,
∴,
∴,
∴,
∴,
∴在中,.
5.C
解:的周长为20,
,则.
四边形是平行四边形,对角线,相交于点,,
.
点是的中点,
是的中位线,,
,
的周长,
即的周长为8.
6.C
解:∵四边形ABCD是矩形
∴∠A=∠C=90°,AB=6,AD=8
∴
当为直角三角形时,有两种情况:
①当点在矩形内部时,如图1所示,
由折叠的性质得,,
设,则,
∴
在Rt中,
∴
解得,x=3
∴AE=3;
②当点落在边BC上时,如图2所示,
此时四边形是正方形,
∴AE=AB=6
7.D
解:如图延长交的延长线于,取的中点,连接.
∵,
∴,
∵是的中点,
∴,
∴,
∴,
∵,
∴,
∴,故A正确,
∵,
∴,
∵,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,故B正确,
∵,
∴
,故C正确,
∵,,,
∴,
∵,
∴四边形是平行四边形,
∵,
∴四边形是菱形,
∴,
∵,,,
∴,
∴,
∴,故D错误,
8.B
解:如图,
当点F与点C重合时,点P在P1处,CP1=DP1,
当点F与点E重合时,点P在P2处,EP2=DP2,
∴P1P2∥CE且P1P2=CE.
且当点F在EC上除点C、E的位置处时,有DP=FP.
由中位线定理可知:P1P∥CE且P1P=CF,
∴点P的运动轨迹是线段P1P2,
.∴当BP⊥P1P2时,PB取得最小值.
∵矩形ABCD中,AB:AD=2:1,设AB=2t,则AD=t,
∵E为AB的中点,
∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=t,
∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.
∴∠DP2P1=90°.
∴∠DP1P2=45°.
∴∠P2P1B=90°,即BP1⊥P1P2,
∴BP的最小值为BP1的长.
在等腰直角△BCP1中,CP1=BC=t,
∴BP1=t=,
∴t=3.
9.D
解:由矩形ABCD,得∠B=∠C=90°,CD=AB,AD=BC,AD∥BC.
由△DEC沿线段DE翻折,点C恰好落在线段AE上的点F处,得△DFE≌△DCE,
∴DF=DC,∠DFE=∠C=90°,
∴DF=AB,∠AFD=90°,
∴∠AFD=∠B,
由AD∥BC得∠DAF=∠AEB,
在△ABE与△DFA中,
,
∴△ABE≌△DFA(AAS).
∵BE:CE=4:1,
∴设CE=x,BE=4x,则AD=BC=5x,
由△ABE≌△DFA,得AF=BE=4x,
在Rt△ADF中,由勾股定理可得DF=3x,
又∵DF=CD=AB=6,
∴x=2,
在Rt△DCE中,DE===2.
10.D
解:∵HJ:JK:KF=2:1:2,
∴设HJ=2x,JK=x,KF=2x,
由折叠的性质得:AH=HJ=2x,
DH
=HK=3x,AE=EJ=
BE,
∴FH=5x,
∴AH:HD=2:3,
故D说法正确;
11.C
解:连接DE,
∵FG=且F、G分别为AD、AE中点,
∴DE=2FG=5,
∵四边形ABCD为矩形,
∴CD=AB=4,
在△CDE中,CE==3,
∵AE平分∠BAD,四边形ABCD为矩形,
∴∠BAD=∠ABE=90°,
∴∠BAE=∠BAD=45°,
在△ABE中,∠AEB=90°﹣∠AEB=45°,
∴∠BAE=∠AEB=45°,
△ABE为等腰直角三角形,
∴BE=AB=4,
又∵CE=3,
∴BC=BE+CE=4+3=7.
12.D
解:如图所示,过作于,过作于,
平行四边形中,,,
,,
又,
中,,
中,,
,
,
,,
,
又,
,
13.
如图所示:过点F作FN⊥BC交BC于点N,
设BE=xcm,则AE=BC=18-x,
在Rt△ABE中,,即
,
解得x=5,
∴AE=,
在矩形纸片中,则AE//MF,AD//BC,AB=AM,
∴∠AEB=∠FAE=∠AFM,
在△ABE和△AMF中
,
∴△ABE≌△AMF(AAS),
∴AF=AE=13cm,
∴DF=AD-AF=5,
∴EN=BC-BE-CN=BC-BE-DF=8,
在Rt△ENF中,EF=
.
14.3
解:如图,延长交于点,
四边形是平行四边形,
,,,
,,
,,
,
是等边三角形,为的中点,
,,
,
,
在和中,
,
,
,,
,,
,,
,,
是等边三角形,
,
,
15.
解:连接DE,如图,
由折叠可得,EF=BE,∠AFE=90°,∠AED=∠CED,
∵矩形ABCD,
∴BC=AD,∠BAF=∠B=90°,AD∥BC,
∴∠BAF=∠B=∠AFE=90°,∠ADE=∠DEC,
∴四边形ABEF为正方形,∠ADE=∠AED,
∴AB=BE=EF=AF,AD=AE,
设AB=a,则BC=AD=AE=a,
∴,
16.16
解:如图,连接BD交AC于点O,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC,
∵AE=CF=2,
∴OA-AE=OC-CF,即OE=OF,
∴四边形BEDF为平行四边形,且BD⊥EF,
∴四边形BEDF为菱形,
∴DE=DF=BE=BF,
∵AC=BD=8,OE=OF=,
∴EF=4,
∴四边形BEDF的面积为EF·BD==16,
17.15°
解:∵是等边三角形,
∴AM=AB=BM,∠MAB=60°,
∵四边形ABCD为正方形,
∴AD=AB,∠ADC=∠DAB=90°,
∴AM=AD,∠DAM=90°-∠MAB=90°-60°=30°,
∴∠ADM=∠AMD=,
∴∠MDC=∠ADC-∠ADM=90°-75°=15°.
18.1+
取AB的中点F,连接DF,
∠DCB=60°,BC=BD,
∠ADC=150°,AB=2,
以为边作等边,如图,连接,
则
为中点,
,
当且仅当过时,最长
此时.
19.8.5
解:连接FH,在菱形和菱形中,,
,
,
,
和同底等高,
菱形的面积为,,
,
,
20.4.8s或8s或9.6s
解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C-B,方程为12-4t=12-t,
此时方程t=0,此时不符合题意;
②点Q的运动路线是C-B-C,方程为4t-12=12-t,
解得:t=4.8;
③点Q的运动路线是C-B-C-B,方程为12-(4t-24)=12-t,
解得:t=8;
④点Q的运动路线是C-B-C-B-C,方程为4t-36=12-t,
解得:t=9.6;
综上所述,t=4.8s或8s或9.6s时,以P、D、Q、B四点组成的四边形为平行四边形,
21.见解析
证明:∵四边形ABCD是矩形,对角线AC,BD相交于点O,
∴OA=OC=OB=OD,
∵AE⊥BD,DF⊥AC,
∴∠AEO=∠DFO=90°,
在△AOE和△DOF中,
,
∴△AOE≌△DOF(AAS),
∴AE=DF.
22.(1)见解析;(2)△ABE,△ADE,△BCF,△DCE
证明:(1)∵四边形ABCD是平行四边形,
∴AD=BC,ADBC,
∴∠ADE=∠CBD,
∵AE⊥AD,CF⊥BC,
∴∠EAD=∠BCF=90°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
∴CF=AE,DE=BF,∠AEF=∠CFE,
∴AECF,
∴四边形AECF是平行四边形;
(2)∵点F为DE中点,
∴DF=EF,
∵BF=DE,
∴BE=DF=EF,
∴与四边形AECF面积相等有△ABF,△ADE,△BCF,△DCE.
23.(1)见解析;(2)
解:(1)∵BE∥AC,EC∥BD,
∴四边形BOCE是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠BOC=90°.
∴四边形BOCE是矩形.
(2)∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形.
∵四边形BOCE是矩形,
∴BF=BC=AB=1.
∴∠AFB=90°.
∴AF=.
24.(1)见解析;(2)
解:(1)∵四边形是平行四边形,
∴.
∵,
∴.
∴四边形是矩形.
(2)延长交于点G.
∵四边形是矩形,
∴,.
∴.
∵E是边的中点即,
∴.
∴.
∴.
∵,
∴.
∵,
∴.
∴.
设,由勾股定理得,
即:.解得.
25.(1)见解析;(2)52
解:(1)证明:∵AD∥BC,
∴∠DMO=∠BNO,
∵MN是对角线BD的垂直平分线,
∴OB=OD,MN⊥BD,
在△MOD和△NOB中,
,
∴△MOD≌△NOB(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BNDM是平行四边形,
∵MN⊥BD,
∴四边形BNDM是菱形;
(2)∵BD=24,菱形BNDM的面积为120,
∴MN=120×2÷24=10,
∴BM=BN=DM=DN,OB=BD=12,OM=MN=5,
在Rt△BOM中,由勾股定理得:BM==13,
∴菱形BNDM的周长=4BM=4×13=52.
26.(1)见解析;(2)①,证明见解析;②
解:(1)如图所示,
四边形是正方形,是对角线,
,
,
是等腰直角三角形,
;
(2)①如图所示,连接、,
是等腰直角三角形,
,,
,
又,
,
,
,
,
,
,,
,
是等腰直角三角形,
,
即;
②,理由如下:
如图,连接,
,
,
又且,
,,
四边形是平行四边形,
,
,,
,
又,,
,
则.
27.(1)见解析;(2)45°
(1)证明:在正方形中,
∵,,,
∴.
∴.
(2)解:∵,
∴.
∵,,
∴.
∴,
∵,
又∵,
∴.
