2021—2022学年人教版数学九年级上册24.1.1圆同步练习(word解析版)
文档属性
| 名称 | 2021—2022学年人教版数学九年级上册24.1.1圆同步练习(word解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 231.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 12:29:06 | ||
图片预览



文档简介
24.1.1 圆
知识点
1 与圆有关的概念
1.自行车车轮要做成圆形,实际上是根据圆的特征
( )
A.圆是轴对称图形
B.直径是圆中最长的弦
C.圆上各点到圆心的距离相等
D.圆是中心对称图形
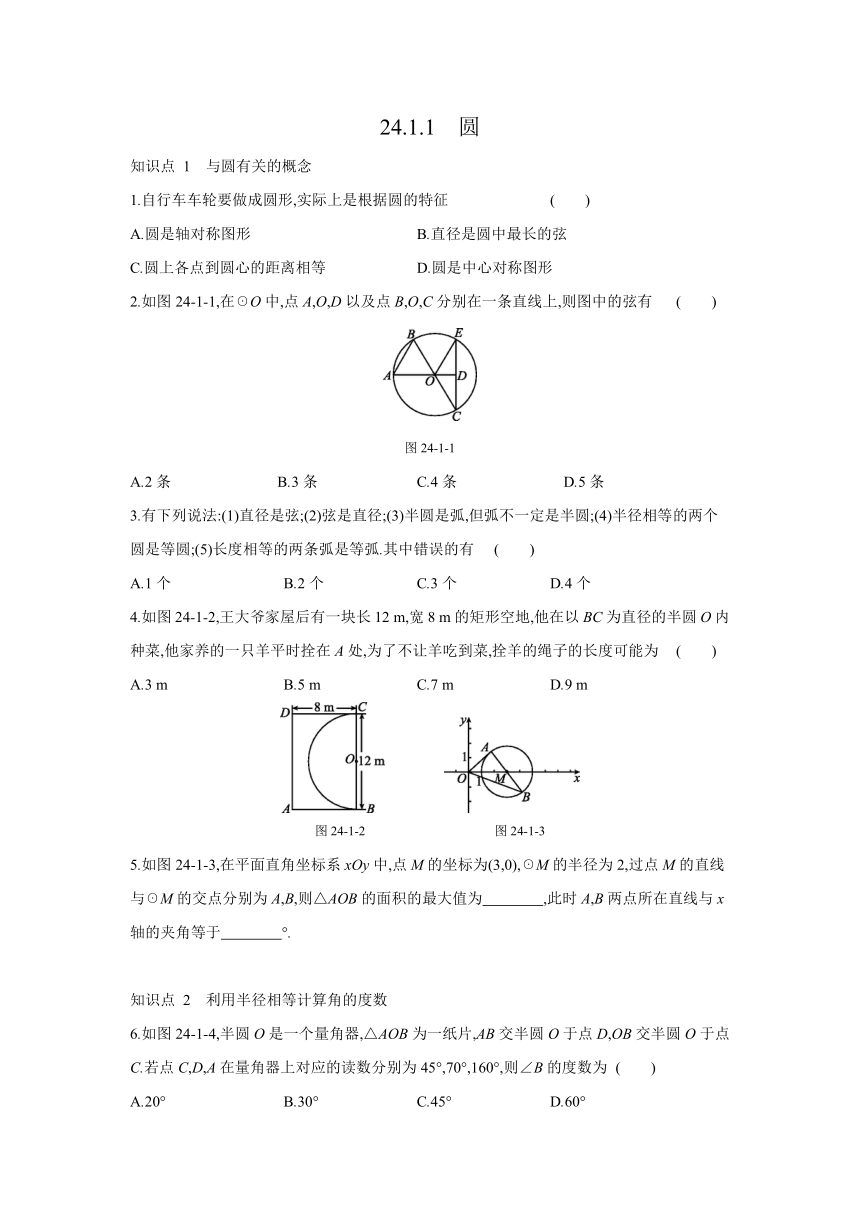
2.如图24-1-1,在☉O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有
( )
图24-1-1
A.2条 B.3条
C.4条 D.5条
3.有下列说法:(1)直径是弦;(2)弦是直径;(3)半圆是弧,但弧不一定是半圆;(4)半径相等的两个圆是等圆;(5)长度相等的两条弧是等弧.其中错误的有
( )
A.1个
B.2个
C.3个
D.4个
4.如图24-1-2,王大爷家屋后有一块长12
m,宽8
m的矩形空地,他在以BC为直径的半圆O内种菜,他家养的一只羊平时拴在A处,为了不让羊吃到菜,拴羊的绳子的长度可能为
( )
A.3
m
B.5
m
C.7
m
D.9
m
图24-1-2
图24-1-3
5.如图24-1-3,在平面直角坐标系xOy中,点M的坐标为(3,0),☉M的半径为2,过点M的直线与☉M的交点分别为A,B,则△AOB的面积的最大值为 ,此时A,B两点所在直线与x轴的夹角等于 °.?
知识点
2 利用半径相等计算角的度数
6.如图24-1-4,半圆O是一个量角器,△AOB为一纸片,AB交半圆O于点D,OB交半圆O于点C.若点C,D,A在量角器上对应的读数分别为45°,70°,160°,则∠B的度数为
( )
A.20°
B.30°
C.45°
D.60°
图24-1-4
图24-1-5
7.如图24-1-5,以△ABC的边BC为直径的☉O分别交AB,AC于点D,E,连接OD,OE.若∠A=65°,则∠DOE= °.?
8.如图24-1-6,直线AB经过☉O的圆心,与☉O相交于点A,B,点C在☉O上,且∠AOC=30°,P是直线AB上的一个动点(与点O不重合),直线PC与☉O相交于点Q.在直线AB上使QP=QO成立的点P共有几个?请相应地求出∠OCP的度数.
图24-1-6
知识点
3 利用半径相等计算线段的长度
9.如图24-1-7,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是
( )
A.猫先到达B地
B.老鼠先到达B地
C.猫和老鼠同时到达B地
D.无法确定
图24-1-7
图24-1-8
10.如图24-1-8,OA是☉O的半径,B为OA上一点(不与点O,A重合),过点B作OA的垂线交☉O于点C.以OB,BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为
( )
A.8
B.6
C.4
D.2
11.如图24-1-9,两个正方形彼此相邻且内接于半圆.若小正方形的面积为16
cm2,求该半圆的半径.
图24-1-9
知识点
4 利用半径相等进行证明
12.如图24-1-10,AB,CD为☉O的两条直径,M,N分别为OA,OB的中点.
(1)求证:四边形CMDN为平行四边形;
(2)四边形CMDN能是菱形吗?若能,请你直接写出需要添加的条件.
图24-1-10
知识点
5 证明四点共圆
13.如图24-1-11所示,若BD,CE都是△ABC的高,求证:B,C,D,E四点在同一个圆上.
图24-1-11
能力拓展提升
14.如图24-1-12,在平面直角坐标系中,动点P在以点O为圆心,10为半径的圆上运动,则横、纵坐标都是整数的点P有 个.?
图24-1-12
典题讲评与答案详析
1.C [解析]
车轮做成圆形是为了在行进过程中保持和地面的高度不变,是利用了圆上各点到圆心的距离相等.故选C.
2.B 3.B
4.A [解析]
如图,连接OA交半圆O于点P,不让羊吃到菜,就是说羊的活动范围最多只能在以A为圆心,AP为半径的圆内(不包括边界).由题意得,OB=OP=6,AB=8,则OA==10,所以AP=OA-OP=10-6=4.所以,为了不让羊吃到菜,拴羊的绳子的长度应小于4
m.故选A.
5.6 90 [解析]
∵AB为☉M的直径,∴AB=4.
当点O到AB的距离最大时,△AOB的面积最大,此时AB⊥x轴于点M,
∴△AOB的面积的最大值为×4×3=6,∠AMO=90°.
即此时A,B两点所在直线与x轴的夹角等于90°.
6.A [解析]
连接OD,如图,则∠DOC=70°-45°=25°,∠AOD=160°-70°=90°.
∵OD=OA,∴∠ADO=45°.
∵∠ADO=∠B+∠DOB,
∴∠B=45°-25°=20°.
故选A.
7.50 [解析]
由三角形的内角和定理,得∠B+∠C=180°-∠A.由OB=OD=OC=OE,得到
∠BDO=∠B,∠CEO=∠C.在等腰三角形BOD和等腰三角形COE中,∠DOB+∠EOC=180°-
2∠B+180°-2∠C=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以∠DOE=180°-2∠A=50°.
8.解:在直线AB上使QP=QO成立的点P共有3个.
(1)如图①.
在△QOC中,∵OC=OQ,∴∠OQC=∠OCQ.
在△OPQ中,∵QP=QO,∴∠QOP=∠QPO.
又∵∠QPO=∠OCQ+∠AOC,且∠AOC=30°,∠QOP+∠QPO+∠OQC=180°,
∴3∠OCQ=120°,∴∠OCQ=40°,
即∠OCP=40°.
(2)如图②.
∵QO=QP,∴∠QPO=∠QOP.
设∠QPO=x,则∠OQC=∠QPO+∠QOP=2x.又∵OC=OQ,∴∠OCQ=∠OQC=2x,
∴∠AOC=∠OPC+∠OCP=x+2x=3x.
∵∠AOC=30°,∴3x=30°,解得x=10°,
∴∠OCP=2x=20°.
(3)如图③.
∵QO=QP,∴∠QOP=∠QPO.
∵OC=OQ,∴∠OQC=∠OCQ.
设∠QPO=y,则∠OQC=∠OCQ=∠QPO+∠AOC=y+30°,
∴在△OPQ中,有y+y+y+30°=180°,
解得y=50°,
∴∠OCP=180°-50°-30°=100°.
综上所述,在直线AB上使QP=QO成立的点P共有3个,∠OCP的度数分别为40°,20°,100°.
9.C 10.C
11.解:如图,连接OA,OB.
根据正方形的面积公式可得小正方形的边长为4
cm.
设大正方形的边长为x
cm,则OD=x
cm.
根据勾股定理,得OA2=OD2+AD2,OB2=OC2+BC2.
又∵OA=OB,
∴x2+x2=x+42+42,
解得x1=8,x2=-4(不符合题意,舍去),
∴大正方形的边长为8
cm,OD=4
cm,
∴OA2=OD2+AD2=42+82=80,
∴OA==4(cm).
故该半圆的半径为4
cm.
12.解:(1)证明:∵M,N分别为OA,OB的中点,
∴OM=OA,ON=OB.
又∵OA=OB,∴OM=ON.
又∵OC=OD,
∴四边形CMDN为平行四边形.
(2)四边形CMDN能是菱形.
需要添加条件:CD⊥AB.
13.证明:取BC的中点F,连接DF,EF.
∵BD,CE都是△ABC的高,
∴△BCD和△BCE都是直角三角形,
∴DF,EF分别是Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF,
∴B,C,D,E四点都在以点F为圆心,BF的长为半径的圆上,即B,C,D,E四点在同一个圆上.
14.12 [解析]
设点P(x,y).
由题意,知x2+y2=102=100,
则方程的整数解是:x=6,y=8;x=8,y=6;x=10,y=0;x=6,y=-8;x=8,y=-6;x=0,y=-10;
x=-6,y=-8;x=-8,y=-6;x=-10,y=0;x=-6,y=8;x=-8,y=6;x=0,y=10.
所以点P的坐标可以是(6,8),(8,6),(10,0),(6,-8),(8,-6),(0,-10),(-6,-8),(-8,-6),(-10,0),(-6,8),(-8,6),(0,10),
所以横、纵坐标都是整数的点P有12个.
知识点
1 与圆有关的概念
1.自行车车轮要做成圆形,实际上是根据圆的特征
( )
A.圆是轴对称图形
B.直径是圆中最长的弦
C.圆上各点到圆心的距离相等
D.圆是中心对称图形
2.如图24-1-1,在☉O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有
( )
图24-1-1
A.2条 B.3条
C.4条 D.5条
3.有下列说法:(1)直径是弦;(2)弦是直径;(3)半圆是弧,但弧不一定是半圆;(4)半径相等的两个圆是等圆;(5)长度相等的两条弧是等弧.其中错误的有
( )
A.1个
B.2个
C.3个
D.4个
4.如图24-1-2,王大爷家屋后有一块长12
m,宽8
m的矩形空地,他在以BC为直径的半圆O内种菜,他家养的一只羊平时拴在A处,为了不让羊吃到菜,拴羊的绳子的长度可能为
( )
A.3
m
B.5
m
C.7
m
D.9
m
图24-1-2
图24-1-3
5.如图24-1-3,在平面直角坐标系xOy中,点M的坐标为(3,0),☉M的半径为2,过点M的直线与☉M的交点分别为A,B,则△AOB的面积的最大值为 ,此时A,B两点所在直线与x轴的夹角等于 °.?
知识点
2 利用半径相等计算角的度数
6.如图24-1-4,半圆O是一个量角器,△AOB为一纸片,AB交半圆O于点D,OB交半圆O于点C.若点C,D,A在量角器上对应的读数分别为45°,70°,160°,则∠B的度数为
( )
A.20°
B.30°
C.45°
D.60°
图24-1-4
图24-1-5
7.如图24-1-5,以△ABC的边BC为直径的☉O分别交AB,AC于点D,E,连接OD,OE.若∠A=65°,则∠DOE= °.?
8.如图24-1-6,直线AB经过☉O的圆心,与☉O相交于点A,B,点C在☉O上,且∠AOC=30°,P是直线AB上的一个动点(与点O不重合),直线PC与☉O相交于点Q.在直线AB上使QP=QO成立的点P共有几个?请相应地求出∠OCP的度数.
图24-1-6
知识点
3 利用半径相等计算线段的长度
9.如图24-1-7,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是
( )
A.猫先到达B地
B.老鼠先到达B地
C.猫和老鼠同时到达B地
D.无法确定
图24-1-7
图24-1-8
10.如图24-1-8,OA是☉O的半径,B为OA上一点(不与点O,A重合),过点B作OA的垂线交☉O于点C.以OB,BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为
( )
A.8
B.6
C.4
D.2
11.如图24-1-9,两个正方形彼此相邻且内接于半圆.若小正方形的面积为16
cm2,求该半圆的半径.
图24-1-9
知识点
4 利用半径相等进行证明
12.如图24-1-10,AB,CD为☉O的两条直径,M,N分别为OA,OB的中点.
(1)求证:四边形CMDN为平行四边形;
(2)四边形CMDN能是菱形吗?若能,请你直接写出需要添加的条件.
图24-1-10
知识点
5 证明四点共圆
13.如图24-1-11所示,若BD,CE都是△ABC的高,求证:B,C,D,E四点在同一个圆上.
图24-1-11
能力拓展提升
14.如图24-1-12,在平面直角坐标系中,动点P在以点O为圆心,10为半径的圆上运动,则横、纵坐标都是整数的点P有 个.?
图24-1-12
典题讲评与答案详析
1.C [解析]
车轮做成圆形是为了在行进过程中保持和地面的高度不变,是利用了圆上各点到圆心的距离相等.故选C.
2.B 3.B
4.A [解析]
如图,连接OA交半圆O于点P,不让羊吃到菜,就是说羊的活动范围最多只能在以A为圆心,AP为半径的圆内(不包括边界).由题意得,OB=OP=6,AB=8,则OA==10,所以AP=OA-OP=10-6=4.所以,为了不让羊吃到菜,拴羊的绳子的长度应小于4
m.故选A.
5.6 90 [解析]
∵AB为☉M的直径,∴AB=4.
当点O到AB的距离最大时,△AOB的面积最大,此时AB⊥x轴于点M,
∴△AOB的面积的最大值为×4×3=6,∠AMO=90°.
即此时A,B两点所在直线与x轴的夹角等于90°.
6.A [解析]
连接OD,如图,则∠DOC=70°-45°=25°,∠AOD=160°-70°=90°.
∵OD=OA,∴∠ADO=45°.
∵∠ADO=∠B+∠DOB,
∴∠B=45°-25°=20°.
故选A.
7.50 [解析]
由三角形的内角和定理,得∠B+∠C=180°-∠A.由OB=OD=OC=OE,得到
∠BDO=∠B,∠CEO=∠C.在等腰三角形BOD和等腰三角形COE中,∠DOB+∠EOC=180°-
2∠B+180°-2∠C=360°-2(∠B+∠C)=360°-2(180°-∠A)=2∠A,所以∠DOE=180°-2∠A=50°.
8.解:在直线AB上使QP=QO成立的点P共有3个.
(1)如图①.
在△QOC中,∵OC=OQ,∴∠OQC=∠OCQ.
在△OPQ中,∵QP=QO,∴∠QOP=∠QPO.
又∵∠QPO=∠OCQ+∠AOC,且∠AOC=30°,∠QOP+∠QPO+∠OQC=180°,
∴3∠OCQ=120°,∴∠OCQ=40°,
即∠OCP=40°.
(2)如图②.
∵QO=QP,∴∠QPO=∠QOP.
设∠QPO=x,则∠OQC=∠QPO+∠QOP=2x.又∵OC=OQ,∴∠OCQ=∠OQC=2x,
∴∠AOC=∠OPC+∠OCP=x+2x=3x.
∵∠AOC=30°,∴3x=30°,解得x=10°,
∴∠OCP=2x=20°.
(3)如图③.
∵QO=QP,∴∠QOP=∠QPO.
∵OC=OQ,∴∠OQC=∠OCQ.
设∠QPO=y,则∠OQC=∠OCQ=∠QPO+∠AOC=y+30°,
∴在△OPQ中,有y+y+y+30°=180°,
解得y=50°,
∴∠OCP=180°-50°-30°=100°.
综上所述,在直线AB上使QP=QO成立的点P共有3个,∠OCP的度数分别为40°,20°,100°.
9.C 10.C
11.解:如图,连接OA,OB.
根据正方形的面积公式可得小正方形的边长为4
cm.
设大正方形的边长为x
cm,则OD=x
cm.
根据勾股定理,得OA2=OD2+AD2,OB2=OC2+BC2.
又∵OA=OB,
∴x2+x2=x+42+42,
解得x1=8,x2=-4(不符合题意,舍去),
∴大正方形的边长为8
cm,OD=4
cm,
∴OA2=OD2+AD2=42+82=80,
∴OA==4(cm).
故该半圆的半径为4
cm.
12.解:(1)证明:∵M,N分别为OA,OB的中点,
∴OM=OA,ON=OB.
又∵OA=OB,∴OM=ON.
又∵OC=OD,
∴四边形CMDN为平行四边形.
(2)四边形CMDN能是菱形.
需要添加条件:CD⊥AB.
13.证明:取BC的中点F,连接DF,EF.
∵BD,CE都是△ABC的高,
∴△BCD和△BCE都是直角三角形,
∴DF,EF分别是Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF,
∴B,C,D,E四点都在以点F为圆心,BF的长为半径的圆上,即B,C,D,E四点在同一个圆上.
14.12 [解析]
设点P(x,y).
由题意,知x2+y2=102=100,
则方程的整数解是:x=6,y=8;x=8,y=6;x=10,y=0;x=6,y=-8;x=8,y=-6;x=0,y=-10;
x=-6,y=-8;x=-8,y=-6;x=-10,y=0;x=-6,y=8;x=-8,y=6;x=0,y=10.
所以点P的坐标可以是(6,8),(8,6),(10,0),(6,-8),(8,-6),(0,-10),(-6,-8),(-8,-6),(-10,0),(-6,8),(-8,6),(0,10),
所以横、纵坐标都是整数的点P有12个.
同课章节目录
